绝对值不等式一元二次不等的解法测试题

不等式练习题一、基本不等式1. 已知a > b，求证：a + c > b + c。

2. 已知x > 3，求证：x^2 > 9。

3. 已知0 < x < 1，求证：x^3 < x。

4. 已知a, b均为正数，求证：a^2 + b^2 > 2ab。

5. 已知|x| > |y|，求证：x^2 > y^2。

二、一元一次不等式1. 解不等式：3x 7 > 2x + 4。

2. 解不等式：5 2(x 3) ≤ 3x 1。

3. 解不等式：2(x 1) 3(x + 2) > 7。

4. 解不等式：4 3(x 2) ≥ 2x + 5。

5. 解不等式：5(x 3) + 2(2x + 1) < 7x 9。

三、一元二次不等式1. 解不等式：x^2 5x + 6 > 0。

2. 解不等式：2x^2 3x 2 < 0。

3. 解不等式：x^2 4x + 4 ≤ 0。

4. 解不等式：3x^2 + 4x 4 > 0。

5. 解不等式：x^2 + 5x 6 < 0。

四、分式不等式1. 解不等式：x / (x 1) > 2。

2. 解不等式：1 / (x + 3) 1 / (x 2) ≤ 0。

3. 解不等式：(x 1) / (x + 1) < 0。

4. 解不等式：(2x + 3) / (x 4) ≥ 1。

5. 解不等式：(3x 2) / (x^2 5x + 6) > 0。

五、含绝对值的不等式1. 解不等式：|x 2| > 3。

2. 解不等式：|2x + 1| ≤ 5。

3. 解不等式：|3x 4| < 2。

4. 解不等式：|x + 3| |x 2| > 1。

5. 解不等式：|x 5| + |x + 1| < 6。

六、综合应用题1. 已知不等式组：$\begin{cases} 2x 3y > 6 \\ x + 4y ≤ 8 \end{cases}$，求x的取值范围。

高三数学一元二次不等式试题答案及解析1.如果命题“关于的不等式的解集是空集”是假命题，则实数的取值范围是_______.【答案】【解析】由已知，有解，所以，解得实数的取值范围是.【考点】命题，一元二次不等式的解法.2.已知函数则满足的实数的取值范围是 .【答案】【解析】或，∴或，∴.【考点】不等式的解法.3.不等式≤x－2的解集是()A．(－∞，0]∪(2,4]B．[0,2)∪[4，＋∞)C．[2,4)D．(－∞，2]∪(4，＋∞)【答案】B【解析】①当x－2>0，即x>2时，不等式可化为(x－2)2≥4，∴x≥4；②当x－2<0，即x<2时，不等式可化为(x－2)2≤4，∴0≤x<2.4.已知二次函数f(x)＝ax2－(a＋2)x＋1(a∈Z)，且函数f(x)在(－2，－1)上恰有一个零点，则不等式f(x)>1的解集为()A．(－∞，－1)∪(0，＋∞)B．(－∞，0)∪(1，＋∞)C．(－1,0)D．(0,1)【答案】C【解析】∵f(x)＝ax2－(a＋2)x＋1，Δ＝(a＋2)2－4a＝a2＋4>0，∴函数f(x)＝ax2－(a＋2)x＋1必有两个不同的零点．因此f(－2)f(－1)<0，∴(6a＋5)(2a＋3)<0.∵－<a<－.又a∈Z，∴a＝－1，不等式f(x)>1即为－x2－x>0，解得－1<x<0.故选C.5.设二次函数f(x)＝ax2＋bx＋c，函数F(x)＝f(x)－x的两个零点为m，n(m<n)．(1)若m＝－1，n＝2，求不等式F(x)>0的解集；(2)若a>0，且0<x<m<n<，比较f(x)与m的大小．【答案】（1）当a>0时，不等式F(x)>0的解集为{x|x<－1或x>2}；当a<0时，不等式F(x)>0的解集为{x|－1<x<2}．（2）f(x)<m.【解析】解：(1)由题意知，F(x)＝f(x)－x＝a(x－m)(x－n)，当m＝－1，n＝2时，不等式F(x)>0，即a(x＋1)(x－2)>0.当a>0时，不等式F(x)>0的解集为{x|x<－1或x>2}；当a<0时，不等式F(x)>0的解集为{x|－1<x<2}．(2)f(x)－m＝F(x)＋x－m＝a(x－m)(x－n)＋x－m＝(x－m)(ax－an＋1)，∵a>0，且0<x<m<n<，∴x－m<0,1－an＋ax>0.∴f(x)－m<0，即f(x)<m.6.对于满足0≤a≤4的实数a，使x2＋ax>4x＋a－3恒成立的x取值范围是________．【答案】(－∞，－1)∪(3，＋∞)【解析】原不等式等价于x2＋ax－4x－a＋3>0，∴a(x－1)＋x2－4x＋3>0，令f(a)＝a(x－1)＋x2－4x＋3，则函数f(a)＝a(x－1)＋x2－4x＋3表示直线，∴要使f(a)＝a(x－1)＋x2－4x＋3>0，则有f(0)>0，f(4)>0，即x2－4x＋3>0且x2－1>0，解得x>3或x<－1，即不等式的解集为(－∞，－1)∪(3，＋∞)．7.（2013•重庆）设0≤α≤π，不等式8x2﹣（8sinα）x+cos2α≥0对x∈R恒成立，则α的取值范围为_________．【答案】[0，]∪[，π]【解析】由题意可得，△=64sin2α﹣32cos2α≤0，得2sin2α﹣（1﹣2sin2α）≤0∴sin2α≤，﹣≤sinα≤，∵0≤α≤π∴α∈[0，]∪[，π]8.若不等式|8x＋9|<7和不等式ax2＋bx>2的解集相等，则实数a、b的值分别为()A．a＝－8，b＝－10B．a＝－4，b＝－9C．a＝－1，b＝9D．a＝－1，b＝2【答案】B【解析】根据题意可得|8x＋9|<7⇒－2<x<，故由{x|－2<x<}是不等式ax2＋bx>2的解集可知x1＝－2，x2＝是一元二次方程ax2＋bx－2＝0的两根，根据根与系数的关系可知x1x2＝＝⇒a＝－4，x1＋x2＝＝⇒b＝－9，故选B.9.不等式3x2－x－4≤0的解集是__________.【答案】【解析】由3x2－x－4≤0，得(3x－4)(x＋1)≤0，解得－1≤x≤.10.已知f(x)是定义域为R的偶函数，当x≥0时，f(x)＝x2－4x，那么不等式f(x＋2)<5的解集是________．【答案】(－7，3)【解析】解f(x)＝x2－4x<5(x≥0)，得0≤x<5.由f(x)是定义域为R的偶函数得不等式f(x)<5的解集是(－5，5)，所以不等式f(x＋2)<5转化为－5<x＋2<5，故所求的解集是(－7，3)．11.不等式x2-5x+6≤0的解集为.【答案】{x|2≤x≤3}【解析】x2-5x+6≤0,即(x-2)(x-3)≤0,故2≤x≤3.12.设f(x)=x2-bx+c,不等式f(x)<0的解集是(-1,3),若f(7+|t|)>f(1+t2),求实数t的取值范围.【答案】-3<t<3【解析】∵x2-bx+c<0的解集是(-1,3),∴>0且-1,3是x2-bx+c=0的两根,∴得∵函数f(x)=x2-bx+c图象的对称轴方程为x==1,且f(x)在[1,+∞)上是增函数,又∵7+|t|≥7>1,1+t2≥1,则由f(7+|t|)>f(1+t2),得7+|t|>1+t2,即|t|2-|t|-6<0,亦即(|t|+2)(|t|-3)<0,∴|t|<3,即-3<t<3.13.不等式(x－1)·≥0的解集为________．【答案】{x|x≥2或x＝－1}【解析】原不等式等价于(x－1)>0①或(x－1)·＝0②，解①，由得x>2；解②，由x2－x－2＝0或x－1＝0且有意义，得x＝－1或x＝2.综上可知，原不等式的解集是{x|x≥2或x＝－1}．14.已知x＞0，y＞0，若恒成立，则实数m的取值范围是（）A．m≥4或m≤－2B．m≥2或m≤－4C．－2＜m＜4D．－4＜m＜2【答案】D【解析】因为，要使恒成立，则，解得－4＜m＜2，选D.【考点】基本不等式、一元二次不等式的解法.15.己知函数.(I)若关于的不等式的解集不是空集，求实数的取值范围；(II)若关于的一元二次方程有实根，求实数的取值范围.【答案】(I)；(II)【解析】(I)由题意知，只需，解出即可，根据绝对值不等式的性质知，故，解得或；(II)由题意方程有实根，则，即，化简得，提出得，，根据绝对值的几何意义知，此式表示的是到的距离与到的距离之和小于，从数轴上易知.试题解析：(I)由题意，，，解得或，所以的取值范围为.(II)由题意，，化简得，即，所以，故的取值范围为.【考点】1.绝对值不等式的解法；2.一元二次方程根的判断.16.已知不等式的解集为，则不等式的解集为（）A．B．C．D．【答案】D【解析】由已知得且2，4为一元二次方程两根，由韦达定理得①，②．①除以②，得由②得注意到不等式或．故选D．【考点】一元二次不等式的解法．17.设与是定义在同一区间上的两个函数，若对任意的，都有，则称和在上是“密切函数”，称为“密切区间”，设与在上是“密切函数”，则它的“密切区间”可以是（）A．B．C．D．【答案】D【解析】由题意由，得，解之得，故选D.【考点】1.含绝对值的一元二次不等式的解法；2.函数新定义题18.设集合，，则（）A．B．C．D．【答案】B【解析】.【考点】1.指数不等式的解法；2.一元二次不等式的解法；3.集合的运算.19.已知关于的一元二次不等式的解集中有且仅有3个整数，则所有符合条件的的值之和是（）A．13B．18C．21D．26【答案】C【解析】设，其图象是开口向上，对称轴是x=3的抛物线，如图所示．若关于的一元二次不等式的解集中有且仅有3个整数，则，即，解得，又则所有符合条件的的值之和是6+7+8=21．故选C．【考点】一元二次不等式解法，二次函数的图象和性质.20.已知不等式>0的解集为(-1，2)，是和的等比中项，那么=A．3B．-3C．-1D．1【答案】D【解析】根据题意，由于不等式>0的解集为(-1，2)，那么可知-1是因式ax+b=0的根，所以a=b,又因为是和的等比中项，则有，可知，故答案为1，选D.【考点】一元二次不等式的解集点评:解决的关键是对于等比中项以及二次不等式的解集的准确表示，属于基础题。

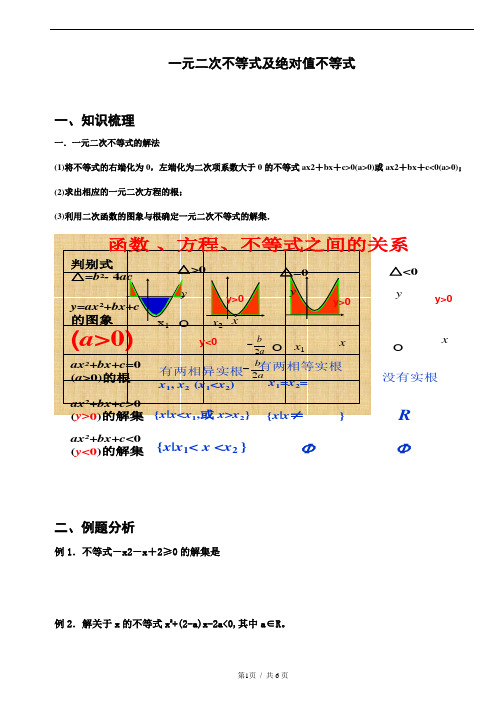
一元二次不等式及绝对值不等式一、知识梳理一．一元二次不等式的解法(1)将不等式的右端化为0，左端化为二次项系数大于0的不等式ax2＋bx＋c>0(a>0)或ax2＋bx＋c<0(a>0)；(2)求出相应的一元二次方程的根；(3)利用二次函数的图象与根确定一元二次不等式的解集．ax2+bx+c<0(y<0)的解集{x|x1< x <x2}△<0yxOΦΦR没有实根y>0二、例题分析例1．不等式－x2－x＋2≥0的解集是例2．解关于x的不等式x2+(2-a)x-2a<0,其中a∈R。

例3．已知关于x的不等式x2＋ax＋b<0的解集为(1,2)．试求关于x的不等式bx2＋ax＋1>0的解集．例4、-x+10 3x+1>变式1、-10 3+1xx+≥变式2.-x+12 3+1x≥二，|x|的几何意义是实数x在数轴上对应的点离开原点O的距离，所以|x|<a (a>0)的解集是{x|-a<x<a}；不等式|x|>a (a>0)的解集是{x|x>a或x<-a}。

把不等式|x|<a与|x|>a (a>0)中的x替换成ax+b，就可以得到|ax+b|<c与|ax+b|>c (c>0)型的不等式的解法。

例5．解关于x的不等式|3x-2|<4变式引深：解关于x的不等式|ax-2|<4，其中a∈R。

例6. 解不等式|x-3|-|2x+3|≥2。

变式：|x－1|<|x+7|例7、|2x－2x－6|<3x三、课后变式小提升1、8x－1≥16x22、2x2＋4x＋3>0；3、－3x2－2x＋8>0；4、解不等式1<|x-2|≤75、|x+1|>2－x6、2|55|1 x x-+<．7、解不等式｜x-2｜+｜x+3｜>5.8、解50 23xx+< -9、解530 23xx+>-10、解530 23xx+≥-11、解532 23xx+≥-四、课后作业：复习所讲内容，完成课后小练习，加油哦！！！。

含绝对值的不等式解法，一元二次不等式解法：|x|的几何意义是实数x在数轴上对应的点离开原点O的距离，所以|x|<a (a>0)的解集是{x|-a<x<a}；不等式|x|>a (a>0)的解集是{x|x>a或x<-a}把不等式|x|<a与|x|>a (a>0)中的x替换成ax+b可以得到|ax+b|<c与|ax+b|>c (c>0)型的不等式的解法。

一元二次不等式ax2+bx+c>0(或<0)的解可以联系二次函数y=ax2+bx+c的图象(a≠0)图象在x轴上方部分对应的x值为不等式ax2+bx+c>0的解，图象在x轴下方部分对应的x值为不等式ax2+bx+c<0的解。

而方程ax2+bx+c=0的根表示图象与x轴交点的横坐标。

求解一元二次不等式的步骤，先把二次项系数化为正数，再解对应的一元二次方程，最后根据一元二次方程的根，结合不等号的方向，写出不等式的解集。

x2+3x-4<0 (x+4)(x-1)<0 或或-4<x<1或。

原不等式解集为{x|-4<x<1}。

x2+3x-4<0 (x+)2<|x+|<-<x+<-4<x<1原不等式解集为{x|-4<x<1}。

例1．解关于x的不等式|ax-2|<4，其中a∈R。

解：|ax-2|<4属于|x|<c(c>0)型。

∴-4<ax-2<4, 不等号各端加2，得-2<ax<6。

当a>0时，-<x<，当a<0时，->x>, 当a=0时不等式化为2<4，显然x∈故a>0时不等式解集是{x|-<x<}，a<0时不等式解集是{x|<x<-}，a=0时不等式解集是R。

常见不等式的解法(教师版)一、一元一次不等式解下列关于x的不等式1、2x+3>52、-2x+5<63、ax>14、不等式3(x+1)≥5x-9的正整数解是5、已知关于x的不等式(3a-2)x+2<3的解集是,则a= .二、一元二次不等式1、2、3、x2+x-2≤4 4、若0＜a＜1，则不等式(x-a)(x-)＜0的解是 .a＜x＜5、已知不等式的解集为，则的值为 .-146、不等式2x2-3|x|-35>0的解为 ..x<-5或x>57、方程则实数m的取值范围是.8、不等式的解集是，则m= __，n= __.-1;-69、函数或10、对于任意实数x，一元二次不等式(2m-1)x2+(m+1)x+(m-4)＞0恒成立，则实数m的取值范围是 .m＞511、函数则a的取值范围是【0,8】二、分式不等式的解法1）标准化：移项通分化为(或)；(或)的形式，2）转化为整式不等式（组） 1. 不等式的解集是 2. 不等式的解集是3. 不等式的解集是4. 不等式的解集是5. 不等式的解集是6. 不等式的解集是7. 不等式的解集是8. 不等式的解集是9. 不等式的解集是10. 不等式的解集是答案1. 2. (-2，3)3. 4.9.10.三、无理不等式的解法无理不等式一般是指在根号下含有未知数的不等式，今天我们主要研究在二次根号下含有未知数的简单的无理不等式的解法。

题型Ⅰ：例一解不等式解：移项：∴∴不等式的解集是：{}练习一：解不等式⑴⑵解：⑴移项：∴∴∴原不等式的解集为⑵∴∴原不等式的解集为{}例二解不等式解：原不等式的解集等价于下面两个不等式组解集的并集：Ⅰ：或Ⅱ：解Ⅰ：解Ⅱ：即：或∴∴原不等式的解集为{}题型Ⅱ：练习二：解不等式解：原不等式的解集等价于下面两个不等式组解集的并集：Ⅰ：或Ⅱ：解Ⅰ：解Ⅱ：即：或∴∴原不等式的解集为{}四、含绝对值的不等式的解法(一)、公式法：即利用与的解集求解。

一元二次不等式的解法练习题（1）1. 不等式−2x 2+x +3≤0的解集是（ ）A. B.{x|x ≤−1或x ≥}C.{x|x ≤−或x ≥1}D.2. 不等式x 2−7x <0的解集是（ ） A.{x|x <−7或x >0} B.{x|x <0或x >7} C.{x|−7<x <0}D.{x|0<x <7}3. 不等式x 2+2x −3≥0的解集是( ) A.{x|x ≥1} B.{x|x ≤−3} C.{x|−3≤x ≤1} D.{x|x ≤−3或x ≥1}4. 不等式x 2−4x −5>0的解集为( )A.{x|x ≥5或x ≤−1}B.{x|x >5或x <−1}C.{x|−1≤x ≤5}D.{x|−1<x <5}5. 不等式2x 2−x −1>0的解集是（ ） A.(−12,1)B.(1,+∞)C.(−∞,1)∪(2,+∞)D.(−∞,−12)∪(1,+∞)6. 不等式组{x 2−2x −3<0log 2x <0 的解集为（ ）A.(−1, 0)B.(−1, 1)C.(0, 1)D.(1, 3)7. 已知集合A ＝{x ∈N|−2<x <4}，B ={x|12≤2x ≤4}，则A ∩B ＝（ ） A.{x|−1≤x ≤2} B.{−1, 0, 1, 2} C.{1, 2} D.{0, 1, 2}8. 下列四个不等式中，解集为⌀的是（）A.−x2+x+1≤0B.2x2−3x+4<0C.x2+6x+9≤0D.9. 已知函数f(x)＝3x2−6x−1，则（）A.函数f(x)有两个不同的零点B.函数f(x)在(−1, +∞)上单调递增C.当a>1时，若f(a x)在x∈[−1, 1]上的最大值为8，则a＝3D.当0<a<1时，若f(a x)在x∈[−1, 1]上的最大值为8，则a=1310. 已知集合A={−1,0,2}, B={2,a2}，若B⊆A，则实数a的值为________.11. 不等式|x−3|<2的解集为________．12. 不等式3x2−6x−5>4的解集为________.13. 已知不等式kx2−2x+6k<0(k≠0)若不等式的解集为{x|x<−3或x>−2}，求实数k的值________.14. 不等式9−x2>0的解集是________.15. 已知集合A＝{x|x2−3x−10≤0}．(Ⅰ)若B＝{x|m−6≤x≤2m−1}，A⊆B，求实数m的取值范围；(Ⅱ)若B＝{x|m+1≤x≤2m−1}，B⊆A，求实数m的取值范围．16. 已知函数f(x)=ax2+bx−a+2．(1)若关于x的不等式f(x)>0的解集是(−1,3)，求实数a的值；(2)若b=2，a>0，解关于x的不等式f(x)>0．17. 某企业生产A，B两种产品，根据市场调查与预测，A产品的利润与投资成正比，其关系如图1；B产品的利润与投资的算术平方根成正比，其关系如图2（利润和投资单(1)分别将A、B两种产品的利润表示为投资的函数关系式；(2)已知该企业已筹集到18万元投资金，并将全部投入A，B两种产品的生产，怎样分配这18万元，才能使该企业获得最大利润？其最大利润约为多少万元？参考答案与试题解析一元二次不等式的解法练习题（1）一、选择题（本题共计 7 小题，每题 5 分，共计35分）1.【答案】B【考点】一元二次不等式的应用【解析】将不等式变形为(x+1)(2x−3)≥0，由一元二次不等式的解法得出答案．【解答】不等式−2x2+x+3≤0，即2x2−x−3≥0，即(x+1)(2x−3)≥0，解得x≤−1或，故不等式−2x2+x+3≤0的解集是{x|x≤−1或x≥}．2.【答案】D【考点】一元二次不等式的应用【解析】不等式化为x(x−7)<0，求出解集即可．【解答】不等式x2−7x<0可化为x(x−7)<0，解得0<x<7，所以不等式的解集是{x|0<x<7}．3.【答案】D【考点】一元二次不等式的解法【解析】将不等式左边因式分解可得：(x+3)(x−1)≥0，从而可解不等式．【解答】解：由题意，不等式可化为：(x+3)(x−1)≥0，∴x≤−3或x≥1.故选D．4.【答案】B【考点】直接解一元二次不等式即可. 【解答】解：∵ x 2−4x −5>0， ∴ (x −5)(x +1)>0， 解得，x <−1或x >5. 故选B . 5.【答案】 D【考点】一元二次不等式的解法 【解析】 此题暂无解析 【解答】 此题暂无解答 6.【答案】 C【考点】其他不等式的解法 【解析】由题意可得，{−1<x <30<x <1 ，解不等式可求．【解答】由题意可得，{−1<x <30<x <1 ，即可得，0<x <1． 7. 【答案】 D【考点】 交集及其运算 【解析】化简集合A 、B ，根据交集的定义写出A ∩B ． 【解答】集合A ＝{x ∈N|−2<x <4}＝{0, 1, 2, 3}， B ={x|12≤2x ≤4}={x|−1≤x ≤2}，则A ∩B ＝{0, 1, 2}．二、 多选题 （本题共计 2 小题 ，每题 5 分 ，共计10分 ） 8.【答案】 B,D【考点】此题暂无解析【解答】此题暂无解答9.【答案】A,C,D【考点】二次函数的图象二次函数的性质【解析】结合二次函数的零点及单调性及复合函数的单调性与最值的关系分别检验各选项即可判断．【解答】因为二次函数对应的一元二次方程的判别式△＝(−6)2−4×3×(−1)＝48>0，所以函数f(x)有两个不同的零点，A正确；因为二次函数f(x)图象的对称轴为x＝1，且图象开口向上，所以f(x)在(1, +∞)上单调递增，B不正确；令t＝a x，则f(a x)＝g(t)＝3t2−6t−1＝3(t−1)2−4．当a>1时，1a ≤t≤a，故g(t)在[1a,a]上先减后增，又a+1a2>1，故最大值为g(a)＝3a2−6a−1＝8，解得a＝3（负值舍去）．同理当0<a<1时，a≤t≤1a ，g(t)在[a,1a]上的最大值为g(1a)=3a2−6a−1=8，解得a=13（负值舍去）．三、填空题（本题共计 5 小题，每题 5 分，共计25分）10.【答案】【考点】集合的包含关系判断及应用【解析】此题暂无解析【解答】解：已知A={−1,0,2}, B={2,a2}，若B⊆A，则a2=0，解得：a=0.故答案为：0.11.【答案】(1, 5)【考点】由题意利用绝对值不等式的基本性质，求得不等式|x−3|<2的解集．【解答】不等式|x−3|<2，即−2<x−3<2，求得1<x<5，12.【答案】{x|x>3或x<−1}【考点】一元二次不等式的解法【解析】先化简不等式，然后根据十字相乘法求出不等式的解集.【解答】解：由题意得，不等式化简为x2−2x−3>0，所以(x−3)(x+1)>0，解得x>3或x<−1，所以不等式的解集为{x|x>3或x<−1}.故答案为：{x|x>3或x<−1}.13.【答案】−2 5【考点】一元二次不等式的解法【解析】（1）由题设条件，根据二次函数与方程的关系，得：k<0，且−3，−2为关于x的方程k x2−2x+6k=0的两个实数根，再由韦达定理能求出k的值．【解答】解：∵不等式kx2−2x+6k<0(k≠0)的解集为{x|x<−3或x>−2}，∴−3和−2是方程kx2−2x+6k=0的两个根，∴−3+(−2)=2k，∴k=−25，故答案为：−25.14.【答案】{x|−3<x<3}【考点】一元二次不等式的解法【解析】此题暂无解析【解答】解：不等式9−x2>0变形为x2<9，所以解集为{x|−3<x <3}. 故答案为：{x|−3<x <3}.四、 解答题 （本题共计 3 小题 ，每题 10 分 ，共计30分 ） 15.【答案】集合A ＝{x|x 2−3x −10≤0}＝{x|−2≤x ≤5}， （1）∵ A ⊆B ，∴ {m −6≤−22m −1≥5 ，解得：3≤m ≤4，∴ 实数m 的取值范围为：[3, 4]； （2）∵ B ⊆A ，①当B ＝⌀时，m +1>2m −1，即m <2，②当B ≠⌀时，{m +1≤2m −1m +1≥−22m −1≤5，解得：2≤m ≤3，综上所述，实数m 的取值范围为：(−∞, 3]． 【考点】集合的包含关系判断及应用 【解析】先求出集合A ，再利用集合A 与集合B 的包含关系，列出不等式组，即可求出m 的取值范围，注意对空集的讨论． 【解答】集合A ＝{x|x 2−3x −10≤0}＝{x|−2≤x ≤5}， （1）∵ A ⊆B ，∴ {m −6≤−22m −1≥5 ，解得：3≤m ≤4，∴ 实数m 的取值范围为：[3, 4]； （2）∵ B ⊆A ，①当B ＝⌀时，m +1>2m −1，即m <2，②当B ≠⌀时，{m +1≤2m −1m +1≥−22m −1≤5 ，解得：2≤m ≤3，综上所述，实数m 的取值范围为：(−∞, 3]． 16.【答案】解：(1)∵ f (x )=ax 2+bx −a +2>0的解集为(−1,3)， ∴ 方程ax 2+bx −a +2=0的两根为−1和3，且a <0， ∴ {−1+3=−ba ,−1×3=−a +2a ,解得{a =−1,b =2,∴ a 的值为−1.(2)∵ b =2，a >0，∴ 方程f (x )=0的两根为−1和a−2a，∴ 当−1>a−2a即a <1时，x <a−2a或x >−1；当−1=a−2a即a =1时，x ≠−1； 当−1<a−2a即a >1时，x <−1或x >a−2a，∴ 综上，当0<a <1时，原不等式解集为{x|x <a−2a或x >−1}；当a =1时，原不等式解集为{x|x ≠−1}； 当a >1时，原不等式解集为{x|x <−1或x >a−2a}.【考点】一元二次不等式的解法 【解析】左侧图片未给出解析 左侧图片未给出解析【解答】解：(1)∵ f (x )=ax 2+bx −a +2>0的解集为(−1,3)， ∴ 方程ax 2+bx −a +2=0的两根为−1和3，且a <0， ∴ {−1+3=−ba ,−1×3=−a +2a ,解得{a =−1,b =2,∴ a 的值为−1．(2)∵ b =2，a >0，∴ f (x )=ax 2+2x −a +2=(x +1)(ax −a +2)>0， ∴ 方程f (x )=0的两根为−1和a−2a，∴ 当−1>a−2a即a <1时，x <a−2a或x >−1；当−1=a−2a即a =1时，x ≠−1； 当−1<a−2a即a >1时，x <−1或x >a−2a，∴ 综上，当0<a <1时，原不等式解集为{x|x <a−2a或x >−1}；当a =1时，原不等式解集为{x|x ≠−1}； 当a >1时，原不等式解集为{x|x <−1或x >a−2a}.17.f(x)=k1x(x≥0)，g(x)=k2√x(x≥0)，由图1，得f(1)=14，所以k1=14，则f(x)=14x(x≥0).由图2，得g(4)=4，所以k2=2，则g(x)=2√x(x≥0).(2)设B产品投入x万元，A产品投入(18−x)万元，该企业可获总利润为y万元，则y=14(18−x)+2√x，0≤x≤18.令√x=t，t∈[0, 3√2]，则y=14(−t2+8t+18)=−14(t−4)2+172.所以当t=4时，y max=172=8.5，所以x=16，18−x=2．所以当A、B两种产品分别投入2万元、16万元时，可使该企业获得最大利润8.5万元. 【考点】二次函数在闭区间上的最值函数模型的选择与应用【解析】此题暂无解析【解答】解：(1)根据题意可设A，B两种产品的利润与投资的函数关系式分别为：f(x)=k1x(x≥0)，g(x)=k2√x(x≥0)，由图1，得f(1)=14，所以k1=14，则f(x)=14x(x≥0).由图2，得g(4)=4，所以k2=2，则g(x)=2√x(x≥0).(2)设B产品投入x万元，A产品投入(18−x)万元，该企业可获总利润为y万元，则y=14(18−x)+2√x，0≤x≤18.令√x=t，t∈[0, 3√2]，则y=14(−t2+8t+18)=−14(t−4)2+172.所以x=16，18−x=2．所以当A、B两种产品分别投入2万元、16万元时，可使该企业获得最大利润8.5万元.试卷第11页，总11页。

微专题05 一元二次不等式、分式不等式【知识点总结】 一、一元二次不等式一元二次不等式20(0)ax bx c a ++>≠，其中24b ac ∆=-，12,x x 是方程20(0)ax bx c a ++>≠的两个根，且12x x <（1）当0a >时，二次函数图象开口向上． （2）①若0∆>，解集为{}21|x x x x x ><或． ②若0∆=，解集为|2b x x R x a ⎧⎫∈≠-⎨⎬⎩⎭且． ③若0∆<，解集为R ．（2） 当0a <时，二次函数图象开口向下． ①若0∆>，解集为{}12|x x x x << ②若0∆≤，解集为∅ 二、分式不等式 （1）()0()()0()f x f xg x g x >⇔> （2）()0()()0()f x f xg x g x <⇔< （3）()()0()0()0()f x g x f x g x g x ≥⎧≥⇔⎨≠⎩ （4）()()0()0()0()f x g x f x g x g x ≤⎧≤⇔⎨≠⎩ 三、绝对值不等式（1）22()()[()][()]f x g x f x g x >⇔>（2）()()(()0)()()()()f x g x g x f x g x f x g x >>⇔><-或；()()(()0)()()()f x g x g x g x f x g x <>⇔-<<；（3）含有两个或两个以上绝对值符号的不等式，可用零点分段法和图象法求解 【方法技巧与总结】（1）已知关于x 的一元二次不等式02>++c bx ax 的解集为R ，则一定满足⎩⎨⎧<∆>00a ；（2）已知关于x 的一元二次不等式02>++c bx ax 的解集为φ，则一定满足⎩⎨⎧≤∆<00a ；（3）已知关于x 的一元二次不等式02<++c bx ax 的解集为R ，则一定满足⎩⎨⎧<∆<00a ；（4）已知关于x 的一元二次不等式02<++c bx ax 的解集为φ，则一定满足⎩⎨⎧≤∆>00a ．【题型归纳目录】题型一：一元二次不等式的解法 题型二：分式不等式的解法 题型三：绝对值不等式的解法 题型四：高次不等式的解法 题型五：一元二次不等式恒成立问题 【典型例题】题型一：一元二次不等式的解法例1．（2022·全国·高一课时练习）不等式20x ax b --<的解集是{|23}x x <<，则210bx ax -->的解集是（ ） A ．{|23}x x << B ．11{|}32x x <<C ．11{|}23x x -<<- D ．{|32}x x -<<-例2．（2022·福建·厦门一中高一期中）已知关于x 的不等式20ax bx c ++<的解集为{|1x x <-或4}x >，则下列说法正确的是（ ） A ．0a > B ．不等式20ax cx b ++>的解集为{|2727}x x < C ．0a b c ++< D ．不等式0ax b +>的解集为{}|3x x >例3．（2022·江苏南京·高一期末）已知,b c ∈R ，关于x 的不等式20x bx c ++<的解集为()2,1-，则关于x 的不等式210cx bx ++>的解集为（ ） A ．1,12⎛⎫- ⎪⎝⎭B ．11,2⎛⎫- ⎪⎝⎭C ．()1,1,2∞∞⎛⎫--⋃+ ⎪⎝⎭D ．()1,1,2∞∞⎛⎫--⋃+ ⎪⎝⎭例4．（2022·全国·高一课时练习）已知不等式组22430680x x x x ⎧-+<⎨-+<⎩的解集是关于x 的不等式230x x a -+<解集的子集，则实数a 的取值范围是（ ）． A ．0a < B ．0a ≤ C ．2a ≤ D ．2a <例5．（多选题）（2022·江苏·苏州中学高一阶段练习）关于x 的不等式20ax bx c ++<的解集为(,2)(3,)-∞-⋃+∞，则下列正确的是（ ）A ．0a <B ．关于x 的不等式0bx c +>的解集为(,6)-∞-C ．0a b c ++>D ．关于x 的不等式20cx bx a -+>的解集为121,,3⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭例6．（多选题）（2022·全国·高一）若不等式20ax bx c ++>的解集为()1,2-，则下列说法正确的是（ ） A ．0a <B ．0a b c ++>C ．关于x 的不等式230bx cx a ++>解集为()3,1-D ．关于x 的不等式230bx cx a ++>解集为()(),31,-∞-⋃+∞例7．（2022·全国·高一专题练习）关于x 的不等式22430(0)x ax a a -+-≥>的解集为[]12,x x ，则12123a x x x x ++的最小值是_____________．例8．（2022·江苏·盐城市大丰区新丰中学高一期中）已知关于x 的一元二次不等式220bx x a -->的解集为{|}x x c ≠，且a ，b ，R c ∈，0b c +≠，则2210a b b c+++的最小值为_______．题型二：分式不等式的解法 例9．（2022·河南·高一期中）不等式351x x x +>-的解集是______．例10．（2022·全国·高一专题练习）不等式3113x x+>--的解集是_______．例11．（2022·湖南·新邵县第二中学高一开学考试）不等式2131x x +>-的解是___________．例12．（2022·上海市延安中学高一期中）已知关于x 的不等式221037kx kx x x -+≤-+的解集为空集，则实数k 的取值范围是___________．例13．（2022·湖北·武汉市钢城第四中学高一阶段练习）不等式301x x -≥+的解集是____________．例14．（2022·上海市奉贤区曙光中学高一阶段练习）设关于x 的不等式0ax b +>的解集为(,1)-∞，则关于x 的不等式06ax bx -≥-的解集为______；例15．（2022·黑龙江·牡丹江市第三高级中学高一开学考试）若不等式2510ax x ++≤的解集为1123x x ⎧⎫-≤≤-⎨⎬⎩⎭，则不等式13x a x -≤-的解集为______．例16．（2022·上海·高一专题练习）关于x 的不等式212x ax -≤--的解集是523x x ⎧⎫≤<⎨⎬⎩⎭，则a 的值为____．题型三：绝对值不等式的解法例17．（2022·上海交大附中高一阶段练习）不等式组12511x x ⎧-≤⎪⎨≥⎪+⎩的解集为______________；例18．（2022·上海交大附中高一期中）已知集合102x A xx ⎧⎫-=≤⎨⎬+⎩⎭，{|}1||2B x x =-≤，则A B ＝___．例19．（2022·上海浦东新·高一期中）不等式221x x ->+的解集是_________．例20．（2022·全国·高一专题练习）设集合A ＝{x ||x ﹣a |＜1，x ∈R }，B ＝{x |1＜x ＜5，x ∈R }，若A 是B 的真子集，则a 的取值范围为___．题型四：高次不等式的解法例21．（2022·全国·高一课时练习）不等式22132x x x +≥-+的解集为___________．例22．（2022·天津·静海一中高一阶段练习）不等式()()222344032x x x x x+-+≤+-的解集为___________．例23．（2022·上海·华师大二附中高一阶段练习）不等式201712xx x <≤-+的解集为________．例24．（2022·上海·华师大二附中高一期末）不等式2411x x x --≥-的解集为______．例25．（2022·上海·高一专题练习）不等式()()()()2321120x x x x ++--≤的解集为________例26．（2022·浙江·诸暨中学高一期中）不等式()()2160x x x -+-<的解集为______．例27．（2022·上海·高一专题练习）不等式()()22221221x x x x x x ++>++的解集为_________．例28．（2022·上海市复兴高级中学高一期中）不等式()()()()2233021x x x x x --≥-+-的解集是______．例29．（2022·贵州·遵义航天高级中学高一阶段练习）不等式()()232101xx x x -++≤-的解集为（ ）A ．[－1，2]B ．[－2，1]C ．[－2，1）∈（1，3]D ．[－1，1）∈（1，2]题型五：一元二次不等式恒成立问题例30．（2022·江苏·高一专题练习）若正实数,x y 满足244x y xy ++=，且不等式()2222340x y a a xy +++-≥恒成立，则实数a 的取值范围是（ ） A ．532⎡⎤-⎢⎥⎣⎦，B ．(]5,3,2⎡⎫-∞-+∞⎪⎢⎣⎭C ．532⎛⎤- ⎥⎝⎦，D ．(]5,3,2⎛⎫-∞-+∞ ⎪⎝⎭例31．（2022·全国·高一单元测试）在R 上定义运算():1x y x y ⊗⊗=-．若不等式()()1x a x a -⊗+<对任意实数x 都成立，则实数a 的取值范围为（ ）A ．1322a a ⎧⎫-<<⎨⎬⎩⎭B ．{}02a a <<C ．{}11a a -<<D ．3122a a ⎧⎫-<<⎨⎬⎩⎭例32．（2022·河南濮阳·高一期末（理））已知命题“R x ∀∈，214(2)04x a x +-+>”是假命题，则实数a 的取值范围为（ ） A ．(][),04,-∞+∞ B ．[]0,4 C ．[)4,+∞ D ．()0,4例33．（2022·浙江·金华市曙光学校高一阶段练习）“不等式20x x m -+>在R 上恒成立”的充要条件是（ ） A ．14m >B ．14m <C ．1m <D ．1m例34．（2022·四川·广安二中高一阶段练习（理））已知关于x 的不等式()()221110a x a x ----<的解集为R ，则实数a 的取值范围（ ） A ．3,15⎛⎫- ⎪⎝⎭B ．3,15⎛⎤- ⎥⎝⎦C ．[)3,1,5⎛⎫-∞-⋃+∞ ⎪⎝⎭D ．()3,1,5⎛⎫-∞-⋃+∞ ⎪⎝⎭例35．（2022·全国·高一单元测试）已知12x ≤≤，20x ax ->恒成立，则实数a 的取值范围是（ ） A ．{}1a a ≥ B ．{}1a a > C ．{}1a a ≤ D ．{}1a a <例36．（2022·陕西安康·高一期中）若对任意的2[1,0],2420x x x m ∈--+++≥恒成立，则m 的取值范围是（ ） A ．[4,)+∞ B ．[2,)+∞ C ．(,4]-∞ D ．(,2]-∞例37．（2022·广西·南宁市东盟中学高一期中）已知命题“21,2,2102x x ax ⎡⎤∃∈-+≤⎢⎥⎣⎦”为假命题，则实数a 的取值范围是（ ） A ．2222a -<B ．22a <C ．3a <D ．92a <例38．（2022·全国·高一课时练习）已知命题p ：“15x ∃≤≤，250x ax -->”为真命题，则实数a 的取值范围是（ ）A ．4a <B ．4aC ．4a >D ．4a >-【过关测试】 一、单选题1．（2022·江西·丰城九中高一期末）已知集合{}2870A x x x =-+<，{}14B x x =<<，则“x A ∈”是“x B ∈”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件2．（2022·全国·高一）若关于x 的不等式()2330x m x m -++<的解集中恰有3个整数，则实数m 的取值范围为（ ） A ．(]6,7B ．[)1,0-C ．[)(]1,06,7-⋃D ．[]1,7-3．（2022·江苏·高一专题练习）若存在正实数y ，使得54y xx y xy-=+，则实数x 的最大值为（ ） A ．15B ．54C ．1D ．44．（2022·江苏·高一）已知关于x 的不等式ax b >的解集是{|2}x x <，则关于x 的不等式()()10ax b x +->的解集是（ ）A ．()()12-∞⋃+∞，， B ．()12， C ．()()21-∞-⋃+∞，， D ．()21-，5．（2022·全国·高一课时练习）关于x 的不等式22(11)m x mx m x +<+++对R x ∈恒成立，则实数m 的取值范围是（ ） A ．(0)∞-，B ．30,(4)⎛⎫∞+∞⎪- ⎝⎭，C ．(]0-∞，D ．(]40,3∞∞⎛⎫-⋃+ ⎪⎝⎭，6．（2022·江苏·高一）已知不等式20ax bx c ++>的解集为{}|21x x -<<，则不等式20cx bx a -+<的解集为（ ） A ．11,2⎛⎫- ⎪⎝⎭B ．1,12⎛⎫- ⎪⎝⎭C ．1,12⎛⎫ ⎪⎝⎭D ．()2,1-7．（2022·北京师大附中高一期末）关于x 的不等式21x x a x +≥-对任意x ∈R 恒成立，则实数a 的取值范围是（ ） A ．[]1,3- B ．(],3-∞ C ．(],1-∞D ．(][),13,-∞⋃+∞8．（2022·广西·桂林中学高一期中）已知0ax b ->的解集为(,2)-∞，关于x 的不等式2056ax bx x +≥--的解集为（ ）A ．(,2](1,6)-∞--B ．(,2](6,)-∞-+∞C ．[2,1)(1,6)---D ．[2,1)(6,)--+∞ 二、多选题9．（2022·湖北黄石·高一阶段练习）下列结论错误的是（ ） A ．不存在实数a 使得关于x 的不等式210ax x ++≥的解集为∅B ．不等式20ax bx c ++≤在R 上恒成立的必要条件是0a <且240b ac ∆=-≤C ．若函数()20y ax bx c a =++≠对应的方程没有实根，则不等式20ax bx c ++>的解集为RD ．不等式11x>的解集为1x < 10．（2022·黑龙江·尚志市尚志中学高一阶段练习）设p ：实数x 满足1021x x -≤-，则p 成立的一个必要不充分条件是（ ） A ．11?2x ≤≤ B ．112x <≤ C ．01x ≤≤ D ．01x <≤11．（2022·江苏南京·高一阶段练习）定义区间(),m n 的长度为n m -，若满足()()2012x ax x -<--的x 构成的区间的长度之和为3，则实数a 的可能取值是（ ）A ．14B ．13C ．3D ．412．（2022·全国·高一专题练习）下列条件中，为 “关于x 的不等式210mx mx -+>对R x ∀∈恒成立”的充分不必要条件的有（ ） A ．04m ≤< B ．02m << C ．14m << D ．16m -<<三、填空题13．（2022·广东·梅州市梅江区梅州中学高一阶段练习）二次函数y ＝ax 2＋bx ＋c （a ≠0）的图象如图所示，则不等式（ax +b ）（cx -b ）<0的解集是________．14．（2022·江苏·南京市金陵中学河西分校高一阶段练习）若对任意R x ∈，2222224x ax bx c x x +≤++≤-+ 恒成立，则ab 的最大值为_________．15．（2022·江苏·扬州大学附属中学高一期中）不等式20ax bx c ++≤的解集为R ，则2222b a c +的最大值为____________．16．（2022·上海·格致中学高一期末）已知关于x 的不等式()226300x ax a a -+-≥>的解集为[]12,x x ，则12123ax x x x ++的最小值是___________．。