北师大版九年级下册数学2.3.1确定二次函数表达式测试解析版

北师大初中数学九年级重点知识精选掌握知识点，多做练习题，基础知识很重要！北师大初中数学和你一起共同进步学业有成！2.3 确定二次函数的表达式类型一：已知顶点和另外一点用顶点式已知一个二次函数的图象过点（0，1），它的顶点坐标是（8，9），求这个二次函数关系式．练习：已知抛物线的顶点是（－1，－2），且过点（1，10），求其解析式类型二：已知图像上任意三点（现一般有一点在y轴上）用一般式已知二次函数的图象过（0，1）、（2，4）、（3，10）三点，求这个二次函数的关系式．练习：已知抛物线过三点：（－1，2），（0，1），（2，－7）．求解析式类型三：已知图像与x轴两个交点坐标和另外一点坐标，用两根式已知二次函数的图象过（-2，0）、（4，0）、（0，3）三点，求这个二次函数的关系式．练习：已知抛物线过三点：（－1，0）、（1，0）、（0，3）．（1）.求这条抛物线所对应的二次函数的关系式；（2）写出它的开口方向、对称轴和顶点坐标；（3）这个函数有最大值还是最小值？这个值是多少？巩固练习：1.已知二次函数的图象过（3，0）、（2，-3）二点,且对称轴是x=1，求这个二次函数的关系式．2..已知二次函数的图象过（3，-2）、（2，-3）二点,且对称轴是x=1，求这个二次函数的关系式．3.已知二次函数的图象与x轴交于A，B两点，与y轴交于点C。

若AC=20,BC=15,∠ACB=90°，试确定这个二次函数的解析式4.已知一个二次函数当x=8时,函数有最大值9,且图象过点（0，1）,求这个二次函数的关系式．小测：1.二次函数y=x2－2x－k的最小值为－5，则解析式为。

x2.若一抛物线与轴两个交点间的距离为8，且顶点坐标为（1, 5），则它们的解析式为。

3.已知一个二次函数的图象经过点(6,0),且抛物线的顶点是(4,－8)，求它的解析式。

4.已知二次函数y＝ax2＋bx＋c的图象顶点坐标为(－2，3)，且过点(1，0)，求此二次函数的解析式．5．已知二次函数y＝ax2＋bx＋c，当x＝－1时有最小值－4，且图象在x轴上截得线段长为4，求函数解析式．6．抛物线y＝ax2＋bx＋c经过(0，0)，(12，0)两点，其顶点的纵坐标是3，求这个抛物线的解析式．7.已知二次函数y=ax2＋bx＋c，当x=0时，y=0；x=1时，y=2；x=-1时，y=1．求a、b、c，并写出函数解析式．8.已知抛物线y＝ax2经过点A(2，1)．(1)求这个函数的解析式；(2)写出抛物线上点A关于y轴的对称点B的坐标；(3)求△OAB的面积；(4)抛物线上是否存在点C，使△ABC的面积等于△OAB面积的一半，若存在，求出C点的坐标；若不存在，请说明理由．相信自己，就能走向成功的第一步教师不光要传授知识，还要告诉学生学会生活。

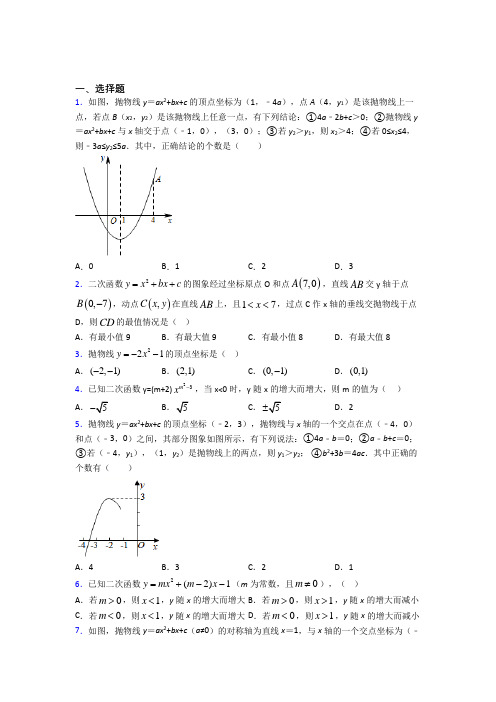
一、选择题1．如图，抛物线y ＝ax 2+bx +c 的顶点坐标为（1，﹣4a ），点A （4，y 1）是该抛物线上一点，若点B （x 2，y 2）是该抛物线上任意一点，有下列结论：①4a ﹣2b +c ＞0；②抛物线y ＝ax 2+bx +c 与x 轴交于点（﹣1，0），（3，0）；③若y 2＞y 1，则x 2＞4；④若0≤x 2≤4，则﹣3a ≤y 2≤5a ．其中，正确结论的个数是（ ）A ．0B ．1C ．2D ．32．二次函数2y x bx c =++的图象经过坐标原点O 和点()7,0A ，直线AB 交y 轴于点()0,7B -，动点(),C x y 在直线AB 上，且17x <<，过点C 作x 轴的垂线交抛物线于点D ，则CD 的最值情况是（ ）A ．有最小值9B ．有最大值9C ．有最小值8D ．有最大值8 3．抛物线221y x =--的顶点坐标是（ ）A ．(2,1)--B ．(2,1)C ．(0,1)-D ．(0,1) 4．已知二次函数y=(m+2)23mx -，当x<0时，y 随x 的增大而增大，则m 的值为（ ） A ．5- B ．5C ．5±D ．2 5．抛物线y ＝ax 2+bx +c 的顶点坐标（﹣2，3），抛物线与x 轴的一个交点在点（﹣4，0）和点（﹣3，0）之间，其部分图象如图所示，有下列说法：①4a ﹣b ＝0；②a ﹣b +c ＝0； ③若（﹣4，y 1），（1，y 2）是抛物线上的两点，则y 1＞y 2； ④b 2+3b ＝4ac ．其中正确的个数有（ ）A ．4B ．3C ．2D ．16．已知二次函数2(2)1y mx m x =+--（m 为常数，且0m ≠），（ ）A ．若0m >，则1x <，y 随x 的增大而增大B ．若0m >，则1x >，y 随x 的增大而减小C ．若0m <，则1x <，y 随x 的增大而增大D ．若0m <，则1x >，y 随x 的增大而减小 7．如图，抛物线y ＝ax 2+bx +c （a ≠0）的对称轴为直线x ＝1，与x 轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①a ＞0；②b ＞0； ③方程ax 2+bx +c ＝0的两个根是x 1＝﹣1，x 2＝3；④当y ＞0时，x 的取值范围是﹣1＜x ＜3；其中结论正确的个数是（ ）A ．4个B ．3个C ．2个D ．1个8．如图，已知二次函数()20y ax bx c a =++≠的图象与x 轴交于点()1,0A -，对称轴为直线1x =，下列结论：①0abc <；②930a b c ++=；③20a b +=；④2am bm a b +<+（m 是任意实数），其中正确的是（ ）A ．①②B ．②③C ．①②③D ．②③④ 9．如图，抛物线22y x x m =-+交x 轴于点(),0A a ，(),0Bb ，交y 轴于点C ，抛物线的顶点为D ，下列四个结论：①无论m 取何值，2CD =恒成立；②当0m =时，ABD △是等腰直角三角形；③若2a =-，则6b =；④()11,P x y ，()22,Q x y 是抛物线上的两点，若121x x ，且122x x +>，则12y y <．正确的有（ ）A ．①②③④B ．①②④C ．①②D ．②③④10．如图，在平面直角坐标系中，反比例函数和二次函数的图象大致如图所示，它们的表达式可能分别为（ ）A ．2,k y y kx x x =-=-+B ．2,k y y kx x x =-=--C ．2,k y y kx x x ==--D ．2,k y y kx x x==-+ 11．在同一直角坐标系中，一次函数y ax c =+和二次函数2y ax c =--的图象可能为（ ）A ．B ．C ．D ． 12．函数k y x=与()20y kx k k =-≠在同一直角坐标系中的图象大致是下图中的（ ） A ． B ． C ． D ．二、填空题13．如图，正方形ABCD 中，AD =4,AE =3DE ,点P 在AB 上运动（不与A 、B 重合），过点P 作PQ ⊥EP ，交CB 于点Q ，则BQ 的最大值是______．14．将抛物线2112y x =+绕原点O 旋转180︒，得到的抛物线解析式为__________． 15．计算机可以帮助我们又快又准地画出函数的图像．用“几何画板”软件画出的函数2(3)y x x =-和3y x =-的图像如图所示．若m ，n 分别满足方程2(3)1x x -=和31x -=根据图像可知m ，n 的大小关系是___________．16．如图，点P 是双曲线()4:0C y x x=>上的一点，过点P 作x 轴的垂线交直线1:22AB y x =-于点Q ，连结,OP OQ 当点P 在曲线C 上运动，且点P 在Q 的上方时，POQ △面积的最大值是________．17．把函数y ＝x 2＋3的图像向下平移1个单位长度得到的图像对应的函数关系式为________．18．在平面直角坐标系中，已知()1,A m -和()5,B m 是抛物线21y x bx =++上的两点，则抛物线21y x bx =++的顶点坐标为_________．19．将抛物线243y x x =-+沿x 轴向左平移2个单位，则平移后抛物线的解析式是__． 20．已知A （0，y 1），B （1，y 2），C （4，y 3）是抛物线y =x 2﹣3x 上的三点，则y 1，y 2，y 3的大小关系为____．（用“＜”符号连接）三、解答题21．如图，抛物线y ＝x 2+bx +c 经过点（1，﹣4）和（﹣2，5），请解答下列问题：（1）求抛物线的解析式，并求出对称轴及顶点坐标；（2）若与x 轴的两个交点为A 、B ，与y 轴交于点C ．在该抛物线上找一点D ，使得△ABC 与△ABD 全等，求出D 点的坐标．22．定义：对于已知的两个函数，任取自变量x 的一个值，当0x ≥时，它们对应的函数值互为相反数；当0x <时，它们对应的函数值相等，我们称这样的两个函数互为相关函数．例如：正比例函数y x =，它的相关函数为(0)(0)x x y x x -≥⎧=⎨<⎩． （1）已知点(1,3)A -在一次函数2y ax =-的相关函数的图象上，求a 的值；（2）已知二次函数2283y x x =-+-．①当点(,4)B m -在这个函数的相关函数的图象上时，求m 的值；②当23x -≤≤时，求函数2283y x x =-+-的相关函数的最大值和最小值． 23．已知：抛物线y 1＝﹣x 2﹣2x +3的图象交x 轴于点A ，B （点A 在点B 的左侧）． （1）请在平面直角坐标系内画出二次函数y 1＝﹣x 2﹣2x +3的草图，并标出点A 的位置； （2）点C 是直线y 2＝﹣x +1与抛物线y 1＝﹣x 2﹣2x +3异于B 的另一交点，则点C 的坐标为 ；当y 1≥y 2时x 的取值范围是 ．24．如图，在平面直角坐标系中，(0,1)A ，(2,0)B ，将线段AB 绕原点O 逆时针旋转90°，得到线段A B ''，且点A '，B '，B 均在抛物线上．（1）求该抛物线的函数表达式．（2）该抛物线的对称轴上有一点Q ，使ABQ △是以AB 为直角边的直角三角形，求Q 点的坐标．25．已知二次函数22y x x m =++的图象与x 轴有且只有一个公共点．（1）求该二次函数的图象的顶点坐标；（2）若()1,Pn y ，()22,Q n y +是该二次函数的图象上的两点，且12y y >，求实数n 的取值范围．26．如图，一农户要建一矩形猪舍，猪舍的一边利用长为12m 的住房墙，另外三边用27m 长的建筑材料围成，为了方便进出，在垂直于住房墙的一边留一个1m 宽的门．所围成矩形猪舍的长、宽分别为多少时，猪舍的面积最大，最大面积是多少？【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】利用对称轴公式和顶点坐标得出﹣4a ＝a +b +c ，b ＝﹣2a ，c ＝﹣3a ，则可对①进行判断；抛物线解析式为y ＝ax 2﹣2ax ﹣3a ，配成交点式得y ＝a （x ﹣3）（x +1），可对②进行判断；根据二次函数对称性和二次函数的性质可对③进行判断；计算x ＝4时，y ＝5a ，则根据二次函数的性质可对④进行判断．【详解】解：①∵二次函数y ＝ax 2+bx +c （a ≠0）的顶点坐标为（1，﹣4a ），∴x ＝﹣2b a＝1，且﹣4a ＝a +b +c ， ∴b ＝﹣2a ，c ＝﹣3a ，∵抛物线开口向上，则a ＞0， ∴4a ﹣2b +c ＝4a +4a ﹣3a ＝5a ＞0，故结论①正确；②∵b ＝﹣2a ，c ＝﹣3a ，∴y ＝ax 2﹣2ax ﹣3a ＝a （x ﹣3）（x +1），∴抛物线y ＝ax 2+bx +c 与x 轴交于点（﹣1，0），（3，0），故结论②正确；③∵点A （4，y 1）关于直线x ＝1的对称点为（﹣2，y 1），∴当y 2＞y 1，则x 2＞4或x 2＜﹣2，故结论③错误；④当x ＝4时，y 1＝16a +4b +c ＝16a ﹣8a ﹣3c ＝5a ，∴当0≤x 2≤4，则﹣4a ≤y 2≤5a ，故结论④错误．故选：C ．【点睛】本题考查了二次函数的图象与性质，掌握二次函数图象与性质的相关知识并能灵活运用所学知识求解是解题的关键．2．B解析：B【分析】根据待定系数法求得抛物线的解析式和AB 的解析式，设(,7)C x x -，则2(,7)D x x x -，根据图象的位置即可得出2(4)9CD x =--+，根据二次函数的性质即可求得．【详解】 解：二次函数2y x bx c =++的图象经过坐标原点O 和点(7,0)A ， ∴04970c b c =⎧⎨++=⎩，解得70b c =-⎧⎨=⎩， ∴二次函数为27y x x =-，(7,0)A ，(0,7)B -，∴直线AB 为：7y x =-，令277x x x -=-，解得：11x =，27x =，∴点E 的横坐标为1，则点C 始终在点D 上方，设(,7)C x x -，则2(,7)D x x x -，2227(7)87(4)9CD x x x x x x ∴=---=-+-=--+，17x ∴<<范围内，有最大值9，故选：B ．【点睛】本题考查了二次函数的性质，待定系数法求一次函数的解析式，求二次函数的解析式，表示出CD 的关系式是解题的关键．3．C解析：C【分析】根据题目中的函数解析式可以直接写出该抛物线的顶点坐标．【详解】解：∵y=-2x 2-1，∴该抛物线的顶点坐标为（0，-1），故选：C ．【点睛】本题考查了二次函数的性质，解答本题的关键是明确题意，利用二次和函数的性质解答． 4．A解析：A【分析】根据次数为2可列方程，再根据函数增减性确定m 值．【详解】解：根据题意可知，232m -=， 解得，5m =∵二次函数y=(m+2)23mx -，当x<0时，y 随x 的增大而增大，∴m+2＜0，解得m ＜-2，综上，m=5-故选：A ．【点睛】本题考查了二次函数的定义和增减性，解题关键是根据二次函数的定义列方程，依据增减性确定二次项系数的符号．5．B解析：B【分析】根据抛物线的对称轴可判断①；由抛物线与x 轴的交点及抛物线的对称性以及由x ＝﹣1时y ＞0可判断②，由抛物线对称性和增减性，即可判断③；利用抛物线的顶点的纵坐标为3得到244ac b a-=3，即可判断④． 【详解】解：∵抛物线的对称轴为直线x 2b a =-=-2， ∴4a ﹣b ＝0，所以①正确；∵与x 轴的一个交点在（﹣3，0）和（﹣4，0）之间，∴由抛物线的对称性知，另一个交点在（﹣1，0）和（0，0）之间，∴x ＝﹣1时y ＞0，即a ﹣b +c ＞0，∴所以②错误；由抛物线的对称性知（﹣4，y 1）与（0，y 1）关于对称轴对称，∵抛物线开口向下，对称轴为直线x 2b a=-=-2 ∴当x ＞-2时，y 随x 的增大而减小，∵-2＜0＜1∴y 1＞y 2∴所以③正确；∵抛物线的顶点坐标为（﹣2，3）， ∴244ac b a-=3， ∴b 2+12a ＝4ac ，∵4a ﹣b ＝0，∴b ＝4a ，∴b 2+3b ＝4ac ，所以④正确；故选：B ．【点睛】本题考查了二次函数图象与系数的关系：对于二次函数y ＝ax 2+bx +c （a ≠0），二次项系数a 决定抛物线的开口方向和大小：当a ＞0时，抛物线向上开口；当a ＜0时，抛物线向下开口；一次项系数b 和二次项系数a 共同决定对称轴的位置：当a 与b 同号时（即ab ＞0），对称轴在y 轴左； 当a 与b 异号时（即ab ＜0），对称轴在y 轴右；常数项c 决定抛物线与y 轴交点位置：抛物线与y 轴交于（0，c ）：抛物线与x 轴交点个数由△决定：△＝b 2﹣4ac ＞0时，抛物线与x 轴有2个交点；△＝b 2﹣4ac ＝0时，抛物线与x 轴有1个交点；△＝b 2﹣4ac ＜0时，抛物线与x 轴没有交点．6．D解析：D【分析】先求出二次函数图象的对称轴，然后根据m 的符号分类讨论，结合图象的特征即可得出结论．【详解】 该二次函数图象的对称轴为直线21122m x m m -=-=-+， 若0m >，对于22m x m -=-无法判断其符号，故A 、B 选项不一定正确； 若0m <，则202m x m -=-<，即22m m--<1，且抛物线的开口向下， ∴当1x >时，y 随x 的增大而减小，故选：D ．【点睛】此题考查的是二次函数的图象及性质，解决此题的关键是分类讨论确定对称轴的位置，再结合开口方向进行综合分析．7．B解析：B【分析】根据抛物线与系数的关系判断即可．【详解】解：抛物线开口向下，a<0，故①错误；对称轴在y 轴右侧，a 、b 异号，b ＞0,故②正确；抛物线与x 轴交点为（﹣1，0），对称轴为直线x ＝1，根据对称性，另一个交点为（3,0），故③正确；根据图象可知，x 的取值范围是﹣1＜x ＜3时；抛物线在x 轴上方，故④正确； 故选：B ．【点睛】本题考查二次函数图象与系数的关系，解题的关键是熟练正确理解二次函数图象与系数的关系，本题属于中等题型．8．B解析：B【分析】①抛物线开口向上，对称轴为直线x ＝1，即可得出a ＞0、b ＜0、c ＜0，进而可得出abc ＞0，结论①错误；②由抛物线的对称轴以及与x 轴的一个交点坐标，可得出另一交点坐标为（3，0），进而可得出9a ＋3b ＋c ＝0，结论②正确；③由对称轴直线x=1，可得结论③正确；④2()()0am bm a b +-+≥，可得结论④错误．综上即可得出结论．【详解】解：①∵抛物线开口向上，对称轴为直线x ＝1，∴a ＞0，12b a-=，c ＜0， ∴b ＝−2a ＜0，∴abc ＞0，结论①错误； ②∵二次函数y ＝ax 2＋bx ＋c （a≠0）的图象与x 轴交于点A （−1，0），对称轴为直线x ＝1，∴二次函数y ＝ax 2＋bx ＋c （a≠0）的图象与x 轴的另一个交点为（3，0），∴9a ＋3b ＋c ＝0，结论②正确；③∵对称轴为直线x ＝1， ∴12b a-=，即：b ＝−2a ， ∴20a b +=，结论③正确；④∵222()()(2)(2)2am bm a b am am a a am am a +-+=---=-+22(21)(1)a m m a m =-+=-≥0，∴2am bm a b +≥+，结论④错误．综上所述，正确的结论有：②③．故选：B ．【点睛】本题考查了抛物线与x 轴的交点、二次函数图象与系数的关系、二次函数的性质以及二次函数图象上点的坐标特征，逐一分析四条结论的正误是解题的关键．9．B解析：B【分析】①先求出C 、D 的坐标，再根据两点距离公式求得CD ，便可判断；②当m=0时，可得抛物线与x 轴的两个交点坐标和顶点坐标即可判断；③根据抛物线与x 轴的一个交点坐标和对称轴即可得另一个交点坐标即可判断； ④根据二次函数图象当x 1＜1＜x 2，且x 1+x 2＞2，根据离对称越远的点的纵坐标就越大得出结论．【详解】解：①∵y=x 2-2x+m=（x-1）2+m-1，∴C （0，m ），D （1，m-1），∴，故①正确；②当m=0时，抛物线与x 轴的两个交点坐标分别为A （0，0）、B （2，0），顶点D （1，-1），∴，∴△ABD是等腰直角三角形，故②正确；③当a=-2时，抛物线与x轴的一个交点坐标为（-2，0），∵对称轴x=1，∴另一个交点坐标为（4，0），∴b=4，故③错误；④观察二次函数图象可知：当x1＜1＜x2，且x1+x2＞2，则1-x1＜x2-1∴y1＜y2．故④正确．故选：B．【点睛】本题考查了二次函数图象与系数的关系、二次函数图象上点的坐标特征、抛物线与x轴的交点、等腰直角三角形，解决本题的关键是综合利用以上知识．10．D解析：D【分析】根据反比例函数图像的位置判断k的符号，再结合二次函数的图像和性质，逐项判断即可【详解】A、由反比例函数kyx=-的图像可知，0k>，则二次函数2y kx x=-+的图像开口应向下，与图像不符，故选项错误；B、由反比例函数kyx=-的图像可知，0k>，则二次函数2y kx x=--的图像开口应向下，与图像不符，故选项错误；C、由反比例函数kyx=的图像可知，0k<，则二次函数2y kx x=--的图像开口向上，对称轴11222bxa k k-=-=-=->-应位于y轴的右侧，与图像不符，故选项错误；D、由反比例函数kyx=的图像可知，0k<，则二次函数2y kx x=-+的图像开口向上，对称轴11222bxa k k=-=-=<-应位于y轴的左侧，与图像相符，故选项正确；故选：D．【点睛】本题考查了反比例函数，二次函数图像的性质，解题关键是熟练掌握反比例函数和二次函数的图像和性质．11．D解析：D【分析】根据二次函数的开口方向，与y轴的交点；一次函数经过的象限，与y轴的交点可得相关图象．【详解】解：∵一次函数经过y轴上的（0，c），二次函数经过y轴上的（0，-c），∴两个函数图象交于y轴上的不同点，故A，C选项错误；当a＜0，c＜0时，二次函数开口向上，一次函数经过二、三、四象限，故B选项错误；当a＜0，c＞0时，二次函数开口向上，一次函数经过一、二、四象限，故D选项正确；故选：D．【点睛】本题考查二次函数及一次函数的图象的性质；用到的知识点为：二次函数和一次函数的常数项是图象与y轴交点的纵坐标；一次函数的一次项系数大于0，图象经过一、三象限；小于0，经过二、四象限；二次函数的二次项系数大于0，图象开口向上；二次项系数小于0，图象开口向下．12．B解析：B【分析】根据k>0，k<0，结合反比例函数及二次函数图象及其性质分类讨论．【详解】解：分两种情况讨论：①当k>0时，反比例函数kyx=在一、三象限，而二次函数()20y kx k k=-≠开口向上，与y轴交点在原点下方，故C选项错误，B选项正确；②当k<0时，反比例函数kyx=在二、四象限，而二次函数()20y kx k k=-≠开口向下，与y轴交点在原点上方，故A选项与D选项错误．故选B．【点睛】本题考查了反比例函数图象性质和二次函数图象性质．关键是根据k>0，k<0，结合反比例函数及二次函数图象及其性质分类讨论．二、填空题13．【分析】先由正方形的性质及PQ⊥EP得出∠AEP=∠BPQ∠A=∠B=90°从而可判定△APE∽△BQP根据相似三角形的性质得出比例等式；再根据AD=4AE=3DE 得出AE 和DE 的长然后设BQ=yA 解析：43【分析】先由正方形的性质及PQ ⊥EP ，得出∠AEP=∠BPQ ，∠A=∠B=90°，从而可判定△APE ∽△BQP ，根据相似三角形的性质得出比例等式；再根据AD=4，AE=3DE ，得出AE 和DE 的长，然后设BQ=y ，AP=x ，则BP=4-x ，将相关数据代入比例等式，变形得出y 关于x 的二次函数，配方，即可得出答案.【详解】解：在正方形ABCD 中，∠A=∠B=90°，且PQ ⊥EP∴∠AEP+∠APE=90°， ∠QPB+∠APE=90°∴∠AEP=∠BPQ又∠A=∠B=90°∴△APE ∽△BQP ∴AE AP BP BQ=， 又AD=4，AE=3DE ，∴AE=334AD =，DE=4-3=1， 设BQ=y ，AP=x ，则BP=4-x ， ∴34x x y=- 化简得：21433y x x =-+， 整理得：()214233y x =--+， ∴当x=2时，y 有最大值为43，即BQ 的最大值是43， 故答案为：43． 【点睛】 本题考查了正方形的性质、相似三角形的判定与性质及二次函数的性质，熟练掌握相关性质及定理是解题的关键.14．【分析】先确定抛物线线的顶点坐标为（01）再利用关于原点对称的点的坐标特征得到点（01）变换后所得对应点的坐标为（0-1）然后利用顶点式写出旋转后抛物线【详解】解：抛物线的顶点坐标为（01）点关于原 解析：2112y x =--【分析】 先确定抛物线线2112y x =+的顶点坐标为（0，1），再利用关于原点对称的点的坐标特征得到点（0，1）变换后所得对应点的坐标为（0，-1），然后利用顶点式写出旋转后抛物线．【详解】解：抛物线2112y x =+的顶点坐标为（0，1），点关于原点O 的对称点的坐标为（0，-1），此时旋转后抛物线的开口方向相反，所以旋转后的抛物线的解析式为2112y x =--． 故答案为：2112y x =--． 【点睛】本题考查了二次函数图象与几何变换：抛物线绕某点旋转180°得到旋转后的抛物线开口相反，抛物线的开口大小不变． 15．【分析】利用函数图象通过确定函数和的图象与直线的交点位置可得到m 与n 的大小【详解】解：方程的解为函数的图象与直线的交点的横坐标的解为一次函数与直线的交点的横坐标如图由图象得故答案为：【点睛】本题考查 解析：m n <【分析】利用函数图象，通过确定函数2(3)y x x =-和3y x =-的图象与直线1y =的交点位置可得到m 与n 的大小．【详解】解：方程2(3)1x x -=的解为函数2(3)y x x =-的图象与直线1y =的交点的横坐标，31x -=的解为一次函数3y x =-与直线1y =的交点的横坐标，如图，由图象得m n <．故答案为：m n．【点睛】本题考查了函数图象的应用，会利用图象的交点的坐标表示方程或方程组的解是解题的关键．16．3【分析】设P（x）则Q（xx−2）得到PQ＝−x＋2根据三角形面积公式得到S△POQ＝−（x−2）2＋3根据二次函数的性质即可求得最大值【详解】解：∵PQ⊥x轴∴设P（x）则Q（xx−2）∴PQ＝解析：3【分析】设P（x，4x），则Q（x，12x−2），得到PQ＝4x−12x＋2，根据三角形面积公式得到S△POQ＝−14（x−2）2＋3，根据二次函数的性质即可求得最大值．【详解】解：∵PQ⊥x轴，∴设P（x，4x ），则Q（x，12x−2），∴PQ＝4x −12x＋2，∴S△POQ＝12（4x−12x＋2）•x＝−14（x−2）2＋3，∵−14＜0，∴△POQ面积有最大值，最大值是3，故答案为：3．【点睛】本题考查了一次函数图象上点的坐标特征，二次函数的性质，反比例函数y＝kx（k≠0）系数k的几何意义：从反比例函数y＝kx（k≠0）图象上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|．17．y＝x2＋2【分析】根据向下平移纵坐标减求出平移后函数的顶点坐标再利用顶点式写出解析式即可【详解】解：函数y＝x2＋3的顶点坐标为（03）∵函数图象向下平移1个单位长度∴得到的函数图象顶点坐标为（0解析：y＝x2＋2．【分析】根据向下平移纵坐标减求出平移后函数的顶点坐标，再利用顶点式写出解析式即可．【详解】解：函数y ＝x 2＋3的顶点坐标为（0，3），∵函数图象向下平移1个单位长度，∴得到的函数图象顶点坐标为（0，2），∴得到函数解析式为y ＝x 2＋2．故答案为：y ＝x 2＋2．【点睛】本题考查了二次函数的平移变换，通过平移求出新图象顶点坐标是关键．18．（2－3）【分析】根据坐标特点判定AB 两点是一对对称点从而得到抛物线的对称轴根据对称轴x=确定b 的值从而确定顶点坐标【详解】∵和是抛物线上的两点∴抛物线对称轴为x==2∴顶点坐标的横坐标为2；∵∴b解析：（2，－3）.【分析】根据坐标特点，判定A ，B 两点是一对对称点，从而得到抛物线的对称轴，根据对称轴x=2b a-，确定b 的值，从而确定顶点坐标. 【详解】 ∵()1,A m -和()5,B m 是抛物线21y x bx =++上的两点，∴抛物线对称轴为x=152-+=2， ∴顶点坐标的横坐标为2； ∵22b -=， ∴b= -4， ∴241y x x =-+，当x=2时，22421y =-⨯+= -3，∴抛物线的顶点坐标为（2，-3），故应填（2，-3）.【点睛】本题考查了利用抛物线的对称点确定顶点坐标，熟练掌握抛物线对称轴与对称点的关系，抛物线顶点坐标的计算公式是解题的关键.19．y=x2-1【分析】先把抛物线写成顶点式再写出平移后的顶点根据顶点式可求平移后抛物线的解析式【详解】解：∴原抛物线顶点坐标为(2-1)向左平移2个单位平移后抛物线顶点坐标为(0-1)∴平移后抛物线解解析：y=x 2-1【分析】先把抛物线写成顶点式，再写出平移后的顶点，根据顶点式可求平移后抛物线的解析式．【详解】解：()22-4+3-2-1y x x x ==，∴原抛物线顶点坐标为(2，-1)，向左平移2个单位，平移后抛物线顶点坐标为(0，-1)， ∴平移后抛物线解析式为：21y x =-，故答案为：21y x =-．【点睛】本题考查了抛物线的平移与抛物线解析式的关系，关键是把抛物线的平移转化为顶点的平移，运用顶点式求抛物线的解析式． 20．y2＜y1＜y3【分析】根据二次函数的解析式得出图象的开口向上对称轴是直线x=根据x ＞时y 随x 的增大而增大即可得出答案【详解】解：∵y=x2﹣3x ∴图象的开口向上对称轴是直线x=∵A （0y1）B （1解析：y 2＜y 1＜y 3【分析】根据二次函数的解析式得出图象的开口向上，对称轴是直线x=32，根据x ＞32时，y 随x 的增大而增大，即可得出答案．【详解】解：∵y=x 2﹣3x ，∴图象的开口向上，对称轴是直线x=32． ∵A （0，y 1），B （1，y 2），C （4，y 3）是抛物线y=x 2﹣3x 上的三点，且0＜1＜32＜4， ∴y 2＜y 1＜y 3．故答案为：y 2＜y 1＜y 3．【点睛】本题主要考查对二次函数图象上点的坐标特征，二次函数的性质等知识点的理解和掌握，能熟练地运用二次函数的性质进行推理是解此题的关键．三、解答题21．（1）y ＝x 2﹣2x ﹣3，对称轴为：x ＝1，顶点（1，－4）；（2）D （2，﹣3）【分析】（1）把（1，﹣4）和（﹣2，5）代入，解方程即可；根据解析式可求对称轴和顶点坐标； （2）根据对称性确定D 点位置，求出坐标．【详解】解：（1）由题意，得14425b c b c ++=-⎧⎨-+=⎩， 解得，23b c =-⎧⎨=-⎩，所以，该抛物线的解析式为：y ＝x 2﹣2x ﹣3；抛物线y ＝x 2﹣2x ﹣3的对称轴为：2121x -=-=⨯， 把x ＝1代入y ＝x 2﹣2x ﹣3得，y =-4，∴抛物线的顶点坐标为（1，-4） （2）根据轴对称的性质，点C 关于x ＝1的对称点D 即为所求，此时，AC ＝BD ，BC ＝AD ，在△ABC 和△BAD 中， ∵AB BA AC BD BC AD =⎧⎪=⎨⎪=⎩，∴△ABC ≌△BAD （SSS ）．在y ＝x 2﹣2x ﹣3中，令x ＝0，得y ＝﹣3，则C （0，﹣3），根据C 点、D 点关于x ＝1对称，则D 点坐标为（2，-3）．【点睛】本题考查了待定系数法求二次函数解析式和全等三角形的判定，解题关键是熟练运用待定系数法求解析式，根据二次函数的对称性解决问题．22．（1）-5；（2）①m =322-，m =222+，m =22-②最大值为3，最小值为-27【分析】（1）先得到2y ax =-的相关函数，再将点A 代入计算即可；（2）①写出二次函数2283y x x =-+-的相关函数，再代入计算； ②根据二次函数的最大值和最小值的求法解答．【详解】解：（1）2y ax =-的相关函数为2(0)2(0)ax x y ax x -+≥⎧=⎨-<⎩， 将(1,3)A -代入2y ax =-，得5a =-； （2）①二次函数2283y x x =-+-的相关函数为22283(0)283(0)x x x y x x x ⎧-+≥=⎨-+-<⎩，当0m <时，将(,4)B m -代入2283y x x =-+-，得：m =22+（舍去）或m =22-， 当0m ≥时，将(,4)B m -代入2283y x x =-+，得：m =22+m =22-，∴m =22-或m =22+或m =22- ②当20x -≤<时，2283y x x =-+-，抛物线的对称轴为2x =，此时y 随x 的增大而增大，∴此时273y -≤<-，当03x ≤≤时，函数2283y x x =-+，抛物线的对称轴为2x =，当2x =有最小值，最小值为-5，当0x =时，有最大值，最大值3y =，∴当23x -≤≤时，函数2283y x x =-+-的相关函数的最大值为3，最小值为-27．【点睛】本题考查的是互为相关函数的定义，掌握二次函数的性质、二次函数与一元二次方程的关系是解题的关键．23．（1）见解析；（2）()2,3-，21x -≤≤【分析】（1）利用五点法作出二次函数的图像，然后令x=0求出A 点坐标即可；（2）将两个函数联立形成新的一元二次方程，然后求解C 点坐标，最后利用图像判断x 的取值范围即可．【详解】（1）由题意得：1由上图得A 点坐标为()3,0-；（2）由题意得：2123x x x -+=--+，解得12x =-，21x =，当2x =-时，()213y =--+=，∴C 点坐标为()2,3-，由上图得，当y 1≥y 2时，21x -≤≤．【点睛】本题考查了二次函数的图像和性质，重点是根据五点法作出二次函数的图像，然后利用数形结合思想进行判断．24．（1）22y x x =-++；（2）（12，-3）或（12，2） 【分析】（1）利用旋转的性质得出A′（-1，0），B′（0，2），再利用待定系数法求二次函数解析式即可；（2）分AQ 是斜边、BQ 是斜边两种情况，利用勾股定理分别求解即可．【详解】解：（1）线段AB 绕原点O 逆时针旋转90°，得到线段A B ''，又A （0，1），B （2，0），∴A′（-1，0），B′（0，2），∵A′（-1，0），B′（0，2），B （2，0），设抛物线的解析式为：y=a （x+1）（x-2）将B′（0，2）代入得出：2=a （0+1）（0-2），解得：a=-1，故满足条件的抛物线的解析式为y=-（x+1）（x-2）=-x 2+x+2；（2）由抛物线的表达式知，函数的对称轴为x=12，故设点Q （12，m ），则()222112AQ m ⎛⎫=+- ⎪⎝⎭，222122BQ m ⎛⎫=-+ ⎪⎝⎭，AB 2=22+1=5， 当AQ 是斜边时， 则()22221112522m m ⎛⎫⎛⎫+-=-++ ⎪ ⎪⎝⎭⎝⎭， 解得m=-3，当BQ 是斜边时，()22221115222m m ⎛⎫⎛⎫+-+=-+ ⎪ ⎪⎝⎭⎝⎭， 解得m=2，故点Q 的坐标为（12，-3）或（12，2）． 【点睛】本题主要考查了待定系数法求二次函数的解析式，二次函数的性质，坐标和图形的变换-旋转，其中（2），利用勾股定理得出方程求出m 是解题关键．25．（1）顶点坐标为()1,0-；（2）2n <-【分析】（1）利用配方法将二次函数解析式变形为顶点式，再利用图象与x 轴有且只有一个公共点，则顶点的纵坐标为0，故函数图象的顶点坐标为（-1，0），（2）将n ，n+2代入二次函数解析式即可得出n 的取值范围．【详解】解：（1）()22211y x x m x m =++=++-，对称轴1x =-∵与x 轴有且只有一个公共点，∴顶点的纵坐标为0．∴函数图象的顶点坐标为()1,0-（2）∵()1,P n y ，()22,Q n y +是该二次函数的图象上的两点，且12y y >，()()22212221n n n n ++>++++，化简整理得，480n +<，∴2n <-，∴实数n 的取值范围是2n <-．【点睛】本题考查了二次函数的性质及解不等式，利用数形结合思想解题是关键．26．矩形猪舍的长、宽分别为12米、8米时，猪舍的面积最大，最大面积是96平方米．【分析】设猪舍的宽为m x ，则长为(2721)m x -+，由题意可得2(2721)2(7)98y x x x =-+=--+，然后再根据二次函数的性质进行求最大值即可；【详解】设猪舍的宽为m x ，则长为(2721)m x -+，由题意得2(2721)2(7)98y x x x =-+=--+，对称轴为7x =， 272112x -+≤，27210x -+>，814x ∴≤<，在22(7)98y x =--+中，∵20-<，∴在对称轴右侧y 随着x 的增大而减小，所以当8x =米时，即矩形猪舍的长、宽分别为12米、8米时，猪舍的面积最大，最大面积是96平方米．【点睛】本题考查了二次函数的应用，矩形的面积公式的运用及二次函数的性质，解答时寻找题目的等量关系是关键；。

2024北师大版数学九年级下册2.3.2《确定二次函数的表达式》教学设计一. 教材分析《确定二次函数的表达式》是北师大版数学九年级下册第2章3.2节的内容。

本节课主要让学生掌握二次函数的通用形式，了解二次函数的各个系数与函数图象的关系，为后续学习二次函数的性质打下基础。

教材通过实例引导学生从实际问题中抽象出二次函数模型，进一步探究二次函数的性质。

二. 学情分析九年级的学生已经学习了函数的基本概念，对一次函数、二次函数有一定的了解。

但学生在确定二次函数表达式方面存在困难，难以把握二次函数的各个系数与函数图象的关系。

因此，在教学过程中，教师需要引导学生从实际问题中抽象出二次函数模型，并通过观察、操作、猜想、验证等方法，让学生体会二次函数的性质。

三. 教学目标1.让学生掌握二次函数的通用形式；2.使学生了解二次函数的各个系数与函数图象的关系；3.培养学生解决实际问题的能力；4.引导学生运用数形结合的方法探究二次函数的性质。

四. 教学重难点1.重点：二次函数的通用形式，二次函数的各个系数与函数图象的关系；2.难点：确定二次函数表达式，二次函数的性质。

五. 教学方法1.情境教学法：通过实际问题引出二次函数模型，激发学生兴趣；2.观察法：让学生观察二次函数图象，发现其性质；3.操作法：让学生动手操作，验证二次函数的性质；4.讨论法：分组讨论，培养学生的合作能力。

六. 教学准备1.课件：制作课件，展示二次函数的图象和性质；2.练习题：准备一些有关二次函数的练习题，巩固所学知识；3.板书：准备黑板，书写关键知识点。

七. 教学过程1.导入（5分钟）教师通过展示一个实际问题，引导学生从实际问题中抽象出二次函数模型。

例如：抛物线与x轴相交于A、B两点，且AB=2，求抛物线的解析式。

2.呈现（10分钟）教师展示二次函数的图象，让学生观察并描述二次函数的性质。

引导学生关注二次函数的顶点、开口方向、对称轴等关键点。

3.操练（10分钟）教师引导学生分组讨论，让学生动手操作，验证二次函数的性质。

确定二次函数的表达式一、选择题1．若二次函数y=x2+bx-2的图象与x轴的一个交点为（1，0），则该二次函数的表达式为（）A．y=x2-2x B．y=x2+x-1 C．y=x2+x-2 D．y=x2-x-22．若二次函数的图象经过点（1，10），顶点坐标为（-1，-2），则此二次函数的表达式为（）A．y=3x2+6x+1 B．y=3x2+6x-1 C．y=3x2-6x+1 D．y=-3x2-6x+1 3．如图，抛物线的函数表达式是（）A．y=x2-x+2 B．y=x2+x+2 C．y=-x2-x+2 D．y=-x2+x+2 4．若y=ax2+bx+c，则由表格某某息可知y与x之间的函数表达式是（）A．y=x2-4x+3 B．．y=x2-4x+8 5．已知二次函数y=x2+bx+c，若b+c=0，则它的图象一定过点（）A．（-1，-1）B．（1，-1） C．（-1，1）D．（1，1）二、填空题6．在二次函数y=x2+bx+c中，函数y与自变量x的部分对应值如下表，则m的值为________．7．若抛物线y=ax2+bx+c的顶点是A（2，1），且经过点B（1，0），则此抛物线的表达式为___________．8．如果一条抛物线的形状与抛物线y=-x2+2的形状相同，且顶点坐标是（4，-2），那么它的函数表达式是__________．9．二次函数的图象如图，则其表达式为__________．10．如果抛物线经过A（-1，-6），B（1，-2），C（2，3）三点，那么抛物线的函数表达式为__________．三、解答题11．如图，已知抛物线y=x2+bx+c的顶点坐标为M（0，-1），与x轴交于A，B两点．（1）求抛物线的函数表达式；（2）判断△MAB的形状，并说明理由．12．如图，一拱桥的截面呈抛物线形状，拱桥两端点与水面的距离都是1 m，拱桥的跨度为10 m，拱桥与水面的最大距离是5 m，桥洞两侧壁上各有一盏距离水面4 m的景观灯．（1）建立适当的直角坐标系并求出抛物线对应的函数表达式；（2）求两盏景观灯之间的水平距离．13．如图，已知二次函数y=x2+mx+n的图象经过点P（-3，1），对称轴是经过点（-1，0）且平行于y轴的直线．（1）求m，n的值；（2）若一次函数y=kx+b的图象经过点P，与x轴相交于点A，与二次函数的图象相交于另一点B，点B在点P的右侧，PA：PB=1：5，求一次函数的表达式．14．已知二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）的图象经过A，B，C，D四个点，其中横坐标x与纵坐标y的对应值如下表：求：（1（2）△ABD的面积．15．如图，已知抛物线y=ax2+bx+c（a≠0）经过A（-1，0），B（3，0），C（0，-3）三点，直线l是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设P是直线l上的一个动点，当点P到点A，B的距离之和最小时，求点P的坐标．16．如图，已知抛物线y=x2+bx+c经过A（-1，0），B（3，0）两点．（1）求抛物线的表达式和顶点坐标；（2）当0<x<3时，求y的取值X围；（3）P为抛物线上一点，若S△PAB =10，求出此时点P的坐标．参考答案一、1．C 2．A 3．D 4．A 5．D二、6．-1 7．y=-x2+4x-3 8．y=（x-4）2-2或y=-（x-4）2-29．y=-x2+2x+3 10．y=x2+2x-5三、11．解：（1）∵在抛物线的函数表达式中二次项系数为1，且顶点为M（0，-1），∴其函数表达式为y=x2-1．（2）△MAB是等腰直角三角形．理由如下：当y=0时，x2-1=0，∴x=±1．∵点M的坐标为（0，-1），∴OA=OB=OM，∴∠OAM=∠OMA=∠OBM=∠OMB=45°，∴∠AMB=90°，∴△MAB是直角三角形，且MA=MB，∴△MAB是等腰直角三角形．12．解：（1）答案不唯一，如建立如图的平面直角坐标系．由题意知，抛物线的顶点坐标为（5，5），与y轴的交点坐标是（0，1）．设抛物线对应的函数表达式是y=a（x-5）2+5．把（0，1）代入y=a（x-5）2+5，得a=-，∴y=-（x-5）2+5（0≤x≤10）．（2）由题意知，两盏景观灯的纵坐标都是4，令4=-（x-5）2+5，∴425（x-5）2=1，∴x1=，x2=．∴两盏景观灯之间的水平距离为-=5（m）．13．解：（1）∵抛物线的对称轴是经过点（-1，0）且平行于y轴的直线，∴-=-1，解得m=2．∵二次函数y=x2+mx+n的图象经过点P（-3，1），∴9-3m+n=1，∴n=3m-8=-2．（2）∵m=2，n=-2，∴二次函数的表达式为y=x2+2x-2．如图，分别过点P，B作PC⊥x轴于点C，BD⊥x轴于点D，则PC∥BD，∴．∵点P的坐标为（-3，1），∴PC=1．∵PA：PB=1：5，∴，∴BD=6，∴点B的纵坐标为6．令6=x2+2x-2，解得x1=2，x2=-4（舍去），∴点B的坐标为（2，6）．∴解得∴一次函数的表达式为y=x+4．14．解：（1）把A，B，C三点的坐标分别代入y=ax2+bx+c，得解得所以二次函数的表达式为y=-x2+3x+3．（2）S△ABD =×3×4=6．15．解：（1）分别将A（-1，0），B（3，0），C（0，-3）代入y=ax2+bx+c，得解得∴抛物线的函数关系式为y=x2-2x-3．（2）当点P在x轴上时，P，A，B三点在一条直线上，则点P到点A，B的距离之和最小，此时点P的横坐标x=-=1．∴点P的坐标为（1，0）．16．解：（1）把A（-1，0），B（3，0）分别代入y=x2+bx+c，得解得∴抛物线的表达式为y=x2-2x-3．∵y=x2-2x-3=（x-1）2-4，∴抛物线的顶点坐标为（1，-4）．（2）由图象可知，当0<x<3时，-4≤y<0．（3）∵A（-1，0），B（3，0），∴AB=4．设P（x，y），则S△PAB =AB·|y|=2|y|=10，∴|y|=5，∴y=±5．①当y=5时，x2-2x-3=5，解得x1=-2，x2=4，此时点P的坐标为（-2，5）或（4，5）．②当y=-5时，x2-2x-3=-5，方程无实数解．综上所述，点P的坐标为（-2，5）或（4，5）．。

2022--2023学年北师大版九年级数学下册《2.3确定二次函数的表达式》同步达标测试题（附答案）一．选择题（共8小题，满分32分）1．将二次函数y＝x2﹣4x+8转化为y＝a（x﹣m）2+k的形式，其结果为（）A．y＝（x﹣2）2+4B．y＝（x+4）2+4C．y＝（x﹣4）2+8D．y＝（x﹣2）2﹣4 2．一抛物线的形状、开口方向与抛物线相同，顶点为（﹣2，1），则此抛物线的解析式为（）A．B．C．D．3．已知二次函数的图象经过（0，0），（3，0），（1，﹣4）三点，则该函数的解析式为（）A．y＝x2﹣3x B．y＝2x2﹣3x C．y＝2x2﹣6x D．y＝x2﹣6x4．已知抛物线y＝x2+bx+c的顶点坐标为（1，3），则抛物线对应的函数解析式为（）A．y＝x2﹣2x+4B．y＝x2﹣2x﹣3C．y＝﹣x2+2x+1D．y＝x2﹣2x+1 5．已知抛物线的顶点坐标是（2，﹣1），且与y轴交于点（0，3），这个抛物线的表达式是（）A．y＝x²﹣4x+3B．y＝x²+4x+3C．y＝x²+4x﹣1D．y＝x²﹣4x﹣1 6．如图，若抛物线y＝ax2﹣2x+a2﹣1经过原点，则抛物线的解析式为（）A．y＝﹣x2﹣2x B．y＝x2﹣2xC．y＝﹣x2﹣2x+1D．y＝﹣x2﹣2x或y＝x2﹣2x7．设函数y＝a（x﹣h）2+k（a，h，k是实数，a≠0），当x＝1时，y＝2；当x＝5时，y＝6，以下判断正确的是（）A．若h＝2，则a＜0B．若h＝4，则a＞0C．若h＝6，则a＜0D．若h＝8，则a＞08．已知某抛物线与二次函数y＝5x2的图象的开口大小相同，开口方向相反，且顶点坐标为（﹣1，2021），则该抛物线对应的函数表达式为（）A．y＝﹣5（x﹣1）2+2021B．y＝5（x﹣1）2+2021C．y＝﹣5（x+1）2+2021D．y＝5（x+1）2+2021二．填空题（共8小题，满分32分）9．小聪在画一个二次函数的图象时，列出了下面几组y与x的对应值：x…012345…y…50﹣3﹣4﹣30…该二次函数的解析式是．10．顶点为（﹣6，0），开口向下，形状与函数y＝x2的图象相同的抛物线的表达式是．11．二次函数y＝x2+bx+c的图象经过点（1，0）和（3，0），则其函数解析式为．12．已知某二次函数y＝x2+bx+c过点A（1，0），B（﹣3，0），则此二次函数的关系式是，若在此抛物线上存在一点P，使△ABP面积为8，则点P的坐标是．13．已知抛物线的顶点在原点，对称轴为y轴，且经过点（﹣1，﹣2），则抛物线的表达式为．14．二次函数与y轴的交点到原点的距离为8，它的顶点坐标为（﹣1，2），那么它的解析式为．15．若抛物线y＝ax2+bx+c（a≠0）与抛物线y＝2x2﹣4x﹣1的顶点重合，且与y轴的交点的坐标为（0，1），则抛物线y＝ax2+bx+c（a≠0）的表达式是．16．已知：二次函数y＝ax2+bx+c中的x、y满足下表：x﹣2﹣11347y﹣5040m﹣36（1）m的值为；（2）此函数的解析式为；（3）若0＜x＜4时，则y的取值范围为．三．解答题（共6小题，满分56分）17．已知抛物线y＝x2+bx+c的图象经过A（﹣1，12）、B（0，5）．（1）求抛物线解析式；（2）试判断该二次函数的图象是否经过点（2，3）．18．已知抛物线y＝ax2+bx﹣3（a，b是常数，a≠0）经过A（﹣1，﹣2），B（1，﹣6）．（1）求抛物线y＝ax2+bx﹣3的函数解析式；（2）抛物线有两点M（2，y1）、N（m，y2），当y1＜y2时，求m的取值范围．19．如图，在平面直角坐标系中，已知抛物线y＝ax2+bx+4（a≠0）经过点A（﹣2，0）和点B（4，0）．（1）求这条抛物线所对应的函数解析式；（2）点P为该抛物线上一点（不与点C重合），直线CP将△ABC的面积分成2：1两部分，求点P的坐标．20．抛物线的顶点坐标为（2，﹣1），抛物线又经过点（1，0）．（1）求抛物线的解析式；（2）在图中画出这条抛物线；（3）根据图象回答，当y＞3时，自变量x的取值范围．21．如图，抛物线y＝ax2+2ax+c经过点A（2，0），B（﹣2，4）．（1）求抛物线的解析式；（2）若函数y＝ax2+2ax+c在m≤x≤m+2时有最大值为4，求m的值；（3）点M在直线AB上方的抛物线上运动，当△ABM的面积最大时，求点M的坐标．22．如图，已知抛物线过点O（0，0），A（5，﹣5），且它的对称轴为直线x＝2．（1）求此抛物线的表达式；（2）若点B是抛物线对称轴上的一点，且点B在第四象限．①当△OAB的面积为10时，求B的坐标；②点P是抛物线上的动点，当P A﹣PB的值最大时，求P的坐标以及P A﹣PB的最大值．参考答案一．选择题（共8小题，满分32分）1．解：y＝x2﹣4x+8＝x2﹣4x+4+4＝（x﹣2）2+4，故选：A．2．解：∵抛物线的形状、开口方向与抛物线相同，∴a＝，∵顶点为（﹣2，1），∴抛物线解析式为y＝（x+2）2+1．故选：C．3．解：设这个二次函数的解析式是y＝ax（x﹣3）（a≠0），把（1，﹣4）代入得﹣4＝﹣2a，解得a＝2；所以该函数的解析式为：y＝2x（x﹣3）＝2x2﹣6x．故选：C．4．解：∵抛物线y＝x2+bx+c的顶点坐标为（1，3），∴抛物线解析式为y＝（x﹣1）2+3，即y＝x2﹣2x+4．故选：A．5．解：∵抛物线的顶点坐标为（2，﹣1）∴设抛物线的解析式为y＝a（x﹣2）2﹣1（a≠0），把（0，3）代入得：4a﹣1＝3，解得，a＝1．所以，这条抛物线的解析式为：y＝（x﹣2）2﹣1＝x2﹣4x+3．故选：A．6．解：把（0，0）代入y＝ax2﹣2x+a2﹣1得，0＝a2﹣1，∴a＝±1，∵抛物线开口向下，∴抛物线的解析式为y＝﹣x2﹣2x，故选：A．7．解：当x＝1时，y＝2；当x＝5时，y＝6；代入函数式得：，∴a（5﹣h）2﹣a（1﹣h）2＝4，整理得：a（6﹣2h）＝1，若h＝2，则a＝，故A错误；若h＝4，则a＝﹣，故B错误；若h＝6，则a＝﹣，故C正确；若h＝8，则a＝﹣，故D错误；故选：C．8．解：∵抛物线的顶点坐标为（﹣1，2021），∴抛物线的解析式为y＝a（x+1）2+2021，∵抛物线y＝a（x+1）2+2021二次函数y＝5x2的图象的开口大小相同，开口方向相反，∴a＝﹣5，∴抛物线的解析式为y＝﹣5（x+1）2+2021．故选：C．二．填空题（共8小题，满分32分）9．解：由表格数据结合二次函数图象对称性可得图象顶点为（3，﹣4），设二次函数的表达式为y＝a（x﹣3）2﹣4（a≠0），将（1，0）代入得4a﹣4＝0，解得a＝1，∴该二次函数的表达式为y＝（x﹣3）2﹣4（或y＝x2﹣6x+5）．10．解：设所求的抛物线的关系式为y＝a（x﹣h）2+k，∵顶点为（﹣6，0），∴h＝﹣6，k＝0，又∵开口向下，形状与函数y＝x2的图象相同，∴a＝﹣，∴抛物线的关系式为：y＝﹣（x+6）2，11．解：∵二次函数y＝x2+bx+c的图象经过点（1，0）和（3，0），∴二次函数为y＝（x﹣1）（x﹣3）＝x2﹣4x+3，故答案为：y＝x2﹣4x+3．12．解：将点A（1，0），B（﹣3，0）代入y＝x2+bx+c中，可得，解得，∴y＝x2+2x﹣3，设P（m，m2+2m﹣3），∵AB＝4，∴S△ABP＝×AB×y P＝×4×|m2+2m﹣3|＝8，∴|m2+2m﹣3|＝4，∴m2+2m﹣3＝4或m2+2m﹣3＝﹣4，解得m＝﹣1±2或m＝﹣1，∴P（﹣1+2，4）或P（﹣1﹣2，4）或P（﹣1，﹣4），故答案为：y＝x2+2x﹣3；（﹣1+2，4）或（﹣1﹣2，4）或（﹣1，﹣4）．13．解：根据题意设抛物线解析式为y＝ax2，将x＝﹣1，y＝﹣2代入得：﹣2＝a，则抛物线解析式为y＝﹣2x2．故答案为：y＝﹣2x2．14．解：∵二次函数的图象顶点坐标为（﹣1，2），∴设这个二次函数的解析式y＝a（x+1）2+2（a≠0），∵二次函数的图象与y轴的交点到原点的距离是8，∴交点坐标为（0，8）或（0，﹣8），把（0，8）代入y＝a（x+1）2+2，得8＝a+2，解得a＝6，则这个二次函数的解析式y＝6（x+1）2+2；把（0，﹣8）代入y＝a（x+1）2+2，得﹣8＝a+2，解得a＝﹣10，则这个二次函数的解析式y＝﹣10（x+1）2+2；故答案为：y＝6（x+1）2+2或y＝﹣10（x+1）2+2．15．解：∵y＝2x2﹣4x﹣1＝2（x﹣1）2﹣3，∴抛物线y＝2x2﹣4x﹣1的顶点坐标为（1，﹣3），∵抛物线y＝ax2+bx+c与抛物线y＝2x2﹣4x﹣1的顶点重合，∴抛物线y＝ax2+bx+c的顶点坐标为（1，﹣3），∴设此抛物线为y＝a（x﹣1）2﹣3，∵与y轴的交点的坐标为（0，1），∴1＝a﹣3，解得a＝4，∴此抛物线为y＝4（x﹣1）2﹣3＝4x2﹣8x+1，故答案为：y＝4x2﹣8x+1．16．解：（1）由图中表格可知，二次函数y＝ax2+bx+c的图象关于直线x＝1对称，且（4，m）与（﹣2，﹣5）关于直线x＝1对称，∴m＝﹣5；故答案为：﹣5；（2）由二次函数y＝ax2+bx+c的图象过（﹣1，0），（3，0），设函数的解析式为y＝a（x+1）（x﹣3），将（1，4）代入得：4＝a×2×（﹣2），解得a＝﹣1，∴y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3，故答案为：y＝﹣x2+2x+3；（3）∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴当x＝1时，y取最大值4，∵1﹣0＜4﹣1，∴x＝4时，y取最小值﹣（4﹣1）2+4＝﹣5，∴0＜x＜4时，y的取值范围为是﹣5＜y≤4；故答案为：﹣5＜y≤4．三．解答题（共6小题，满分56分）17．解：（1）∵抛物线y＝x2+bx+c的图象经过A（﹣1，12），B（0，5）．∴，解得，∴二次函数解析式为y＝x2﹣6x+5；（2）当x＝2时，y＝x2﹣6x+5＝4﹣12+5＝﹣3≠3，∴该二次函数的图象不经过点（2，3）．18．解：（1）把A（﹣1，﹣2），B（1，﹣6）代入y＝ax2+bx﹣3得，解得，∴抛物线的关系式为y＝﹣x2﹣2x﹣3；（2）∵y＝﹣x2﹣2x﹣3，∴抛物线开口向下，对称轴直线x＝﹣＝﹣1，∴由图取抛物线上点Q，使Q与N关于对称轴x＝﹣1对称，∴点M（2，y1）关于对称轴x＝﹣1的对称点为（﹣4，y1），又∵N（m，y2）在抛物线图象上的点，且y1＜y2，∴﹣4＜m＜2．19．解：（1）设抛物线的表达式为y＝a（x﹣x1）（x﹣x2），则y＝a（x+2）（x﹣4）＝ax2﹣2ax﹣8a，即﹣8a＝4，解得a＝﹣，故抛物线的表达式为y＝﹣x2+x+4；（2）由点A、B的坐标知，OB＝2OA，故CO将△ABC的面积分成2：1两部分，此时，点P不在抛物线上；如图1，当BH＝AB＝2时，CH将△ABC的面积分成2：1两部分，即点H的坐标为（2，0），则CH和抛物线的交点即为点P，由点C、H的坐标得，直线CH的表达式为y＝﹣2x+4，联立，解得或，故点P的坐标为（6，﹣8）．20．解：（1）设抛物线的解析式为y＝a（x﹣2）2﹣1，将点（1，0）代入，得a﹣1＝0．解得a＝1，∴抛物线的解析式为y＝（x﹣2）2﹣1，（2）∵y＝（x﹣2）2﹣1＝x2﹣4x+3，∴抛物线与y轴的交点为（0，3），其关于对称轴的对称点为（4，3），令y＝0，则x2﹣4x+3＝0，解得x＝1或3，∴抛物线与x轴的交点为（1，0），（3，0），画出函数图象如下：（3）由函数图象知，当y＞3时，自变量x的取值范围是x＜0或x＞4．21．解：（1）∵抛物线y＝ax2+2ax+c经过点A（2，0），B（﹣2，4），∴，解得，∴抛物线的解析式为y＝﹣x2﹣x+4；（2）∵y＝﹣x2﹣x+4，∴抛物线开口向下，对称轴x＝﹣＝﹣1，∵m≤x≤m+2时，y有最大值4，∴当y＝4时，有﹣x2﹣x+4＝4，∴x＝0或x＝﹣2，①在x＝﹣1左侧，y随x的增大而增大，∴x＝m+2＝﹣2时，y有最大值4，②在对称轴x＝﹣1右侧，y随x最大而减小，∴x＝m＝0时，y有最大值4；综上所述：m＝﹣4或m＝0；（3）过点M作MG∥y轴交直线AB于点G，设直线AB的解析式为y＝kx+b，∴，解得，∴y＝﹣x+2，设M（m，﹣m2﹣m+4），则G（m，﹣m+2），∴MG＝﹣m2+2，∴S△ABM＝×4×（﹣m2+2）＝﹣m2+4，∴当m＝0时，△ABM的面积最大，此时M（0，4）．22．解：（1）∵抛物线过点O（0，0），A（5，﹣5），且它的对称轴为x＝2，∴抛物线与x轴的另一个交点坐标为（4，0），设抛物线解析式为y＝ax（x﹣4），把A（5，﹣5）代入，得5a＝﹣5，解得：a＝﹣1，∴y＝﹣x（x﹣4）＝﹣x2+4x，故此抛物线的解析式为y＝﹣x2+4x；（2）①∵点B是抛物线对称轴上的一点，且点B在第四象限，∴设B（2，m）（m＜0），设直线OA的解析式为y＝kx，解得：k＝﹣1，∴直线OA的解析式为y＝﹣x，设直线OA与抛物线对称轴交于点H，则H（2，﹣2），∴BH＝﹣2﹣m，∵S△OAB＝10，∴×（﹣2﹣m）×5＝10，解得：m＝﹣6，∴点B的坐标为（2，﹣6）；②设直线AB的解析式为y＝cx+d，把A（5，﹣5），B（2，﹣6）代入得：，，解得：，∴直线AB的解析式为y＝x﹣，如图2，当P A﹣PB的值最大时，A、B、P在同一条直线上，∵P是抛物线上的动点，∴，解得：或，∴P（﹣，﹣）．∵AB＝＝，∴P A﹣PB的最大值为．。

北师大版九年级数学下册《2.3 确定二次函数的表达式》练习题-带答案学校:___________班级：___________姓名：___________考号：___________一、填空题1．用配方法把二次函数y =2x 2+3x +1写成y =a(x +m)2+k 的形式_____．2．已知抛物线的顶点为（1，﹣1），且过点（2，1），求这个函数的表达式为 ．3.已知抛物线y ＝ax 2＋bx ＋c (a ≠0)的对称轴为x ＝1，且抛物线经过A(－1，0)，B(0，－3)两点，则这条抛物线所对应的函数关系式为________________．4．已知二次函数的图象经过原点及点（-21，41），且图象与x 轴的负半轴的交点到原点的距离为1，则该二次函数的解析式为 ．5． 若抛物线y =x 2−(m −3)x +2的对称轴为y 轴，则m =________．6．将二次函数y ＝x 2﹣8x +3化为y ＝a （x ﹣m ）2+k 的形式是 ．7．已知二次函数y ＝－12x 2＋bx ＋c 的图象经过A (2，0)，B (0，－6)两点，则这个二次函数的解析式为_________________．8．把y ＝x 2﹣6x +4配方成y ＝a （x ﹣h ）2+k 的形式是 ．9．将抛物线y =x 2向左平移4个单位后，再向下平移2个单位， 则此时抛物线的解析式是________．10．如图，在平面直角坐标系xOy 中，点A （﹣2，﹣2），B （0，3），C （3，3），D （4，﹣2），y 是关于x 的二次函数，抛物线y 1经过点A ，B ，C ，抛物线y 2经过点B ，C ，D ，抛物线y 3经过点A ，B ，D ，抛物线y 4经过点A ，C ，D ．下列判断：①四条抛物线的开口方向均向下；②当x ＜0时至少有一条抛物线表达式中的y 均随x 的增大而减小；③抛物线y 1的顶点在抛物线y 2顶点的上方；④抛物线y 4与y 轴的交点在点B 的上方．所有正确结论的序号为 ．二、选择题11．与抛物线y＝﹣x2+1的顶点相同、形状相同且开口方向相反的抛物线所对应的函数表达式为（）A．y＝﹣x2B．y＝x2﹣1C．y＝﹣x2﹣1D．y＝x2+1 12．一个二次函数的图象过（﹣1，5），（1，1）和（3，5）三个点，则这个二次函数的关系式为（）A．y＝﹣x2﹣2x+2B．y＝x2﹣2x+2C．y＝x2﹣2x+1D．y＝x2﹣2x﹣2 13．若所求的二次函数图象与抛物线y=2x2−4x−1有相同的顶点，并且在对称轴的左侧，y随x的增大而增大，在对称轴的右侧，y随x的增大而减小，则所求二次函数的解析式为（）A．y=−x2+2x+4B．y=−ax2−2ax−3(a>0)C．y=−2x2−4x−5D．y=ax2−2ax+a−3(a<0) 14．如图所示，抛物线的函数表达式是()A．y＝12x2－x＋4 B．y＝－12x2－x＋4C．y＝12x2＋x＋4 D．y＝－12x2＋x＋415.二次函数y=2x2−12x+13经过配方化成y=a(x−ℎ)2+k的形式是（）A．y=2(x+3)2+5B．y=2(x+3)2−5C．y=2(x−3)2+5D．y=2(x−3)2−516．二次函数y＝﹣x2﹣2x+1配方后，结果正确的是（）A．y＝﹣（x+1）2+2B．y＝﹣（x﹣1）2+2C．y＝﹣（x+1）2﹣2D．y＝﹣（x﹣1）2﹣217．二次函数的图象经过(0, 3)，(−2, −5)，(1, 4)三点，则它的解析式为（）A．y=x2+6x+3B．y=−3x2−2x+3C．y=2x2+8x+3D．y=−x2+2x+318．抛物线的图象如图所示，根据图象可知，抛物线的解析式可能是()A．y＝x2－x－2 B．y＝－12x2－12x＋2C．y＝－12x2－12x＋1 D．y＝－x2＋x＋2三、解答题19．将下列各二次函数解析式化为y＝a（x﹣h）2+k的形式，并写出顶点坐标．（1）y＝x2﹣6x﹣1 （2）y＝﹣2x2﹣4x﹣6（3）y＝x2+3x+10．20．已知函数y=x2+bx−1的图象经过点(3, 2)．(1)求这个函数的解析式；(2)当x>0时求使y≥2的x的取值范围．参考答案1． y =2(x +34)2−18．2． y ＝2x 2﹣4x +1．3．y ＝x 2－2x －3．12． y =-x 2-x ． 4． 35．y ＝（x ﹣4）2﹣13．6．y ＝－12x 2＋4x －6 7．y ＝（x ﹣3）2﹣5．8．y =（x +4）2-2 （y =x 2+8x +14）． 9．①④．10．D ．12．B ．13．D ．14．D ．15． D ．16．A ．17． D ．18．D ．19．解：（1）y ＝x 2﹣6x ﹣1＝x 2﹣6x +9﹣9﹣1＝（x ﹣3）2﹣10 ∴顶点（ 3，﹣10 ）；（2）y ＝﹣2x 2﹣4x ﹣6＝﹣2（x 2+2x +1﹣1）﹣6＝﹣2（x +1）2﹣4 顶点（﹣1，﹣4 ）；（3）y ＝x 2+3x +10＝（x 2+6x +9﹣9）+10＝（x +3）2+顶点（﹣3， ）． 20． 解：(1)∵函数y =x 2+bx −1的图象经过点(3, 2)∴9+3b −1=2解得：b =−2则函数解析式为y =x 2−2x −1；(2)当x =3时y =2根据二次函数性质当x ≥3时y ≥2则当x >0时使y ≥2的x 的取值范围是x ≥3．。

北师大版数学九年级下册2.3.1《确定二次函数的表达式》说课稿1一. 教材分析北师大版数学九年级下册2.3.1《确定二次函数的表达式》这一节主要介绍了二次函数的表达式以及如何确定二次函数的表达式。

二次函数是中学数学中的重要内容，对于学生来说，掌握二次函数的表达式以及确定方法具有重要意义。

本节课通过实例引导学生掌握待定系数法确定二次函数的表达式，培养学生运用数学知识解决实际问题的能力。

二. 学情分析九年级的学生已经学习了函数、方程等基础知识，对函数的概念有一定的了解。

同时，学生已经掌握了二次函数的一般形式，具备了一定的数学思维能力。

但是，对于如何确定二次函数的表达式，学生可能还存在一定的困惑。

因此，在教学过程中，教师需要关注学生的认知基础，引导学生逐步掌握确定二次函数表达式的方法。

三. 说教学目标1.知识与技能目标：让学生掌握待定系数法确定二次函数的表达式，能运用所学知识解决实际问题。

2.过程与方法目标：通过观察、分析、归纳等数学活动，培养学生运用数学知识解决实际问题的能力。

3.情感态度与价值观目标：激发学生学习数学的兴趣，培养学生的团队合作意识，使学生感受到数学在生活中的应用价值。

四. 说教学重难点1.教学重点：待定系数法确定二次函数的表达式。

2.教学难点：如何引导学生运用待定系数法确定二次函数的表达式，以及如何将实际问题转化为数学问题。

五.说教学方法与手段1.教学方法：采用启发式教学法、案例教学法、小组合作学习法等。

2.教学手段：利用多媒体课件、黑板、粉笔等。

六. 说教学过程1.导入新课：通过复习二次函数的一般形式，引导学生思考如何确定二次函数的表达式。

2.新课讲解：讲解待定系数法确定二次函数的表达式，并通过实例进行分析。

3.课堂互动：学生分组讨论，尝试运用待定系数法确定给定二次函数的表达式。

4.总结提升：教师引导学生总结确定二次函数表达式的步骤，并强调其在实际问题中的应用。

5.课堂练习：布置相关练习题，让学生巩固所学知识。