三角形内角和证明汇总

三角形内角和定理证明
三角形内角和定理是几何学中一个重要的定理，该定理在三角形中描述了三个内角之和为180°。

该定理有很多不同的证明方法，而在本文中，我们将使用向量方法来证明三角形内角和定理。

证明：
假设有ABC三角形，由OA、OB、OC分别表示三边AB 、BC、CA所对应的单位向量，则有：
OA+OB+OC=0
推导：假设OA和OB的夹角为θ ,OA和OC的夹角为φ。

记角度A＝|OA，OB|，C＝|OC，OA|，以及B＝|OB，OC|，
根据内积公式有：
OA·OB = |OA|. |OB|cosθ
代入上式：
OA·OB + OC·OA + OB·OC=(|OA|. |OB| + |OB|. |OC| + |OC|. |OA|)cosθ cosφ cos（180°-θ-φ）
结合此处弦长恒等于两边之和（a²=b²+c²-2bc·cosA）：
结论：由上述推导，OA+OB+OC=0，即A+B+C=180°。

三角形内角和180°证明方法1.如图，证明∠B+∠C+∠BAC=180°证明：过A点作DE∥BC∵DE∥BC∴∠B=∠DAB，∠C=∠EAC（两直线平行，内错角相等）∵D,A,E三点共线∴∠DAE=180°∵∠DAE=∠DAB+∠BAC+∠CAE∴∠DAB+∠BAC+∠CAE=180°∴∠B+∠C+∠BAC=180°2.如图，证明：∠B+∠A+∠ACB=180°证明：过C点作CD∥AB，延长BC交CD于C∵CD∥AB∴∠A=∠ACD（两直线平行，内错角相等）∠B=∠DCE（两直线平行，同位角相等）∵B,C,E三点共线∴∠BCE=180°∵∠BCE=∠ACB+∠ACD+∠DCE∴∠ACB+∠ACD+∠DCE=180°∴∠A+∠B+∠ACB=180°3.如图，证明：∠C+∠BAC+∠B=180°证明：过A点作AD∥BC∵AD∥BC∴∠C=∠ADC（两直线平行，内错角相等）CBDB CDEA∠DAC+∠B=180°（两直线平行，同旁内角互补） ∵∠DAC=∠DAC+∠CAB ∴∠DAC+∠CAB+∠B=180° ∵∠C=∠ADC∴∠C+∠CAB+∠B=180°4.如图，证明：∠BAC+∠C+∠B=180°证明：过A 点作DE ∥BC ，延长AC 、BC 交DE 于A 点∵DE ∥BC∴∠C=∠FDA ，∠B=∠GAE （两直线平行，同位角相等） ∵D,A,E 三点共线 ∴∠DAE=180°∵∠DAE=∠DFA+∠FAG+∠GAE ∴∠DFA+∠FAG+∠GAE=180° ∵·∠GAE=∠BAC （对顶角相等） ∴∠BAC+∠C+∠B=180°5.如图，证明：∠A+∠C+∠B=180° 证明：作直线DE ∥AC ，FE ∥AB 交BC 于E∵DE ∥AC∴∠AFE+∠DEF=180°（两直线平行，同旁内角互补） ∠C=∠DEB （两直线平行，同位角相等） ∵FE ∥AB∴∠AFE+∠A=180°（两直线平行，同旁内角互补） ∠B=∠FEC （两直线平行，同位角相等） ∴∠A=∠DEFBCBCFGBAC E∵B,C,E三点共线∴∠BCE=180°∵∠BCE=∠DEB+∠DEF+∠FEC∴∠DEB+∠DEF+∠FEC =180°∴∠A+∠C+∠B=180°6.如图，证明：∠A+∠B+∠C=180°证明：作DE∥AC，FG∥AB，MN∥BC，都交于点O∵DE∥AC∴∠AFO+∠FOD=180°（两直线平行，同旁内角互补）∵FG∥AB∴∠AFO+∠A=180°（两直线平行，同旁内角互补）∴∠A=∠FOD∵MN∥BC∴∠C=∠FNO∵DE∥AC∴∠FNO=∠DOM（两直线平行，同位角相等）∴∠C=∠DOM∵MN∥BC∴∠B=∠DMO（两直线平行，同位角相等）∵FG∥AB∴∠DMO=∠FON（两直线平行，同位角相等）∴∠B=∠FNO∵M,O,N三点共线∴∠MON=180°∵∠MON=∠DOM+∠DOF+∠FON BCGE∴∠DOF+∠DOM+∠FON=180° ∴∠A+∠B+∠C=180°7. 如图，证明：∠BAC+∠CBA+∠ACB=180° 证明：作DE ∥AC ，FG ∥AB ，MN ∥BC ，都交于点O延长AC 交FG 于点K ，延长AB 到点L ，延长BC 交FG 于点P∵ MN ∥BC∴∠ABC=∠AHN ，∠ACB=∠ANM （两直线平行，同位角相等） ∵ AB ∥FG∴∠AHN=∠FON ，∠BAC=∠AKO （两直线平行，同位角相等）∴∠ABC=∠FON ∵ DE ∥AC ∴∠ANM=∠DOM（两直线平行，同位角相等） ∠OKA=∠DOF（两直线平行，内错角相等） ∴∠ACB=∠DOM ∵ FG ∥AB∴∠BAC=∠OKA （两直线平行，同位角相等） ∴∠BAC=∠DOF ∵ M,O,N 三点共线 ∴∠MON=180°∵∠MON=∠DOM+∠DOF+∠FON ∴∠DOM+∠DOF+∠FON=180° ∴∠BAC+∠CBA+∠ACB=180°CB EFGP。

三角形内角和定理的证明方法
三角形内角和定理又被称为三角形内角的性质，它是指任意三角形的三个内角和等于180度。

证明方法如下：
1. 画出任意三角形ABC，并且在三角形的一边AC上取一点D。

2. 连接BD。

3. 分别求解△ABC和△DBC的三角形内角和。

3.1 对于△ABC，我们知道∠ABC+∠BAC+∠CAB=180度。

3.2 对于△DBC，根据三角形内角和定理，我们知道
∠DBC+∠BDC+∠DCB=180度。

4. 观察△ABC和△DBC的两个内角和中的两个角，即∠ABC 和∠BDC，它们是重叠的，即∠ABC=∠BDC。

5. 将等式∠ABC+∠BAC+∠CAB=180度代入等式
∠DBC+∠BDC+∠DCB=180度，得到
∠BDC+∠BAC+∠CAB=180度。

6. 根据等式∠BDC+∠BAC+∠CAB=180度，我们得到△ABC 和△DBC的三个内角和相等。

7. 根据三角形内角和定理，我们可以得知任意三角形的三个内角和等于180度。

综上所述，这是三角形内角和定理的证明方法。

整理三角形内角和定理的证明方法嘿，咱今儿就来聊聊三角形内角和定理的证明方法，这可有意思啦！
你想想看，三角形那三个角，它们加起来到底为啥就是 180 度呢？
这就好像一个神秘的谜团等着我们去解开。

第一种方法呢，就像是搭积木一样。

我们可以画一个三角形，然后
延长它的一边，再通过平行线的魔力，就能发现一些奇妙的角度关系，顺藤摸瓜就证明出来啦！你说神奇不神奇？
还有一种方法呢，就像是变魔术。

把三角形的三个角剪下来，然后
拼在一起，嘿，你猜怎么着，就拼成了一个平角，那不就正好 180 度嘛！这就像把分散的力量一下子聚集起来了。

再有一种方法，是通过几何图形的巧妙构造。

就好像是建筑师在搭
建一个特别的建筑，用各种线条和角度的组合来证明这个定理。

这需
要我们有一双善于发现的眼睛和灵活的思维，就像在迷宫中找到正确
的道路一样刺激！
咱说三角形内角和定理，那可是几何学里的宝贝呀！它就像一把钥匙，能打开好多知识的大门。

以后遇到和三角形有关的问题，咱就可
以拿出这个定理来，就像将军拿出宝剑一样威风！
你说要是没有这个定理，那我们对三角形的理解得少多少乐趣呀！
它就像星星一样，在数学的天空中闪闪发光。

整理这些证明方法，就像是在整理一个宝藏箱，每一种方法都是一
颗璀璨的宝石。

我们可以慢慢欣赏，慢慢琢磨，感受数学的魅力。

这就是三角形内角和定理的证明方法，是不是很有趣呀？它们就像
是一个个小精灵，在数学的世界里跳跃，等待着我们去发现和探索呢！。

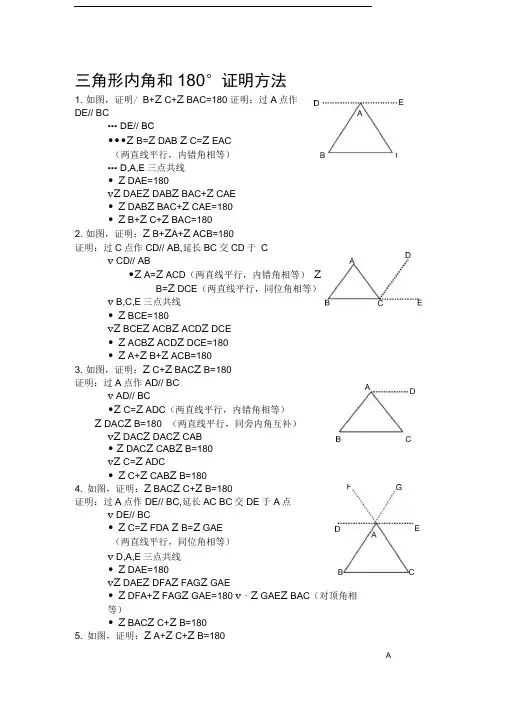
三角形内角和180°证明方法1. 如图，证明/ B+Z C+Z BAC=180 证明：过A点作DE// BC••• DE// BC•••Z B=Z DAB Z C=Z EAC（两直线平行，内错角相等）••• D,A,E三点共线•Z DAE=180vZ DAE Z DAB Z BAC+Z CAE•Z DAB Z BAC+Z CAE=180•Z B+Z C+Z BAC=1802. 如图，证明：Z B+Z A+Z ACB=180证明：过C点作CD// AB,延长BC交CD于 Cv CD// AB•Z A=Z ACD（两直线平行，内错角相等）ZB=Z DCE（两直线平行，同位角相等）v B,C,E三点共线•Z BCE=180vZ BCE Z ACB Z ACD Z DCE•Z ACB Z ACD Z DCE=180•Z A+Z B+Z ACB=1803. 如图，证明：Z C+Z BAC Z B=180°证明：过A点作AD// BCv AD// BC•Z C=Z ADC（两直线平行，内错角相等）Z DAC Z B=180°（两直线平行，同旁内角互补）vZ DAC Z DAC Z CAB• Z DAC Z CAB Z B=180°vZ C=Z ADC•Z C+Z CAB Z B=180°4. 如图，证明：Z BAC Z C+Z B=180°证明：过A点作DE// BC,延长AC BC交DE于A点v DE// BC•Z C=Z FDA Z B=Z GAE（两直线平行，同位角相等）v D,A,E三点共线•Z DAE=180vZ DAE Z DFA Z FAG Z GAE•Z DFA+Z FAG Z GAE=180 v・Z GAE Z BAC（对顶角相等）•Z BAC Z C+Z B=180°5. 如图，证明：Z A+Z C+Z B=180°EEA证明：作直线DE// AC FE// AB交BC于 EA•••DE// AC•••/ AFE+Z DEF=180 （两直线平行，同旁内角互补）/ C=Z DEB（两直线平行，同位角相等）•FE// AB•••/ AFE+/ A=180°（两直线平行，同旁内角互补）Z B=Z FEC（两直线平行，同位角相等）•••/ A=Z DEF•B,C,E三点共线•••Z BCE=180•Z BCE Z DEB Z DEF Z FEC•Z DEB Z DEF Z FEC =180°•Z A+Z C+Z B=180°6. 如图，证明：Z A+Z B+Z C=180 证明：作DE// AC, FG// AB MN/ BC，都交于点O•DE// AC•Z AFO Z FOD=180 （两直线平行，同旁内角互补）•FG// AB•Z AFO Z A=180°（两直线平行，同旁内角互补）•Z A=Z FOD•MN/ BC•Z C=Z FNO（两直线平行，同位角相等）•DE// AC•Z FNO Z DO（两直线平行，同位角相等）•Z C=Z DOM•MN/ BC•Z B=Z DM（两直线平行，同位角相等）•FG// AB•Z DMO Z FON（两直线平行，同位角相等）•Z B=Z FNO•M,O,N三点共线•Z MON=180•Z MON Z DOM Z DOF Z FON•Z DOF Z DOM Z FON=180•Z A+Z B+Z C=1807. 如图，证明：Z BAC Z CBA Z ACB=180证明：作DE// AC, FG// AB MN/ BC，都交于点O延长AC交FG于点K,延长AB到点L,延长BC交FG于点P• MN// BC•Z ABC Z AHN Z ACB Z ANM（两直线平行，同位角相等）•AB // FG•Z AHN Z FON Z BAC Z AKO（两直线平行，同位角相等）•••/ ABC=/ FON••• DE// AC •••/ ANM N DOM（两直线平行，同位角相等）/ OKA N DOF（两直线平行，内错角相等）•••N ACB N DOM••• FG// AB•/ BAC N OKA（两直线平行，同位角相等）•N BAC N DOF••• M,O,N三点共线•N MON=18°vZ MON N DOM N DOF N FON•/ DOM N DOF N FON=180•N BAC N CBA N ACB=180A。

三角形的内角和与外角和关系（基础）知识讲解【学习目标】1．理解三角形内角和定理的证明方法；2．掌握三角形内角和定理及三角形的外角性质；3．能够运用三角形内角和定理及三角形的外角性质进行相关的计算，证明问题.【要点梳理】要点一、三角形的内角和1.三角形内角和定理：三角形的内角和为180°．2.结论：直角三角形的两个锐角互余.要点诠释：应用三角形内角和定理可以解决以下三类问题：①在三角形中已知任意两个角的度数可以求出第三个角的度数；②已知三角形三个内角的关系，可以求出其内角的度数；③求一个三角形中各角之间的关系．要点二、三角形的外角1．定义：三角形的一边与另一边的延长线组成的角叫做三角形的外角．如图，∠ACD是△ABC的一个外角.要点诠释：（1）外角的特征：①顶点在三角形的一个顶点上；②一条边是三角形的一边；③另一条边是三角形某条边的延长线．（2）三角形每个顶点处有两个外角，它们是对顶角．所以三角形共有六个外角，通常每个顶点处取一个外角，因此，我们常说三角形有三个外角．2．性质：（1）三角形的一个外角等于与它不相邻的两个内角的和．（2）三角形的一个外角大于任意一个与它不相邻的内角．要点诠释：三角形内角和定理和三角形外角的性质是求角度及与角有关的推理、证明经常使用的理论依据．另外，在证明角的不等关系时也常想到外角的性质．3.三角形的外角和：三角形的外角和等于360°.要点诠释：因为三角形的每个外角与它相邻的内角是邻补角，由三角形的内角和是180°，可推出三角形的三个外角和是360°．【典型例题】类型一、三角形的内角和1．证明：三角形的内角和为180°.【答案与解析】解：已知：如图，已知△ABC，求证：∠A+∠B+∠C＝180°.证法1：如图1所示，延长BC 到E ，作CD ∥AB ．∵ AB ∥CD （已作），∴ ∠1=∠A （两直线平行，内错角相等），∠B=∠2（两直线平行，同位角相等）．又∵∠ACB+∠1+∠2=180°（平角定义），∴∠ACB+∠A+∠B=180°（等量代换）．证法2：如图2所示，在BC 边上任取一点D ，作DE ∥AB ，交AC 于E ，DF ∥AC ，交AB 于点F ．∵DF ∥AC （已作），∴∠1=∠C （两直线平行，同位角相等），∠2=∠DEC （两直线平行，内错角相等）．∵DE ∥AB （已作）．∴∠3=∠B ，∠DEC=∠A （两直线平行，同位角相等）．∴∠A=∠2（等量代换）．又∵∠1+∠2+∠3=180°（平角定义），∴∠A+∠B+∠C=180°（等量代换）．证法3：如图3所示，过A 点任作直线1l ，过B 点作2l ∥1l ，过C 点作3l ∥1l ，∵1l ∥3l （已作）．∴∠l=∠2（两直线平行，内错角相等）．同理∠3=∠4．又∵1l ∥2l （已作），∴∠5+∠1+∠6+∠4=180°（两直线平行，同旁内角互补）．∴∠5+∠2+∠6+∠3=180°（等量代换）．又∵∠2+∠3=∠ACB ，∴∠BAC+∠ABC+∠ACB=180°（等量代换）．【总结升华】三角形内角和定理的证明方法有很多种，无论哪种证明方法，都是应用的平行线的性质.2.在△ABC 中，已知∠A+∠B ＝80°，∠C ＝2∠B ，试求∠A ，∠B 和∠C 的度数．【思路点拨】题中给出两个条件：∠A+∠B ＝80°，∠C ＝2∠B ，再根据三角形的内角和等于180°，即∠A+∠B+∠C ＝180°就可以求出∠A ，∠B 和∠C 的度数．【答案与解析】解：由∠A+∠B ＝80°及∠A+∠B+∠C ＝180°，知∠C ＝100°．又∵ ∠C ＝2∠B ，∴ ∠B ＝50°．∴ ∠A ＝80°-∠B ＝80°-50°＝30°．【总结升华】解答本题的关键是利用隐含条件∠A+∠B+∠C ＝180°．本题可以设∠B ＝x ，则∠A ＝80°-x ，∠C ＝2x 建立方程求解．【高清课堂：与三角形有关的角 例1、】举一反三：【变式】已知，如图 ，在△ABC 中，∠C=∠ABC=2∠A ，BD 是AC 边上的高，求∠DBC 的度数.【答案】解：已知△ABC中，∠C=∠ABC=2∠A设∠A=x则∠C=∠ABC=2xx+2x+2x=180°解得：x=36°∴∠C=2x=72°在△BDC中， BD是AC边上的高，∴∠BDC=90°∴∠DBC=180°－90°-72°=18°类型二、三角形的外角【高清课堂：与三角形有关的角例2、】3.（1）如图，AB和CD交于点O，求证：∠A＋∠C＝∠B＋∠D ．（2）如图，求证：∠D=∠A＋∠B +∠C．【答案与解析】解：（1）如图，在△AOC中，∠COB是一个外角，由外角的性质可得：∠COB＝∠A＋∠C，同理，在△BOD中，∠COB＝∠B＋∠D，所以∠A＋∠C＝∠B＋∠D．（2）如图，延长线段BD交线段与点E，在△ABE中，∠BEC＝∠A＋∠B ①；在△DCE中，∠BDC＝∠BEC＋∠C ②，将①代入②得，∠BDC＝∠A＋∠B＋∠C，即得证．【总结升华】重要结论：（1）“8”字形图：∠A＋∠C＝∠B＋∠D；（2）“燕尾形图”：∠D=∠A＋∠B +∠C．举一反三：【变式1】如图，AB∥CD，AD和BC相交于点O，∠A＝40°，∠AOB＝75°，则∠C等于（）A、40°B、65°C、75°D、115°【答案】B【变式2】如图，在△ABC中，∠A＝70°，BO，CO分别平分∠ABC和∠ACB，则∠BOC的度数为 .【答案】125°类型三、三角形的内角、外角综合4.如图所示，已知DE分别交△ABC的边AB、AC于D、E，交BC的延长线于F，∠B＝67°，∠ACB＝74°，∠AED＝48°，求∠BDF的度数．【思路点拨】要求∠BDF的度数，应从三角形内角和与三角形的外角出发，若将∠BDF看成△BDF的内角，只需求∠F的度数即可．【答案与解析】解：∵∠CEF＝∠AED＝48°，∠BCA＝∠CEF+∠F，∴∠F＝∠BCA-∠CEF＝74°-48°＝26°，∴∠BDF＝180°-∠B-∠F＝180°-67°-26°＝87°．【总结升华】三角形内角和与外角是进行与角有关的计算或证明的重要工具，本题也可将∠BDF看成△ADE的外角来求解．举一反三：【变式】如图所示，已知△ABC中，P为内角平分线AD、BE、CF的交点，过点P作PG⊥BC 于G，试说明∠BPD与∠CPG的大小关系并说明理由．【答案】解：∠BPD＝∠CPG；理由如下：∵ AD、BE、CF分别是∠BAC、∠ABC、∠ACB的角平分线，∴∠1＝12∠ABC，∠2＝12∠BAC，∠3＝12∠ACB，∴∠1+∠2+∠3＝12(∠ABC+∠BAC+∠ACB)＝90°，又∵∠4＝∠1+∠2，∴∠4+∠3＝90°，又∵ PG⊥BC，∴∠3+∠5＝90°，∴∠4＝∠5，即∠BPD＝∠CPG．。

三角形内角和证明方法三角形内角和是指三角形的三个内角的度数之和，它是三角形最基本的性质之一。

在本文中，我们将介绍一些关于三角形内角和的证明方法。

1.我们可以使用三角形内角和定理来证明三角形内角和的性质。

根据该定理，三角形的内角和等于180度。

证明方法：假设ABC是一个三角形，我们可以作三角形的外接圆O。

连接AO，BO，CO，以及连接AO与BC的垂线OD。

根据外接圆的性质，AO的长度等于半径R，而R为定值。

又因为AO与OD相交，所以AO的垂足D到外接圆的距离等于OD的长度。

由于OD与BC垂直，并且是BC的中线，所以OD的长度等于BC的一半，即OD=BC/2。

根据三角形ABC的内角和定理，∠A+∠B+∠C=180度，而∠A和∠B是三角形的两个锐角，它们可以理解为AO和BO在三角形内角A和B上的倒影，所以∠A和∠B的和等于AO和BO的倒影两个角之和，即∠A+∠B=∠DOA+∠DOB。

同理，∠B+∠C=∠BOC+∠BOA，∠C+∠A=∠COA+∠COD。

因为∠DOA+∠DOB+∠BOC+∠BOA+∠COA+∠COD=360度，而∠A+∠B+∠C=180度，所以∠DOA+∠DOB+∠BOC+∠BOA+∠COA+∠COD-∠A-∠B-∠C=360度-180度=180度。

同理∠DOA+∠COA=180度-∠A-∠C，∠DOB+∠BOA=180度-∠A-∠B，∠BOC+∠COD=180度-∠B-∠C。

将上述等式代入∠A+∠B+∠C=180度，得到：(180度-∠A-∠C)+(180度-∠A-∠B)+(180度-∠B-∠C)=180度。

化简上述等式，可以得到3*180度-2*(∠A+∠B+∠C)=180度，即3*180度=2*(∠A+∠B+∠C)，进一步化简为∠A+∠B+∠C=180度。

证明完毕。

2.另一种证明三角形内角和的方法是使用拓扑学中的欧拉公式。

根据欧拉公式，一个简单多边形的顶点数、边数和面数之间存在着一个关系。

三角形的内角和证明方法1三角形的定义三角形是一个平面图形，由三条线段连接的三个点组成的图形。

三条线段称为三角形的边，连接边的点称为三角形的顶点。

2三角形的内角和三角形的内角和是指三角形内部三个角的角度之和。

在任何三角形中，内角之和总是等于180度（π弧度）。

3三角形内角和的证明方法一种简单的证明三角形内角和等于180度的方法是使用平行线切割定理。

1.从三角形的一个顶点开始，将一条线段作为其中一条边，该线段与另外两边相交于两个点。

2.以顶点为圆心，构造一个小圆，使得该圆与线段相切于顶点，并与另外两边相交于两个点。

3.连接这两个点，构造一条直线，平行于线段。

4.做垂线，将三角形分成两个三角形，一个内角为α，一个内角为β。

5.根据平行线切割定理，α和β相等。

6.重复上述过程，将三角形分成三个三角形。

7.根据平行线切割定理，内角之和等于180度。

4三角形内角和的另一种证明方法另一种证明三角形内角和等于180度的方法是使用三角形的面积。

1.以三角形的一个顶点为圆心，作一个圆。

2.连接圆心与另外两个顶点，形成两个角。

这两个角的度数x和y之和等于360度。

3.构造三角形的高，使之垂直于底边。

4.三角形的面积等于底边乘以高的一半。

5.将三角形旋转180度，使高所在的线段与底边重合。

6.三角形的面积等于底边乘以高的一半。

7.根据三角形的面积公式，两次求得的面积相等，所以底边乘以高的一半也相等。

8.三角形的高可以表示为底边的三角函数（正弦或余弦）。

9.将高表示为底边的三角函数并代入底边乘以高的一半的公式，得到影子公式。

10.影子公式中的角度之和等于180度。

5结论通过平行线切割定理和三角形的面积公式，我们可以证明三角形的内角和等于180度。

这个结论对于解决三角形几何问题非常有用，因为它可以用作许多三角形定理的基础。

三角形内角和证明汇总三角形是平面几何中最简单的多边形之一，它由三条边和三个内角组成。

在这篇文章中，我将汇总三角形内角和的证明，包括三角形内角和等于180度以及其他有关三角形内角和的性质证明。

1.三角形内角和等于180度：三角形的内角和等于180度是三角形基本性质之一、我们可以通过以下两种证明方法证明这个结论。

方法一：利用平行线和内错角的性质证明。

假设ABC是一个三角形，根据平行线和内错角的性质，我们可以得出以下结论：∠ABC+∠BCD=180度同样地，我们可以得到以下两个等式：∠ABC+∠ACB=180度∠BCD+∠ACB=180度综上所述，我们可以得出：∠ABC+∠BCD+∠ACB=180度方法二：利用三角形的外角和等于360度证明。

我们知道一个三角形的外角和等于360度。

假设ABC是一个三角形，由于∠ABC是外角，所以有：∠ABC+∠ACB=180度同样地，我们可以得到以下等式：∠ABC+∠BCD=180度∠ACB+∠BCD=180度综上所述，我们可以得出：∠ABC+∠BCD+∠ACB=180度2.三角形内角和的其他性质：除了内角和等于180度之外，三角形的内角和还具有其他一些性质。

以下是一些相关的证明：性质一：三角形的一个内角大于另外两个内角之和。

假设ABC是一个三角形，我们可以利用反证法证明这个性质。

假设∠ABC<∠ACB+∠BCA。

由于∠ABC是一个内角，所以可以得到以下不等式：∠ABC+∠ACB+∠BCA<∠ACB+∠BCA+∠BCA经简化得：∠ABC+∠ACB+∠BCA<2∠ACB+2∠BCA由于∠ABC<∠ACB+∠BCA，所以2∠ABC<2∠ACB+2∠BCA。

因此，根据三角形内角和等于180度的性质，我们可以得出∠ABC+∠ACB+∠BCA>180度，与假设相矛盾。

综上所述，结论成立。

性质二：三角形的两个内角之和小于180度。

假设ABC是一个三角形，我们可以利用反证法证明这个性质。

三角形内角和三角形是几何学中最基本的图形之一，它由三条线段组成，每个线段都与其他两条线段相连接形成三个内角。

本文将讨论三角形的内角和，并对其性质进行探究。

一、三角形的内角和性质设三角形的三个内角分别为A、B、C，其内角和为180度。

也就是说，A + B + C = 180度。

这个性质被称为三角形内角和定理，是几何学中最基本的性质之一。

二、证明三角形内角和性质要证明三角形内角和为180度，可以通过多种方法进行证明。

本文将介绍两种常用的证明方法。

方法一：三角形内角和与直线平行性质结合在三角形ABC中，延长边AC，分别延长到点D和E上，使得AD和BE与BC平行。

根据平行线性质，∠BED与∠EBC为内错角、∠CAD与∠ACB为内错角。

考虑△ADC，对内角A进行角度求和，则∠CAD + ∠ADC = 180度。

考虑△BEC，对内角B进行角度求和，则∠BED + ∠BEC = 180度。

观察△ADC和△BEC的内角和，有∠CAD + ∠ADC + ∠BED +∠BEC = 360度。

将上述两个等式相减，得到∠CAD + ∠ADC - (∠CAD + ∠ACB) +∠BED + ∠BEC - (∠BEC + ∠ACB) = 360度 - 180度。

化简可得∠ADC - ∠ACB + ∠BED - ∠ACB = 180度。

即有∠ADC + ∠BED = 2∠ACB。

继续化简，得到2∠ACB = 180度，即∠ACB = 90度。

由此可得，三角形ABC中的一个内角为90度。

结合前面提到的三角形内角和定理，可推知三角形的另外两个内角之和也为90度。

所以，三角形的内角和为180度。

方法二：三角形内角和与直线平行性质相结合在三角形ABC中，延长边AC，接下来在边BC的延长线上取一点D，使得AD与AC重合。

根据三角形内角和定理，∠ABC + ∠BAC + ∠BCA = 180度。

在三角形ABC中，AD || BC，根据平行线性质，可知∠ABC +∠ACD = 180度。

三角形内角和证明三角形的内角和是180°是几何学中的基本定理之一、本文将通过使用三角形的几何性质和数学推导，证明三角形内角和定理。

首先，我们需要了解一些三角形的性质：1.三角形的所有内角相加等于180°。

这个定理可以通过将三角形分成两个直角三角形，并利用直角三角形内角和为180°来证明。

2.三角形的补角等于180°。

如果两个角是互补角，则它们的和为180°。

这个性质可以通过绘制两个互补角，然后利用直角三角形的性质来证明。

3.三角形的两个角的和等于第三个角。

这个性质可以通过绘制一个任意三角形，然后观察三个角的关系来证明。

现在，我们开始证明三角形的内角和定理。

假设我们有一个任意的三角形ABC，其中角A的度数为α，角B的度数为β，角C的度数为γ。

我们可以通过将三角形ABC分解成两个互补角形来证明内角和定理。

首先，我们令角A和B为互补角，它们的和为180°。

因此，我们可以得到以下等式：α+β=180°(1)接下来，我们将角B和角C设为互补角，它们的和也为180°。

所以我们有：β+γ=180°(2)我们现在可以解方程（1）和（2）以获得α和γ之间的关系。

首先，我们从方程（1）中解出β：β=180°-α然后，我们将这个值代入到方程（2）中：180°-α+γ=180°通过简化上述等式，我们可以得到：γ=α这意味着角A和角C的度数是相等的。

现在，我们已经知道角A和角C的度数是相等的，我们可以使用三角形的第三个性质来求解角B的度数。

根据三角形的第三个角度性质，我们知道：α+β+γ=180°将α和γ的值代入，我们得到：α+β+α=180°2α+β=180°通过重排项，我们可以得到：β=180°-2α所以，我们已经确定了角A、角B和角C的度数之间的关系。

综上所述，我们可以得出以下结论：在任意三角形中，三个内角的和是180°。

三角形的内角和外角三角形是几何学中最基本的形状之一，它由三条边组成。

在三角形内部，存在三个内角，而在三角形外部，也存在着三个外角。

本文将深入讨论三角形的内角和外角的性质和关系。

一、三角形内角的性质1. 内角定义：三角形内角是三角形的内部角度，具体可分为三个角度，分别记为∠A、∠B和∠C，对应于三角形的三个顶点A、B和C。

2. 内角和定理：在任意三角形ABC中，三个内角的和等于180度，即∠A + ∠B + ∠C = 180°。

3. 内角的大小：根据内角和定理可知，对于普通三角形，其中至少一个内角小于90度，至少一个内角大于90度。

4. 直角三角形内角：直角三角形是一种特殊的三角形，其中一个内角为90度，另外两个内角之和必然为90度。

5. 三角形内角的分类：根据大小可将三角形的内角分为锐角、直角和钝角。

当三角形中的一个内角为锐角时，其余两个内角分别为钝角；当三角形中的一个内角为直角时，其余两个内角都为锐角；当三角形中的一个内角为钝角时，其余两个内角都为锐角。

二、三角形外角的性质1. 外角定义：三角形外角是指三角形的一个内角的补角，即等于360度减去该内角的度数。

2. 外角和定理：在任意三角形ABC中，三个外角的和等于360度，即∠D + ∠E + ∠F = 360°。

3. 外角与内角的关系：三角形内角与其对应的外角之和为180度，即∠A + ∠D = 180°，∠B + ∠E = 180°，∠C + ∠F = 180°。

4. 外角的分类：根据大小可将三角形的外角分为锐角和钝角。

当三角形中的一个内角为锐角时，其对应的外角也为锐角；当三角形中的一个内角为钝角时，其对应的外角也为钝角。

三、三角形内角和外角的关系1. 内角和外角的关系：在任意三角形ABC中，三角形内角和其对应的外角之和等于180度，即∠A + ∠D = 180°，∠B + ∠E = 180°，∠C + ∠F = 180°。

三角形内角和的证明三角形是平面几何中的基本图形之一，它有三条边和三个角。

这篇文章将会证明一个结论：三角形的三个内角和为180度。

首先，我们来考虑一个边长为a，b，c的三角形ABC。

我们可以用三角形的三个顶点来定义三个向量a，b，c，这些向量的长度分别为a，b，c。

那么，我们可以在向量b上找到一个点D，使得AD与向量c重合，那么这条直线就称为CD。

（插入一张图，图中ABC为三角形）我们可以找到一个向量m，它垂直于向量b和CD。

那么向量m与向量b的夹角记为α，向量m和CD的夹角记为β，向量a和向量m的夹角记为γ。

现在，我们来看向量m与向量b的夹角α。

根据向量的点积公式，有：m·b = |m||b| cos(α) （1）因为向量m是垂直于向量b，所以m·b=0，所以：因为向量m和向量b的长度都是正数，所以cos(α)必须等于零，也就是说α=90度。

这意味着向量m是向量b的一个垂线。

同理，我们可以得到：因为α=90度，所以向量m和向量CD是平行的。

我们可以得到一个证明：同理：现在，我们来计算三角形ABC的面积S。

由于向量b和向量CD重合，所以S=1/2|b+c|·h，其中h为三角形ABC到CD的距离。

同理，又有S=1/2|a+c|·h这两式联立，得到：|b+c| = |a+c|这意味着三角形ABC的边长a，b，c之间满足某种关系：a²+b²=c²。

现在，我们可以用余弦定理来证明三角形的三个内角和为180度。

根据余弦定理：cosA = (b²+c²-a²)/2bccosB = (a²+c²-b²)/2accosC = (a²+b²-c²)/2ab现在，我们来计算cosA+cosB+cosC，有：= a²b² + b²c² + c²a² - a⁴ - b⁴ - c⁴ / 2abc= (a²+b²+c²) / 2abcosA + cosB + cosC = a / ccosA + cosB + cosC = b / a三个式子联立，解得cosA+cosB+cosC=1。

三角形内角6种证明方法
嘿，朋友们！今天咱就来聊聊三角形内角和那些事儿。

你说三角形
内角和为啥就是 180 度呢？嘿嘿，这可有 6 种证明方法哦，听我慢慢
道来。

第一种方法呢，就像是搭积木一样。

咱可以在三角形的一个顶点作
一条平行线，然后通过那些角度的关系，就像玩拼图一样，一下子就
看出来内角和是 180 度啦！你说神奇不神奇？
第二种方法呀，有点像走迷宫。

我们可以把三角形的三个角剪下来，然后拼在一起，哇塞，这不就拼成了一个平角嘛，平角就是180 度呀，这多直观！
第三种方法呢，像是变魔术。

我们利用外角和内角的关系，通过一
系列巧妙的转换，就能得出内角和啦。

第四种方法就好像解谜题。

通过一些几何定理和等式的推导，一步
一步地就能揭开内角和是 180 度的谜底。

第五种方法呢，如同寻找宝藏的线索。

从三角形的不同部分入手，
一点点地拼凑出内角和的真相。

第六种方法更是有趣，就像是走钢丝一样，需要精准地把握各种角
度的平衡。

你想想看，三角形多神奇啊，就那么三个角，却有着这么多种证明方法来确定它们的内角和。

这就好像我们生活中的很多事情，从不同的角度去看，就会有不一样的发现和理解。

这六种证明方法，就像是打开三角形内角和秘密的六把钥匙。

每一把都能让我们更深入地了解三角形的奥秘。

我们可以用它们来解决各种几何问题，就像战士拿着武器去战斗一样！难道这还不够酷吗？
所以啊，别小看这小小的三角形内角和，它里面蕴含的知识和乐趣可多着呢！朋友们，不妨自己也去试试这些证明方法，亲自感受一下几何的魅力吧！。

三角形的内角和数学整理笔记三角形是几何学中的重要概念，它具有许多独特的性质和规律。

其中，三角形的内角和是一个非常基础且重要的概念。

在本篇文章中，我们将对三角形的内角和进行详细的数学整理和笔记。

1. 三角形的定义和基本性质三角形是一个有三条边和三个角的多边形。

三角形的三个内角分别记为角A、角B和角C，对应的三条边分别记为a、b和c。

三角形的内角和是指三个内角的和，即角A + 角B + 角C = 180°。

2. 三角形的内角和定理三角形的内角和定理是三角形几何学中的一个重要定理，它指出任意一个三角形的三个内角的和总是等于180°。

这个定理对于任意三角形都成立，不论是等边三角形、等腰三角形还是普通三角形。

3. 三角形内角和的推导三角形的内角和的推导可以通过几何推理和角度关系进行证明。

以三角形ABC为例，我们可以通过以下步骤来推导三角形的内角和：- 通过角的外角和定理，角A的外角等于角B + 角C- 角A的外角等于角的和减去角的内角- 角的和等于180°，所以角A的外角等于180° - 角A- 角A的外角等于角B + 角C，所以180° - 角A = 角B + 角C- 将角A、角B和角C代入，得到角A + 角B + 角C = 180°4. 三角形内角和的应用三角形的内角和是许多三角形性质和角度计算的基础。

在解决三角形的角度问题时，我们可以通过三角形的内角和定理来计算角的大小和角的关系，从而推导出三角形的各种角度性质和角的关系。

三角形的内角和也是解决三角形的角度问题和角的关系的重要工具。

总结：三角形的内角和是三角形的基本性质和角的关系，它对于理解三角形的角度性质和角的关系具有重要的意义。

通过本文的数学整理和笔记，我们可以更好地理解三角形的内角和的概念和角的关系，为解决三角形角度的问题和角的关系提供基础和工具。

三角形的内角和的定理和角的角度的推导和应用，是三角形角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角的角。

三角形内角和与外角和的几种常见应用类型与解题技巧类型一、截角和折叠综合求角度1、如图，在△ABC中，∠C＝70°，若沿图中虚线截去∠C，则∠1＋∠2 等于( )A．360°B．250°C．180°D．140°2、如图，将△ABC沿着DE翻折，使B点与B′点重合，若∠1＋∠2＝80°，求∠B 的度数．类型二、两个内角平分线的夹角方法归纳：三角形的两个内角平分线交于一点，所形成的夹角的度数等于90°加上第三角度数的一半．1、如图，在△ABC中，∠ABC与∠ACB的角平分线相交于点O，则∠BOC＝90°1＋∠A（两种方法）.22、如图，点O是△ABC的∠ABC与∠ACB两个角的平分线的交点，若∠BOC ＝118°，则∠ A 的角度是________°. 21 教育网如图所示，在△ABC中，BO、CO是角平分线．(1) ∠ABC＝50°，∠ACB＝60°，求∠BOC的度数，并说明理由；(2) 题(1) 中，如将“∠ABC＝50°，∠ACB＝60°”改为“∠A＝70°”，求∠BOC的度数；(3) 若∠A＝n°，求∠BOC的度数．类型三、一个内角平分线与一个外角平分线的夹角方法归纳：三角形的一个内角平分线与一个外角平分线交于一点，所形成的夹角的度数等于第三角度数的一半．1、如图，在△ABC中，BD、CD分别平分∠ABC、∠ACE，则∠BDC ＝12∠A. （两种方法）2、如图，在△ABC中，∠ABC的平分线与∠ACB的外角平分线交于点D，∠A＝50°，则∠D＝________ ．3、如图，在平面直角坐标系中，A，B 分别是x，y 轴上的两个动点，∠BAO 的平分线与∠ABO的外角平分线相交于点C，在A，B 的运动过程中，∠ C 的度数是一个定值，这个定值为________ ．5．( 达州中考改编)如图，在△ABC中，∠A＝m°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC 和∠A1CD的平分线交于点A2，得∠A2；⋯∠A2 014 BC和∠A2 014 CD的平分线交于点A2 015 ，则∠A2 015 的度数为________．类型四、两个外角平分线的夹角方法归纳：三角形的两个外角平分线交于一点，所形成的夹角度数等于90°减去第三角度数的一半．1、如图，在△ABC中，BD、CD分别是△ABC外角∠EBC、∠FCB的平分线，求证∠BDC＝90°－1∠A. 22、如图，在△ABC中，P点是∠BCE和∠CBF的角平分线的交点，若∠A＝60°，则∠P＝________．类型五、角平分线与高线的夹角方法归纳：三角形同一顶点的高线与角平分线的夹角度数等于另外两角度数之差的一半．1、如图，在△ABC中，AD⊥BC于D，AE平分∠BAC，求证∠EAD ＝12( ∠B－∠C)．( 其中∠B＞∠C)2、如图，在△ABC中，∠B＝45°，∠EAD＝10°，AD⊥BC 于D，AE是∠BAC的平分线，则∠C的度数为________ ．3、如图，△ABC中，AE平分∠BAC，∠B＝40°，∠C＝70°，F 为射线AE上一点( 不与 E 点重合) ，且FD⊥BC.(1) 若点 F 与点 A 重合，如图1，求∠EFD的度数；(2) 若点 F 在线段AE上( 不与点 A 重合) ，如图2，求∠EFD的度数；(3) 若点 F 在△ABC外部，如图3，此时∠EFD的度数会变化吗？是多少？4、如图，在△ABC中，AD是高，AE是角平分线，∠B＝20°，∠C＝60°.(1) 求∠CAD、∠AEC和∠EAD的度数；(2) 若图形发生了变化，已知的两个角度数改为：当∠B＝30°，∠C＝60°时，则∠EAD＝________；当∠B＝50°，∠C＝60°时，则∠EAD＝________；当∠B＝60°，∠C＝60°时，则∠EAD＝________；当∠B＝70°，∠C＝60°时，则∠EAD＝________.(3) 若∠B 和∠C 的度数改为用字母α和β来表示，你能找到∠EAD与α和β之间的关系吗？请直接写出你发现的结论．21 世纪教育网版权技巧一、利用外角与内角的关系进行“聚角”( 集中)方法归纳：将位置分散的角集中在一个图形内，然后利用三角形( 或多边形) 的内角和求解．1、如图，求∠A＋∠B＋∠C＋∠D＋∠E.2、如图，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F.3、如图，求∠A＋∠ABC＋∠C＋∠D＋∠E＋∠F 的度数．技巧二、利用“8”字形转化角( 补形)方法归纳：求凹多边形的内角和时，可将其补成凸多边形，然后利用多边形的内角和计算公式求解．1、如图，求∠A＋∠B＋∠C＋∠D＋∠E.2、如图，∠A＋∠B＋∠C＋∠D＋∠1 的度数为________．3、如图所示，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F 的度数．4、如图，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F.5、如图，求∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7.。

三角形的内角和（基础）知识讲解【学习目标】1．理解三角形内角和定理的证明方法；2．掌握三角形内角和定理及三角形的外角性质；3．能够运用三角形内角和定理及三角形的外角性质进行相关的计算，证明问题.【要点梳理】要点一、三角形的内角和三角形内角和定理：三角形的内角和为180°．要点诠释：应用三角形内角和定理可以解决以下三类问题：①在三角形中已知任意两个角的度数可以求出第三个角的度数；②已知三角形三个内角的关系，可以求出其内角的度数；③求一个三角形中各角之间的关系．要点二、三角形的外角1．定义：三角形的一边与另一边的延长线组成的角叫做三角形的外角．如图，∠ACD是△ABC的一个外角.要点诠释：(1)外角的特征：①顶点在三角形的一个顶点上；②一条边是三角形的一边；③另一条边是三角形某条边的延长线．（2）三角形每个顶点处有两个外角，它们是对顶角．所以三角形共有六个外角，通常每个顶点处取一个外角，因此，我们常说三角形有三个外角．2．性质：（1）三角形的一个外角等于与它不相邻的两个内角的和．（2）三角形的一个外角大于任意一个与它不相邻的内角．要点诠释：三角形内角和定理和三角形外角的性质是求角度及与角有关的推理论证明经常使用的理论依据．另外，在证角的不等关系时也常想到外角的性质．3.三角形的外角和：三角形的外角和等于360°.要点诠释：因为三角形的每个外角与它相邻的内角是邻补角，由三角形的内角和是180°，可推出三角形的三个外角和是360°．【典型例题】类型一、三角形的内角和1．证明：三角形的内角和为180°.【答案与解析】解：已知：如图，已知△ABC，求证：∠A+∠B+∠C＝180°.证法1：如图1所示，延长BC 到E ，作CD ∥AB ．因为AB ∥CD （已作），所以∠1=∠A （两直线平行，内错角相等），∠B=∠2（两直线平行，同位角相等）．又∠ACB+∠1+∠2=180°（平角定义），所以∠ACB+∠A+∠B=180°（等量代换）．证法2：如图2所示，在BC 边上任取一点D ，作DE ∥AB ，交AC 于E ，DF ∥AC ，交AB 于点F ．因为DF ∥AC （已作），所以∠1=∠C （两直线平行，同位角相等），∠2=∠DEC （两直线平行，内错角相等）．因为DE ∥AB （已作）．所以∠3=∠B ，∠DEC=∠A （两直线平行，同位角相等）．所以∠A=∠2（等量代换）．又∠1+∠2+∠3=180°（平角定义），所以∠A+∠B+∠C=180°（等量代换）．证法3：如图3所示，过A 点任作直线1l ，过B 点作2l ∥1l ，过C 点作3l ∥1l ， 因为1l ∥3l （已作）．所以∠l=∠2（两直线平行，内错角相等）．同理∠3=∠4．又1l ∥2l （已作），所以∠5+∠1+∠6+∠4=180°（两直线平行，同旁内角互补）．所以∠5+∠2+∠6+∠3=180°（等量代换）．又∠2+∠3=∠ACB，所以∠BAC+∠ABC+∠ACB=180°（等量代换）．证法4：如图4，将ΔABC的三个内角剪下，拼成以C为顶点的平角.证法5：如图5－1和图5－2，在图5－1中作∠1＝∠A，得CD∥AB，有∠2＝∠B；在图5－2中过A作MN∥BC有∠1＝∠B，∠2＝∠C，进而将三个内角拼成平角.【总结升华】三角形内角和定理的证明方法有很多种，无论哪种证明方法，都是应用的平行线的性质.2.（2016春•宜兴市校级月考）如图，BE是∠ABD的平分线，CF是∠ACD的平分线，BE与CF交于G，若∠BDC=140°，∠BGC=110°，则∠A为（）A．70°B．75°C．80°D．85°【思路点拨】首先根据三角形的内角和定理，求出∠1+∠2=40°，∠1+∠2+∠3+∠4=70°；然后判断出∠3+∠4=30°，再根据BE是∠ABD的平分线，CF是∠ACD的平分线，判断出∠5+∠6=30°；最后根据三角形的内角和定理，用180°减去∠1+∠2+∠3+∠4+∠5+∠6的度数，求出∠A为多少度即可．【答案与解析】解：如图，∵∠BDC=140°，∴∠1+∠2=180°﹣140°=40°，∵∠BGC=110°，∴∠1+∠2+∠3+∠4=180°﹣110°=70°，∴∠3+∠4=70°﹣40°=30°，∵BE是∠ABD的平分线，CF是∠ACD的平分线，∴∠3=∠5，∠4=∠6，又∵∠3+∠4=30°，∴∠5+∠6=30°，∴∠1+∠2+∠3+∠4+∠5+∠6=（∠1+∠2+∠3+∠4）+（∠5+∠6）=70°+30°=100°∴∠A=180°﹣100°=80°．故选：C．【总结升华】此题主要考查了三角形的内角和定理，要熟练掌握，解答此题的关键是要明确：三角形的内角和是180°．举一反三：【变式】已知，如图，在△ABC中，∠C=∠ABC=2∠A，BD是AC边上的高，求∠DBC的度数.【答案】解：已知△ABC中，∠C=∠ABC=2∠A设∠A=x则∠C=∠ABC=2xx+2x+2x=180°解得：x=36°∴∠C=2x=72°在△BDC中， BD是AC边上的高，∴∠BDC=90°∴∠DBC=180°－90°-72°=18°类型二、三角形的外角3.（1）如图，AB和CD交于交于点O，求证：∠A＋∠C＝∠B＋∠D ．（2）如图，求证：∠D=∠A＋∠B +∠C．【答案与解析】解：（1）如图，在△AOC中，∠COB是一个外角，由外角的性质可得：∠COB＝∠A＋∠C，同理，在△BOD中，∠COB＝∠B＋∠D，所以∠A＋∠C＝∠B＋∠D．（2）如图，延长线段BD交线段与点E，在△ABE中，∠BEC＝∠A＋∠B ①；在△DCE中，∠BDC＝∠BEC＋∠C ②，将①代入②得，∠BDC＝∠A＋∠B＋∠C，即得证．【总结升华】重要结论：（1）“8”字形图：∠A＋∠C＝∠B＋∠D；（2）“燕尾形图”：∠D=∠A＋∠B +∠C．举一反三：【变式1】（新疆建设兵团）如图，AB∥CD，AD和BC相交于点O，∠A＝40°，∠AOB＝75°，则∠C等于（）A、40°B、65°C、75°D、115°【答案】B【变式2】（2015春•龙口市）如图，∠A+∠B+∠C+∠D+∠E的度数为度．【答案】如图连接CE，根据三角形的外角性质得∠1=∠A+∠B=∠2+∠3，在△DCE中有，∠D+∠2+∠DCB+∠3+∠AED=180°，∴∠D+∠A+∠DCB+∠B+∠AED=180°．类型三、三角形的内角外角综合4.（2015春•绿园）如图，∠ABC=38°，∠ACB=100°，AD平分∠BAC，AE是BC边上的高，求∠DAE的度数．【思路点拨】先根据三角形内角和定理求出∠BAC的度数，由角平分线的定义得出∠BAD的度数，根据三角形外角的性质求出∠ADE的度数，由两角互补的性质即可得出结论．【答案与解析】解：∵∠ABC=38°，∠ACB=100°（己知）∴∠BAC=180°﹣38°﹣100°=42°（三角形内角和180°）．又∵AD平分∠BAC（己知），∴∠BAD=21°，∴∠ADE=∠ABC+∠BAD=59°（三角形的外角性质）．又∵AE是BC边上的高，即∠E=90°，∴∠DAE=90°﹣59°=31°．【总结升华】此题考查的是三角形的内角和定理，熟知三角形内角和是180°是解答此题的关键．举一反三：【变式】如图所示，已知△ABC 中，P 为内角平分线AD 、BE 、CF 的交点，过点P 作PG ⊥BC 于G ，试说明∠BPD 与∠CPG 的大小关系并说明理由．【答案】解：∠BPD ＝∠CPG ．理由如下：∵ AD 、BE 、CF 分别是∠BAC 、∠ABC 、∠ACB 的角平分线，∴ ∠1＝12∠ABC ，∠2＝12∠BAC ，∠3＝12∠ACB ． ∴ ∠1+∠2+∠3＝12(∠ABC+∠BAC+∠ACB )＝90°． 又∵ ∠4＝∠1+∠2，∴ ∠4+∠3＝90°．又∵ PG ⊥BC ，∴ ∠3+∠5＝90°．∴ ∠4＝∠5，即∠BPD ＝∠CPG ．。

三角形内角和定理推论教学目标1、掌握“三角形内角和定理”的证明及其应用；2、掌握在证明三角形内角和定理时所引辅助线的作用；3、理解、掌握三角形外角的概念、性质及其应用。

教学内容一、重难点讲解知识点一、三角形内角和定理（1）三角形内角和定理：三角形的内角和等于180°（2）辅助线：在证明过程中，为了证明的需要，在原来的图形上添画的线叫做辅助线（3）三角形内角和的证明：①证法一：如右图，作BC的延长线CD，过点C作CE∥BA，则∠1=∠A（两直线平行，内错角相等），∠2=∠B（两直线平行，同位角相等）又∵∠1+∠2+∠ACB＝180°∴∠A+∠B+∠ACB＝180°②证法二：如右图，过点C作DE∥AB，则∠1＝∠B，∠2＝∠A又∵∠1+∠ACB+∠2＝180°∴∠A+∠ACB+∠B＝180°③证法三：如右图，在BC上任取一点D，作DE∥BA交AC于E，DF∥CA交AB于F则有∠2＝∠B，∠3＝∠C，∠1＝∠4，∠4＝∠A∴∠1＝∠A 又∵∠1+∠2+∠3＝180°∴∠A+∠B+∠C＝180°理解：（1）证明三角形内角和定理的方法有很多，基本思路是：把三角形的三个角“搬”到一起，让三个角的顶点重合、两边形成一条直线，以便利用平角的定义证明。

（2） ①一个三角形中最多只有一个钝角或直角②一个三角形中最少有一个角不小于60° ③等边三角形每个角都是60°知识点二、三角形外角三角形外角：由三角形的一边与另一边的延长线组成的角，叫做三角形的外角。

理解：（1）判定一个角是三角形外角的三个条件：一是顶点在三角形的一个顶点上，二是一边是三角形的一边，三是一边是三角形另一边的延长线；（2）三角形的每个顶点处，一个外角和它相邻的内角组成一个平角。

知识点三、三角形内角和定理的推论 推论1：直角三角形的两锐角互余推论2：有两个角互余的三角形是直角三角形 推论3：三角形的外角等于它不相邻的两个内角和 推论4：三角形的外角大于与它不相邻的任何一个内角二典型例题例1：△ABC 中，∠B ，∠C 的平分线交于点O ，若∠BOC=132°，则∠A =________.例2：如图1，AB//CD ，AE 交CD 于C ，︒=∠︒=∠9056DEC A ，，则D ∠的度数为（ B ） （A ）17° （B ）34° （C ）56° （D ）124°图1 图2例3：设α，β，γ是某三角形的三个内角,则α+β，β+γ，α+γ 中 ( ) （A ）有两个锐角一个钝角 （B ）有两个钝角、一个锐角 （C ）至少有两个钝角 （D ）三个都可能是锐角例4:（1）如图2①，五角形的顶点分别为A 、B 、C 、D 、E ，∠A+∠B+∠C+∠D+∠E=________（2）如图2②，∠A+∠DBE+∠C+∠D+∠E=________（3）（3）如图2③，∠A+∠B+∠C+∠D+∠E=________例5：如图3，AD为△ABC的中线，BE为三角形ABD中线，（1）∠ABE=15°，∠BAD=35°，求∠BED的度数；（2）在△BED中作BD边上的高；（3）若△ABC的面积为60，BD=5，则点E到BC边的距离为多少？图3例6：如图4，DB是△ABC的高，AE是角平分线，∠BAE=26°，求∠BFE的度数．图4例7：如图5，在△ABC中，AD平分∠BAC，P为线段AD上的一个动点，PE⊥AD交直线BC于点E．（1）若∠B=35°，∠ACB=85°，求∠E的度数；（2）当P点在线段AD上运动时，猜想∠E与∠B、∠ACB的数量关系，写出结论无需证明．图5三、过关检测1、如果三角形的三个内角的度数比是2：3：4，则它是( )（A ）锐角三角形 （B ）钝角三角形 （C ）直角三角形 （D ）钝角或直角三角形 2、下列说法正确的是( )（A ）三角形的内角中最多有一个锐角 （B ）三角形的内角中最多有两个锐角 （C ）三角形的内角中最多有一个直角 （D ）三角形的内角都大于60° 3、如图1，∠1、∠2、∠3的大小关系为（ ） （A ）∠2＞∠1＞∠3 （B ）∠1＞∠3＞∠2 （C ）∠3＞∠2＞∠1 （D ）∠1＞∠2＞∠3图14、如果三角形的一个外角和与它不相邻的两个内角的和为180°,那么与这个外角相邻的内角的度数为( )（A ）30° （B ）60° （C ）90° （D ）1205、一个零件的形状如图2，按规定∠A= 90°，∠B 和∠C 应分别是32°和21°，检验工人量得∠BDC = 148°，就断定这个零件不合格，运用三角形的有关知识说明零件不合格的理由。