结构力学专题十五(结构的极限荷载)
- 格式:ppt
- 大小:556.00 KB
- 文档页数:16








Harbin Institute of Technology超静定梁中的极限荷载的研究课程名称:结构力学院系:土木工程学院班级:1433111姓名:李渊学号: 1143310120摘要:大多数工程材料,特别是钢材,受力后发生变形,一般都存在线性弹性阶段、屈服阶段和强化阶段。
因此,随着荷载的增加,结构截面上应力大的点首先达到屈服强度,发生屈服,结构将进入弹塑性状态。
这时虽然截面部分材料已进入塑性状态,但尚有相当大的部分材料仍处于弹性范围,因而结构仍可继续加载。
当荷载增加到一定程度,结构中进入塑形的部分不断扩展直至完全丧失承载能力,导致结构崩溃(或倒塌)。
因此研究结构极限状态下的极限荷载,是十分有必要的,对于结构安全储备的考虑的依据提供有重要意义。
正文:一、极限荷载的有关意义定义:结构出现塑性变形直到崩溃时所能承受的最大荷载,称为极限荷载,它是考虑结构安全储备设计依据的因素之一,且按极限状态设计结构比弹性设计更经济。
通过对弹性设计方法及其许用应力设计法的研究,并在其方面进行了探讨,得到弹性设计方法及其许用应力设计法的最大缺陷是以某一截面上的max σ达到[σ]作为衡量整个结构破坏的标准。
事实上,由塑性材料组成的结构(特别是超静定结构)当某一局部的max σ达到了屈服应力时,结构还没有破坏,还能承受更大的荷载。
因此弹性设计法不能充分的利用结构的承载能力,是不够经济的。
塑性分析考虑了材料的塑性性质,其强度要求以结构破坏时的荷载作为标准:max []PuP p uF F F k ≤=其中,Pu F 是结构破坏时荷载的极限值,即极限荷载。
u k 是相应的安全系数。
对结构进行塑性分析时仍然要用到平衡条件、几何条件、平截面假定,这与弹性分析时相同。
另外还要采用以下假设:图1(1)材料为理想弹塑性材料。
其应力与应变关系如图所示。
(图1)(2)比例加载:全部荷载可以用一个荷载参数P 表示,不会出现卸载现象。
(3)结构的弹性变形和塑性变形都很小。

第11章 结构的极限荷载前面各章所讨论的结构计算均是以线弹性结构为基础的,即限定结构在弹性范围内工作。
当结构的最大应力达到材料的极限应力n σ时,结构将会破坏,故强度条件为[]max nKσσσ=≤ 式中,max σ为结构的最大工作应力;[]σ为材料的许用应力;n σ为材料的极限应力,对于脆性材料为其强度极限b σ,对于塑性材料为其屈服极限s σ;K 为安全系数。
基于这种假定的结构分析称为弹性分析。
从结构强度角度来看,弹性分析具有一定的缺点。
对于塑性材料的结构,尤其是超静定结构,在某一截面的最大应力达到屈服应力,某一局部已进入塑性阶段时,结构并不破坏,还能承受更大的荷载继续工作,因此按弹性分析设计是不够经济合理的。
另外,弹性分析无法考虑材料超过屈服极限以后,结构的这一部分的承载能力。
塑性分析方法就是为了弥补弹性分析的不足而提出和发展起来的。
它充分地考虑了材料的塑性性质,以结构完全丧失承载能力时的极限状态作为结构破坏的标志。
此时的荷载是结构所能承受荷载的极限,称为极限荷载,记为u F 。
结构的强度条件可表示为u F F K≤ 式中F 为结构工作荷载,K 为安全系数。
显然,塑性分析的强度条件比弹性分析更切合实际。
塑性分析方法只适用于延展性较好的塑性材料的结构,对于脆性材料的结构或对变形有较大限制的结构应慎用这种方法。
对结构进行塑性分析时,平衡条件和几何条件与弹性分析时相同,如平截面假设仍然成立,所不同的是物理条件。
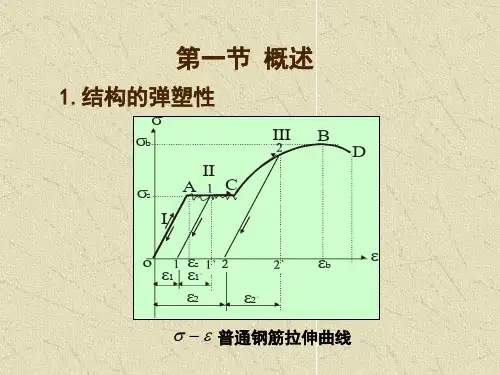
为了简化计算,对于所用的材料,常用如图11.1所示的应力—应变曲线。
当应力达到屈服极限以前,材料处于弹性阶段,应力与应变成正比;当应力达到屈服极限s σ时,材料开始进入塑性变形阶段,应力保持不变,应变可无限增加;卸载时,材料恢复弹性但存在残余变形。
凡符合这种应力—应变关系的材料,称为理想弹塑性材料。
实际钢结构一般可视为理想弹塑性材料。
对于钢筋混凝土受弯构件,在混凝土受拉区出现裂缝后,拉力完全由钢筋承受,故也可采用这种简化的应力—应变曲线进行塑性分析。
qql 2/8 b σ ε 应 力 应 变塑性区 σy 第十五章 梁和刚架的极限荷载15.1 概述一、弹性分析材料在比例极限内的结构分析。
它是以许用应力为依据确定截面或进行验算的。
(低碳钢拉伸图)1、设计:[]σmaxM w ≥2、验算:[]σσ≤==I yM W M max max二、塑性分析按照极限状态进行结构设计的方法。
结构破坏瞬时对应的荷载称为“极限荷载”;,相应的状态称为“极限状态”。
三、基本假设 1、材料为“理想弹塑性材料” 。
2、拉压时,应力、应变关系相同。
3、满足平截面假定。
即无论弹、塑性阶段,保持平截面不变。
15.2 极限弯矩 塑性铰及破坏机构 一、屈服弯矩与极限弯矩1、屈服弯矩(My): 截面最外侧纤维的应力达到流动极限时对应的弯矩。
2、极限弯矩(Mu):弯矩。
3、截面形状系数:极限弯矩与屈服弯矩之比yhh y h h y h h bh y h b bydy h y y bdy σσσσ632 2M 22232222y =⋅=⋅=⋅⋅=---⎰⎰矩形截面:y d σπ32 M 3y =圆形截面:y22h2h 2y 2h 2h y u σ4bh 2y b σy bdy σM 矩形截面:=⋅=⋅=--⎰y 3u σ6dM 圆形截面:=y y s σs σσdy yu Yu W W M M α==⎪⎪⎩⎪⎪⎨⎧===1.15 316 1.5 απαα工字形截面:圆形截面:矩形截面:σyy A σ1yA σ2•⨯h b yA σ1y A σ2•⨯122ql 122ql 242(1)弹性阶段q 122l q s 12l q s242ls (2)弹性阶段末2u q u 1u q uM u M 8222l q M u u +M u u u u M l q =1221u u M l q =122122421u u M l q =(3)梁两端出现塑性铰 q令22164l M l M uu =+(4)极限状态 确定单跨梁极限荷载的机动法 q θθθθ2 221⋅+⋅+⋅=⋅⎰u u u l u M M M dx q x 2216 441 l M q M q l u u u u =∴=⋅θθA 确定单跨梁极限荷载的静力法quM uM u M uM 2lq u q B极限状态受力图0lq V y u ==4、截面达到极限弯矩时的特点 极限状态时,无论截面形状如何,中性轴两侧的拉压面积相等。