有理数的乘法(2)
- 格式:ppt
- 大小:2.41 MB
- 文档页数:12

七年级第二章第七节有理数的乘法(2)课型:新授课教学目标:1.认识有理数乘法中运算律的作用;2.理解有理数的乘法中,运用运算律的方法;3.掌握用乘法法则进行有理数乘法运算,用运算律简化计算的方法.教法与学法指导:本课是有理数乘法的进一步拓展.因为学生已经学习了有理数的乘法,因此在知识内容和教学方法上,采用“自主学习—合作探究—当堂达标”的模式进行教学,引导学生探究有理数的乘法运算律,并能正确运用乘法运算律简化计算.重点:用运算律简化有理数乘法运算.难点:会运用乘法运算律进行有理数乘法的简便运算.课前准备:教师:多媒体课件,提前发放导学案.教学过程:一、创设情境,导入新课师:请同学们计算一4×8×125×25等于多少? (多媒体展示)(找两位学生黑板上板书)学生甲:4×8×125×25 学生乙:4×8×125×25=32×125×25 =(4×25)×(8×125)=4000×25 =100×1000=100000 =100000师:这两位同学做的都对吗?生:对.师:哪一种做法更简单?生:乙.师:你们能说出乙同学解题的依据吗?生:运用了乘法的交换律和结合律.师:好!乘法还有什么运算律?生:还有乘法分配律.师:在小学所学的运算中,乘法具有交换律、结合律和分配律,而现在同学们已经学习了有理数的乘法运算,在有理数的运算中,乘法的交换律、结合律和分配律还成立吗?这就是我们这节课探究的问题:(教师黑板板书) 有理数的乘法(2)设计意图:通过小学学习过的乘法运算律的复习,一方面让学生体会乘法运算律的简便性,另一方面为引入有理数乘法运算律做了铺垫,激发学生学习本节课的兴趣.二、目标展示师:看一下我们这节课的学习目标(多媒体展示)1.知道有理数乘法运算律;2.会用有理数乘法运算律简化乘法运算.三、自主学习,合作探究探究活动一:有理数乘法运算律师:为了解决这个问题,我们先来做一做以下题目.(多媒体展示,学生在导学案上解答)计算:(1)(-7)×8与8×(-7);(-35)×(-109)与(-35)×(-109). (2)[(-4) ×(-6)] ×5与(-4) ×[(-6) ×5]; [21×(-37)] ×(-4)与21×[(-37) ×(-4)]. (3)(-2)×[(-3)+(-23)]与(-2)×(-3)+(-2)×(-23) ; 5×[(-7)+(-54)]与5×(-7)+5 ×(-54). 学生做完后,教师选其中一个学生的进行投影,让其他学生进行点评、纠错。
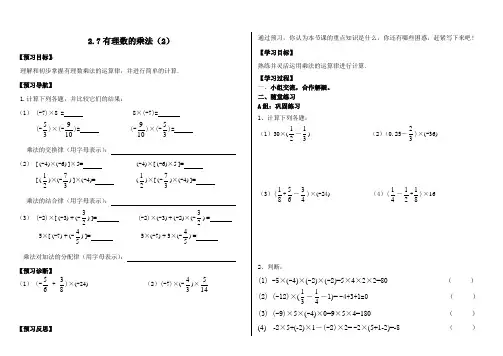
2.7有理数的乘法(2)【预习目标】:理解和初步掌握有理数乘法的运算律,并进行简单的计算. 【预习导航】1.计算下列各题,并比较它们的结果:(1) (-7)×8 = 8×(-7)= (-35)×(-109)= (-109)×(-35)=乘法的交换律(用字母表示): (2) [ (-4)×(-6) ]×5= (-4)×[ (-6)×5 ]= [ (21)×(-37) ]×(-4)= (21)×[ (-37)×(-4) ]= 乘法的结合律(用字母表示):(3) (-2)×[ (-3) + (-23) ]= (-2)×(-3) + (-2)×(-23) = 5×[ (-7) + (-54) ]= 5×(-7) + 5×(-54) =乘法对加法的分配律(用字母表示): 【预习诊断】 (1)(-65 + 83)×(-24) (2)(-7)×(-34)×145【预习反思】通过预习,你认为本节课的重点知识是什么,你还有哪些困惑,赶紧写下来吧! 【学习目标】熟练并灵活运用乘法的运算律进行计算. 【学习过程】一、小组交流,合作解疑。
二、随堂练习 A 组:巩固练习 1、计算下列各题: (1)30×(21-31) (2)(0.25-32)×(-36) (3)(81+65-43)×(-24) (4)(41-21+81)×162、判断:(1) -5×(-4)×(-2)×(-2)=5×4×2×2=80 ( )(2) (-12)×(31-41-1)= -4+3+1=0 ( )(3) (-9)×5×(-4)×0=9×5×4=180 ( ) (4) -2×5+(-2)×1-(-2)×2= -2×(5+1-2)=-8 ( ) B 组:能力提升 1.计算(1)(-2)×(-8)×(-125) (2) 8×(-54)×161(3) (-32)×72×(-43) (4) 0.25×(-3.1)×(-8) 2.计算(1) 53×17 + 53×8 (2)37×7+37×(-3)+37×6(3) 60×73-60×71+60×75 (4) 74×(-245)-(-73)×(-245)C 组:拓展延伸1. 有6张不同数字的卡片:—3,+2,0, —8, 5, +1,如果从中任取3张,(1)使数字的积最小,应如何抽?最小积是多少? (2)使数字的积最大,应如何抽?最大积是多少?2.已知:a 、b 互为相反数,c 、d 互为倒数,x 的绝对值是1,求:3x - [(a +b)+cd]x 的值3.定义一种运算符号△的意义:a △b=ab —1,。




教学内容:§1.5 有理数的乘法(1)教学目标:1、知识与技能使学生理解有理数乘法的意义,掌握有理数的乘法法则,能熟练地进行有理数的乘法运算。
2、过程与方法经历探索有理数乘法法则的过程,理解有理数乘法法则,发展观察、探究、合情推理等能力,会进行有理数和乘法运算。
重点、难点: 1、重点:有理数乘法法则。
2、难点:有理数乘法意义的理解,确定有理数乘法积的符号。
教学过程:一、创设情景,导入新课1、由前面的学习我们知道,正数的加减法可以扩充到有理数的加减法,那么乘法是可也可以扩充呢?乘法是加法的特殊运算,例如5+5+5=5×3,那么请思考:(-5)+(-5)+(-5)与(-5)×3是否有相同的结果呢?本节课我们就来探究这个问题。
3、在一条由西向东的笔直的马路上,取一点O,以向东的路程为正,则向西的路程为负,如果小玫从点O出发,以每小时5千米的向西行走,那么经过3小时,她走了多远?二、合作交流,解读探究1、小学学过的乘法的意义是什么?乘法的分配律:a×(b+c)=a×b+a×c如果两个数的和为0,那么这两个数 互为相反数 。
2、由前面的问题3,根据小学学过的乘法意义,小玫向西一共走了 (5×3)千米,即(-5)×3=-(5×3)3、学生活动:计算3×(-5)+3×5,注意运用简便运算通过计算表明3×(-5)与3×5互为相反数,从而有3×(-5)=-(3×5),由此看出,3×(-5)得负数,并且把绝对值3与5相乘。
类似的,(-5)×(-3)+(-5)×3=(-5)×[(-3)+3]=0 由此看出(-5)×(-3)得正数,并且把绝对值5与3相乘。
4、提出:从以上的运算中,你能总结出有理数的乘法法则吗?鼓励学生自己归纳,并与同伴交流。




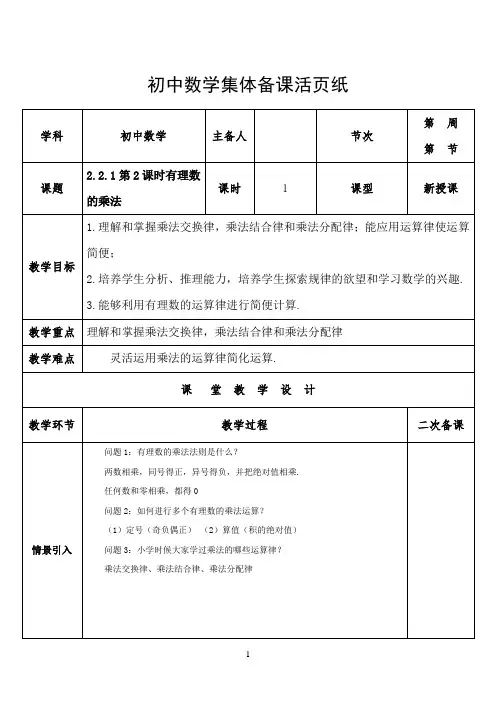
初中数学集体备课活页纸学科初中数学主备人节次第周第节课题2.2.1第2课时有理数的乘法课时 1 课型新授课教学目标1.理解和掌握乘法交换律,乘法结合律和乘法分配律;能应用运算律使运算简便;2.培养学生分析、推理能力,培养学生探索规律的欲望和学习数学的兴趣.3.能够利用有理数的运算律进行简便计算.教学重点理解和掌握乘法交换律,乘法结合律和乘法分配律教学难点灵活运用乘法的运算律简化运算.课堂教学设计教学环节教学过程二次备课情景引入问题1:有理数的乘法法则是什么?两数相乘,同号得正,异号得负,并把绝对值相乘. 任何数和零相乘,都得0问题2:如何进行多个有理数的乘法运算?(1)定号(奇负偶正)(2)算值(积的绝对值)问题3:小学时候大家学过乘法的哪些运算律?乘法交换律、乘法结合律、乘法分配律新知探究探究1 计算下列各题:5×(-6)= (-4)×(-8)= (-9)×4=(-6)×5= (-8)×(-4)= 4×(-9)=从上述计算中,你能得出什么结论?探究2 计算下列各题:[3×(-4)]×(-5)= [2×(-3)]×(-6)= 3×[(-4)×(-5)]= 2×[(-3)×(-6)]= 从上述计算中,你能得出什么结论?探究3 计算下列各题:5×[3+(-7)]= 10×[4+(-3)]=5×3+5×(-7)= 10×4+10×(-3)= 从上述计算中,你能得出什么结论?巩固练习例3 (1)计算2×3×0.5×(-7); (2)用两种方法计算(216141-+)×12.1.计算:(1) (6541121-+-) ×36.(2)161519×(-8).探究4 改变例3(1)的乘积式子中某些乘数的符号,得到下列一些式子观察这些式子,它们的积是正的还是负的?2×3×(-0.5)×(-7),2×(-3)×(-0.5)×(-7),(-2)×(-3)×(-0.5)×(-7).思考:几个不为0的数相乘,积的符号与负的乘数的个数之间有什么关系? 如果有乘数为0,那么积有什么特点?2.[2024·绍兴越城区月考]4个非零有理数相乘,积的符号是负号,则这4个有理数中,正数有( )A.1个B.2个C.3个D.1个或3个拓展提高1.计算:(1)(125-)×158×21×(32-);(2)(-1)×(45-)×158×23×(32-)×0×(-1)2. [2024上海宝山区期末]若-3,5,a的积是一个负数,则a的值可以是( )A.-15B.-2C.0D.153. 【新考向·知识情境化】小阳在计算65-×71×■时,不小心将一滴墨水滴在了本子上,盖住了其中一个数字,导致他无法计算,在求助老师时,老师告诉他:“被盖住的数字是4,7,10,11中的一个,并且这道题直接用乘法结合律来计算会非常简便”,则被盖住的数字最可能是( )A.4B.7C.10D.11课堂小结有理数乘法运算律1.乘法交换律:两个数相乘,交换两个因数的位置,积不变.ab=ba2.乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变.(ab)c=a(bc)3.乘法分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加.a(b+c)=a(b+c)板书设计2.2.1第2课时有理数的乘法1.ab=ba2. (ab)c=a(bc)3.a(b+c)=a(b+c)教学后记。
1.4.1有理数的乘法(2):1.有理数的乘法法则:两数相乘,同号得正,异号得负,并把所得的绝对值相乘。
任何数与0相乘,都得0.2.乘积是1的两个数互为倒数。
3.几个不是0的数相乘,负因数的个数是偶数时,积是正数,负因数的个数是奇数时,积是负数。
4.几个数相乘,如果其中有因数为0,那么积等于0.5、有理数乘法的法则:(1)两个数相乘,交换因数的位置,积相等。
a×b=b×a(2)三个数相乘,先把前两个相乘,或者先把后两个数相乘,积相等。
(ab)c=a(bc)(3)一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加。
a(b+c)=ab+ac自主学习一:阅读p32页,例如:5×(—6)= ,(—6)×5=则:5×(—6)(—6)×5乘法的交换律:ab=例如:计算[3×(—4)]×(—5)3×[(—4)×(—5)]比较它们的结果。
乘法结合律:(ab)c=例如:5×[3+(—7)] 5×3+5×(—7)乘法的分配律:a(b+c)=例4:用两种方法计算111+462⨯(—)12练一练:1.(—85)×(—25)×(—4)2.9130 1015⎛⎫⨯ ⎪⎝⎭—3.711587⎛⎫⨯⨯⎪⎝⎭—(—1)4.62617++5353⎛⎫⨯⨯⎪⎝⎭—(—)(—)()5.81.25825⎛⎫⨯⨯⎪⎝⎭—(—)自主探究:314⨯(—35)(—7)1832⨯—25157116⨯(—8)综合应用:111721+7732222⨯⨯⨯(3)(31121111+43232322⨯⨯⨯⨯(—2)(—4)—(—2)(4)—21.下列说法正确的有( )①.两数相乘,若积为正数,则这两个因数都是整数②同号两数相乘,取原来的符号,并把绝对值相乘③两数相乘,若积为负数,则这两个因数都是负数④.一个数乘以—1,便得这个数的相反数A.1个B.2个C.3个D.4个2.下列计算正确的是( )A.—5×(—4)×(—2)×(—2)=5×4×2×2=80B.11=++=34⨯(—12)(——1)—4310C.(—9)×(—4)×5×0=9×4×5=180D.—2×5—2×(—1)—(—2)×2=—2×(5+1—2)=—83.|—3|的倒数是( )A. —3B. 3C. 13—D. 134.如果两个数的乘积是正数,那么这两个有理数一定是( )A.都是正数B. 都是负数C. 符号相同D. 符号相反5.在—2,3,4,—5这四个数中,任取两个数相乘,所得的积是最大的是()A.20B. —20C. 12D.—126.已知|a|=1,|b|=2,则a 与b 的乘积等于( )A. 2B. —2C. ±2D. 07.计算41+=+54⨯—(10 ,这一步应用的运算律是( )A.加法结合律B. 乘法结合律C. 乘法交换律D.乘法分配律8.绝对值不大于4的所有的负整数的积等于( )A.—24B. 24C. 0D. —6 9.已知a <0,—1<b <0,则a ,ab ,ab 2,由大到小的顺序排列10.如果有理数a 的倒数的相反数是23—,那么这个数a 是11.已知|m|=8,|n|=6,m+n <0,则 1mn=212.计算:+⨯⨯(—6)(25)(—0.04) (97 -65 +43 -187 )×36(-5)×(+731 )+(+7)×(-731)-(+12)×73113.运用运算规律计算:1.25⨯⨯⨯⨯⨯(—2.5)(—0.5)428 249925⨯(—5)14.设A B A B A B *=⨯++,例如,2*3=2×3+2+3=11,试计算下列各式,(1)1135*(—)(—)(2)[(—2)*4]*(—6)。
年级初一学科数学内容标题有理数的乘法2编稿老师白山【本讲教育信息】一、教学内容1.乘方的意义,运算及其符号法则;2.与乘方运算有关的规律探索问题二、知识要点1.乘方的概念:求n个相同因数a的积的运算叫做乘方.乘方的结果叫做幂,n叫做指数,a叫做底数.写出乘方运算(-3)4 底数是-3 ,指数是4,幂是81 .比较一下:求n个相同因数积的运算叫做乘方,求几个相同加数和的运算是乘法.2.乘方的符号法则:(1)正数的任何次幂都是正数;(2)负数的偶数次幂是正数,负数的奇数次幂是负数;(3)任何数的偶数次幂是非负数.即a2≥0(4)0的任何正整数次幂都是0.3.混合运算步骤先乘方,后乘除,再加减.三、重难点,考点分析有理数的乘方运算法则是重点,运算技能是难点;乘方运算及其符号法则是中考的常考内容.试题背景大都与生活实际相联系,一般以填空题,选择题的形式出现,是历年来中考的热点,属于低档题.【典例精析】( 的结果是()例1.计算3)1A.-1B. 1C.-3D. 3答案:A指导:本题考查了有理数的乘方运算,-1的奇数次幂是-1.例2.计算:(1)(-312)2(2)-0.62 (3)-(-3)4解:(1)(-312)2=(-72)2=(72)2=494(2)-0.62 =-0.36(3)-(-3)4=-34=-81指导:根据有理数的乘方法则及运算步骤,首先确定乘方的结果的符号,再计算绝对值的乘方.带分数乘方时,要把带分数化成假分数后再乘方;本例中注意区分(-3)4与-34的不同,防止因为符号而出现失误.例3.已知(a-1)2 +(b+3)2=0,求(a+b)3的值.解:因为(a-1)2 ≥0 (b+3)2 ≥0,且(a-1)2 +(b+3)2=0,所以(a-1)2=0 (b+3)2=0,所以a-1=0,b+3=0,所以a=1,b=-3 所以(a+b)3=(-3+1)3=-8指导:任何数的平方都是非负数,即a2≥0;非负数的性质:若几个非负数的和为零,则每个非负数均为零.例4.(1)计算:0.022,0.22 22202(2)从计算的结果看,你认为底数的小数点向右或者向左移动一位,移动两位……,平方数的小数点怎样移动?(3)底数的小数点向右或者向左移动一位,移动两位……,立方数的小数点怎样移动?举例验证.解:(1)0.022=0.0004 0.22 =0.04 22=4 202=400(2)底数的小数点向右或者向左移动一位,移动两位……,平方数的小数点向右或向左移动两位,移动四位……(3)底数的小数点向右或者向左移动一位,移动两位……,立方数的小数点向右或向左移动三位,移动六位……例如:0.013=0.000001 0.13=0.001 13=1 103=1000指导:本题给同学们提供了一个展示探索问题的平台,数学的许多重大发现都经历了观察,归纳,猜想,验证这样的思维过程.本题应先计算特例,再观察、总结规律,继而猜想与平方类似的立方的规律,然后举例验证.例5.(1)通过计算,探索规律:152=225可写成100×1×(1+1)+25252=625可写成100×2×(2+1)+25352=1225可写成100×3×(3+1)+25452=2025可写成100×4×(4+1)+25……752=5625可写成_______________________852=7225可写成________________________……(2)从第一题的结果,归纳猜想,得: (10n +5)2=___________________________ (3)根据上面的归纳猜想,请写出: 20052=_________________________________ 解:(1)752=5625可写成100×7×(7+1)+25852=7225可写成100×8×(8+1)+25 (2)(10n +5)2=100×n ×(n +1)+25 2指导:本例是一道由特殊事例总结出一般规律的考题,体现了“特殊——猜想——归纳——应用”的过程.观察(1)中前面几个等式可知:100,+1,+25是常量,而变量与等式左边平方数中5前面数字变化规律相同.【思想方法小结】乘方运算也应注意过程中包含的转化思想,乘方运算规律的探寻,则应注意培养观察、概括、推理能力的培养.【模拟试题】(时间60分钟,满分100分)一、填空题(每题4分,共20分)1. 乘方是 的特例,故乘方运算转化成_____________;2. 进行乘方运算时,先确定底数、指数;再确定幂的 ;用乘法求出 的绝对值.3. 在式子(-5)3中,底数是 ,指数是 ,幂是 ;4. 在式子-53中,底数是 ,指数是 ,幂是 .5. 的平方是449.二、选择题(每题4分,共12分)6. 一个数的平方为25,那么这个数是( ) A . -5 B . 5 C . ±25 D . ±57. 一个数的13次幂是-1,那么它的2009次幂是( ) A . -1B . 1C . ± 1D . 20098. 若(a -2)2+︱b +3︱=0,则(a +b )2008=( )A . 0B . 1C . -1D . 2008三、解答题(共68分)9. (24分)计算:(1)4)2(--;(2)3)21(--(3)2006)1(-;(4)20061-(5)3)32(-;(6)4)32(-(7)31--3×3)1(-;(8)23-÷2)3(-10. (6分)回答下列问题:计算比较:23-与2)3(-的值,你发现 . 11. (10分)(1)看一看下面两组算式(3×5)2 与32×52,〔(-13×4)〕2与(-13)2×42 每组两个算式的计算结果是否相等?(2)想一想,(ab )3 等于什么?(3)猜一猜,当n 为正整数时,(ab )n 等于什么?并试着说明你的结论的正确性. ﹡﹡12. (4分)观察下列等式: 1=113+23=32 13+23+33=62 13+23+33+43=102把这种规律用n 的等式表示出来_________________________________﹡13. (10分)计算:22.1 212.0 212,并比较结果,你有什么发现? 你的发现是:当两个2次幂的底数只有小数点不同时,幂也只有 不同,底数的小数点每向左(或向右)移动1位,幂的小数点就要相应的向 (或 )移动 .根据你的发现快速完成2120= ,21200= ,20012.0 . ﹡﹡14. (6分)小红拍球时,球落地后第一次跳起原来的21,又落地,然后又跳起上一次距地面距离的21…这样下去,第五次跳起的高度是多少米?(要列出式子) ﹡15. (8分)当x 取什么值时,式子4 2)1(--x 的值最大?最大值是多少?【试题答案】一、填空题1. 乘法 乘法2. 符号 积3. -5 3 -1254. 5 3 1255. ±27二、选择题6. D7. A8. B 解:因为(a -2)2+︱b +3︱=0,所以(a -2)2=0,︱b +3︱=0,所以a-2=0,b +3=0,所以a =2,b =-3 则(a +b )2008=(-3+2)2008=1.故选B .三、解答题9. (1)16-(2)81 (3)1 (4)1-(5)278-(6)8116 (7)2 (8)1-10. -9 9发现:不仅结果不同(互为相反数),而且两者意义,读法均不同.32-表示3的2次方的相反数,读作“3的2次方的相反数”或“负的3的2次方”;(-3)2表示(-3)的2次方,读作“负3的2次方”.11. 解:(1)(3×5)2=152 =22532×52 =9×25=225 所以(3×5)2 =32×52; 〔(-13×4)〕2=(-43)2=169 (-13)2×42=19×16=169所以〔(-13×4)〕2=(-13)2×42(2)(ab )3 = a 3b 3(3)当n 为正整数时,(ab )n = a n b n 说明如下:(ab )n =ab ·ab ·…·ab =(a ·a ·…·a ) ·(b ·b ·…·b )=a n b n n 个a n 个b方法小结:本题考查学生分析问题、总结、归纳、找规律的能力,这也是今后中考的一个热点问题.12. 2)n 321(⋯+++ 13. 1.44 0.0144 144小数点 左(右) 两位 14400 1440000 0.00000144 14.12×12×12×12×12=(12)5=132 所以,第五次跳起的高度是132米 15. 解:因为(x -1)2≥0 所以(x -1)2的最小值是0,所以当x =1时,式子(x -1)2=0 最小;式子42)1(--x =4-0=4 即最大值是4.。