【二分查找法】

二分查找算法经典题一、二分查找算法简介二分查找（Binary Search）是一种在有序数组中查找特定元素的搜索算法。

相较于全序查找，二分查找能够在时间复杂度上实现O(log n)的高效搜索。

该算法基于比较思想，通过不断缩小搜索范围来找到目标元素。

二、二分查找算法的应用场景1.有序数组查找：当数据集已经有序时，使用二分查找可以获得较快的搜索速度。

2.区间查找：在给定一个区间，寻找区间内的特定元素，如最大值、最小值等。

3.有序树查找：在二叉搜索树（BST）中进行查找操作。

三、经典二分查找题目解析1.题目一：有序数组查找特定元素给定一个有序数组，实现一个二分查找函数，找到目标元素的位置。

2.题目二：区间查找给定一个有序数组和一个小于数组平均值的值，找到该值在数组中的位置。

3.题目三：有序链表查找给定一个有序链表，实现一个二分查找函数，找到目标元素的位置。

四、实战案例与代码演示以下是一个使用Python实现的二分查找算法示例：```pythondef binary_search(arr, target):left, right = 0, len(arr) - 1while left <= right:mid = left + (right - left) // 2if arr[mid] == target:return midelif arr[mid] < target:left = mid + 1else:right = mid - 1return -1arr = [1, 3, 5, 7, 9, 11, 13, 15]target = 11print(binary_search(arr, target)) # 输出：4```五、优化与扩展1.线性时间复杂度优化：当数据集无序时，可以通过预处理数据实现有序化，从而将时间复杂度降低到O(n)。

2.外部排序：当数据集过大，无法一次性加载到内存中时，可以通过外部排序实现二分查找。

二分法查找1、二分查找(Binary Search)二分查找又称折半查找，它是一种效率较高的查找方法。

二分查找要求：线性表是有序表，即表中结点按关键字有序，并且要用向量作为表的存储结构。

不妨设有序表是递增有序的。

2、二分查找的基本思想二分查找的基本思想是：（设R[low..high]是当前的查找区间）（1）首先确定该区间的中点位置：（2）然后将待查的K值与R[mid].key比较：若相等，则查找成功并返回此位置，否则须确定新的查找区间，继续二分查找，具体方法如下：①若R[mid].key>K，则由表的有序性可知R[mid..n].keys均大于K，因此若表中存在关键字等于K的结点，则该结点必定是在位置mid左边的子表R[1..mid-1]中，故新的查找区间是左子表R[1..mid-1]。

②类似地，若R[mid].key<K，则要查找的K必在mid的右子表R[mid+1..n]中，即新的查找区间是右子表R[mid+1..n]。

下一次查找是针对新的查找区间进行的。

因此，从初始的查找区间R[1..n]开始，每经过一次与当前查找区间的中点位置上的结点关键字的比较，就可确定查找是否成功，不成功则当前的查找区间就缩小一半。

这一过程重复直至找到关键字为K的结点，或者直至当前的查找区间为空(即查找失败)时为止。

3、二分查找算法int BinSearch(SeqList R，KeyType K){ //在有序表R[1..n]中进行二分查找，成功时返回结点的位置，失败时返回零int low=1，high=n，mid；//置当前查找区间上、下界的初值while(low<=high){ //当前查找区间R[low..high]非空mid=(low+high)/2；if(R[mid].key==K) return mid；//查找成功返回if(R[mid].kdy>K)high=mid-1; //继续在R[low..mid-1]中查找elselow=mid+1；//继续在R[mid+1..high]中查找}return 0；//当low>high时表示查找区间为空，查找失败} //BinSeareh二分查找算法亦很容易给出其递归程序【参见练习】4、二分查找算法的执行过程设算法的输入实例中有序的关键字序列为(05，13，19，21，37，56，64，75，80，88，92)要查找的关键字K分别是21和85。

二分查找法的算法过程
二分查找法（Binary Search）是一种在有序数组中查找特定元素的算法。

它的算法思想是将数组分为两部分，然后判断目标元素与中间元素的大小关系，进而确定目标元素在哪一部分中，然后再在相应的部分中继续进行查找，直到找到目标元素或确定目标元素不存在。

具体的算法过程如下：
1. 首先，确定数组的起始位置（start）和结束位置（end）。

- start 初始化为数组的第一个元素的索引。

- end 初始化为数组的最后一个元素的索引。

2. 然后，计算出数组的中间位置（mid）。

- mid = (start + end) / 2。

3. 接下来，比较目标元素与中间元素的大小关系。

- 如果目标元素等于中间元素，那么返回中间元素的索引，表示找到了目标元素。

- 如果目标元素小于中间元素，说明目标元素在数组的前半部分，所以将结束位置 end 更新为 mid - 1。

- 如果目标元素大于中间元素，说明目标元素在数组的后半部分，所以将起始位置 start 更新为 mid + 1。

4. 然后，再次计算新的中间位置，并重复步骤 3，直到找到目标元素或确定目标元素不存在。

- 如果 start 大于 end，表示数组中不存在目标元素。

通过以上的算法过程，可以高效地在有序数组中查找目标元素。

二分查找法的时间复杂度为 O(log n)，其中 n 表示数组的长度。

它比线性查找等其他查找算法要更加高效，尤其适用于大规模数据的查找操作。

《二分查找法》作业设计方案（第一课时）一、作业目标本次作业旨在让学生掌握二分查找法的概念和原理，通过实践操作熟悉该算法的实现过程，提高学生的计算思维能力。

二、作业内容1. 完成一个简单的二分查找程序，用于在已排序的数组中查找指定元素。

程序应包括输入、判断、输出等基本步骤。

2. 针对不同的数组和元素，尝试使用二分查找法进行查找，并记录查找过程和结果。

3. 分析二分查找法的优点和适用范围，与其他查找算法进行比较。

三、作业要求1. 按照程序设计的规范，使用规定的编程语言（如Python）完成作业。

2. 提交完整的程序代码，并附上对程序的简要说明和讨论。

3. 作业应在规定时间内完成，时间限制为一周（48小时）。

4. 鼓励合作学习，可与同学组成小组共同解决问题。

四、作业评价1. 评价标准包括程序的正确性、完整性、简洁性和创新性。

2. 评价方式将采取教师评价与同学互评相结合的方式，重点评估学生在解决问题过程中的思考和表达能力。

3. 评价结果将作为学生平时成绩的一部分，记入期末总评。

五、作业反馈1. 学生提交作业后，教师将对作业进行审核，并及时反馈给学生，指出存在的问题和改进建议。

2. 学生可根据教师的反馈对作业进行修改和完善，以提高自己的编程能力和计算思维能力。

3. 同学之间的互评也可以促进相互学习和交流，提高学习效果。

六、附加任务：尝试使用二分查找法解决实际问题，如在一个未排序的数组中查找最大（小）值元素，或者在一个有序数组中查找特定范围内的元素。

这将有助于学生更好地理解二分查找法的应用场景和实际价值。

七、资源准备：1. 本次作业需要学生具备基本的编程知识和技能，建议在课前预习相关教材和资料。

2. 准备好规定的编程语言（如Python）和开发环境，确保能够顺利完成作业。

3. 准备好教师提供的参考示例代码，以便参考和学习。

八、作业提交方式：学生将作业提交至指定的平台或邮箱，教师将对学生作业进行批改和反馈。

作业设计方案（第二课时）一、作业目标通过本次作业，学生应熟练掌握二分查找法的应用，能够在实际问题中灵活运用该算法，提高数据搜索的效率。

二分查找算法详解
一、算法介绍
二分查找算法又称折半查找算法，是一种分治思想的算法。

它的思想是：将空间定义为一个有序数组中从左到右的递增区间，每次进行二分查
找的时候，可以将空间缩小一半。

首先，取有序数组的中间元素作为比较
的对象，如果查找的目标元素与此元素相等，则直接输出结果；如果查找
的目标元素大于中间元素，则将查找范围减小一半，从中间元素的右半部
分继续进行查找；如果查找的目标元素小于中间元素，则将查找范围减小
一半，从中间元素的左半部分继续进行查找；如此反复，直到找到要查找
的目标元素，或者没有找到目标元素为止。

因此，如果要查找的元素在有
序数组中，二分查找算法有最佳的效率，因此，它是一种快速算法。

二、算法描述
1、首先，为有序数组定义low、high指针，令low指向有序数组的
第一个元素，high指向有序数组的最后一个元素。

2、然后，取有序数组的中间元素mid（即low和high的中间位置），将mid元素与查找的目标元素target进行比较。

3、如果target等于mid元素，则查找成功，输出mid元素的下标；
4、如果target大于mid元素，则将空间范围缩小一半，把low设置
为mid+1，继续进行二分查找；。

二分查找算法是一种在有序数组中查找特定元素的高效算法。

在生活中，我们可以将二分查找算法应用于许多场景，以提高搜索效率。

以下是一些例子：
1. 字典查找：当我们使用字典查找一个单词的定义时，通常会从中间的页码开始查找。

如果所查找的单词在中间页码之前，则在字典的前半部分查找；如果在中间页码之后，则在字典的后半部分查找。

这种查找方式就是应用了二分查找算法。

2. 电话簿搜索：在电话簿中查找一个联系人时，我们可以先大致估计联系人姓名所在的位置，然后根据估计的位置进行查找。

如果找到了联系人，则搜索成功；如果没有找到，则根据姓名首字母在电话簿中的位置，判断联系人可能在前面或后面的部分，然后相应地缩小搜索范围。

这也是二分查找的一种应用。

3. 有序数据库查询：在数据库管理中，当我们需要根据特定关键字查询数据时，如果数据库中的数据是有序的，我们可以使用二分查找算法来加快查询速度。

例如，在电子商务网站中根据价格排序的商品列表中查找特定价格的商品。

4. 软件更新：在软件更新过程中，有时我们需要根据特定条件（如版本号）在大量更新文件中查找对应的更新包。

通过使用二分查找算法，我们可以快速定位到所需的更新文件，从而提高更新效率。

5. 排序比赛：在某些排序比赛中，参赛者需要根据特定的规则对一系列数据进行排序。

在这种情况下，参赛者可以使用二分查找算法来确定自己的排名，从而节省时间并提高效率。

总之，二分查找算法在生活中的许多场景中都有应用，它可以帮助我们更快地找到所需的信息，提高工作和生活的效率。

二分法查找数值
二分法查找数值
二分法，也叫二分查找，是一种在有序数组中查找特定元素的算法。

其基本思想是每次取数组中间的值与目标值进行比较，然后根据比较结果舍弃一半的数据，直到找到目标值或者发现目标值不存在为止。

二分法查找数值的具体步骤如下：
1. 初始化左右指针，left=0，right=n-1。

（n为数组长度）
2. 当left小于等于right时，进行以下操作：
3. 取中间值middle=(left+right)/2。

4. 如果中间值等于目标值，返回目标值的位置。

5. 如果中间值大于目标值，说明目标值在middle的左侧，将right更新为middle-1。

6. 如果中间值小于目标值，说明目标值在middle的右侧，将left更
新为middle+1。

7. 如果循环结束还没有找到目标值，说明目标值不存在，返回-1。

二分法的时间复杂度为O(logN)，是一种十分高效的查找算法，因此
在很多情况下都被广泛应用。

其中包括在数据量较大的有序数组中查
找特定元素，以及在游戏中对答案进行猜测等。

总之，二分法通过逐步缩小查找范围，可以快速高效地查找指定元素，是一种很实用的算法。

在实际使用时，需要注意的是数组必须是有序的，否则无法保证算法正确性。

同时，由于函数栈空间有限，在数据
量较大时需要注意是否会爆栈。

二分法算法二分法算法，也称为二分查找算法，是一种常用的查找算法。

它的基本思想是将已排序的数组分成两部分，然后通过比较目标值与数组中间元素的大小，来确定目标值可能存在的区域，然后再在这个区域内继续使用二分法查找。

这个过程不断重复，直到找到目标值或确定目标值不存在为止。

在开始之前，我们先来了解一下二分法算法的原理。

假设我们要在一个有序数组中查找目标值。

首先，我们取数组的中间元素，然后将目标值与中间元素进行比较。

如果目标值等于中间元素，那么就找到了目标值；如果目标值小于中间元素，那么目标值可能存在于数组的左半部分；如果目标值大于中间元素，那么目标值可能存在于数组的右半部分。

根据这个比较结果，我们可以将查找范围缩小一半，然后再在这个范围内继续使用二分法查找。

这个过程不断重复，直到找到目标值或确定目标值不存在为止。

二分法算法的时间复杂度是O(log n)，其中n为数组的大小。

这是因为每次查找都将查找范围缩小一半，所以最多需要进行log n次查找。

相比于简单的线性查找算法，二分法算法的效率更高。

但是二分法算法有一个前提条件，就是数组必须是有序的。

如果数组无序，那么需要先对数组进行排序，然后再使用二分法算法进行查找。

下面我们通过一个具体的例子来说明二分法算法的应用。

假设有一个有序数组arr，长度为n，我们要查找目标值target。

首先，我们可以设置两个指针left和right，分别指向数组的第一个元素和最后一个元素。

然后，我们计算出中间元素的索引mid，将中间元素与目标值进行比较。

如果中间元素等于目标值，那么就找到了目标值；如果中间元素大于目标值，那么目标值可能存在于数组的左半部分，我们将right指针更新为mid-1；如果中间元素小于目标值，那么目标值可能存在于数组的右半部分，我们将left指针更新为mid+1。

然后，我们继续在更新后的查找范围内使用二分法查找，直到找到目标值或确定目标值不存在为止。

二分法算法的应用场景有很多，比如在有序数组中查找目标值、在有序矩阵中查找目标值等。

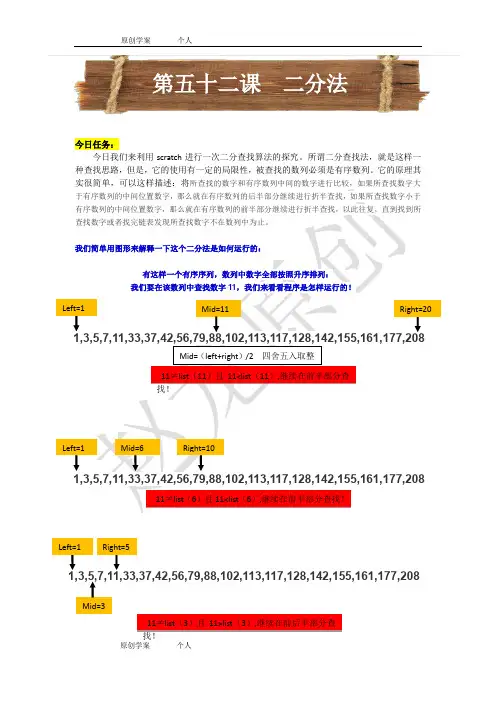
今日任务：今日我们来利用scratch进行一次二分查找算法的探究。

所谓二分查找法，就是这样一种查找思路，但是，它的使用有一定的局限性，被查找的数列必须是有序数列。

它的原理其Left=1 Right=51,3,5,7,11,33,37,42,56,79,88,102,113,117,128,142,155,161,177,208 Mid=311≠list（3）且11>list（3）,继续在前后半部分查找！Left=4 Right=51,3,5,7,11,33,37,42,56,79,88,102,113,117,128,142,155,161,177,208Mid=5 11=list（5），查找结束！返回列表位置5.如果是按照顺序查找法，需要查找5次，而用二分法只需要4次就可以查找到了，如果有序数列更复杂一些更长一些，二分法比顺序查找法的优势就更加明显！跟我来挑战Follow me：第一步：启动scratch软件；第二步：点击上方的“文件”→“保存”→保存到桌面，文件名：二分查找→点击“保存”；（第二步很很很重要，我希望所有的学生都能养成及时保存作品的好习惯！）第三步：首先我们先生成一个斐波那契数列程序较长，我们单独将二分法算法程序定义为一个单独地功能块（子程序），用的时候调用就可以了！还记得left 和right 、mid 分别是什么？再提醒一下！n=list(mid)最后直接调用这个功能块即可： 该程序的运行结果是：课后思考：（1） 试着总结一下二分法的优缺点？优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。

因此，折半查找方法适用于不经常变动而查找频繁的有序列表。

（2）想一想，二分查找法的用途有哪些？二分查找法是最省优查找算法吗？有没有更高效的算法处理有序数列？（3）自己尝试设计出一个随即有序数列，尝试用二分法去查找结果。

二分法查找
二分查找也称折半查找（Binary Search），是一种在有序数组中查找目标值的算法。

它的基本思想是将数组分为两部分，然后判断目标值可能存在的那一部分，并继续在该部分中进行查找，以此逐渐缩小查找范围，直到找到目标值或确定不存在。

二分查找的基本实现步骤如下：
1. 确定数组的左边界和右边界，初始时左边界为0，右边界为数组长度减1。

2. 计算数组的中间位置mid，可以使用公式mid = (left + right) / 2。

3. 比较中间位置的元素与目标值的大小关系：
- 如果中间位置的元素等于目标值，则找到目标值，返回中间位置。

- 如果中间位置的元素大于目标值，则目标值可能在左侧部分，更新右边界为mid - 1。

- 如果中间位置的元素小于目标值，则目标值可能在右侧部分，更新左边界为mid + 1。

二分查找虽然思路简单，但在实现过程中需要注意细节，如循环中的不等号是否应该带等号，mid是否应该加一等。

分析这些细节的差异以及出现这些差异的原因，有助于更加灵活准确地实现二分查找算法。

二分查找面试题在面试中，经常会遇到涉及算法和数据结构的问题。

而二分查找算法是其中常见的一种，被广泛应用于各种场景。

本文将介绍什么是二分查找算法，以及如何应对二分查找相关的面试题。

一、什么是二分查找算法二分查找算法，也称为折半查找算法，是一种针对有序数组的查找算法。

其核心思想是通过与数组的中间元素进行比较，然后确定待查找元素在左边还是右边，从而逐步缩小查找范围，最终找到目标元素或者确定目标元素不存在。

二分查找的基本流程如下：1. 确定数组的左边界left和右边界right，初始时left=0，right=n-1，其中n为数组长度。

2. 计算中间元素的下标mid，mid=(left+right)/2。

3. 比较中间元素与目标元素的大小关系：- 如果中间元素等于目标元素，返回中间元素的下标即为目标元素的位置。

- 如果中间元素大于目标元素，说明目标元素可能在左半部分，此时更新右边界right=mid-1。

- 如果中间元素小于目标元素，说明目标元素可能在右半部分，此时更新左边界left=mid+1。

4. 重复步骤2和步骤3，直到找到目标元素或者左边界大于右边界时搜索结束。

二、二分查找面试题下面我们将针对二分查找算法进行一些面试题的分析和解答。

1. 搜索旋转排序数组题目描述：给定一个经过旋转的有序数组，例如{4,5,6,7,0,1,2}，请在数组中搜索给定的目标元素，并返回它的下标。

如果目标元素不存在，返回-1。

解题思路：通过修改二分查找的判断条件，可以解决这道题。

具体步骤如下：- 比较左边界元素、中间元素和右边界元素的大小关系，判断目标元素可能在左半部分、右半部分还是中间部分。

- 根据判断的结果，更新左边界和右边界，然后再进行下一轮二分查找。

- 当左边界大于右边界时，搜索结束，返回-1。

2. 搜索插入位置题目描述：给定一个有序数组和一个目标值，如果目标值在数组中存在，则返回目标值的下标；如果目标值在数组中不存在，则返回它应该被插入的位置的下标。

二分法查找算法范文
二分查找，又称折半查找，是一种在有序数组中查找其中一特定元素的算法，它的最坏时间复杂度为O（log2n）。

二分查找比较容易理解和实现，但是对于非顺序表来说，要将其转换为有序表，这将消耗较大的空间和时间，所以它不适用于大规模数据集，而且它只适用于静态数据集，不适用于动态数据集。

二分查找算法的关键在于取数组中间位置的值，将数组分为两部分，中间那个值成为支点。

通过比较支点的值和查找的值，确定支点左右的数据范围，再根据支点位置和查找的值，将需要查找的范围缩小到一半，这样循环查找，直到被查找的数据被找到为止。

具体步骤如下：
（1）首先，从有序数组的中间位置开始查找，也就是数组中间的数据项。

（2）如果中间位置的数据项正好是被查找的数据，那么查找工作就完成了。

（3）如果中间位置的数据项大于被查找的数据，那么在数组的前半部分继续查找。

（4）如果中间位置的数据项小于被查找的数据，那么在数组的后半部分继续查找。

（5）重复步骤1到步骤4，直到被查找的数据被找到为止。

二分查找算法有以下优点：
1. 二分查找的时间复杂度是O(log2n)。

C语言二分查找算法及实现代码二分查找算法（Binary Search Algorithm）也被称为折半查找算法，是一种常见的查找算法。

它的原理是将有序数组（或有序列表）从中间划分为两部分，然后将待查找元素与中间元素进行比较，如果相等则返回元素的索引；如果待查找元素较大，则在右半部分继续查找；如果待查找元素较小，则在左半部分继续查找，直到找到目标元素或者确定目标元素不存在为止。

二分查找算法的时间复杂度为O(log n)，其中n是数组的长度。

相比于顺序查找算法的时间复杂度O(n)，二分查找算法具有更高的效率。

下面是用C语言实现二分查找算法的代码：```c#include <stdio.h>int binarySearch(int arr[], int left, int right, int target) while (left <= right)int mid = (left + right) / 2;if (arr[mid] == target)return mid;}else if (arr[mid] < target)left = mid + 1;elseright = mid - 1;}}return -1;int mai//假设有一个有序数组int arr[] = {2, 7, 14, 19, 26, 33, 41, 55, 68, 77}; int n = sizeof(arr) / sizeof(arr[0]); // 数组长度int target = 33; // 目标元素int result = binarySearch(arr, 0, n - 1, target); if (result == -1)printf("目标元素不存在\n");}elseprintf("目标元素的索引是%d\n", result);}return 0;以上代码中，binarySearch函数接收一个有序数组、左右索引和目标元素作为参数。

分治算法——二分查找法分治算法是一种将问题划分成多个独立的子问题来解决的算法思想，通常用于解决一些具有重复性的问题。

其中，二分查找法是分治算法的典型应用之一，被广泛应用于各种排序和查找问题中。

二分查找法，顾名思义，就是将要查找的元素不断与中间元素进行比较，然后根据比较结果来确定继续在哪个半区间进行查找，直到找到目标元素或者确定目标元素不存在为止。

二分查找法的前提是待查找的数组或列表必须是有序的。

具体的实现方法是，首先确定查找范围的起始位置和结束位置，然后求取中间位置的下标。

接下来，将待查找的元素与中间位置的元素进行比较，若相等，则直接返回中间位置；若待查找元素小于中间位置的元素，则继续在左半区间进行查找，即将查找范围的结束位置调整为中间位置的前一个位置；若待查找元素大于中间位置的元素，则继续在右半区间进行查找，即将查找范围的起始位置调整为中间位置的后一个位置。

然后重复上述过程，直到查找到目标元素或者确定目标元素不存在。

二分查找法的时间复杂度为O(logN)，其中N表示待查找的元素个数。

这是因为在每一次比较过程中，查找范围都会减半。

在最坏的情况下，即待查找的元素不在数组或列表中时，需要进行logN次比较才能确定。

二分查找法的应用非常广泛，特别是在查找和排序领域。

它可以用于在有序数组或列表中查找一些元素的位置，也可以用于确定一些元素是否存在于有序数组或列表中。

另外，二分查找法还可以用于解决其他一些问题，例如旋转排序数组、插入位置等。

尽管二分查找法的实现方法相对简单，但在具体应用时还需要注意一些细节问题。

首先，待查找的数组或列表必须是有序的，如果无序，则需要先进行排序。

其次，要注意查找范围的起始位置和结束位置的变化，以免出现越界访问的错误。

另外，如果数组或列表中存在相同的元素，需根据具体情况来确定返回的位置。

综上所述，二分查找法是一种高效的算法，适用于有序数组或列表的查找问题。

它的时间复杂度为O(logN)，在实际应用中极大地提高了效率。

【二分查找法】【二分查找法】二分查找又称折半查找，它是一种效率较高的查找方法。

【二分查找要求】：1.必须采用顺序存储结构 2.必须按关键字大小有序排列。

【优缺点】折半查找法的优点是比较次数少，查找速度快，平均性能好;其缺点是要求待查表为有序表，且插入删除比较困难。

因此，折半查找方法适用于不经常变动而查找频繁的有序列表。

【算法思想】首先，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。

重复以上过程，直到找到满足条件的记录，此时查找成功，或直到子表不存在为止，此时查找不成功。

二分查找又叫折半查找，但是有一个前提条件，就是你要查找的数据必须是按顺序储存，以关键字大小来排列的。

例如如果是整形数组，存放0~9这10个数，数组必须按0到9（升序）或者9到0（降序）挨个储存。

如果你数组的元素之字符串，字符串的首字母就得按a~z或者z~a挨个储存，当最高位相同时比较次高位。

当你保证数组有序后，就可以开始执行二分查找了。

举个例子1,3,6,8,9,10,11,15如果你要查找的数字是10，查找过程如下由于一共有7个元素，比较最中间的元素，即第四个，10>9，由于是升序排列，选择9的右边三个数进行比较,，这就将比较次数缩短了一半。

在右半部分再去中间元素，即11,10<11，选取11左边部分进行比较，即和10进行比较，得到要找的元素。

当然也存在找不到的情况，比如找12，先与9比，范围缩小至右半部分，跟11比，在此基础上再缩小至现有右半部分，只剩一个15，不相等，即没找到想要的元素。

这就是一个递归缩小范围的过程C语言代码int halfSearch(SeqList * R，int n , KeyType K ){ //在有序表R[0..n-1]中进行二分查找，成功时返回结点的位置，失败时返回-1int low=0，high=n-1，mid；//置当前查找区间上、下界的初值if(R[low].key==K){return 0 ;}while(low<=high){ //当前查找区间R[low..high]非空mid=low+((high-low)/2)；//使用(low + high) / 2 会有整数溢出的问题if(R[mid].key==K){return mid；//查找成功返回}if(R[mid].key>K)high=mid-1; //继续在R[low..mid-1]中查找elselow=mid+1；//继续在R[mid+1..high]中查找}return -1；//当low>high时表示查找区间为空，查找失败}Java代码：/*** 二分查找算法** @param srcArray 有序数组* @param target 被查找的元素* @return 找到元素target的数组下标，如果没有找到则返回-1 */public class Search {public static int halfSearch(int[] srcArray, int target){int low = 0;int high = srcArray.length-1;while(low <= high) {int middle = (low + high)/2;if(target == srcArray[middle]) {return middle;}else if(target <srcArray[middle]) {high = middle - 1;}else {low = middle + 1;}}return -1;}public static void main(String[] args){int[] src = new int[] {0,1, 3, 5, 7, 8, 9}; System.out.println(halfSearch(src, 8));//output 5 }}。

数据结构50：⼆分查找法（折半查找法）折半查找，也称⼆分查找，在某些情况下相⽐于顺序查找，使⽤折半查找算法的效率更⾼。

但是该算法的使⽤的前提是静态查找表中的数据必须是有序的。

例如，在{5,21,13,19,37,75,56,64,88 ,80,92}这个查找表使⽤折半查找算法查找数据之前，需要⾸先对该表中的数据按照所查的关键字进⾏排序：{5,13,19,21,37,56,64,75,80,88,92}。

在折半查找之前对查找表按照所查的关键字进⾏排序的意思是：若查找表中存储的数据元素含有多个关键字时，使⽤哪种关键字做折半查找，就需要提前以该关键字对所有数据进⾏排序。

折半查找算法对静态查找表{5,13,19,21,37,56,64,75,80,88,92}采⽤折半查找算法查找关键字为 21 的过程为：图 1 折半查找的过程（a）如上图 1 所⽰，指针 low 和 high 分别指向查找表的第⼀个关键字和最后⼀个关键字，指针 mid 指向处于 low 和 high 指针中间位置的关键字。

在查找的过程中每次都同 mid 指向的关键字进⾏⽐较，由于整个表中的数据是有序的，因此在⽐较之后就可以知道要查找的关键字的⼤致位置。

例如在查找关键字 21 时，⾸先同 56 作⽐较，由于21 < 56，⽽且这个查找表是按照升序进⾏排序的，所以可以判定如果静态查找表中有 21这个关键字，就⼀定存在于 low 和 mid 指向的区域中间。

因此，再次遍历时需要更新 high 指针和 mid 指针的位置，令 high 指针移动到 mid 指针的左侧⼀个位置上，同时令 mid 重新指向 low 指针和 high 指针的中间位置。

如图 2 所⽰：图 2 折半查找的过程（b）同样，⽤ 21 同 mid 指针指向的 19 作⽐较，19 < 21，所以可以判定 21 如果存在，肯定处于 mid 和 high 指向的区域中。

所以令 low 指向 mid 右侧⼀个位置上，同时更新 mid 的位置。

二分法逻辑
二分法也称为二分查找法，是一种在有序数组中查找目标值的算法。

基本逻辑如下：
1. 从有序数组的中间元素开始，将目标值与中间元素进行对比。

2. 如果目标值等于中间元素，则查找成功，返回该元素的索引。

3. 如果目标值小于中间元素，则在数组的左半部分继续进行二分查找。

4. 如果目标值大于中间元素，则在数组的右半部分继续进行二分查找。

5. 重复以上步骤，直到找到目标值或者数组的左边界大于右边界为止。

二分法的关键在于每次都将数组范围缩小一半，从而提高查找效率。

它的时间复杂度为O(logN)，其中N为数组的长度。

需要注意的是，二分法只适用于有序数组。

如果数组无序或者包含重复元素，就无法使用二分法进行查找。