北师大版八年级数学下册分式加减3导学案

数学初二下北师大版3.3分式的加减（1）导学案学习目标1.合作探究分式加减运算法那么的过程，理解公分母的意义,理解其算理。

2.掌握分母互为相反数的公分母的确定方法,会进行简单分式的加减运算,培养划归能力。

学习重点：同分母分式加减运算，学习难点：分母互为相反数的公分母的确定方法及其分式的加减运算。

【学前预备】独立完成以下预习作业：1、填空：15与35的相同，称为分数，15+35＝，法那么是；2，〔1〕同分母的分数如何加减？〔2〕b a 与c a的相同，称为分式；你认为该式应等于3、分式的加减法法那么同分数的加减法法那么类似同分母分式相加减，分母，把分子; 【预习自测】 计算：〔1〕374x x x -+＝＝〔2〕x x y ++y y x+＝＝【探究案】仿照课本81页例1完成以下各题：【一】自主学习：(1)34x x y y x y x y x y--++++＝＝〔2〕32b a -32a a＝＝【二】合作探究、展示点评〔1〕=---b a b b a a 〔2〕2222235y x x y x y x ---+ 【三】拓展提升:(1)2111x x x -+--〔2〕4322x y y x y y x++--(3)2433x x x +--- 【训练案】【一】【当堂检测】即用式子表示为：c b a c b c a ±=±1计算〔1〕x x x 11-+⑵13121+-+++b a b a b a 2.计算：372()1313a a -+-等于()(A)3713a -(B)3a -(C)-3a 〔D)3a【二】【课后作业】〔1〕nm n m n n m n n m ---+-+22 (2)你能独立思考完成该题目吗？a a a 5153-+。

２０16－201７学年八年级数学下册5.3.3 分式的加减法(３)导学案（无答案)(新版)北师大版编辑整理：尊敬的读者朋友们:这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(２016－２0１7学年八年级数学下册5.3．3 分式的加减法（3)导学案（无答案）（新版）北师大版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步,以下为2０１6－2017学年八年级数学下册5.３．3 分式的加减法(３）导学案(无答案）（新版)北师大版的全部内容。

5。

3。

３分式的加减法（3)【学习目标】1、经历探索异分母分式加减运算法则的过程。

2、能解决一些简单的实际问题。

【学习重点】异分母分式加减运算法则。

【学习难点】异分母分式加减运算法则。

【学习过程】 一、基础训练二、新课学习三、 课堂检测1、计算22b a b a b-++得（ ）A 、22a b b a b -++ B 、a b + C 、22a b a b++ D 、a b -2、计算111)1(+--a a a bcc b ab b a +-+)2(xxy x xy y -++1)1(11-2)2(-x 131)3(22--+-a a a a 111)1(+-+-n m n 31913)2(2+---+-a a a a a３、先化简，再求值: （1)已知时,求 的值（２)已知 ,求 的值四、课堂小结:这节课你有什么收获？ﻫ五、课后作业: 《练习册》A 本P38—39 六、教学反思:xx x --+-+31311)3(23321)4(-+-x xx x 222)5(nm m n m n n m m -++++101=aaa a a -+--+11112y x 3=yx yx y x xy -+--224以上就是本文的全部内容，可以编辑修改。

第五章 分式与分式方程5.3.3 分式的加减法【教学内容】熟练进行分式的加减运算。

【教学目标】知识与技能熟练进行分式的加减运算， 异分母的分式加减运算，引导学生总结运算方法和技巧，提高运算能力.过程与方法引导学生总结运算方法和技巧，提高运算能力.通过观察、分析、发展学生的逻辑推理能力。

情感、态度与价值观 让学生经历操作、实验、发现、确认等数学活动，引导学生总结运算方法和技巧，提高运算能力.体会数学观点，培养学生的数学意识。

【教学重难点】 重点：引导学生总结运算方法和技巧，提高运算能力.难点：理解并掌握异分母分式的加减运算.【导学过程】【知识回顾】同分母分式相加减 。

异分母分式相加减 。

【情景导入】计算：（1）226132abc a - (最简公分母是____ ） 解：原式=－ （通分：分母是最简公分母，写上分子） = （同分母的分式相加减）（2）yx y x -++11 (最简公分母是____ _) 解：原式= + （通分：分母是最简公分母，写上分子） = （同分母的分式相加减） = （注意化简运算结果为最简分式） 分式的混合运算题，要注意运算的顺序，先 ，后 ，有括号的要 。

【新知探究】探究一、合作探究11)1(2+-+y y y 计算： （2）4116142+---+-x x x x x探究二、已知的值。

求222,2yx y y x y y x x y x --+--=【知识梳理】1、异分母分式的加减法法则：异分母的分式相加减，先通分，化为______________的分式，然后再按同分母分式的加减法法则进行计算。

2、分式的混合运算： 与分数的加、减、乘、除混合运算一样，分式的加、减、乘、除混合运算，也是先算乘除，后算加减，遇有括号，先算括号内的。

3、确定最简公分母的一般步骤：①取各分母的_________的最小公倍数；②凡出现的字母（或含有字母的式子）的幂的因式都要取；③相同字母（或含有字母的式子）的幂的因式取__________________的；④如果分母是多项式，一般应先__________________________________。

(2) 5.3分式的加减法导学案（三）学习目标:1、 熟练地掌握异分母分式的加减运算、分式与整式的加减运算2、 能进行较复杂的异分母分式的加减运算一、复习旧知识：同分母分式是怎样进行加减运算的？异分母分式呢？1同分母的分式相加减，分母 ，把分子 __________ .2异分母分式相加减，先 _____________ 化为 ____________ ，然后再按 _______ 计算. 你掌握了哪些通分的方法 ？1）通分的方法是先求各分式的 _____________ 然后用 ________________ 除这个最简 公分母，用所得的商去乘 ________________ 02）最简公分母：最简公分母是各分母 __________ 的最高次幕的积，当分母的系数都 是整数时，取这些系数的 __________ 作为最简公分母的系数二、基础训练：练一练三、小组合作，小组展示:个小组自由讨论，交流，然后上台展示小组成果 例1:计算y 1(1)」 —— xy x xy _ x 四练习巩固1计算：a 2 -11分式2x 和「的最简公分母是（ 一）；2x x -1和&的最简公分母是（4 1 (1)-r -; a a(3) ab b c be2例2:已知' =2，亠_丄_飞^的值.y x_y x+y x_y 五学以致用（2）、已知 x =3y,求 2 2 x -y -x y 的值 x -y 六随堂练习1、先化简，再求值1 a +11已知a 二——，一- a 1的值 10 a -1 1 - a （1）x -2 2 计算：（1）bH1 a 1⑵ab^ + a 2 -b 2 m n m「n 2m 2 ~2 2 m -n七直击中考其中a -3-d.（2016广东）先化简，再求值:a 3 6 2a-6a a2 6a 9 a2 - 9。

§ 5.3《分式的加减法》(第一课时)导学案【学习目标】1.根据回忆同分母分数的加减法法则，经历探索同分母的分式加减法法则的过程, 掌握分式加减法法则。

2. 会进行简单同分母分式的加减运算及分母互为相反式的分式加减法运算.【教学重点】理解同分母的分式加减法的运算法则，能进行同分母的分式加减运算.【教学难点】分母互为相反数的分式加减法运算.【学习过程】【第一环节：复习回顾】1、_________________________________________________________ 什么是分式？2、当x 时，分式二二0---------------- x+23、若分式、一亠-出・二0,那么x的值是x2-l -------------------------4、 (a—b)=____ (b —a) (a—b) 2=_(b—a) 2 (填“ + ” 或“―”)【第二环节：探究新知】(学习目标1)计算下列各题：(1) (2) (3) (4)同分母分数的加减法法则归纳： _______________________________________2.计算：分式的加减法的实质与分数的加减法相同，你能说出分式的加减法法则?同分母分式的加减法法则归纳： ___________________________________________目标达成11 •计算——的结果是( )A.'a a a 2•计算的结果是( )A.a-b a-53•化简冬-县的结果是( )A.m-34•计算.：，结果是( )A. 0x-1 x-1【第三环节：例题讲解】(学习目标2)例1 (1)…•殳艺;ab abB. ■-C."D.亠1 B.-1C. 0 D. a —5m+3 B.m —3 C.Dirrl-3m-3 B. 1 C.-1 D. x(2) 2x 4 .目标达成2例2计算（学习目标2）(1) x y；x-y x-y(2) (1 _2a丿a—1 1 -a(3) m -2n 4m nm n m n(4)x 2 x -1 x -3----- —----- +-------x 1 x 1 x 1目标达成2(1) 2a2a —bb•(2) 2x-1x-1 1 -xb -2a '(3)m 2n nn「m m「n2nn「mm -1 x n -m a22ab - b2----- +------------a b a bx _2y 7x y2x - y 2x - y。

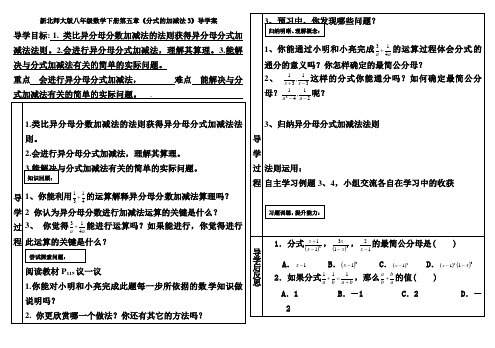
新北师大版八年级数学下册第五章《分式的加减法3》导学案导学目标: 1.类比异分母分数加减法的法则获得异分母分式加减法法则。

2.会进行异分母分式加减法，理解其算理。

3.能解决与分式加减法有关的简单的实际问题。

重点会进行异分母分式加减法，难点能解决与分式加减法有关的简单的实际问题。

.导学过程1.类比异分母分数加减法的法则获得异分母分式加减法法则。

2.会进行异分母分式加减法，理解其算理。

3.能解决与分式加减法有关的简单的实际问题。

1、你能利用4131+的运算解释异分母分数加减法算理吗？2 你认为异分母分数进行加减法运算的关键是什么？3、你觉得aa413+能进行运算吗？如果能进行，你觉得进行此运算的关键是什么？阅读教材P119议一议1.你能对小明和小亮完成此题每一步所依据的数学知识做说明吗？2. 你更欣赏哪一个做法？你还有其它的方法吗？导学过程导学后反思3、预习中，你发现哪些问题？1、你能通过小明和小亮完成aa413+的运算过程体会分式的通分的意义吗？你怎样确定的最简公分母？[来源:Z。

xx。

]2、31,31-+xx这样的分式你能通分吗？如何确定最简公分母？21,412--aa呢？3、归纳异分母分式加减法法则法则运用：自主学习例题3、4，小组交流各自在学习中的收获1．分式()211-+xx，()313xx-，12-x的最简公分母是( )[来源:Z&xx&]A．1-x B．()31-x C．()21-x D．()21-x()31x-2．如果分式baba+=+111，那么abba+的值( )A．1 B．－1 C．2 D．－2知识回顾：尝试探索问题：归纳明晰、理解概念：习题训练，提升能力：3．若xx 1=，则分式36224+-+x x x 的值为( )A ．0B ． 1C ．－1D ．－24．已知311=-yx ，则y xy x y xy x ---+55的值为 ． 5．若ab ＝１，则11+++b ba a 的值为 ．6．计算：（1）112---x x x （2）4412222+----+x x x xx x（3）)11)(2xy x x xy -+-（ （4）（x －1－18+x ）÷13++x x教学反思：[来源:学科网][来源:Z#xx#]。

八年级数学下册《分式的加减》导学案（2）北师大版（二）自学导读学习目标1、熟练掌握异分母分式的加减法;2、明确分式混合运算的顺序;3、熟练地进行分式的混合运算、重点：熟练地进行分式的混合运算、难点：熟练地进行分式的混合运算、读书思考1、回顾异分母分数的加减法：异分母分数相加减,先 ,化为分数,然后按照的加减法则进行计算、2、认真阅读P82-83的内容，回答:异分母分式的加减法则是什么?探究1:计算分析:本题中的两个分式的分母都是多项式,它们的分母分别是 ,能分解因式的是 ,将它分解因式为 ;选取它们的公分母是 ;两个分式通分后分别为、请你写出完整的计算过程解:思考:当相加减的分式的分母为多项式时,要先 ,再确定 ,进行通分,然后按照同分母分式的加减法则进行计算、探究2:甲乙两名采购员同去一家饲料公司两次购买饲料,两次饲料的价格分别为m元/千克和n元/千克（m、n为正数，m≠n），两名采购员的购买方式不同，其中甲每次买1000千克，乙每次用去元。

求甲乙所购饮料的平均价格是多少？（要想求出平均价格，应先知道哪些量）归纳小结异分母分式的加减法法则是什么? 练习巩固1、下列计算正确的是 ( )A B C D2、计算通过本节课的学习,我们知道了:1、异分母分式的加减法则;2、各分母的系数都是整数时通常取它们的系数的作为最简化分母的系数;凡是在各个分母中出现的字母(或式子)取其指数最大值作为最简化分母的一个因式;当分母是多项式时,应先 ,再确定最简公分母、课后巩固达标测试1、计算的结果正确的是 ( )A 0 B C D2、的最简公分母是 ;3、 ,则m= ;4、化简的结果是；5、计算：6、甲乙两港分别位于长江的上下游，相距skm一艘游轮往返其间，如果游轮在静水中的速度是akm/h,水流速度是bkm/h，求该游轮往返两港一趟所需的时间？这节课你学会了什么？还有什么疑问？。

§3.3. 分式的加减法（二）一、导学目标：（一）教学知识点：1.异分母的分式加减法的法则.2.分式的通分.（二）能力训练要求：1.经历异分母分式的加减运算和通分的过程，训练学生的分式运算能力，培养数学学习中转化未知问题为已知问题的能力.2.进一步通过实例发展学生的符号感.（三）情感与价值观要求：1.在学生已有数学经验的基础上，探求新知，从而获得成功的快乐.2.提高学生“用数学”意识.二、导学重点：1.掌握异分母的分式加减运算. 2.理解通分的意义.三、导学难点：1.化异分母分式为同分母分式的过程. 2.符号法则、去括号法则的应用.四、导学方法：启发、探索相结合五、导学设计：（一）温故：补充练习计算：（1）9122-m +m -32; （2）a +2－a -24. （3）11-a －212a-（四）拓展： 一、请你填一填（1）异分母分式相加减，先________变为________分式，然后再加减. （2）分式xy 2,y x +3,yx -4的最简公分母是________.（3）计算：222321xyz z xy yz x +-=_____________.（4）计算：)11(1xx x x -+-=_____________ （5）.如果x ＜y ＜0，那么xx ||+xy xy ||化简结果为____________. .二、判断题（1）a b a b a a b a a b a --+=--+=0（ ） （2）11)1(1)1(1)1()1(1)1(22222-=--=---=-+-x x x x x x x x x （ ） （3）)(2121212222y x y x +=+（ ） （4）222b a c b a c b a c +=-++（ ） 三、认真选一选（1）如果x ＞y ＞0,那么x y x y -++11的值是（ ） A.零 B.正数 C.负数 D.整数（2）甲、乙两人分别从相距8千米的两地同时出发，若同向而行，则t 1小时后，快者追上慢者；若相向而行，则t 2小时后，两人相遇，那么快者速度是慢者速度的（ ）A.211t t t +B.121t t t +C.2121t t t t +-D.2121t t t t -+ 四、请你来运算1.化简（1）（21222---+x x x x ）÷x 2 （2）13112-+-+x x x ·341222+++-x x x x（3）))((1))((1))((1b c a c ca b c b bc a b a a --++--++--+2.化简求值当x =21时，求1121122-+-++-x x x x x 的值.五、解答题1.计算： (3)232323194322---+--+x x x x x(4)(x +1－13-x )÷222-+x x2.化简求值： (2+1111+--a a )÷(a －21a a-)其中a =2.3.已知b a b a +-=+411，求b aa b+的值. 六、活动与探究：若)1)(1(3-+-x x x =1+x A +1-x B ，求A 、B 的值.。

知识像烛光，能照亮一个人，也能照亮无数的人。

--培根1 /2 §5.3.3分式的加减法（三）（P122～P124）第55课时 主备人： 审核人： 学科组审核：________教导处审核：_______学习目标（1）准确进行异分母分式的加减运算，理解简单的分式混合运算。

（2）能解决一些与分式的加减有关的简单实际问题，体会分式模型的作用。

学习重难点重点：熟练准确进行异分母分式的加减运算；难点：解决一些与分式的加减有关的简单实际问题。

学习过程一、自主预习1．同分母的分式相加减__________________________，用式子表示则为a c ±b c=______． 2．什么叫通分？通分的关键是什么？什么叫最简公分母？通分的作用是什么？3．异分母的分式相加减法，先 ，然后再 。

4. 请同学们预习作业教材P122～P124的内容，完成课本“做一做”（修1120米盲道…）二、自主探究，合作交流活动1：议一议：下面的3道题该怎样做？你会吗？请与小组成员交流你的想法。

计算1(1)y xy x xy x ++− 2(2)11x x x −++ 211(3)393a a a a a −+−−−+活动2：做一做： 计算①329122−−−m m ②2111x x ++− ③111x −=−活动3：例题点拨：已知 2x y=，222x y y x y x y x y −−−+−的值.知识像烛光，能照亮一个人，也能照亮无数的人。

--培根2 / 2 三、自我诊断，当堂训练1．计算1122−−−x x x 的正确结果是( ) A ．1+x B ．112−+x x C ．11−x D ．1−x 2.计算：（1）22639x x −−− （2）12332x x x x −+−3．计算：421444122++−−+−a a a a a ，其中3=a ．四、课堂小结五、课外拓展你知道有理数的混合运算顺序吗？如果是分式的混合运算，你将会怎样做？1.计算：（1）x x x x x x x x −÷+−−−−+4)44122(22（注意运算的结果要是最简分式）.2．计算：(1) x x x x x 22)242(2+÷−+− （2）)11()(ba ab b b a a −÷−−−六、学习/教学心得_______________________________________________________________________________。

八年级数学下册5.3 分式的加减法（第1课时）导学案（新版）北师大版学生活动经验基础：在相关知识的学习过程中，学生经历过许多类比和猜测的活动，如实数的加减运算类比整式的合并同类项；由在时的值的情况去猜测时的情况，由正整数相乘去发现规律猜测与负整数的乘法等，这些活动经验都为本节学习有很好的启迪。

【学习目标】课标要求：同分母分式的加减法是最简单的，也是学习异分母的分式加减的基础，所以作为起始节也是工具节内容，它就要求教学时务必使学生理解它并且能够灵活运用，对分母互为相反式的分式加减，能明白改变运算符号的实质。

因此，本节课的教学目标定位为：1、类比同分数加减法的法则归纳出同分母分式的加减法法则。

2、理解同分母的分式加减法的运算法则，能进行同分母的分式加减及分母互为相反式的分式加减法运算。

3、通过学习认识到数与式的联系，理解事物拓延的内在本质，丰富数学情感与思想。

本节课设计了6个教学环节：情景引入同分母加减练习巩固拓展提高课堂小结布置作业情景引入活动内容做一做：猜一猜活动目的：通过做一做的几道同分母分数加减的题，引导学生用类比的思想，猜一猜同分母分式的加减运算，并试图让学生认识其合理性。

从而抛出同分母分式加减法的运算法则，点明本节课的主要内容。

活动的注意事项：通过人人都可以入手的做一做，让学生回答，可以使学生很快进入状态又不觉得困难。

而后两个运算后要约分，学生极有可能报出没有约分的答案。

因此，类比时注意引导学生，正确猜想，约分是分数的必要步骤哦，使法则的提出顺理成章，也为后面的学习做好铺垫。

【自学导航】运算法则：同分母的分式相加减，分母不变，把分子相加减、用式子表示为：【合作探究】活动内容学习了同分母分式加减法的法则，是否会用还得先讲再练：例1（1）；（2）；（3）；（4）、活动目的：教学生如何运用法则进行运算，通过这4道例题，让学生学会加减法运算并注意运算时可能出现的问题。

活动的注意事项：在进行运算时若分子是多项式的，分子要先带括号，再去括号后合并同类项；运算结果也类比分数加减法的结果，要化成最简形式，即约去分子与分母的所练习巩固活动内容练一练(1); (2) ; (3);活动目的:通过3道题的演练巩固，让学生对同分母分式的加减法有更好的认识与掌握。