均匀平面电磁波的特性与特征参量
- 格式:ppt
- 大小:809.00 KB
- 文档页数:13





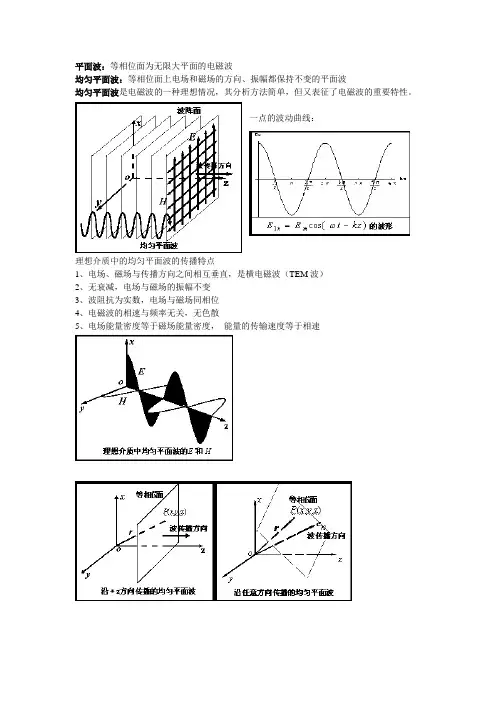
平面波:等相位面为无限大平面的电磁波
均匀平面波:等相位面上电场和磁场的方向、振幅都保持不变的平面波
均匀平面波是电磁波的一种理想情况,其分析方法简单,但又表征了电磁波的重要特性。
一点的波动曲线:
理想介质中的均匀平面波的传播特点
1、电场、磁场与传播方向之间相互垂直,是横电磁波(TEM波)
2、无衰减,电场与磁场的振幅不变
3、波阻抗为实数,电场与磁场同相位
4、电磁波的相速与频率无关,无色散
5、电场能量密度等于磁场能量密度,能量的传输速度等于相速。



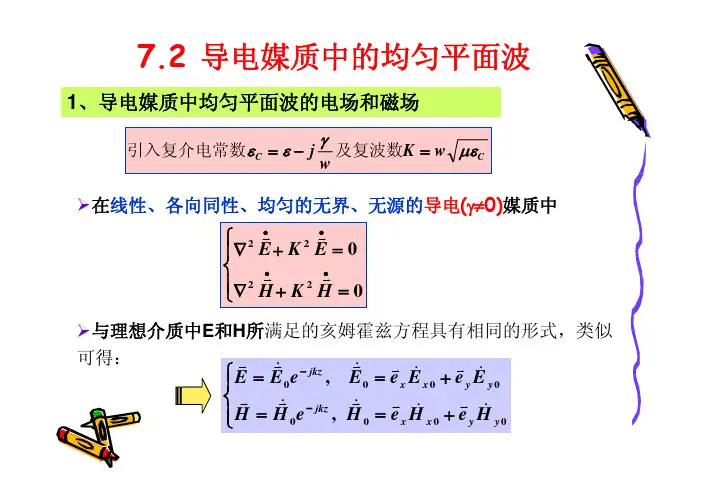
7.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性3)媒质导电性对场的影响媒质的导电性由比值 γ < 10 2 wε 1/ 2 γ γ Q K = w με c = w με 1 j ≈ w με 1 j wε 2 wε γ 决定,不仅与媒质特性有关,还与频率有关 wε(1)良介质μ μ γ = ηc = 1 j εc ε wε 1 / 2≈μ γ 1+ j ε 2 wε γ μ 1 , β ≈ w με , V p ≈ α ≈ 2 ε με 1 μ γ μ λ ≈ f με , η c = ε 1 + j 2 wε ≈ ε 平面波在良介质中的传播特性与理想介质中的平面波十分相似 只有微弱损耗引起的衰减,E和H时间相位差极小近似为07.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性(1)良导体γ Q K = w με c = w με 1 j wε γ > 100 wε1/ 2γ ≈ w με j 2 wε 1/ 2= wμγ e jπ / 4 = (1 j ) j2 γ = w με e 2 wε wμγπ1/ 22μ μ γ = ηc = 1 j εc ε wε 1 / 2μ γ ≈ j ε wε 1 / 2≈wμγejπ4= (1 + j )wμ 2γ7.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性 πf wμγ w 2w Vp = ≈ α≈β ≈ = πfμγ , =2 μγ β μγ 2 wμ j π wμ 2 π λ = 2π ≈ 2π 4 e = (1 + j ) , ηC = =2 wμγ fμγ β γ 2γ 良导体中,均匀平面波为色散波γ越大,电磁波的传播速度越慢,波长越短f=465MHz的电磁波在铜(γ=6.8×107s/m)中传播,其相速为 283.15m/s,波长为0.018mm电场相位超前磁场相位π/4, |ηc|<<1 wm>>we, 平均功率流密度沿波的传播方向按指数规律e-2αz衰减,而场的振幅 按e-αz衰减, γ越大衰减越快(趋肤效应)v 1 v v * v 1 2 γ 2αz Sc = E × H = ez E0 e (1 + j ) 2 2 2 μwv 1 2 γ 2αz S av = e z E 0 e 2 2 μw7.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性例7-2-1 有一均匀平面波,在海水中(εr=80,μr=1,γ=4s/m),v v 7 沿+z方向传播,在z=0处,E = e x 100 cos 10 π t(2)确定E的振幅衰减为z=0处的1%时的z值;() (V / m )(1)求其衰减常数α,相位常数β,相速Vp,波长λ及波阻抗ηc; (3)写出E(z,t)和H(z,t)在z=0.8m处的函数表示式分 析:v v Q E (z = 0 , t ) = e x 100 cos 10 7 π t() w = 10 7 πγ γ 4 = = = 180 > 100,为良导体 1 w ε w ε 0ε r 107 π × 10 9 × 80 36πwμγ 107 π × 4π × 10 7 × 4 (1)α ≈ β ≈ = = 8.89 ( Np / m ) 2 2 2π 2π w 107 π = = 0.707(m ) λ= Vp = = = 3.53 × 10 6 (m / s ) β 8.89 β 8.89ηC =wμγejπ4π j 107 π × 4π × 10-7 j π = e 4 = πe 4 (Ω ) 47.2 导电介质中的均匀平面波——2、导电媒质中均匀平面波的传播特性(2)波的振幅按 e αz 规律衰减,设 z = z1处,波的振幅衰减为 z = 0处的1%e( 3)α v v Q E (z = 0 , t ) = e x 100 cos 10 7 π t v v E (z , t ) = e x 100 e α z cos 10 7 π t - β z v v 100 α z H (z , t ) = e y e cos 10 7 π t - β z - θ , η c = η c e jθ αz1= 0.01 z1 = ln 0.01=ηc( ( (4.605 = 0.518(m ) 8.89)))v v (z = 0 .8 , t ) = e x 100 e 8 .89 × 0 .8 cos 10 7 π t - 8 .89 × 0 .8 ∴E v 082 = e x 0。

第一章第6讲Wave OpticsWave Optics132回 1.3.2电磁波的矢量性质分析:按一定的规顾电磁波是由高频振荡的电场E 和磁场B按定的规律随空间坐标r 和时间t 传播而形成的。
电磁波的波函数描的变化规律在一般情况下述了E 、B 随r 、t 的变化规律。
在般情况下,E 、B 的大小和方向均随r 、t 的变化而变化,总是发生在垂直波传播方向的平面内(横波)方向的平面内(横波)。
结论EBDH等描述电磁波性质的物理量必须用结论:E、B、D、H等描述电磁波性质的物理量必须用矢量来表示,即电磁波是矢量波。
回矢量分解顾xyE yE x−=)](exp[),()](exp[),(0000y y y x x x t kz j E t z E t kz j E t z E ϕωϕω+−=+14回§1.4电磁波在两种均匀各向同性透明媒质界面上的反射和折射研究的内容:顾电磁波在两种均匀的各向同性的透明媒质界面传播时,会发生反射、折射现象,讨论两种介质中的电磁波(入、反、透)之间在研究的方法:传播方向、能量、位相、振动方向等之间的关系。
研究的方法9从麦克斯韦方程组出发边界条件导出折、反射定律和菲涅耳公式9只讨论入、反、折射的电场波之间的关系只讨反折射的场波间的关系9以简谐平面波为研究对象122E dl E l E l R∴⋅=⋅+⋅+u v v u v u v u v≈E E l −⋅u v u v v横跨界面的矩形积分域1C∫ 212()忽略短边212()0E E l ∴−⋅=u v u v v 结论:结论2122()()E E l l −⊥−−u v u v v vu v u v v v u v u v可为平行于界面的任意方向21212211()//()0cos cos E E u u E E E E θθ⇒×==或在界面两侧,电场强度E的切向分量连续。
2.磁场的边界条件B u v0(13)AB ds ⋅=−∫∫积分域设为横跨界面的小扁盒的整个表面。
6.2 均匀平面电磁波的概念和特性1、均匀平面电磁波的概念2、时变电磁场的波动方程3、均匀平面波的特性在自由空间,麦克斯韦方程:EH t HE tεμ∂∇⨯=∂∂∇⨯=-∂c v 0,0==J ρ可见:时变的电场可以产生时变的磁场,时变的磁场又可以产生时变的磁电场,同时在空间上向邻近点推移,这样就产生了以一定速度向前传播的电磁波动。
该电磁波动称为电磁波。
什么是电磁波?例如:水波问题:一个点源所发射的电磁波的等相位面是什么样?1、均匀平面电磁波的概念(1)等相位面:在某一时刻,空间具有相同相位的点构成的面称为等相位面。
等相位面又称为波阵面。
(2)球面波:等相位面是球面的电磁波称为球面波。
(3)平面波:等相位面是平面的电磁波称为平面电磁波。
(4)均匀平面电磁波:任意时刻,如果在平面等相位面上,每一点的电场强度均相同,这种电磁波称为均匀平面电磁波。
2、时变电磁场的波动方程从麦克斯韦方程出发:c v 0∂∇⨯=+∂∂∇⨯=-∂∇⋅=∇⋅=DH J t BE tD B ρ在自由空间:HB E D με==0=⋅∇=⋅∇∂∂-=⨯∇∂∂=⨯∇H E tH E t E Hμεc v 0,0==J ρ对第一方程两边取旋度:)(E t H ⨯∇∂∂=⨯∇⨯∇ε()H t t εμ∂∂=-∂∂22Htμε∂=-∂根据矢量运算:22()H H H H∇⨯∇⨯=∇∇⋅-∇=-∇由此可得:222tH H ∂∂=∇με——磁场的波动方程同理可得:222tE E ∂∂=∇με——电场的波动方程3、均匀平面波的特性x yzO对均匀平面波而言,在直角坐标系,假设电磁波沿z 方向传播,等相位面平面平行于xOy 平面。
如图所示:0,0=∂∂=∂∂yx所以:22222222HH z t E Ez tμεμε∂∂=∂∂∂∂=∂∂(1)均匀平面波满足一维波动方程。
(2)均匀平面波是横电磁波(TEM 波)根据麦克斯韦第一方程:tE H ∂∂=⨯∇ε结论:电场只有E x 和E y 分量,说明电场矢量位于xOy 平面上。
均匀平面电磁波1. 引言均匀平面电磁波是一种具有特定频率的电磁辐射,它在空间中以均匀、平面波的形式传播。
电磁波是由变化的电场和磁场相互作用而产生的,具有广泛的应用领域,如通信、雷达、无线电和光学等。
本文将介绍均匀平面电磁波的定义、性质以及其在实际应用中的重要性。
2. 定义均匀平面电磁波是指在空间中以均匀且平行于波前传播的电磁辐射。
它具有以下特点: - 波动方向与传播方向垂直; - 电场和磁场强度在空间中保持恒定; - 波动速度等于光速。
3. 公式表示根据麦克斯韦方程组,可以得到均匀平面电磁波的数学表达式:E⃗=E0⃗⃗⃗⃗ sin(ωt−k⃗⋅r )B⃗ =k⃗ω×E⃗其中,E⃗和B⃗ 分别表示电场和磁场的矢量,E0⃗⃗⃗⃗ 表示电场的最大振幅,ω表示角频率,k⃗表示波矢,r表示位置矢量。
根据上述公式可以看出,均匀平面电磁波是一种正弦函数形式的波动。
电场和磁场之间存在相位差,并且沿着传播方向呈现出周期性变化。
4. 性质4.1 极化状态均匀平面电磁波可以具有不同的极化状态,包括线偏振、圆偏振和不偏振三种情况。
- 线偏振:电场方向在一个平面内振动,可以沿着任意方向进行观测。
- 圆偏振:电场方向在一个平面内以圆轨迹进行振动。
- 不偏振:电场方向在各个方向都有均匀分布,无特定的偏振状态。
4.2 传播特性均匀平面电磁波在空间中以光速传播。
由于其传播速度恒定且与介质无关,因此不会发生衍射和折射现象。
这使得电磁波在通信、雷达等领域中具有重要意义。
4.3 能量传输均匀平面电磁波通过电场和磁场之间的相互作用传输能量。
其能量密度与电场和磁场强度的平方成正比,即U∝E2。
能量的传输方向与波动方向相同。
4.4 反射和折射当均匀平面电磁波遇到边界时,会发生反射和折射现象。
根据入射角和介质的折射率,可以计算出反射角和折射角。
5. 应用均匀平面电磁波在现代科技中具有广泛的应用。
- 通信:无线电、移动通信、卫星通信等都是基于均匀平面电磁波的传输原理。