下载文档原格式
第八章绕流运动一、应用背景1、问题的广泛存在性：在自然界和工程实际中，存在着大量的流体绕物体的流动问题（绕流问题），如：飞机在空气中的飞行、河水流过桥墩、大型建筑物周围的空气流动、植物护岸（消浪，船行波），粉尘颗粒在空气中的飞扬和沉降，水处理中固体颗粒污染物在水中的运动。
（一种：流体运动；另外一种：物体运动），我们研究，将坐标系固结于物体上，将物体看成静止的，讨论流体相对于物体的运动。
2、问题的复杂性上一章的内容中可以看出，流体力学的问题可以归结为求解在一定边界条件和初始条件下偏微分方程组的求解。
但描述液体运动的方程式非常复杂的：一方面，是方程的非线性性质，造成方程求解的困难；另一方面，复杂的边界条件和初始条件都给求解流体力学造成了很多麻烦。
迄今为止，只有很少数的问题得到了解决。
平面泊萧叶流动，圆管coutte流动等等。
而我们所要解决的绕流问题正是有着非常复杂的边界条件。
3、问题的简化及其合理性流体力学对此的简化则是，简化原方程，建立研究理想液体的势流理论。
实际液体满足势流运动的条件：粘性不占主导地位，或者粘性还没有开始起作用。
正例：远离边界层的流体绕流运动、地下水运动、波浪运动、物体落入静止水体中，水的运动规律研究。
反例：研究阻力规律、能量损失、内能转换等等。
圆柱绕流（经典之一）半无限长平板绕流（经典之二）分成两个区域：一个区域是远离边界的地方，此区域剪切作用不明显，而且流体惯性力的影响远远大于粘性力的影响（理想液体）（引导n-s方程）；另一个是靠近边界的地方（附面层，粘性底层），此区域有很强烈的剪切作用，粘性力的影响超强，据现代流体力学的研究表明，此区域是产生湍流的重要区域，有强烈的剪切涡结构，但此区域只有非常薄的厚度。
此区域对绕流物体的阻力、能量耗损、扩散、传热传质都产生重要影响。
4、本章的主要研究内容（1） 外部：理想液体，（简化方法，求解方式）、（2） 内部：附面层理论，（简化方法，求解方式，求解内容，现象描述） （3） 两者的衔接。
Chapter 9-1 粘性不可压缩流体流动§1概述一、粘性不可压缩流动模型１、关于粘性 粘性摩擦的存在必导致绕流阻力的存在，运动的衰减及涡量的扩散。
在大e R 数下，惯性力>>粘性力，采用理想流体模型，理想流体理论对不脱体绕流情况下的升力，压力分布和速度分布给出了符合实际的结果，但在阻力等与粘性效应相关的问题上却无能为力。
因而，在研究阻力等起源于粘性的现象时须抛弃理想流体假设。
在小e R 数和中e R 数情况下，粘性作用不可忽略。
2、关于不可压缩流动（流体的压缩性对流动的影响可略）液体压缩系数小，一般可认为不可压缩（极端情况如激波等除外）。
气体在低速运动（速度远小于声速）、非定常时速度变化缓慢，且重力方向上流场的尺度<10km 时，可略其压缩性。
（当研究对流层（~10km ）内大气运动时，不能忽略重力场引起的压缩效应）。
３、基本方程组和边界条件均质不可压缩流体.const ρ=，且温度变化小，const μ=，故有20V dV pF V dt γρ⎫∇⋅=⎪⎬∇=-+∇⎪⎭求速度和压力场的完备方程组。
能量方程22:dUk T S S dtρμ=∇+ 用于求温度场 本构方程 2P p I S μ=-+ 用于求应力边界条件：在固壁表面上，流体的法向和切向速度分别等于固体表面的对应速度分量。
在自由表面上，0, 0nn n p p p τ=-=。
二、粘性流动分类，求解问题的几种途径层流：流体运动规则、稳定，各部分分层流动互不掺混，质点轨迹光滑。
脉线清晰 湍流：流体运动极不规则、极不稳定，伴有高频扰动，各部分激烈掺混，质点轨迹杂乱无章。
决定流动状态的参数是e R 数(Batchlor page255)，e R <<2000 一定是层流，此时粘性力足以保持流动的稳定。
层流：极少有准确解（某些特殊的简单问题，非线性方程得以简化） 近似解法：大e R 数，边界层理论小e R 数，部分或全部忽略惯性力。
8.6 不可压缩粘性流体在无穷长直圆管内流。
由实验知，其璧面传热系数h 与圆管的直径D ，热传导系数k,流体的平均速度U ，密度ρ，粘度系数μ和流体比热c 有关，其中h 具有h/D 的量纲。
试由量纲分析证明 P r ).(R e ,f Nu = 式中khD Nu =叫做努塞尔特（Nusselt ）数，μρUD =Re 是雷诺数，kc μ=Pr 是普朗特数。
解：由题意：,,,,,(][c U k D f h μρ=此式中有n=6个物理量，其中含4=r 个基本量纲，按π定理可简化为2=-r n 个无量纲间的函数关系。
记质量，长度，时间和温度的基本量纲分别为K T L M ,,,写出各量的量纲如下：[]L D =，[][]13)/(--==KMLTLK W k ，[]1-=LT U ，[]3-=ML ρ，11][--=TML μ，[]13--=⎥⎦⎤⎢⎣⎡=KMT D k h ，122][-=KT L c 。
现取D ，k ，U ，ρ为基本量，将其余各量与这些基本量组合成无量纲量。
例如，设]ξγβαρ][][][][U k D h =，列出此式两侧的量纲有：ξγβαβγβξβ3313-++---+--=LKTMKMT显然两侧的幂次应该分别相等：⎪⎪⎩⎪⎪⎨⎧=-++-=--=--=+031331ξγβαβγβξβ解得⎪⎪⎩⎪⎪⎨⎧===-=0011ξγβα，即[]][][1k D h -=，于是khD Nu =构成一个无量纲量。
同理： ),,,,,(][1c U k D h f μρ=，取μ,,,k U D 为基本量，将其余各量与这些基本量组合成无量纲量。
设[]ξγβαμρ][][][][k U D =，列出此式两侧的量纲有：ββξγβαξβ----+++-=KTLMMLr333两侧的幂次应该分别相等：⎪⎪⎩⎪⎪⎨⎧=-=---=-++=+003331βγβξγβαξβ解得⎪⎪⎩⎪⎪⎨⎧====1000ξγβα，8.8截面为半圆形的无限长直管中的不可压缩流体做层流运动，沿管轴方向某一长度l 上的压降为p ∆。
流体力学第八章答案【篇一：流体力学第8、10、11章课后习题】>一、主要内容（一）边界层的基本概念与特征1、基本概念：绕物体流动时物体壁面附近存在一个薄层，其内部存在着很大的速度梯度和漩涡，粘性影响不能忽略，我们把这一薄层称为边界层。
2、基本特征：（1）与物体的长度相比，边界层的厚度很小；（2）边界层内沿边界层厚度方向的速度变化非常急剧，即速度梯度很大；（3）边界层沿着流体流动的方向逐渐增厚；（4）由于边界层很薄，因而可以近似地认为边界层中各截面上压强等于同一截面上边界层外边界上的压强；（5）在边界层内粘性力和惯性力是同一数量级；（6）边界层内流体的流动与管内流动一样，也可以有层流和紊流2种状态。
（二）层流边界层的微分方程（普朗特边界层方程）??v?vy?2v1?p?vy?????vx?x?y??x?y2????p??0?y???v?vy???0?x?y??其边界条件为：在y?0处，vx?vy?0 在y??处，vx?v(x)（三）边界层的厚度从平板表面沿外法线到流速为主流99%的距离，称为边界层的厚度，以?表示。
边界层的厚度?顺流逐渐加厚，因为边界的影响是随着边界的长度逐渐向流区内延伸的。
图8-1 平板边界层的厚度1、位移厚度或排挤厚度?1?1?2、动量损失厚度?2?vx1?(v?v)dy?(1?)dy x??00vv?2?1?v2???vx(v?vx)dy???vxv(1?x)dy vv（四）边界层的动量积分关系式??2???p?vdy?v?vdy?????wdx xx??00?x?x?x对于平板上的层流边界层，在整个边界层内每一点的压强都是相同的，即p?常数。
这样，边界层的动量积分关系式变为?wd?2d?vdy?vvdy?? x?x??00dxdx?二、本章难点（一）平板层流边界层的近似计算根据三个关系式：（1）平板层流边界层的动量积分关系式；（2）层流边界层内的速度分布关系式；（3）切向应力关系式。
流体力学中的流体的黏滞流动在流体力学中，流体的黏滞流动是一个重要的研究课题。
黏滞流动是指当流体通过固体表面时，流体层与固体表面之间存在一种摩擦力，使得流体沿着表面运动。
黏滞流动现象的产生与流体的黏度密切相关。
黏度是指流体抵抗剪切变形的能力。
在流体力学中，黏滞流动可以用牛顿黏度模型来描述。
牛顿黏度模型认为流体的黏度与流速成正比，黏度系数称为黏度。
通常，黏度较大的流体会表现出较大的阻力与摩擦力。
黏滞流动可以分为层流和湍流两种形式。
在层流中，流体沿着固体表面形成的层次运动，运动方向平行，并且速度趋于零。
这种流动形式在细小管道内发生较为常见。
而在湍流中，流体的速度是不规则的，并且会形成涡流。
湍流流动时，流体与固体表面之间会产生混合和扩散。
黏滞流动现象不仅在自然界中普遍存在，也有着广泛的应用。
例如，在工程领域中，黏滞流动的研究对于设计船舶、飞机和汽车等交通工具的外形和动力学性能具有重要意义。
此外，黏滞流动还涉及到石油勘探、化工工艺和环境工程等多个领域。
对于流体黏滞流动的研究，科学家们发展了许多数学模型和实验方法。
其中最重要的模型之一是Navier-Stokes方程，它基于质量守恒、动量守恒和能量守恒原理，揭示了流体的运动规律。
然而，由于Navier-Stokes方程的求解十分困难，目前尚未找到通用的解析解。
因此，科学家们通过数值模拟和实验方法来研究复杂的黏滞流动现象。
实验方法主要包括利用流体动力学实验室进行流体黏滞流动的可视化实验。
通过使用高速摄像机和荧光染料，在实验室中观察和记录流体流动过程。
这些实验可以帮助科学家们研究流体的运动特性，并验证数学模型的准确性。
除了实验方法，数值模拟也成为研究黏滞流动的重要手段。
数值模拟通过使用计算机模拟流体流动，可以模拟各种黏滞流动现象，如层流、湍流、涡流和粘弹性流动等。
通过数值模拟，科学家们可以研究流体黏滞流动的复杂特性，并提供实验不易获得的详细信息。
总的来说，流体的黏滞流动在流体力学中占据着重要地位。
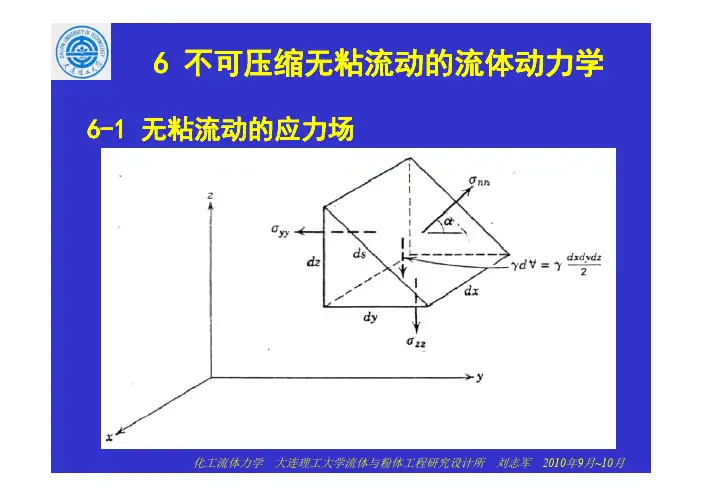
不可压缩无粘流动的流体动力学6 不可压缩无粘流动的流体动力学6无粘流动的应力场1 无粘流动的应力场6 1-1, z方向上微元质量应用牛顿第二定律,微元质量应用牛顿第二定律方程两边同除以dxdydz是微小量y方向的牛顿第二定律可以得出对运动的无粘流体而言，点的正应力各向对运动的无粘流体而言一点的正应力各向相同（即是一个标量），无粘流体中正应力等于热力学压强的负值，即等于热力学压强的负值无摩流动动方程欧方程无摩擦流动的动量方程：欧拉方程2 无摩擦流动的动量方程：欧拉方程6-2N S方程N-S方程在无摩擦流动中不存在剪应力，正应力是热力学压强的负值如果重力是唯一的质量力如果z坐标是垂直方向欧拉方程对于重力是唯的质量力的情况，柱对于重力是唯一的质量力的情况，柱坐标形式的分量方程如下：z轴是垂直向上的，因此，g r gθ，g z g=g=-做刚体运动的流体的欧拉方程3 做刚体运动的流体的欧拉方程6-3流体被加速而在相邻流体层之间没有相对运动，即，流体做没有变形的运动时，就不会产生剪应力。
运用合适的自由体动方程我们确定流体内体运动方程，我们可以确定流体内压强的变化。
的变化直线加速运动的流体绕着垂直轴线做稳定旋转运动的流体欧拉方程可以解决非惯性坐标系中做刚体运动的流体内压强分布的问题，可以得到相同的结果。
流线坐标中的欧拉方程6-44 流线坐标中的欧拉方程流线？定常流动中，流体质点的运动轨迹？流线坐标定常流动中，沿着流线：定常流动中，沿着流线的位移是用于描述运动方程较好的坐标坐标。
在非定常流动中，流线可以给出瞬在非定常流动中流线可以给出瞬时速度场的图形表示时速度场的图形表示。
运动方程可以写成沿着流线的位移坐标sn以及流线的法向位移坐标的表达式在流动方向上（即s方向）对体积为dsdndx的微元流体应用牛顿第二定律，并忽略粘性力β是流线的切线和水平方向的夹角αs 是流体质点沿着流线方向的加速度在流动方向上流体质点的随体加速度在具有垂直方向的z轴坐标系中沿着流线方向标系中，沿着流线方向对于定常流动，忽略质量力时，在流动方向上的欧拉方程速度的减小伴随着压强的增加，成反比关系。
