2014届高三数学一轮复习单元训练：直线与圆

内蒙古大学附中2014版《创新设》高考数学一轮复习单元能力提升训练：直线与圆 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．若2222(0)a b c c +=≠，则直线0ax by c ++=被圆221x y +=所截得的弦长为( ) A ．12B ．1C ．22D ．2【答案】D2．设点(1,0)A ,(2,1)B ,如果直线1ax by +=与线段AB 有一个公共点,那么22a b +( )A ．最小值为15B ．最小值为55C ．最大值为15D ．最大值为55【答案】A3．与直线3450x y -+=关于x 轴对称的直线方程为( )A ．3450x y +-=B ．3450x y ++=C ．3450x y -+-=D ．3450x y -++=【答案】B4．将圆x 2+y 2-2x-4y+1=0平分的直线是( )A ．01=-+y xB ．03=++y xC ．03=+-y xD ．01=+-y x【答案】D5．直线01=-+By Ax 在y 轴上的截距是1-,而且它的倾斜角是直线333=-y x 的倾斜角的二倍,则( ) A ． 1,3==B A B ． 1,3-=-=B A C ． 1,3-==B AD ． 1,3=-=B A【答案】B6．两圆C 1：x 2＋y 2＋2x ＝0，C 2：x 2＋y 2＋4y ＋3＝0的位置关系为( )A ．外离B ． 内含C ．相交D ． 相切【答案】A7．若直线013=--y x 到直线0=-ay x 的角为6π，则实数a 的值等于( ) A ．0B ．3C ．0或3D ．33-8．圆222210x y x y +-++=的圆心到直线10x y -+=的距离是( )A ．12B ．32 C ．22D ．322【答案】D9．如图，直线l 的斜率为( )A ． 33- B ． 3-C ．33 D ． 3【答案】D10．直线mx-y+2m+1=0经过一定点，则该点的坐标是( )A ．（-2，1）B ． (2，1）C ． (1，-2）D ． (1，2）【答案】A 11．过直线y x =上一点P 引圆22670x y x +-+=的切线，则切线长的最小值为( )A ．22 B ．223 C ．210 D ．2【答案】C 12．已知两条直线和互相垂直，则等于( ) A ．2 B ．1C ．0D ．【答案】D第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．①已知点00(,)p x y 在曲线()0f x y ⋅=上，p 也在曲线()g x y ⋅点上，则p 在曲线()()0f x y g x y λ⋅+⋅=上。

北京市2014届高三理科数学一轮复习试题选编20：直线与圆一、选择题1 ．（北京市房山区2013届高三上学期期末考试数学理试题 ）已知圆22:21C x y x +-=，直线:(1)1l y k x =-+，则与C 的位置关系是（ ） A ．一定相离 B ．一定相切C ．相交且一定不过圆心D ．相交且可能过圆心 【答案】C2 ．（2013北京顺义二模数学理科试题及答案）设R ∈n m ,,若直线01:=-+ny mx l 与x 轴相交于点A ,与y 轴相交于点B ,且坐标原点O 到直线l 的距离为3,则AOB ∆的面积S 的最小值为 （ ） A ．21B ．2C ．3D ．4【答案】C ．3 ．（2013北京昌平二模数学理科试题及答案）圆22(2)1x y +-=的圆心到直线3,2x t y t =+⎧⎨=--⎩(t 为参数)的距离为 （ ）A．2B ．1CD．【答案】A ．4 ．（2013北京房山二模数学理科试题及答案）定义运算a b ⎡⎢⎣ c d ⎤⎥⎦x ax cy y bx dy +⎡⎤⎡⎤=⎢⎥⎢⎥+⎣⎦⎣⎦,称x a y b '⎡⎤⎡=⎢⎥⎢'⎣⎦⎣ c d ⎤⎥⎦x y ⎡⎤⎢⎥⎣⎦为将点(),x y 映到点(),x y ''的一次变换.若x y '⎡⎤⎢⎥'⎣⎦=2p ⎡⎢⎣ 1q -⎤⎥⎦x y ⎡⎤⎢⎥⎣⎦把直线y kx =上的各点映到这点本身,而把直线y mx =上的各点映到这点关于原点对称的点.则,,,k m p q 的值依次是 （ ）A ．1,2,3,3k m p q ==-==B ．1,3,3,2k m p q ====-C ．2,3,3,1k m p q =-===D ．2,1,3,3k m p q =-===【答案】B ．5 ．（2013届北京市延庆县一模数学理）已知直线01)1(:1=+++y a ax l ，02:2=++ay x l ，则“2-=a ”是“21l l ⊥”（ ）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A 6 ．（2013届北京丰台区一模理科）动圆C 经过点F(1,0)，并且与直线x=-1相切，若动圆C与直线1y x =+总有公共点，则圆C 的面积（ ）A ．有最大值8πB ．有最小值2πC ．有最小值3πD ．有最小值4π【答案】D 二、填空题7 ．（2013北京海淀二模数学理科试题及答案）在平面直角坐标系中,动点(,)P x y 到两条坐标轴的距离之和等于它到点(1,1)的距离,记点P 的轨迹为曲线W . (I) 给出下列三个结论: ①曲线W 关于原点对称; ②曲线W 关于直线y x =对称;③曲线W 与x 轴非负半轴,y 轴非负半轴围成的封闭图形的面积小于12; 其中,所有正确结论的序号是_____;(Ⅱ)曲线W 上的点到原点距离的最小值为______. 【答案】②③;28 ．（北京市东城区2013届高三上学期期末考试数学理科试题）已知圆C ：22680x y x +-+=，则圆心C 的坐标为 ；若直线y kx =与圆C 相切，且切点在第四象限，则k = ．【答案】(3,0)4-解：圆的标准方程为22(3)1x y -+=，所以圆心坐标为(3,0)，半径为1.要使直线y kx =与圆C 相切，且切点在第四象限，所以有0k <。

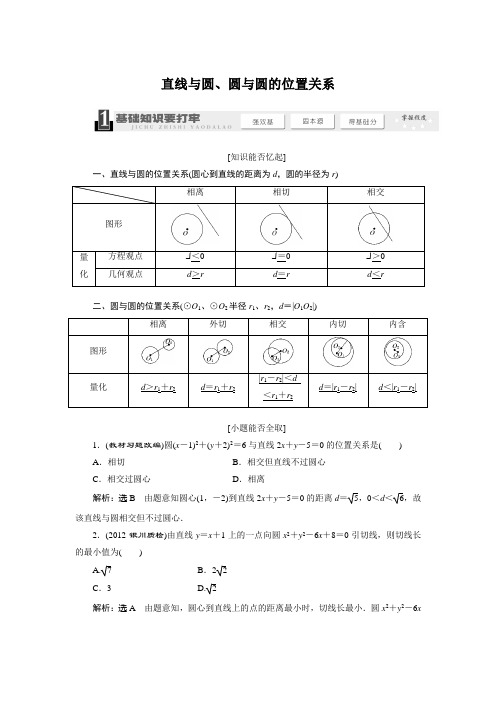
直线与圆、圆与圆的位置关系[知识能否忆起]一、直线与圆的位置关系(圆心到直线的距离为d，圆的半径为r)二、圆与圆的位置关系(⊙O1、⊙O2半径r1、r2，d＝|O1O2|)[小题能否全取]1．(教材习题改编)圆(x－1)2＋(y＋2)2＝6与直线2x＋y－5＝0的位置关系是()A．相切B．相交但直线不过圆心C．相交过圆心D．相离解析：选B由题意知圆心(1，－2)到直线2x＋y－5＝0的距离d＝5，0＜d＜6，故该直线与圆相交但不过圆心．2．(2012·银川质检)由直线y＝x＋1上的一点向圆x2＋y2－6x＋8＝0引切线，则切线长的最小值为()A.7 B．2 2C．3 D. 2解析：选A由题意知，圆心到直线上的点的距离最小时，切线长最小．圆x2＋y2－6x＋8＝0可化为(x－3)2＋y2＝1，则圆心(3,0)到直线y＝x＋1的距离为42＝22，切线长的最小值为(22)2－1＝7.3．直线x －y ＋1＝0与圆x 2＋y 2＝r 2相交于A ，B 两点，且AB 的长为2，则圆的半径为( )A.322B.62C ．1D ．2解析：选B 圆心(0,0)到直线x －y ＋1＝0的距离d ＝12.则r 2＝⎝⎛⎭⎫12|AB |2＋d 2＝32，r ＝62. 4．(教材习题改编)若圆x 2＋y 2＝1与直线y ＝kx ＋2没有公共点，则实数k 的取值范围是________．解析：由题意知21＋k 2＞1，解得－3＜k ＜ 3. 答案：(－3， 3)5．已知两圆C 1：x 2＋y 2－2x ＋10y －24＝0，C 2：x 2＋y 2＋2x ＋2y －8＝0，则两圆公共弦所在的直线方程是____________．解析：两圆相减即得x －2y ＋4＝0. 答案：x －2y ＋4＝01.求圆的弦长问题，注意应用圆的几何性质解题，即用圆心与弦中点连线与弦垂直的性质，可用勾股定理或斜率之积为－1列方程来简化运算．2．对于圆的切线问题，要注意切线斜率不存在的情况．典题导入[例1] (2012·陕西高考) 已知圆C ：x 2＋y 2－4x ＝0，l 是过点P (3,0)的直线，则( ) A ．l 与C 相交 B ．l 与C 相切C ．l 与C 相离D ．以上三个选项均有可能[自主解答] 将点P (3,0)的坐标代入圆的方程，得 32＋02－4×3＝9－12＝－3<0， 所以点P (3,0)在圆内．故过点P 的直线l 定与圆C 相交． [答案] A本例中若直线l 为“x －y ＋4＝0”问题不变． 解：∵圆的方程为(x －2)2＋y 2＝4， ∴圆心(2,0)，r ＝2. 又圆心到直线的距离为d ＝62＝32＞2. ∴l 与C 相离．由题悟法判断直线与圆的位置关系常见的方法(1)几何法：利用圆心到直线的距离d 和圆半径r 的大小关系． (2)代数法：联立直线与圆的方程消元后利用Δ判断．(3)点与圆的位置关系法：若直线恒过定点且定点在圆内可判断直线与圆相交．以题试法1．(2012·哈师大附中月考)已知直线l 过点(－2,0)，当直线l 与圆x 2＋y 2＝2x 有两个交点时，其斜率k 的取值范围是( )A ．(－22，22)B ．(－2，2) C.⎝⎛⎭⎫－24，24D.⎝⎛⎭⎫－18，18 解析：选C 易知圆心坐标是(1,0)，圆的半径是1，直线l 的方程是y ＝k (x ＋2)，即kx －y ＋2k ＝0，根据点到直线的距离公式得|k ＋2k |k 2＋1＜1，即k 2＜18，解得－24＜k ＜24.典题导入[例2] (1)(2012·广东高考)在平面直角坐标系xOy 中，直线3x ＋4y －5＝0与圆x 2＋y 2＝4相交于A 、B 两点，则弦AB 的长等于( )A ．33B ．2 3 C. 3D ．1(2)(2012·天津高考)设m ，n ∈R ，若直线(m ＋1)x ＋(n ＋1)y －2＝0与圆(x －1)2＋(y －1)2＝1相切，则m ＋n 的取值范围是( )A ．[1－3，1＋ 3 ]B ．(－∞，1－ 3 ]∪[1＋3，＋∞)C ．[2－22，2＋2 2 ]D ．(－∞，2－2 2 ]∪[2＋22，＋∞)[自主解答] (1)圆x 2＋y 2＝4的圆心(0,0)，半径为2，则圆心到直线3x ＋4y －5＝0的距离d ＝532＋42＝1. 故|AB |＝2r 2－d 2＝24－1＝2 3.(2)圆心(1,1)到直线(m ＋1)x ＋(n ＋1)y －2＝0的距离为|m ＋n |(m ＋1)2＋(n ＋1)2＝1，所以m ＋n＋1＝mn ≤14(m ＋n )2，整理得[(m ＋n )－2]2－8≥0，解得m ＋n ≥2＋22或m ＋n ≤2－2 2.[答案] (1)B (2)D由题悟法1．圆的弦长的常用求法：(1)几何法：设圆的半径为r ，弦心距为d ，弦长为l ，则⎝⎛⎭⎫l 22＝r 2－d 2. (2)代数方法：运用韦达定理及弦长公式： |AB |＝1＋k 2|x 1－x 2|＝(1＋k 2)[(x 1＋x 2)2－4x 1x 2]. [注意] 常用几何法研究圆的弦的有关问题．2．求过一点的圆的切线方程时，首先要判断此点与圆的位置关系，若点在圆内，无解；若点在圆上，有一解；若点在圆外，有两解．以题试法2．(2012·杭州模拟)直线y ＝kx ＋3与圆(x －2)2＋(y －3)2＝4相交于M ，N 两点，若|MN |≥23，则k 的取值范围是( )A.⎣⎡⎦⎤－34，0B.⎣⎡⎦⎤－33，33 C ．[－3， 3]D.⎣⎡⎦⎤－23，0解析：选B 如图，设圆心C (2,3)到直线y ＝kx ＋3的距离为d ，若|MN |≥23，则d 2＝r 2－⎝⎛⎭⎫12|MN |2≤4－3＝1，即|2k |21＋k2≤1，解得－33≤k ≤ 33.典题导入[例3] (1)(2012·山东高考)圆(x ＋2)2＋y 2＝4与圆(x －2)2＋(y －1)2＝9的位置关系为( )A ．内切B ．相交C ．外切D ．相离(2)设两圆C 1、C 2都和两坐标轴相切，且都过点(4,1)，则两圆心的距离|C 1C 2|＝________. [自主解答] (1)两圆圆心分别为(－2,0)，(2,1)，半径分别为2和3，圆心距d ＝42＋1＝17.∵3－2＜d ＜3＋2，∴两圆相交．(2)由题意可设两圆的方程为(x －r i )2＋(y －r i )2＝r 2i ，r i ＞0，i ＝1,2.由两圆都过点(4,1)得(4－r i )2＋(1－r i )2＝r 2i ，整理得r 2i －10r i ＋17＝0，此方程的两根即为两圆的半径r 1，r 2，所以r 1r 2＝17，r 1＋r 2＝10，则|C 1C 2|＝(r 1－r 2)2＋(r 1－r 2)2＝2×(r 1＋r 2)2－4r 1r 2＝ 2×100－68＝8.[答案] (1)B (2)8由题悟法两圆位置关系的判断常用几何法，即利用两圆圆心之间的距离与两圆半径之间的关系，一般不采用代数法．若两圆相交，则两圆公共弦所在直线的方程可由两圆的方程作差得到．以题试法3．(2012·青岛二中月考)若⊙O ：x 2＋y 2＝5与⊙O 1：(x －m )2＋y 2＝20(m ∈R )相交于A 、B 两点，且两圆在点A 处的切线互相垂直，则线段AB 的长是________．解析：依题意得|OO 1|＝5＋20＝5，且△OO 1A 是直角三角形，S △O O 1A ＝12·|AB |2·|OO 1|＝12·|OA |·|AO 1|，因此|AB |＝2·|OA |·|AO 1||OO 1|＝2×5×255＝4. 答案：4一、选择题1．(2012·人大附中月考)设m ＞0，则直线2(x ＋y )＋1＋m ＝0与圆x 2＋y 2＝m 的位置关系为( )A ．相切B ．相交C ．相切或相离D ．相交或相切解析：选C 圆心到直线l 的距离为d ＝1＋m 2，圆半径为m .因为d －r ＝1＋m 2－m ＝12(m －2m ＋1)＝12(m －1)2≥0，所以直线与圆的位置关系是相切或相离．2．(2012·福建高考)直线x ＋3y －2＝0与圆x 2＋y 2＝4相交于A ，B 两点，则弦AB 的长度等于( )A ．2 5B ．2 3 C. 3D ．1解析：选B 因为圆心(0,0)到直线x ＋3y －2＝0的距离为1，所以AB ＝24－1＝2 3. 3．(2012·安徽高考)若直线x －y ＋1＝0与圆(x －a )2＋y 2＝2有公共点，则实数a 的取值范围是( )A ．[－3，－1]B ．[－1,3]C ．[－3,1]D ．(－∞，－3]∪[1，＋∞)解析：选C 欲使直线x －y ＋1＝0与圆(x －a )2＋y 2＝2有公共点，只需使圆心到直线的距离小于等于圆的半径2即可，即|a －0＋1|12＋(－1)2≤2，化简得|a ＋1|≤2，解得－3≤a ≤1.4．过圆x 2＋y 2＝1上一点作圆的切线与x 轴，y 轴的正半轴交于A ，B 两点，则|AB |的最小值为( )A. 2B. 3 C ．2D ．3解析：选C 设圆上的点为(x 0，y 0)，其中x 0>0，y 0>0，则切线方程为x 0x ＋y 0y ＝1.分别令x ＝0，y ＝0得A ⎝⎛⎭⎫1x 0，0，B ⎝⎛⎭⎫0，1y 0，则|AB |＝ ⎝⎛⎭⎫1x 02＋⎝⎛⎭⎫1y 02＝1x 0y 0≥1x 20＋y 202＝2.当且仅当x 0＝y 0时，等号成立．5．(2013·兰州模拟)若圆x 2＋y 2＝r 2(r ＞0)上仅有4个点到直线x －y －2＝0的距离为1，则实数r 的取值范围为( )A ．(2＋1，＋∞)B ．(2－1, 2＋1)C ．(0, 2－1)D ．(0, 2＋1)解析：选A 计算得圆心到直线l 的距离为22＝ 2＞1，如图．直线l ：x －y －2＝0与圆相交，l 1，l 2与l 平行，且与直线l 的距离为1，故可以看出，圆的半径应该大于圆心到直线l 2的距离 2＋1.6．(2013·临沂模拟)已知点P (x ，y )是直线kx ＋y ＋4＝0(k ＞0)上一动点，P A ，PB 是圆C ：x 2＋y 2－2y ＝0的两条切线，A ，B 是切点，若四边形P ACB 的最小面积是2，则k 的值为( )A. 2B.212C ．2 2D ．2解析：选D 圆心C (0,1)到l 的距离d ＝5k 2＋1， 所以四边形面积的最小值为2×⎝⎛⎭⎫12×1×d 2－1＝2， 解得k 2＝4，即k ＝±2. 又k ＞0，即k ＝2.7．(2012·朝阳高三期末)设直线x －my －1＝0与圆(x －1)2＋(y －2)2＝4相交于A 、B 两点，且弦AB 的长为23，则实数m 的值是________．解析：由题意得，圆心(1,2)到直线x －my －1＝0的距离d ＝4－3＝1，即|1－2m －1|1＋m 2＝1，解得m ＝±33.答案：±338．(2012·东北三校联考)若a ，b ，c 是直角三角形ABC 三边的长(c 为斜边)，则圆C ：x 2＋y 2＝4被直线l ：ax ＋by ＋c ＝0所截得的弦长为________．解析：由题意可知圆C ：x 2＋y 2＝4被直线l ：ax ＋by ＋c ＝0所截得的弦长为 2 4－⎝ ⎛⎭⎪⎫c a 2＋b 22，由于a 2＋b 2＝c 2，所以所求弦长为2 3. 答案：2 39．(2012·江西高考)过直线x ＋y －22＝0上点P 作圆x 2＋y 2＝1的两条切线，若两条切线的夹角是60°，则点P 的坐标是________．解析：∵点P 在直线x ＋y －22＝0上，∴可设点P (x 0，－x 0＋22)，且其中一个切点为M .∵两条切线的夹角为60°，∴∠OPM ＝30°.故在Rt △OPM 中，有OP ＝2OM ＝2.由两点间的距离公式得OP ＝x 20＋(－x 0＋22)2＝2，解得x 0＝ 2.故点P 的坐标是( 2， 2)．答案：( 2， 2)10．(2012·福州调研)已知⊙M ：x 2＋(y －2)2＝1，Q 是x 轴上的动点，QA ，QB 分别切⊙M 于A ，B 两点．(1)若|AB |＝423，求|MQ |及直线MQ 的方程； (2)求证：直线AB 恒过定点．解：(1)设直线MQ 交AB 于点P ，则|AP |＝223，又|AM |＝1，AP ⊥MQ ，AM ⊥AQ ，得|MP |＝12－89＝13，又∵|MQ |＝|MA |2|MP |，∴|MQ |＝3.设Q (x,0)，而点M (0,2)，由x 2＋22＝3，得x ＝±5， 则Q 点的坐标为(5，0)或(－5，0)．从而直线MQ 的方程为2x ＋5y －25＝0或2x －5y ＋25＝0.(2)证明：设点Q (q,0)，由几何性质，可知A ，B 两点在以QM 为直径的圆上，此圆的方程为x (x －q )＋y (y －2)＝0，而线段AB 是此圆与已知圆的公共弦，相减可得AB 的方程为qx －2y ＋3＝0，所以直线AB 恒过定点⎝⎛⎭⎫0，32. 11．已知以点C ⎝⎛⎭⎫t ，2t (t ∈R ，t ≠0)为圆心的圆与x 轴交于点O 、A ，与y 轴交于点O 、B ，其中O 为原点．(1)求证：△AOB 的面积为定值；(2)设直线2x ＋y －4＝0与圆C 交于点M 、N ，若|OM |＝|ON |，求圆C 的方程． 解：(1)证明：由题设知，圆C 的方程为 (x －t )2＋⎝⎛⎭⎫y －2t 2＝t 2＋4t 2， 化简得x 2－2tx ＋y 2－4t y ＝0，当y ＝0时，x ＝0或2t ，则A (2t,0)； 当x ＝0时，y ＝0或4t ，则B ⎝⎛⎭⎫0，4t ， 所以S △AOB ＝12|OA |·|OB |＝12|2t |·⎪⎪⎪⎪4t ＝4为定值． (2)∵|OM |＝|ON |，则原点O 在MN 的中垂线上，设MN 的中点为H ，则CH ⊥MN ，∴C 、H 、O 三点共线，则直线OC 的斜率 k ＝2t t ＝2t 2＝12，∴t ＝2或t ＝－2.∴圆心为C (2,1)或C (－2，－1)，∴圆C 的方程为(x －2)2＋(y －1)2＝5或(x ＋2)2＋(y ＋1)2＝5，由于当圆方程为(x ＋2)2＋(y ＋1)2＝5时，直线2x ＋y －4＝0到圆心的距离d ＞r ，此时不满足直线与圆相交，故舍去，∴圆C 的方程为(x －2)2＋(y －1)2＝5.12．在平面直角坐标系xOy 中，已知圆x 2＋y 2－12x ＋32＝0的圆心为Q ，过点P (0,2)，且斜率为k 的直线与圆Q 相交于不同的两点A 、B .(1)求k 的取值范围；(2)是否存在常数k ，使得向量OA ＋OB 与PQ共线？如果存在，求k 值；如果不存在，请说明理由．解：(1)圆的方程可写成(x －6)2＋y 2＝4，所以圆心为Q (6,0)．过P (0,2)且斜率为k 的直线方程为y ＝kx ＋2，代入圆的方程得x 2＋(kx ＋2)2－12x ＋32＝0，整理得(1＋k 2)x 2＋4(k －3)x ＋36＝0.①直线与圆交于两个不同的点A 、B 等价于Δ＝[4(k －3)]2－4×36(1＋k 2)＝42(－8k 2－6k )>0，解得－34<k <0，即k 的取值范围为⎝⎛⎭⎫－34，0. (2)设A (x 1，y 1)、B (x 2，y 2)则OA ＋OB＝(x 1＋x 2，y 1＋y 2)，由方程①得x 1＋x 2＝－4(k －3)1＋k 2.②又y 1＋y 2＝k (x 1＋x 2)＋4.③因P (0,2)、Q (6,0)，PQ＝(6，－2)，所以OA ＋OB 与PQ共线等价于－2(x 1＋x 2)＝6(y 1＋y 2)，将②③代入上式，解得k ＝－34. 而由(1)知k ∈⎝⎛⎭⎫－34，0，故没有符合题意的常数k.1．已知两圆x 2＋y 2－10x －10y ＝0，x 2＋y 2＋6x －2y －40＝0，则它们的公共弦所在直线的方程为________________；公共弦长为________．解析：由两圆的方程x 2＋y 2－10x －10y ＝0，x 2＋y 2＋6x －2y －40＝0，相减并整理得公共弦所在直线的方程为2x ＋y －5＝0.圆心(5,5)到直线2x ＋y －5＝0的距离为105＝25，弦长的一半为50－20＝30，得公共弦长为230.答案：2x ＋y －5＝0 2302．(2012·上海模拟)已知圆的方程为x 2＋y 2－6x －8y ＝0，a 1，a 2，…，a 11是该圆过点(3,5)的11条弦的长，若数列a 1，a 2，…，a 11成等差数列，则该等差数列公差的最大值是________．解析：容易判断，点(3,5)在圆内部，过圆内一点最长的弦是直径，过该点与直径垂直的弦最短，因此，过(3,5)的弦中，最长为10，最短为46，故公差最大为10－4610＝5－265.答案：5－2653.(2012·江西六校联考)已知抛物线C ：y 2＝2px (p ＞0)的准线为l ，焦点为F ，圆M 的圆心在x 轴的正半轴上，圆M 与y 轴相切，过原点O 作倾斜角为π3的直线n ，交直线l 于点A ，交圆M 于不同的两点O 、B ，且|AO |＝|BO |＝2.(1)求圆M 和抛物线C 的方程；(2)若P 为抛物线C 上的动点，求PM ,·PF,的最小值；(3)过直线l 上的动点Q 向圆M 作切线，切点分别为S 、T ，求证：直线ST 恒过一个定点，并求该定点的坐标．解：(1)易得B (1，3)，A (－1，－3)，设圆M 的方程为(x －a )2＋y 2＝a 2(a ＞0)， 将点B (1，3)代入圆M 的方程得a ＝2，所以圆M 的方程为(x －2)2＋y 2＝4，因为点A (－1，－3)在准线l 上，所以p2＝1，p ＝2，所以抛物线C 的方程为y 2＝4x .(2)由(1)得，M (2,0)，F (1,0)，设点P (x ，y )，则PM ,＝(2－x ，－y )，PF,＝(1－x ，－y )，又点P 在抛物线y 2＝4x 上，所以PM ,·PF ,＝(2－x )(1－x )＋y 2＝x 2－3x ＋2＋4x ＝x 2＋x＋2，因为x ≥0，所以PM ,·PF ,≥2，即PM ,·PF,的最小值为2.(3)证明：设点Q (－1，m )，则|QS |＝|QT |＝m 2＋5，以Q 为圆心，m 2＋5为半径的圆的方程为(x ＋1)2＋(y －m )2＝m 2＋5，即x 2＋y 2＋2x －2my －4＝0，①又圆M 的方程为(x －2)2＋y 2＝4，即x 2＋y 2－4x ＝0，② 由①②两式相减即得直线ST 的方程3x －my －2＝0， 显然直线ST 恒过定点⎝⎛⎭⎫23，0.1．两个圆：C 1：x 2＋y 2＋2x ＋2y －2＝0与C 2：x 2＋y 2－4x －2y ＋1＝0的公切线有且仅有( )A ．1条B ．2条C ．3条D ．4条解析：选B 由题知C 1：(x ＋1)2＋(y ＋1)2＝4，则圆心C 1(－1，－1)，C 2：(x －2)2＋(y －1)2＝4，圆心C 2(2,1)，两圆半径均为2，又|C 1C 2|＝(2＋1)2＋(1＋1)2＝13＜4，则两圆相交⇒只有两条外公切线．2．(2012·江苏高考)在平面直角坐标系xOy 中，圆C 的方程为x 2＋y 2－8x ＋15＝0，若直线y ＝kx －2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则k 的最大值是________．解析：设圆心C (4,0)到直线y ＝kx －2的距离为d ，则d ＝|4k －2|k 2＋1，由题意知，问题转化为d ≤2，即d ＝|4k －2|k 2＋1≤2，得0≤k ≤43，所以k max ＝43. 答案：433．过点(－1，－2)的直线l 被圆x 2＋y 2－2x －2y ＋1＝0截得的弦长为 2，则直线l 的斜率为________．解析：将圆的方程化成标准方程为(x －1)2＋(y －1)2＝1，其圆心为(1,1)，半径r ＝1.由弦长为2得弦心距为22.设直线方程为y ＋2＝k (x ＋1)，即kx －y ＋k －2＝0，则|2k －3|k 2＋1＝22，化简得7k 2－24k ＋17＝0，得k ＝1或k ＝177. 答案：1或1774．圆O 1的方程为x 2＋(y ＋1)2＝4，圆O 2的圆心为O 2(2,1)．(1)若圆O 2与圆O 1外切，求圆O 2的方程；(2)若圆O 2与圆O 1交于A 、B 两点，且|AB |＝22，求圆O 2的方程．解：(1)设圆O 2的半径为r 2，∵两圆外切，∴|O 1O 2|＝r 1＋r 2，r 2＝|O 1O 2|－r 1＝2(2－1)，故圆O 2的方程是(x －2)2＋(y －1)2＝4(2－1)2.(2)设圆O 2的方程为(x －2)2＋(y －1)2＝r 22，又圆O 1的方程为x 2＋(y ＋1)2＝4，此两圆的方程相减，即得两圆公共弦AB 所在直线的方程：4x ＋4y ＋r 22－8＝0.因为圆心O 1(0，－1)到直线AB 的距离为|r 22－12|42＝ 4－⎝⎛⎭⎫2222＝2，解得r22＝4或r22＝20.故圆O2的方程为(x－2)2＋(y－1)2＝4或(x－2)2＋(y－1)2＝20.。

2014届高三数学理科第一轮复习单元过关( 12) 考查：直线与圆一、选择题：(本大题共8小题，每小题5分，共40分,在每小题给出的四个选项中，有且只有一项是符合题目要求的.)1． 若直线l 与直线1y =,7x =分别交于点P 、Q ,且线段P Q 的中点坐标为(1,1)-,则直线l 的斜率为( ) A.13 B.13- C.32- D.23 2．若直线1:60l x ay ++=与2:(2)320l a x y a -++=平行，则1l 与2l 间的距离为( )B.33．如果0A C ⋅<,且0B C ⋅<,那么直线0Ax By C ++=不经过( ). A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限4．直线20ax y a -+=与圆229x y +=的位置关系是( )A ．相离B ．相切C ．相交D ．不确定5. 若函数8y ax =+与12y x b =-+的图象关于直线y x =对称，则a b +=( )A.1B.2D.46．直线1l 的斜率为2，12//l l ，直线2l 过点(1,1)-)且与y 轴交于点P ,则P 点坐标为( )A ．(3,0)B ．(3,0)-C ．(0,3)-D ．(0,3)7. 已知直线1l 与圆2220x y y ++=相切,且与直线2:3460l x y +-=平行,则直线l 1的方程是( )A ．3410x y +-=B ．3410x y ++=或3490x y +-=C ．3490x y ++=D ．3410x y +-=或3490x y ++=8．若圆222()()1x a y b b -+-=+始终平分圆22(1)(1)4x y +++=的周长，则a b 、 满足的关系是( )A ．22230a a b ++-=B ．222250a b a b ++++=C ．22250a a b +++=D ．22250a a b --+=二、填空题: (本大题共6小题,每小题5分,共30分,把答案填在答题卷中．．．．相应横线上)9. 圆心在原点且与直线24x y +=相切的圆的方程是 .10.点(4,2)P -与圆224x y +=上任一点连线的中点的轨迹方程是___________.11．在平面直角坐标系xOy 中，已知圆224x y +=上有且只有四个点到直线1250x y c -+=的距离为1，则实数c 的取值范围是________.12.已知点(1,3),(2,1)A B --,若直线:(2)1l y k x =-+与线段AB 相交,则k 的取值范围是________.13.圆心在曲线3(0)y x x=>上，且与直线3430x y ++=相切的面积最小的圆的方程为14．已知实数x y 、满足250x y ++=,的最小值为 .二、填空题(每小题5分,共30分)9.____________________. 10.___________________. 11. ____________________.12.___________________. 13. ___________________. 14.____________________.三、解答题：本大题共4小题，解答应写出文字说明，证明过程或演算步骤15．已知直线l 与两坐标轴围成的三角形的面积为3，且经过点(3,4)A -,求直线l 的方程.16．不同两点P 、Q 的坐标分别为(,),(3,3)a b b a --，求:()Ⅰ线段P Q 的垂直平分线l 的方程;()Ⅱ圆22(2)(3)1x y -+-=关于直线l 对称的圆的方程.17．已知圆22:2440C x y x y +-+-=,是否存在斜率为1的直线l ,使以l 被圆截得的弦AB 为直径的圆过原点？若存在,求出直线l 的方程;若不存在,说明理由.18.在直角坐标系xOy 中，以O为圆心的圆与直线40x +=相切. ()Ⅰ求圆O 的方程;()Ⅱ圆O 与x 轴相交于A B 、两点，圆内的动点P 使PA PO PB、、|成等比数列,求PA PB ⋅的取值范围.2014届高三数学理科第一轮复习单元过关( 12)参考答案1解析：选B.由直线l 与直线y ＝1，x ＝7分别交于点P 、Q ，可设P (x 1,1)，Q (7，y 1)，再由线段PQ 的中点坐标为(1，－1)，可解得：x 1＝－5，y 1＝－3.即直线l 上有两点P (－5,1)，Q (7，－3)，代入斜率公式可解得直线l 的斜率为k ＝1＋3－5－7＝－13.故选B.2 [解析]由l 1∥l 2知3＝a(a －2)且2a ≠6(a －2)，2a 2≠18，求得a ＝－1，l 1：x －y ＋6＝0，l 2：x －y ＋23＝0，两条平行直线l 1与l 2间的距离为d ＝|6－23|12＋(－1)2＝823.故选B. 3．C 解析：由A·C ＜0及B·C ＜0，可知A ≠0，B ≠0，又直线Ax ＋By ＋C ＝0过⎝⎛⎭⎫－CA ，0，⎝⎛⎭⎫0，－CB ，且－C A ＞0，－C B＞0，∴直线不过第三象限．4[解析]直线ax －y ＋2a ＝0⇒a(x ＋2)－y ＝0，即直线恒过点(－2,0)，∵点(－2,0)在圆内，所以直线与圆相交，故选C.5解析：直线y ＝ax ＋8关于y ＝x 对称的直线方程为x ＝ay ＋8，所以x ＝ay ＋8与y ＝－12x＋b 为同一直线，故得⎩⎪⎨⎪⎧a ＝－2b ＝4，所以a ＋b ＝2故选B6.解析：∵点P 在y 轴上，∴设P(0，y)，又∵kl 1＝2，l 1∥l 2，∴kl 2＝y －10－(－1)＝y －1＝2，∴y ＝3，∴P(0,3)．答案：D7.D 解析：设直线l 1的方程为3x ＋4y ＋m ＝0.∵直线l 1与圆x 2＋y 2＋2y ＝0相切，∴|－4＋m|32＋42＝1.∴|m －4|＝5.∴m ＝－1或m ＝9.∴直线l 1的方程为3x ＋4y －1＝0或3x ＋4y ＋9＝0.8.解析 即两圆的公共弦必过(x ＋1)2＋(y ＋1)2＝4的圆心，两圆相减得相交弦的方程为－2(a ＋1)x －2(b ＋1)y ＋a 2＋1＝0,将圆心坐标(－1,－1)代入可得a 2＋2a ＋2b ＋5＝0.答案C9解析：由题意，半径R ＝41＋22＝45，所以圆的方程为x 2＋y 2＝165，故填x 2＋y 2＝165.10解析：设圆上任一点为Q(s ，t)，PQ 的中点为A(x ，y)，则⎩⎨⎧x ＝4＋s 2y ＝－2＋t2，解得⎩⎪⎨⎪⎧s ＝2x －4t ＝2y ＋2，将其代入圆的方程，得(2x －4)2＋(2y ＋2)2＝4，整理得(x －2)2＋(y ＋1)2＝1 11.解析 (数形结合法)由已知直线l 恒过定点P(2,1)，如右图．若l 与线AB 相交，则k PA ≤k ≤k PB ，∵k PA ＝－2，k PB ＝12，∴－2≤k ≤1212.[解析] 本题考查了直线与圆的位置关系，利用数形结合可解决此题，属中档题．要使圆x 2＋y 2＝4上有且只有四个点到直线12x －5y ＋c ＝0的距离为1，只需满足圆心到直线的距离小于1即可．即|c|122＋52<1，解|c|<13，∴－13<c<13.13.解析：设圆心(a ，3a )(a>0),则圆心到直线的距离d ＝|3a ＋12a ＋3|5，而d ≥15(23a ·12a ＋3)＝3,当且仅当3a ＝12a ，即a ＝2时，取“＝”，此时圆心为(2，32)，半径为3，圆的方程为(x －2)2＋(y －32)2＝9.14.解析：x 2＋y 2表示点(x ，y)到原点的距离．根据数形结合得x 2＋y 2的最小值为原点到直线2x ＋y ＋5＝0的距离，即d ＝55＝ 5.15.解析：设直线l 的方程是y ＝k(x ＋3)＋4，它在x 轴，y 轴上的截距分别是－4k－3,3k ＋4，由已知，得(3k ＋4)(4k ＋3)＝±6，解得k 1＝－23或k 2＝－83.故直线l 的方程为2x ＋3y －6＝0或8x ＋3y ＋12＝0. 16.【解析】（1）∵313P a bk b a--==--Q ，∴11l P k k =-=-Q ， ∵P Q 的中点坐标为33(,)22，直线l 的方程为3x y +=．（2）设所求圆的圆心为(,)a b ，则31223322l b k a a b -⎧⨯=-⎪⎪-⎨++⎪+=⎪⎩，解得01a b =⎧⎨=⎩， ∴所求圆的圆方程为22(1)1x y +-=．17解析 假设存在斜率为1的直线l ，满足题意，则OA ⊥OB.设直线l 的方程是y ＝x ＋b ，其与圆C 的交点A ，B 的坐标分别为A(x 1，y 1)，B(x 2，y 2)则y 1x 1·y 2x 2＝－1，即x 1x 2＋y 1y 2＝0①由⎩⎪⎨⎪⎧y ＝x ＋b ，x 2＋y 2－2x ＋4y －4＝0消去y 得： 2x 2＋2(b ＋1)x ＋b 2＋4b －4＝0， ∴x 1＋x 2＝－(b ＋1)，x 1x 2＝12(b 2＋4b －4)，②y 1y 2＝(x 1＋b)(x 2＋b)＝x 1x 2＋b(x 1＋x 2)＋b 2＝12(b 2＋4b －4)－b 2－b ＋b 2＝12(b 2＋2b －4)．③把②③式代入①式，得b 2＋3b －4＝0，解得b ＝1或b ＝－4，且b ＝1或b ＝－4都使得Δ＝4(b ＋1)2－8(b 2＋4b －4)＞0成立．故存在直线l 满足题意，其方程为y ＝x ＋1或y ＝x －4.法二:可设直线l :0x y c -+=,经过A B 、的圆:22:244()0C x y x y x y c λ+-+-+-+=分析18.解析：(1)依题设，圆O 的半径r 等于原点O 到直线x －3y ＋4＝0的距离，即r ＝41＋3＝2.所以圆O 的方程为x 2＋y 2＝4.(2)不妨设A(x 1,0)，B(x 2,0)，x 1<x 2.由x 2＝4即得A(－2,0)，B(2,0)．设P(x ，y)，由|PA →|，|PO →|，|PB →|成等比数列，得(x ＋2)2＋y 2·(x －2)2＋y 2＝x 2＋y 2，即x 2－y 2＝2.PA →·PB →＝(－2－x ，－y)· (2－x ，－y)＝x 2－4＋y 2＝2(y 2－1)．由于点P 在圆O 内，故⎩⎪⎨⎪⎧x 2＋y 2<4x 2－y 2＝2，由此得y 2<1.所以PA →·PB →的取值范围为[－2,0)．。

东南大学附中2014三维设计高考数学一轮单元复习精品练习：直线与圆本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．由圆x 2+y 2=4外一动点P 向该圆引两条切线PA 和PB ，若保持∠APB=60°，则点P 的轨迹方程为（ ）A ． x 2+y 2=8B ． x 2+y 2=16C ． x 2+y 2=32D ． x 2+y 2=64 【答案】B2．直线0Ax By +=，若从0,1,2,3,5,7这六个数字中每次取两个不同的数作为A,B 的值，则表示成不同直线的条数是( ) A ．2 B ．12C ．22D ．25【答案】C 3．由直线1y x =+上的一点向圆引切线，则切线长的最小值为( )A ．1BC ．D ．3【答案】B4．若圆C 的半径为1，圆心在第一象限，且与直线034=-y x 和x 轴都相切，则该圆的标准方程是( )A ． 1)37()3(22=-+-y x B ．1)1()2(22=-+-y x C ． 1)3()1(22=-+-y x D ．1)1()23(22=-+-y x 【答案】B5．下列四个命题中，正确命题有( )①直线方程的一般式为Ax + By + C = 0 ②k 1·k 2 = –1为两直线垂直的充要条件③k 1 = k 2为两直线平行的必要非充分条件 ④l ：A 1x + B 1y + C 1 = 0和l 2：A 2x + B 2y + C 2 = 0，（B 1≠0，B 2≠0，A 1A 2 + B 1B 2≠0），则直线l 1到l 2的角θ的正切值为21211221tan B B A A B A B A +-=θA ．0个B ．1个C ．2个D ．3个【答案】B6．圆22:420C x y x y +-+=关于直线1y x =+对称的圆的方程是( )A ． 22(1)(2)5x y ++-= B ． 22(4)(1)5x y ++-= C ． 22(2)(3)5x y ++-= D ． 22(2)(3)5x y -++=【答案】B7．若圆221x y +=与直线340x y m -+=相切，则m 的值等于( )A ．5B ．5-C ．5或5-D ．15或15- 【答案】C 8．已知两点()()7,4,5,6AB --，则线段AB 的垂直平分线的方程为( )A ．56110x y ++=B ．6510x y --=C ．56110x y +-=D ．6510x y -+=【答案】B 9．直线3x +2y= 1的倾斜角是( ) A ．arctan 23B ．arctan ( –23) C ．π + arctan 23D ．π + arctan ( –23) 【答案】D10．设圆222)5()3(r y x =+++上有且只有两点到直线234=-y x 的距离等于1，则圆的半径r 的取值范围为( ) A ．561<<r B ．54>r C ．5654<<r D ．1>r【答案】C11．圆122=+y x 上的点到直线02543=-+y x 的距离的最小值为( )A ．6B ．2C ．3D ．4【答案】D12．在平面直角坐标系xOy 中，直线3x+4y-5=0与圆2x +2y =4相交于A 、B 两点，则弦AB 的长等于( )A ．B ．C ．D ． 1【答案】C第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．若三条直线1l ：032=-+y x ，2l ：023=+-y x 和3l ：0=+y ax 不能构成三角形，则a 的值为【答案】13a =-或2a =或3a =-14．在平面直角坐标系中，不等式组⎪⎩⎪⎨⎧≤≥+-≥+a x y x y x 040，（a 为常数）表示的平面区域的面积是9，那么a 的值为____________. 【答案】115．若方程02222=++-y x my x 表示两条直线，则m 的取值是 ． 【答案】116．过原点O 作圆x 2+y 2-－6x －8y ＋20=0的两条切线，设切点分别为P 、Q ，则线段PQ 的长为 。

南京大学附中2014届高三数学一轮复习单元训练：直线与圆本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．若直线220(0,0)ax by a b -+=>>经过圆222410x y x y ++-+=的圆心，则ba 11+的最小值是( ) A ．41 B ．4C ．21 D ．2【答案】B2．点（2，1）到直线3x -4y + 5=0的距离是( )A ．57B ．75C ．257D ．725【答案】A3．已知圆x 2+y 2=r 2在曲线|x|+|y|=4的内部，则半径r 的范围是( )A ．0<r<22B ．0<r<2C ． 0<r<2D ．0<r<4【答案】A4．对任意实数m ,直线(1)260m x m y -++=必经过的定点是( )A ．(1,0)B ．(0,3)-C ．(6,3)-D ． 63(,)1m m-- 【答案】C5．圆06422=+-+y x y x 和圆0622=-+x y x 交于A 、B 两点，则AB 的垂直平分线的方程是( )A ．x+y+3=0B ．2x-y-5=0C ． 3x-y-9=0D ．4x-3y+7=0【答案】C6．点(a,b)关于直线x+y=0对称的点是( )A ．(－a,－b)B ．(a,－b)C ．(b,a)D ．(－b,－a)【答案】D7．不等边ABC ∆的三个内角所对边分别是a ，b ，c ，且lgsin,lgsin ,lgsin A B C 成等差数列，则直线2sin sin x A y A a +=与直线2sin sin x B y C c +=的位置关系是( ) A ．平行 B ．垂直C ．重合D ．相交但不垂直【答案】C8．半径分别为1和2的两圆外切,作半径为3的圆与这两圆均相切,则一共可作( )个A ．3B ．4C ．5D ．6【答案】C 9．圆心为，且过点的圆的方程为( )A ．B ．C ．D ．【答案】A10．已知直线l 的倾斜角为300，则直线的斜率k 值为( )A ．33 B ．21 C ．3D ．23 【答案】A11．已知直线过定点（－1，1），则“直线的斜率为0”是“直线与圆122=+y x 相切”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A12．过点(1,0)M 和(0,1)N 的直线方程是( )A ．10x y +-=B ．10x y -+=C ．10x y --=D ．10x y ++=【答案】A第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．过点P(2,3)且在两轴上的截距相等的直线方程是____________. 【答案】32050x y x y -=+-=与14．若直线)0,0(>>=+b a ab by ax 与圆122=+y x 相切，则ab 的最小值是 . 【答案】215．已知圆224x y +=与圆22260x y ay ++-=（a>0）的公共弦的长为23，则=a 。

北京体育大学附中2014版《创新设计》高考数学一轮复习单元突破：直线与圆本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．满分150分．考试时间120分钟．第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．平行直线x －y+1=0和x －y －3=0之间的距离是( )A ．22B ．2C ．4D ．2【答案】A2．直线30x y m -+=与圆22220x y x +--=相切, 则实数m 等于( )A ． 3-B ． 33C ．33-或3D ．33-或33【答案】C3．若直线3)1(:1=-+y a ax l 与2)32()1(:2=++-y a x a l 互相垂直，则a 的值为( )A ．－3B ．1C ．0或－23D ．1或－3【答案】D4．已知点(2,3),(3,2)A B --，若直线l 过点(1,1)P 与线段AB 相交，则直线l 的斜率k 的取值范围是( )A ．34k ≥B ．324k ≤≤C ．324k k ≥≤或 D ．2k ≤ 【答案】C5．直线xsin β＋ycos θ＝2＋sin θ与圆(x －1)2＋y 2＝4的位置关系是( )A ．相离B ．相切C ．相交D ．以上都有可能 【答案】B6．直线3440x y --=被圆22(3)9x y -+=截得的弦长为( ) A ．22 B ． 42C ．4D ．2【答案】B7．圆012222=+--+y x y x 上的点到直线2=-y x 的距离最大值是( )A ． 2B ． 21+C ． 221+D ． 221+【答案】B8．一条光线从点M （5，3）射出，与x 轴的正方向成α角，遇x 轴后反射，若3tan =α，则反射光线所在的直线方程为( )A ．123-=x yB ．123--=x yC ．123+=x yD ．123+-=x y【答案】D9．如果把圆沿向量平移到,且与直线相切,则的值为( )A ．2或－B ．2或C ．－2或D ．－2或－【答案】A10．已知两条直线2-=ax y 和01)2(3=++-y a x 互相平行，则a 等于( )A ．1或-3B ．-1或3C ．1或3D ．-1或3 【答案】A11．已知入射光线所在直线的方程为2x-y-4=0，经x 轴反射，则反射光线所在直线的方程是( )A ．24y x =--B ．24y x =-+C ．112y x =+ D ．112y x =-- 【答案】B12．已知圆O 的半径为1，PA 、PB 为该圆的两条切线，A 、B 为两切点，那么PA PB •的最小值为( )A ． 42-+B ．32-+C ．422-+D ．322-+【答案】D第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．直线y ＝x ＋b 与曲线21y x -=恰有一个交点，则实数的b 的取值范围是____________ 【答案】}2{]1,1(--14．已知AC BD 、为圆O :224x y +=的两条相互垂直的弦，垂足为()1,2M ,则四边形ABCD 的面积的最大值为 。

高考一轮复习备考试题直线与圆一、填空题1、（2014年江苏高考）在平面直角坐标系xOy 中，直线032x =-+y 被圆4)1(2x 22=++-y ）（截得的弦长为 ▲ ．2、（2012年江苏高考）在平面直角坐标系xOy 中，圆C 的方程为228150x y x +-+=，若直线2y kx =-上至少存在一点，使得以该点为圆心，1为半径的圆与圆C 有公共点，则k 的最大值是 ▲ ． 3、（2015届江苏南通市直中学高三9月调研）已知圆22:24200C x y x y +---=，直线l 过点P （3，1），则当直线l 被圆C 截得的弦长最短时，直线l 的方程为 ▲4、（2015届江苏苏州高三9月调研）已知圆()()()22:10C x a y a a -+-=>与直线3y x =相交于,P Q 两点,则当CPQ ∆的面积最大时,此时实数a 的值为 ▲5、（南京市2014届高三第三次模拟）在平面直角坐标系xOy 中，圆C 的方程为(x －1)2＋y 2＝4，P 为圆C 上一点．若存在一个定圆M ，过P 作圆M 的两条切线PA ，PB ，切点分别为A ，B ，当P 在圆C 上运动时，使得∠APB 恒为60︒，则圆M 的方程为6、（南通市2014届高三第三次调研）在平面直角坐标系xOy 中，圆C 的方程为2240x y x +-=．若直线(1)y k x =+上存在一点P ，使过P 所作的圆的两条切线相互垂直，则实数k 的取值范围是 ▲ ．7、（2014江苏百校联考一）已知圆22:(2)1C x y -+=，点P 在直线:10l x y ++=上，若过点P 存在直线m 与圆C 交于A 、B 两点，且点A 为PB 的中点，则点P 横坐标0x 的取值范围是 ．8、（南通市2014届高三第二次模拟）在平面直角坐标系xOy 中，设A 是半圆O ：222x y +=（0x ≥）上一点，直线OA 的倾斜角为45°，过点A 作x 轴的垂线，垂足为H ，过H 作OA 的平行线交半圆于点B ，则直线AB 的方程是 ▲9、（南京、盐城市2014届高三第二次模拟（淮安三模））在平面直角坐标系xOy 中，过点P (5，3)作直线l 与圆x 2＋y 2＝4相交于A ，B 两点，若OA ⊥OB ，则直线l 的斜率为 ▲ 10、（苏锡常镇四市2014届高三3月教学情况调研（一））在平面直角坐标系xOy 中，已知点(3,0)P 在圆222:24280C x y mx y m +--+-=内，动直线AB 过点P 且交圆C 于,A B 两点，若△ABC 的面积的最大值为16，则实数m 的取值范围为 ▲11、（江苏省诚贤中学2014届高三12月月考）垂直于直线1y x =+且与圆221x y +=相切于第一象限的直线方程是 ▲12、（江苏省灌云高级中学2014届高三第三次学情调研）已知点Q b a p 与点),(（1，0）在直线0132=+-y x 的两侧，则下列说法（1）0132>+-b a （2）0≠a 时，ab有最小值，无最大值 （3）M b a R M >+∈∃+22,使恒成立 （4）且0>a 1≠a ,时0>b , 则1-a b 的取值范围为（-),32()31,∞+⋃-∞ 其中正确的是 （把你认为所有正确的命题的序号都填上）二、解答题1、（2013年江苏高考）本小题满分14分。