霍尔效应及用其理论测量半导体材料的性能
- 格式:doc
- 大小:1.25 MB
- 文档页数:15

1半导体材料导电类型的测定半导体材料是一类介于导体和绝缘体之间的材料,其导电类型则可以根据能带结构和杂质掺杂来确定。
在本文中,我们将讨论半导体材料导电类型的测定以及导电类型的转变。
半导体材料的导电类型主要分为p型和n型。
在纯净的半导体材料中,只有少量的自由电子和空穴能够参与导电,因此电导率较低。
但是通过掺杂可以增加半导体材料的导电性能。
p型半导体是通过在半导体基体中引入少量的杂质原子,如三价元素硼(B),来增加半导体中的空穴浓度。
在掺杂过程中,原来的半导体材料(如硅或锗)会失去一个电子,形成一个不满的能带,同时该杂质原子会提供一个空穴,使得材料呈现p型导电特性。
n型半导体是通过在半导体基体中引入少量的杂质原子,如五价元素磷(P)或硼(B),来增加半导体中的自由电子浓度。
在这种情况下,杂质原子会提供一个额外的电子,使得材料呈现n型导电特性。
为了确定半导体材料的导电类型,可以使用多种实验方法:1.霍尔效应测量:霍尔效应是利用半导体材料中的电子和空穴对载流子移动的方式进行测量。
通过施加一个横向磁场,可以观察到横向电场产生的电压。
根据这个电压的正负和大小,可以确定半导体材料的导电类型。
2.热平衡法:通过测量材料在不同温度下的电导率,可以确定其导电类型。
如果电导率随着温度的升高而增加,则说明该材料为n型导电;如果电导率随着温度的升高而减小,则说明该材料为p型导电。
3.半导体电极测量:通过在半导体材料的不同位置上放置电极,并通过测量电极上的电流来确定导电类型。
如果在电极之间存在电流,则说明该材料为n型导电;如果在电极外部存在电流,则说明该材料为p型导电。
除了以上的方法,还可以利用光电导性测量法、霍尔电压测量法等来确定半导体材料的导电类型。
在实际应用中,半导体材料的导电类型可以通过掺杂方法进行调控。
通过合适的杂质元素掺杂以及掺杂浓度的控制,可以改变半导体材料的导电类型,从而满足不同的应用需求。
综上所述,半导体材料的导电类型可以通过多种实验方法来确定,包括霍尔效应测量、热平衡法和半导体电极测量等。

半导体的霍尔系数与电导率的测量引言1879年,霍尔(E.H.Hall)研究通有电流的导体在磁场中受力时,发现在垂直于磁场和电流的方向上产生了电动势,这个电磁效应称为“霍尔效应”。
在半导体材料中,霍尔效应比在金属中大几个数量级,引起人们对它的深入研究。
霍尔效应的研究在半导体理论的发展中起了重要的推动作用。
直到现在,霍尔效应的测量仍是研究半导体性质的重要实验方法。
利用霍尔系数和电导率的联合测量,可以用来研究半导体的导电机构(本征导电和杂质导电)、散射机构(晶格散射和杂质散射),并可以确定半导体的一些基本参数,如:半导体材料的导电类型、载流子浓度、迁移率大小、禁带宽度、杂质电离能等。
利用霍尔效应制成的元件,称为霍尔元件,也已广泛地用于测试仪器和自动控制系统中。
实验原理1.霍尔效应和霍尔系数设一块半导体的x方向上有均匀的电流Ix流过,在z方向上加有磁场Bz,则在这块半导体的y方向上出现一横向电势差UH,这种现象被称为“霍尔效应”,UH称为“霍尔电压”,所对应的横向电场E H称为“霍尔电场”。
见图6.1-1。
实验指出,霍尔电场强度E H的大小与流经样品的电流密度Jx和磁感应强度Bz的乘积成正比E H=R H·Jx·Bz(6.1-1)式中比例系数RH称为“霍尔系数”。
下面以p型半导体样品为例,讨论霍尔效应的产生原理并推导、分析霍尔系数的表达式。
半导体样品的长、宽、厚分别为L、a、b,半导体载流子(空穴)的浓度为p,它们在电场E x作用下,以平均漂移速度vx沿x方向运动,形成电流Ix。
在垂直于电场E x方向上加一磁场Bz,则运动着的载流子要受到洛仑兹力的作用F=q×B(6.1-2)式中q为空穴电荷电量。
该洛仑兹力指向-y方向,因此载流子向-y方向偏转,这样在样品的左侧面就积累了空穴,从而产生了一个指向+y方向的电场—霍尔电场E y。
当该电场对空穴的作用力qEy与洛仑兹力相平衡时,空穴在y方向上所受的合力为零,达到稳态。

霍尔效应及其应用实验原理霍尔效应是一种利用材料内部自由电子的磁场运动所引起的电压现象,也是一种用来测量磁场强度和磁场方向的技术。
该效应可以在所有导体材料中观察到,尤其是在半导体材料中表现出更为复杂的特性。
霍尔效应的实验原理是:当一个导体材料处于垂直于磁场方向的磁场中,自由电子的运动受到磁场的力作用而偏向一侧,形成电荷分离,从而产生电势差,这个电势差称为霍尔电势差。
霍尔电势差与磁场的大小和电流的方向有关。
一般来说,当电流方向与磁场垂直时,霍尔电势差达到最大值;当电流方向与磁场平行时,霍尔电势差为零。
霍尔效应在实际应用中有着广泛的用途,包括测量磁场强度和方向、测量导体材料内部自由电子浓度、测量射线辐照量等。
在半导体材料中,霍尔效应可以用来测量载流子类型、载流子浓度以及半导体的类型等。
在实验中,霍尔效应的应用可以通过霍尔元件进行。
霍尔元件通常是一个纯半导体片,在片的交叉口处引入掺杂杂质,使其形成p型和n型结构,从而形成一个p-n结。
当通过霍尔元件的电流和磁场垂直时,就可以观察到霍尔电势差的产生。
具体实验步骤如下:1.准备霍尔元件。
将霍尔元件插入电路板的插孔中,连接元件的负载电阻。
2.设置磁场。
将磁铁放在电路板上方并打开电源,调整磁铁的位置和方向,使磁场垂直于霍尔元件。
3.测量电压。
开启电源,调节电流大小,记录不同电流下霍尔电压的大小和方向。
4.绘制图表。
将电流和霍尔电压数据绘制成图表,根据图表分析霍尔电势差与电流和磁场的关系。
霍尔效应具有广泛的应用前景,特别是在微电子工业中,可以用来测量半导体性能和器件参数,从而提高半导体器件制造的精度和可靠性。

实验三半导体材料的霍尔效应测量实验1实验原理1)霍尔效应霍尔效应指的是在外加磁场的作用下,给半导体通入电流,内部的载流子受到磁场引起的洛伦兹力的影响,空穴和电子向相反的方向偏转,这种偏转导致在垂直电流和磁场方向上产生正负电荷的积累,形成附加的横向电场,直至电场对载流子的作用力与洛伦兹力抵消,此时的电场强度乘以半导体样品的宽度后,可以得到霍尔电压V H。
设磁感应强度为B,电子浓度(假设为n型半导体)为n,则电流表达式为I H=nevbd,而霍尔电压产生的电场为E H=vB霍尔电压的表达式为:V H=E H b=vBb =I HnebdBb =1neI H Bd=R HI H Bd其中R H称为霍尔系数:R H=1 ne可以通过V H,B, I H的方向可以判断样品的导电类型,通过V H和 I H的关系曲线可以提取出R H,进一步还可以得到电子(空穴)浓度。
在实际测量中,还会伴随一些热磁副效应,使得V H还会附带另外一些电压,给测量带来误差。
为了消除误差,需要取不同的I H和B的方向测量四组数据求平均值得到V H,如下表示I H正向I H负向B正向V1V3B负向V2V42)范德堡法测量电阻率由于实验使用的霍尔元件可视为厚度均匀、无空洞的薄片,故可使用范德堡法进行电阻率的测量。
在样品四周制作四个极小的欧姆接触电极1,2,3,4。
如图2所示。
14图 1 霍尔效应原理示意图先在1、2端通电流,3、4端测电压,可以定义一个电阻R1=|V34| I12然后在2、3端通电流,1、4端测电压,求R2=|V14| I23理论上证明样品的电阻率与R1、R2的关系为ρ=πdln2R1+R22f可以通过查表可知范德堡因子f与R1/R2的关系,从而求得样品的电阻率。
2实验内容本实验所用仪器为SH500-A霍尔效应实验仪、恒流电源、高斯计。
实验步骤如下:1)连线掌握仪器性能,连接恒流电源与霍尔效应试验仪之间的各组连线。
2)测量霍尔系数,判断样品的导电类型测量半导体样品的霍尔系数。

半导体霍尔系数与电导率测量实验报告实验目的:1.了解半导体材料的霍尔效应原理及其在物理中的应用;2.学习使用霍尔测量仪器测量半导体样品的霍尔系数和电导率。
实验仪器和材料:1.霍尔效应实验装置2.N型半导体样品3.针对净电荷携带型的霍尔探头4.模拟多用表5.直流电源实验原理:霍尔效应是指在电流通过垂直于磁场和电流方向的导体时,引起的横向电场现象。
在半导体材料中,载流子(电子或空穴)在外加磁场下发生漂移运动,从而在横向形成一电场,这个现象称为霍尔效应。
霍尔效应与材料的类型(N型或P型)、载流子类型(电子或空穴)、载流子浓度和电导率等因素有关。
霍尔系数与电导率有着密切的关系。
霍尔系数RH的定义为,当载流子在单位尺寸、单位载流密度和单位磁感应强度下受到的洛伦兹力,与单位电场大小的比值。
电导率σ与半导体样品的电阻率ρ之间有如下关系:σ=1/ρ。
因此,通过测量霍尔系数和电阻率,可以确定半导体材料的电导率。
实验步骤:1.将霍尔样品插入霍尔探头中,确保霍尔探头正面与样品接触良好。
2.将多用表调至电压测量模式并连接至霍尔探头,用以测量霍尔电压。
将直流电源连接至样品和导线,调整电压和电流的大小。
3.调节磁场大小,将霍尔探头放置于磁场中,使其垂直于电流方向。
记录多用表上的霍尔电压和电流读数。
4.重复步骤3,分别调整电流方向为正和负,记录相应的霍尔电压和电流读数。
5.根据测量得到的数据,计算霍尔系数和电导率。
实验结果:根据实验测得的数据,计算得到霍尔系数和电导率。
实验讨论与分析:1.对实验结果进行合理性分析,比较不同试样的霍尔系数和电导率。
结论:通过实验测量分析,得到了半导体样品的霍尔系数和电导率。
同时,对实验结果进行分析和讨论,深入理解了霍尔效应在半导体材料中的应用。

半导体霍尔测试摘要:一、半导体霍尔效应测试的基本原理二、半导体霍尔效应测试的应用三、半导体霍尔效应测试的优缺点四、半导体霍尔效应测试的发展前景正文:一、半导体霍尔效应测试的基本原理半导体霍尔效应测试是一种测量半导体材料内部性质的有效方法。
霍尔效应是指在磁场中,运动的带电粒子(电子或空穴)受到洛仑兹力作用而发生偏转的现象。
当带电粒子被约束在固体材料中,这种偏转会导致在垂直于电流和磁场的方向上产生正负电荷的聚积,形成附加的横向电场。
霍尔效应测试正是利用这一现象来测量半导体材料的电学性质。
二、半导体霍尔效应测试的应用半导体霍尔效应测试在许多领域都有广泛应用,包括:1.确定材料的禁带宽度和杂质电离能:通过测量霍尔系数及其与温度的关系,可以计算出载流子的浓度,从而确定材料的禁带宽度和杂质电离能。
2.确定材料的电阻率:通过霍尔系数和电阻率的联合测量,可以确定材料的电阻率。
3.检测材料的缺陷和界面质量:半导体霍尔效应测试可以检测材料的缺陷和界面质量,这对于制程工艺的优化和产品质量的保证具有重要意义。
三、半导体霍尔效应测试的优缺点半导体霍尔效应测试具有以下优点:1.非接触测量:霍尔效应测试无需与被测材料直接接触,因此可以避免对材料表面造成损伤。
2.测量范围广:霍尔效应测试可以测量各种类型的半导体材料,包括晶体、薄膜和纳米材料等。
3.测量精度高:霍尔效应测试具有较高的测量精度,可以满足各种应用场景的需求。
然而,半导体霍尔效应测试也存在一些缺点:1.受磁场影响:霍尔效应测试的结果受到磁场强度和方向的影响,因此在测量过程中需要控制磁场。
2.温度依赖性:霍尔效应测试的结果具有温度依赖性,需要考虑温度对测量结果的影响。
四、半导体霍尔效应测试的发展前景随着科学技术的发展,半导体霍尔效应测试在材料研究、集成电路设计和制造等领域将发挥越来越重要的作用。


举例霍尔效应在半导体材料研究中的应用
霍尔效应是一种物理效应,在半导体材料研究中有着广泛的应用,特别是在电学性质的研究方面。
半导体材料在外部电场的作用下会发生电流,但通常情况下,这
个电流是由电子和空穴共同带电导致的。
然而,通过霍尔效应的研究,我们可以独立地测量电子和空穴在材料中移动的速度和密度。
在半导体器件的制造中,霍尔效应可以被用来测量材料的导电性质。
通过测量霍尔电压和外加磁场的关系,我们可以得到材料的移动
载流子浓度和电子迁移率等参数,这些参数对于半导体器件的性能设
计和优化至关重要。
此外,霍尔效应还被用于研究半导体材料的磁性质。
例如,研究
磁随机存取器(MRAM)的制造过程,霍尔效应可以用来检验铁磁性和
反铁磁性材料之间的界面和磁阻的质量。
总之,霍尔效应在半导体材料研究中具有广泛的应用,不仅可以
帮助我们了解材料的电性、磁性质,还可以对半导体器件的制造和设
计提供重要的指导。
实验报告
一、实验目的和任务
1.理解霍尔效应的物理意义;
2.了解霍尔元件的实际应用;
3.掌握判断半导体导电类型,学会测量半导体材料的霍尔系数、电导率、载流子浓度、漂移迁移率及霍
尔迁移率的实验方法。
二、实验原理
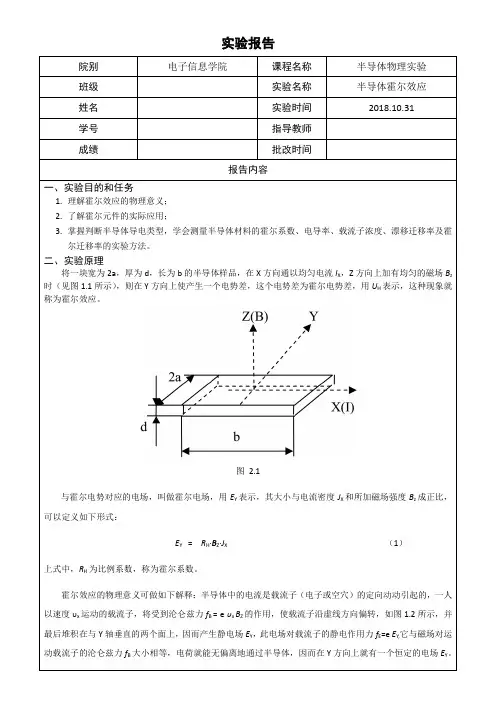
将一块宽为2a,厚为d,长为b的半导体样品,在X方向通以均匀电流I X,Z方向上加有均匀的磁场B z 时(见图1.1所示),则在Y方向上使产生一个电势差,这个电势差为霍尔电势差,用U H表示,这种现象就称为霍尔效应。
图 2.1
与霍尔电势对应的电场,叫做霍尔电场,用E Y表示,其大小与电流密度J X和所加磁场强度B z成正比,可以定义如下形式:
E Y = R H·B Z·J X(1)
上式中,R H为比例系数,称为霍尔系数。
霍尔效应的物理意义可做如下解释:半导体中的电流是载流子(电子或空穴)的定向动动引起的,一人以速度υx运动的载流子,将受到沦仑兹力f B = e υx B Z的作用,使载流子沿虚线方向偏转,如图1.2所示,并最后堆积在与Y轴垂直的两个面上,因而产生静电场E Y,此电场对载流子的静电作用力f E=e E Y,它与磁场对运动载流子的沦仑兹力f B大小相等,电荷就能无偏离地通过半导体,因而在Y方向上就有一个恒定的电场E Y。

霍尔效应及其参数测定实验报告本实验主要介绍了霍尔效应及其参数测定的实验方法。
实验采用霍尔元件通过外磁场产生霍尔电势,从而测定材料的电导率、载流子浓度和载流子迁移率等参数。
实验结果表明,霍尔效应可以非常有效地测量半导体材料的电学特性,是一种重要的研究手段。
关键词:霍尔效应,霍尔元件,电导率,载流子浓度,载流子迁移率一、实验目的1.了解霍尔效应的基本原理2.掌握霍尔元件的制备方法3.掌握霍尔效应参数的测定方法4.学会使用实验仪器进行实验操作二、实验原理霍尔效应是指在磁场中,电流流动的导体中会出现电势差现象。
当磁场方向与电流方向垂直时,将产生垂直于两个方向的霍尔电势。
这种现象被称为霍尔效应。
霍尔电势的大小与电流、磁场及材料的特性有关。
霍尔元件是用于测量霍尔效应的元件。
霍尔元件通常由半导体材料制成,其结构为一个平面小矩形,两端连接电极,垂直于平面的方向中心处有一个小孔,可以通过孔内通入磁场。
当通入磁场时,材料中的载流子会受到洛伦兹力的作用,使载流子在材料中产生偏移,从而导致霍尔电势的产生。
通过测量霍尔电势的大小以及施加磁场的大小和方向,可以确定材料的电导率、载流子浓度和载流子迁移率等参数。
三、实验步骤1.制备霍尔元件首先,将半导体材料切割成小片,然后将其表面进行化学处理,以便在其表面上生长一层厚度为几微米的氧化层。
接着,将元件在高温下进行烘烤,使氧化层形成一种结构,即霍尔元件的结构。
最后在两端连接电极,制成完整的霍尔元件。
2.测量霍尔电势将霍尔元件放入测量器中,通入一定电流,然后施加一定磁场,记录霍尔电势的大小。
3.测量电阻率在不施加磁场的情况下,通过测量电流和电压的大小,计算出材料的电阻率。
4.计算载流子浓度和迁移率通过测量霍尔电势的大小、电阻率和电子电荷数,可以计算出载流子浓度和迁移率等参数。
四、实验结果与分析通过实验测量,得到了不同条件下的霍尔电势大小和材料的电阻率。
通过计算,得到了材料的电导率、载流子浓度和迁移率等参数。

霍尔效应实验报告研究金属和半导体材料的霍尔电压差异摘要:本实验以霍尔效应为基础,研究金属和半导体材料的霍尔电压差异。
通过不同材料的测试,测量霍尔电压,并分析金属和半导体材料的特点及其在实际应用中的潜在价值,为进一步应用此技术提供理论依据。
引言:霍尔效应指的是当电流通过垂直于表面的导体材料时,由于外加磁场引起的电子偏转,产生一种霍尔电压的现象。
金属和半导体材料在电子结构和导电性方面存在差异,因此也会出现不同的霍尔电压差异。
本实验旨在通过实际测量,探究金属和半导体材料的霍尔电压现象,为进一步研究使用此技术提供参考。
实验器材:1.霍尔效应实验装置2.金属材料(如铜、铝等)3.半导体材料(如硅、锗等)4.直流电源5.磁铁6.万用表实验步骤:1.搭建霍尔效应实验装置,将金属和半导体材料分别连接到实验装置的电路中。
2.调节直流电源,使得电流保持一定的数值,记录电流数值并保持不变。
3.通过调节磁铁的位置和磁场强度,使得霍尔电压最大化。
4.使用万用表测量和记录霍尔电压的数值。
5.重复步骤2至4,对比金属和半导体材料的霍尔电压数值。
结果与讨论:通过多次实验得到的数据,我们可以看到金属和半导体材料的霍尔电压差异。
金属材料的霍尔电压数值相对较小,且相对稳定;而半导体材料的霍尔电压数值相对较大,且在不同条件下存在较大波动。
这与金属和半导体材料的电子结构和导电特性密切相关。
金属材料的霍尔电压较小的原因是,金属中的自由电子密度较高,电子在外加磁场作用下容易产生偏转,从而引起霍尔电压的生成。
而半导体材料由于其特殊的电子结构,自由电子的密度较低,因此需要更大的外加磁场才能引起霍尔电压的生成。
此外,半导体材料由于杂质和缺陷的存在,使得霍尔电压的数值在不同条件下存在较大的波动。
金属和半导体材料的霍尔电压差异为实际应用提供了潜在价值。
金属材料的小霍尔电压适合在对电压要求较高、精度要求较低的场合中使用。
而半导体材料的较大霍尔电压可以用于传感器等需要高灵敏度的设备中。
半导体霍尔系数与电导率测量实验报告实验目的:1.了解半导体材料的基本性质,包括霍尔效应和电导率;2.通过实验测量半导体材料的霍尔系数和电导率,分析其导电性质。
实验原理:1.霍尔效应:当在半导体材料中施加电流时,电子受到洛伦兹力的作用会发生偏转,并在材料的一侧积累负电荷,另一侧积累正电荷。
这种电荷积累导致的电压差称为霍尔电压,霍尔电压与施加的电场、电流以及材料的导电性质有关。
霍尔系数RH表示霍尔电压与电流、电场的关系。
当材料处于均匀磁场中时,可以通过测量霍尔电压和电流得到霍尔系数。
2.电导率:电导率是描述材料导电性质的一个参数,通常用σ表示。
电导率与材料的电阻率ρ和材料的导电性质有关。
电导率可以通过测量材料的电阻率和材料的几何尺寸来计算,也可以通过测量材料的电导和电流来得到。
实验仪器:1.霍尔效应实验装置,包括霍尔电压源、电流源、恒磁场装置等;2.电导率测量设备,包括电阻计、示波器等。
实验步骤:1.霍尔系数测量:a.调节霍尔电压源和电流源,使得电流通过样品,同时使恒磁场施加在样品上;b.测量霍尔电压随电流变化的关系,计算得到霍尔系数。
2.电导率测量:a.连接电阻计和示波器,将待测样品接入电路;b.测量电流和电压随时间变化的关系,并根据测得的电压和电流计算得到电阻率;c.根据材料的几何尺寸,计算得到电导率。
实验结果:根据实验所得数据计算得到半导体材料的霍尔系数和电导率,并记录在下表中:实验样品,霍尔系数(RH),电导率(σ)---------,-------------,-----------------样品1,2.3x10^-3,1.5x10^3S/m样品2,1.8x10^-3,2.1x10^3S/m样品3,2.1x10^-3,1.8x10^3S/m实验讨论:通过实验测量得到的霍尔系数和电导率可以反映半导体材料的导电性质。
从实验结果可知,样品1的霍尔系数和电导率最小,样品2次之,样品3最大。
这说明样品3的导电性能最好,样品1的导电性能最差。
霍尔效应摘要:霍尔效应是研究半导体材料性能的基本方法。
通过霍尔效应实验测定的霍尔系数能够判断半导体导电类型、载流子浓度及载流子迁移率等重要参数。
关键词:霍尔效应,霍尔系数,重要参数一、引言霍尔效应在当今科学技术的许多领域都有着广泛的应用,如测量技术、电子技术、自动化技术。
霍尔效应是磁电效应的一种,这一现象是霍尔于1879年在研究金属方面的导电结构时发现的,经过约100年后德国物理学家克利青(Klaus von Klitzing, 1943-)等在研究极低温度和强磁场中的半导体时发现了量子霍尔效应之后,美籍华裔物理学家崔琦(Daniel Chee T sui,1939- )和美国物理学家劳克林(Robert ughlin,1950-)、施特默(Horst L. St rmer,1949-)在更强磁场下研究量子霍尔效应时发现了分数量子霍尔效应,2013年,由清华大学薛其坤院士领衔,清华大学、中科院物理所和斯坦福大学研究人员联合组成的团队在量子反常霍尔效应研究中取得重大突破,他们从实验中首次观测到量子反常霍尔效应。
“量子反常霍尔效应”并不仅是一个云里雾里的科学名词,它还意味着某种科幻小说搬的未来生活;若这项发现能投入应用,超级计算机将有可能成为Ipad大小的掌上笔记本,智能手机内存也许会超过目前最先进产品的上千倍,除了超长时间待机外,还将拥有当代人无法想象的快递。
这使得霍尔效应具有很大的研究价值,本文主要阐述了霍尔效应的原理,霍尔效应研究的步骤,方法,及相关领域的应用。
二、实验内容2.1实验仪器霍尔效应实验仪,主要由电磁铁,样品式样,样品架,Is和IM换向开关,VH和V0测量选择开关组成。
霍尔效应测试仪,主要由样品工作电流源、励磁电流源和直流数字毫伏表组成2.2 实验原理图A 霍尔效应示意图如图A所示的样品薄片,若在它的两端通以控制电流I,并在薄片的垂直于施加磁感应强度为B的磁场,那么,在垂直于电流和磁场的方向上(即霍尔输出端之间)将产生电势差UH,称为霍尔电压,这种现象称为霍尔效应。
实验三霍尔效应法测量半导体的载流子浓度、电导率和迁移率一、实验目的1.了解霍尔效应实验原理以与有关霍尔元件对材料要求的知识。
2.学习用“对称测量法”消除副效应的影响,测量并绘制试样的 VH-IS 和VH-IM 曲线。
3.确定试样的导电类型、载流子浓度以与迁移率。
二、实验原理霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。
当带电粒子(电子或空穴)被约束在固体材料中,这种偏转就导致在垂直电流和磁场的方向上产生正负电荷的聚积,从而形成附加的横向电场,即霍尔电场。
对于图(1)(a)所示的 N 型半导体试样,若在 X 方向的电极 D、E 上通以电流 Is,在 Z 方向加磁场 B,试样中载流子(电子)将受洛仑兹力:其中 e 为载流子(电子)电量, V为载流子在电流方向上的平均定向漂移速率,B 为磁感应强度。
无论载流子是正电荷还是负电荷,Fg 的方向均沿 Y 方向,在此力的作用下,载流子发生便移,则在 Y 方向即试样 A、A´电极两侧就开始聚积异号电荷而在试样 A、A´两侧产生一个电位差 VH,形成相应的附加电场 E—霍尔电场,相应的电压 VH 称为霍尔电压,电极 A、A´称为霍尔电极。
电场的指向取决于试样的导电类型。
N 型半导体的多数载流子为电子,P 型半导体的多数载流子为空穴。
对 N 型试样,霍尔电场逆 Y 方向,P 型试样则沿Y 方向,有显然,该电场是阻止载流子继续向侧面偏移,试样中载流子将受一个与 Fg方向相反的横向电场力:其中 EH 为霍尔电场强度。
FE 随电荷积累增多而增大,当达到稳恒状态时,两个力平衡,即载流子所受的横向电场力 e EH 与洛仑兹力eVB相等,样品两侧电荷的积累就达到平衡,故有设试样的宽度为 b,厚度为 d,载流子浓度为 n,则电流强度V Is 与的关系为由(3)、(4)两式可得即霍尔电压 VH(A、A´电极之间的电压)与 IsB 乘积成正比与试样厚度 d成反比。
实验三霍尔效应法测量半导体的载流子浓度、电导率和迁移率一、实验目的1.了解霍尔效应实验原理以与有关霍尔元件对材料要求的知识。
2.学习用“对称测量法”消除副效应的影响,测量并绘制试样的 VH-IS 和VH-IM 曲线。
3.确定试样的导电类型、载流子浓度以与迁移率。
二、实验原理霍尔效应从本质上讲是运动的带电粒子在磁场中受洛仑兹力作用而引起的偏转。
当带电粒子(电子或空穴)被约束在固体材料中,这种偏转就导致在垂直电流和磁场的方向上产生正负电荷的聚积,从而形成附加的横向电场,即霍尔电场。
对于图(1)(a)所示的 N 型半导体试样,若在 X 方向的电极 D、E 上通以电流 Is,在 Z 方向加磁场 B,试样中载流子(电子)将受洛仑兹力:其中 e 为载流子(电子)电量, V为载流子在电流方向上的平均定向漂移速率,B 为磁感应强度。
无论载流子是正电荷还是负电荷,Fg 的方向均沿 Y 方向,在此力的作用下,载流子发生便移,则在 Y 方向即试样 A、A´电极两侧就开始聚积异号电荷而在试样 A、A´两侧产生一个电位差 VH,形成相应的附加电场 E—霍尔电场,相应的电压 VH 称为霍尔电压,电极 A、A´称为霍尔电极。
电场的指向取决于试样的导电类型。
N 型半导体的多数载流子为电子,P 型半导体的多数载流子为空穴。
对 N 型试样,霍尔电场逆 Y 方向,P 型试样则沿Y 方向,有显然,该电场是阻止载流子继续向侧面偏移,试样中载流子将受一个与 Fg方向相反的横向电场力:其中 EH 为霍尔电场强度。
FE 随电荷积累增多而增大,当达到稳恒状态时,两个力平衡,即载流子所受的横向电场力 e EH 与洛仑兹力eVB相等,样品两侧电荷的积累就达到平衡,故有设试样的宽度为 b,厚度为 d,载流子浓度为 n,则电流强度V Is 与的关系为由(3)、(4)两式可得即霍尔电压 VH(A、A´电极之间的电压)与 IsB 乘积成正比与试样厚度 d成反比。
变温霍尔效应测量半导体电学特性霍尔效应的测量是研究半导体性质的重要实验方法。
利用霍尔系数和电导率的联合测量,可以用来确定半导体的导电类型和载流子浓度。
通过测量霍尔系数与电导率随温度的变化,可以确定半导体的禁带宽度、杂质电离能及迁移率的温度系数等基本参数。
本实验通过对霍尔样品在弱场条件下进行变温霍尔系数和电导率的测量,来确定半导体材料的各种性质。
【实验目的】1.了解半导体中霍尔效应的产生机制。
2.通过实验数据测量和处理,判别半导体的导电类型,计算室温下样品的霍尔系数、电导率、迁移率和载流子浓度。
3.掌握变温条件下霍尔系数和电阻率的测量方法,了解两者随温度的变化规律。
【实验仪器】本实验采用CVM200变温霍尔效应测试系统来完成,本仪器系统由可换向永磁体、CME12H变温恒温器、TC202控温仪、CVM-200霍尔效应仪等组成。
本系统自带有两块样品,样一是美国Lakeshore公司HGT-2100高灵敏度霍尔片,厚度为0.18mm,最大工作电流≤10 mA,室温下的灵敏度为55-140 mV/kG; 样二为锑化铟,厚度为1.11mm,最大电流为60mA,其在低温下是典型的P型半导体,而在室温下又是典型的N型半导体,相应的测试磁场并不高,但霍尔电压高,降低了对系统仪表灵敏度、磁铁磁场的要求。
【实验原理】1.霍尔效应和霍尔系数ZYX图1 霍尔效应示意图霍尔效应是一种电流磁效应(如图1)。
当半导体样品通以电流Is ,并加一垂直于电流的磁场B ,则在样品两侧产生一横向电势差U H ,这种现象称为“霍尔效应”,U H 称为霍尔电压,d B I R H S H U =(1)则: IsB d U H H R =(2) R H 叫做霍尔系数,d 为样品厚度。
对于P 型半导体样品, qp H R 1= (3)式中q 为空穴电荷电量,p 为半导体载流子空穴浓度。
对于n 型半导体样品,qn H R 1-= (4)式中为n 电子电荷电量。
本科毕业论文题目:霍尔效应及用其理论测量半导体材料的性能学院:物理与电子科学院班级: 09级物理二班姓名:闫文斐指导教师:付仁栋职称:讲师完成日期: 2013 年 5 月 15 日霍尔效应及用其理论测量半导体材料的性能摘要:简述了霍尔效应的基本原理,测量判定半导体材料的霍尔系数,确定半导体材料的导电类型、载流子浓度及迁移率。
因此,霍尔效应时研究半导体性质的重要实验方法。
分析了利用霍尔效应测量半导体特性参数中影响的重要副效应,给出了减小或消除这些副效应的方法,并在实验中,对实验仪器进行了一定得改进,使实验更有利于操作。
关键字:霍尔效应;半导体;副效应;载流子;改进目录引言 (1)1. 霍尔效应 (2)1.1霍尔效应的基本原理 (2)1 .2 霍尔电势差和磁场测量 (3)2. 实验内容 (5)2.1 确定霍尔元件的导电类型 (5)2.2 霍尔灵敏度、霍尔系数、载流子浓度的测量 (6)2.3实验数据的处理 (6)3. 误差分析 (8)3.1主要误差及原因 (8)3.2 消除误差的方法 (9)4. 实验的改进 (10)4.2 霍尔元件载流子迁移率μ和电导率σ的测量 (11)5. 结束语 (11)致谢 (11)参考文献 (11)引言霍尔效应是电磁效应在实验中的应用的一中,这是美国的一位伟大的物理学家霍尔(A.H.Hall,1855—1938)发现的,于1879年在探索金属的导电原理时偶然发明的。
将载流霍尔元件置于与其垂直的磁场B中,板内出现的磁场会与电流方向垂直,同样的,板的两边就会出现一个横向电压(如图1)。
在霍尔发现的100年后,1985年德国克利青( K laus von K litzing,1943-)等研究极低温度和强磁场中的半导体时发现量子霍尔效应获得诺贝尔奖。
1998年华裔科学家崔琦(Daniel Chee Tsui,1939-)、斯坦福大学的美国物理学家劳克林(Robert ughlin,1950-)和哥伦比亚大学的施特默(Horst L.Stormer,1949-)在更强磁场下研究量子霍尔效应,因为发现分数量子霍尔效应而荣获诺贝尔奖。
霍尔效应原本的发现是在对金属的研究中, 但在科学发展到现在,却发现该效应在半导体中的应用更加突出, 所以在半导体的研究中一直以来提供非常重要的理论依据。
本文通过霍尔效应测量,不仅判别了半导体材料的导电类型,霍尔系数、载流子浓度及迁移率和电导率等主要的半导体材料的特性参数。
并在分析操作中因受各种副效应的影响,带来的测量准确度的影响,如何避免这些副效应的影响也是很必要的。
因此,本文还对我们的实验元件做了很好的改进,可以通过实验测量的方法直接得到我们所需要的迁移率和电导率。
1.霍尔效应1.1霍尔效应的基本原理当有电流通过霍尔元件时,载流子的漂移运动方向,与它所带电荷的符号有很大的关系。
若载流子为正,她的飘移运动方向即为电流方向;相反,若载流子为负,则它的飘移运动方向是电流的反方向。
若将半导体元件通有电流的同时,再置于电磁场中(所示如图1),半导体片所在的平面与电场方向和磁场方向两两互相垂直,设电流沿x方向,电流大小为I;沿z方向的磁感应强度为B,则在垂直于电场和磁场的y-方向将产生一个如图所示+和y的电场E,我们把这现象称做霍尔效应。
图1 霍尔样品载流子受到洛伦兹力的作用,向半导体一侧聚积。
带正电荷的载流子,它将受到F,如图2(a)所示,导致载流子在A侧聚积,使得半导体沿x方向的磁场作用力m霍尔元件两侧存在电势差,且图中A点电势比B点高。
相反,带负电荷的载流子,如F的方向任沿x轴方向,于是薄片的A侧将聚积大量的图2(b)所示,磁场作用力m复电载流子,使图中A点电势比B点低,则这个电势差称为霍尔电势差。
图2 霍尔效应原理图当电流方向一定时,半导体中载流子所带的电荷正、负决定了A 、B 两点霍尔电势差的符号。
因此,通过测定A 、B 两点的电势差,可以判断霍尔元件中的载流子究竟是带正电荷还是带负电荷。
若载流子为空穴(带正电荷),称为P 型半导体;而载流子为电子(带负电荷),称为N 型半导体。
1 .2 霍尔电势差和磁场测量在霍尔效应中,电荷量为q ,磁场强度为B ,半导体中载流子的飘移速率为v ,则载流子所受磁场为qvB F m = (1)载流子由于受力向半导体一侧聚积,形成横向电场为H E 这横向电场又使得载流子受到电场力H e qE F = (2)的作用。
经判断e F 的方向m F 的方向刚好相反,霍尔电场阻碍载流子的运动,因此载流子不会无限制向半导体侧面漂移下去。
在初始阶段,电场力比磁场力小,载流子向侧面聚积,随着侧面载流子数量的增加,霍尔电场增强,载流子运动速率减小,最终达到平衡,载流子不再运动。
此时m e F F =是表示一种平衡状态。
此时薄片中的横向电场强度为 vB qF q F E me H ===设薄片宽度为a ,则横向电场在A 、B 两点间产生的电势差为v B a a E U H H == (3) 因为j a b I = , qnv j = 所以nqabIv = (4)式中为载流子浓度n ,为电流密度j ,故 n q a bIBE H = (5)所以霍尔电势差n q bIBa E U H H == (6) 令nqR H 1= 为霍尔系数,则bIB R U H H = 所以霍尔系数等于IBbU R H H = (7)由以上理论可以判断半导体具有以下性质:(1)霍尔系数为正,H U >0,则半导体的载流子为空穴(即为P 型半导体),相反载流子为电子,霍尔系数为负,则H U <0。
在实验中测出,霍尔元件I 为电流,B 为感应强度、霍尔电势差H U 、霍尔片厚度为b 值,就可求出霍尔系数H R 值,根据H R 的导电类型正负可以判断半导体的。
(2)载流子浓度n 和霍尔电势差H U 成反比,半导体中载流子浓度n 越大(霍尔系数H R 越小),霍尔电势差H U 就越小。
自由电子一般金属中的载流子为,浓度约为32210cm ,浓度较大,所以金属材料的霍尔效应不明显。
但半导体材料正好相反,得多载流子浓度要比金属小,产生的霍尔电势差很大,即霍尔效应有了很大的使用价值。
(3)根据IBbU nq R H H ==1可得 bqU IBn H =(8)如果知道H U 、I 、B (实验时测得)、用螺旋测微仪测得b ,就可由上式求得霍尔元件的载流子浓度。
2. 实验内容2.1 确定霍尔元件的导电类型设计实验电路如图3所示,○A 为数字电流表,○V 为数字电压表,开关是双掷开关,电源为恒流稳压电源,范围:0~1000mA (可调连续),电路中电阻为21ZX 型电阻箱。
将霍尔元件置于II 型-核磁共振实验装置中。
图3根据测量到的输出电压极性,确定霍尔元件的到点类型。
2.2 霍尔灵敏度、霍尔系数、载流子浓度的测量取电流值,分为8种不同值,在已知的恒定磁场中,测出霍尔电压,注意霍尔元件的额定电流,切勿超过,以防毁坏霍尔元件,纵坐标取H U ,横坐标取I 值作图。
由于实验的系统误差,试验中需要把所测出来的1U 、2U 、3U 、4U 值经过公式44321U U U U U H -+-= (9)运算,直线的斜率为bBR H ,根据已知的B 、b 值,求出霍尔系数H R ,所测的实验数据见图4。
根据bq U IB n H =qR H 1=和已知载流子的电荷量就可以得到该材料的载流子的浓度。
用这个式子可研究温度与浓度的变化规律。
由式(8)可得))(1(IB nqbU H = (10) 令nqbK H 1=(11) 称为霍尔灵敏度,将霍尔元件垂直放入一直磁场中,由测出的霍尔电压和电流,代入H K 值。
2.3实验数据的处理实验记录数据霍尔电压数据:电流表 示数 (mA ) 电压表示数U (mV ) 平均 (U )IU(Ω)B + B - I + I - I +I -00.86.687.68-0.78- 0.78 3.73 16.9 00.7 1.60 1.60- 0.68- 9.67 0.64 14.9 00.63.513.51-4.58- 3.589.5415.900.57.428.42- 5.48-4.48 6.45 12.9 00.41.342.34- 5.38- 5.353.36 08.9 00.37.257.25- 8.28-7.282.2707.900.20.171.17-2.19- 1.19 1.18 05.900.13.84.8-4.9- 3.98.88.800.0 00.0-0.0-0.00.0平均I U11.9图4电流表示数为1.00mA 的那一行数据误差太大,属于坏值,舍掉。
绘制H U I -图见图5图 51. 取出两点求出图线的斜率,进而求出H R 、H K 。
2. 由H R 求载流子浓度n ,由式ne R H 1=得eR n H 1= 这里应该提出,这个关系是不够准确的,须在假定所有载流子的飘移速率都相同的情况下才准确,事实上,载流子的飘移速率服从统计分布,需要引入修正因子83π(),但是这个影响很微小,可以忽略不计。
3. 载流子迁移率的计算厚度为d ,宽度为b 的样品,通过电流为S I 时,测得长度为L (mm 00.5)的霍尔元件上的电压为0V ,测得的的电阻S I V R 0=。
由于电阻率σ与电导率ρ成反比例,有公式可得σ为:bdV L I bdR L S 01===ρσ (12)又由μ、n 和σ的关系:σσH R nq u == (13)3. 误差分析霍尔效应产生的过程中会伴随有很多的其他效应,只有在理想过程中才能用我们前面的理论求出结果,实际过程要复杂的多,伴随有多种副效应,主要有四种。
3.1主要误差及原因(1)埃廷斯豪森效应当霍尔元件通以x 方向的电流,在与之垂直的z 方向再加上磁场,由于霍尔元件内部服从统计分布的载流子,速度不一,在磁场的作用下,速率快的载流子与速率快的载流子将在洛伦磁力和霍尔电场的共同作用下,沿y 轴向相反的两侧偏转。
载流子间相互碰撞将其动能转化成热能,速度快的一侧温度高,速度慢的一侧温度低,从而形成两边的温度差)(B A T T -。
因为霍尔电极和霍尔元件两侧材料各异,电极和元件就形成温差电偶,在A 、B 间产生温差电势差E U :IB U E ∝我们把这种效应称埃廷斯豪森效应。
(2)能特斯效应因为霍尔元件和电极的接触电阻不同,所以霍尔元件中在电极两边的电流,产生的焦耳热亦也不同,势引起两极间的温差电动,继而产生的电流叫温差电流此电动势又有产生温差电流(称为热电流)Q ,经过磁场的作用,电流偏离原来方向,最终在Y 方向上产生附加的电势差N U ,且 z N B x T U ∂∂∝这一效应称为能特斯效应。