下载文档原格式
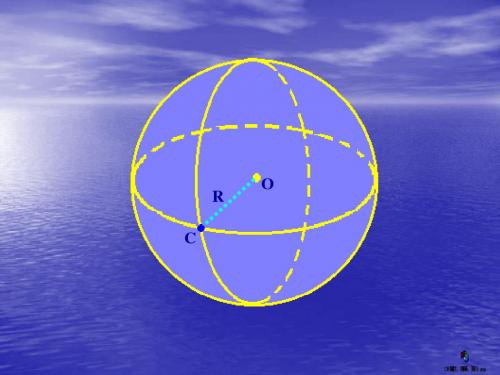
球的主要性质性质1. 球的任意一个截面都是圆。
其中过球心的截面叫做球的大圆,其余的截面 都叫做球的小圆。
已知球O 的半径为R 。
(1）若截面经过球心O .如图1，设A 是截面与球面的任意一个交点，连接OA 。
由球的定义可知,OA R =，所以点A 的轨迹是以O 为圆心，R 为半径的圆,即该截面是圆。
(2)若截面不经过球心O .如图1，设球心O 在截面上的射影为1O ，B 是截面与球面的任意一个交点，连接1OO ， OB 和1O B ,则OB R =为定值,且1OO 也为定值，所以2211O B R OO =-为定值，因此，点B 的轨迹是以1O 为圆心，1O B 为半径的圆，即该截面也是圆。
性质2. 球的小圆的圆心和球心的连线垂直于小圆所在的平面。
反之，球心在球的小圆所在平面上的射影是小圆的圆心。
如图2所示，若圆1O 是球O 的小圆,则11OO O ⊥圆面。
证明：如图,设AB ，CD 分别是圆1O 的两条直径，连接OA ,OB ，OC ,OD ,1OO .依题意可得OA OB =,所以1OO AB ⊥。
同理可得1OO CD ⊥，又因为1AB CD O =，所以11OO O ⊥圆面.性质3。
如图2，设球O 的半径为R ，球O 的小圆的圆心为1O ,半径为r ,球心O 到小圆1O 的距离1OO d =,则由性质2得22d R r =-，或22r R d =-。
性质4。
球的两个平行截面的圆心的连线垂直于这两个截面，且经过球心. 如图3,设球O 的两个平行截面的圆心分别为1O ，2O ，连接1OO ，2OO ,由性质3可知，11OO O ⊥圆面，又因为12//O O 圆面圆面，所以12OO O ⊥圆面.同理可得，21OO O ⊥圆面，且22OO O ⊥圆面,所以O ,1O ，2O 三点共线，因此，12O O 垂直于1O 圆面和2O 圆面,且12O O O ∈。
性质5. 球的直径等于球的内接长方体的对角线长.性质6. 若直棱柱的所有顶点都在同一个球面上,则该球的球心O 是直棱柱的两 个底面的外接圆的圆心的连线的中点.例1.(10年·第10题)设三棱柱的侧棱垂直于底面，所有棱长都为a ,顶点都在一 个球面上，则该球的表面积为( )(A)2a π (B)273a π （C)2113a π (D)25a π 解：如图，设球心为O ，半径为R ，底面△ABC 的中心为E ，连接OC ,OE 和CE 。
