基础沉降计算6页word

6.3 常用的地基沉降计算方法这里所讲的地基沉降量是指地基最终沉降量，目前常用的计算方法有：弹性力学法、分层总和法、应力面积法和考虑应力历史影响的沉降计算法。

所谓最终沉降量是地基在荷载作用下沉降完全稳定后的沉降量，要达到这一沉降量的时间取决于地基排水条件。

对于砂土，施工结束后就可以完成；对于粘性土，少则几年，多则十几年、几十年乃至更长时间。

6.3.1 计算地基最终沉降量的弹性力学方法地基最终沉降量的弹性力学计算方法是以Boussinesq 课题的位移解为依据的。

在弹性半空间表面作用着一个竖向集中力P 时，见图6-5，表面位移w (x, y, o )就是地基表面的沉降量s ：E r P s 21μπ-⋅= （6-8）式中 μ—地基土的泊松比；E —地基土的弹性模量（或变形模量E 0）；r —为地基表面任意点到集中力P 作用点的距离，22y x r +=。

对于局部荷载下的地基沉降，则可利用上式，根据叠加原理求得。

如图6-6所示，设荷载面积A 内N （ξ，η）点处的分布荷载为p 0（ξ，η），则该点微面积上的分布荷载可为集中力P= p 0（ξ，η）d ξd η代替。

于是，地面上与N 点距离r =22)()(ηξ-+-y x 的M （x, y ）点的沉降s （x, y ），可由式（6-8）积分求得：⎰⎰-+--=Ay x d d p E y x s 22002)()(),(1),(ηξηξηξμ （6-9）从式（6-9）可以看出，如果知道了应力分布就可以求得沉降；反过来，若沉降已知又图6-5 集中力作用下地基表面的沉降曲线图6-6 局部荷载下的地面沉降（a ）任意荷载面；（b ）矩形荷载面可以反算出应力分布。

对均布矩形荷载p 0（ξ，η）= p 0=常数，其角点C 的沉降按上式积分的结果为：021bp E s c ωμ-= （6-10）式中 c ω—角点沉降影响系数，由下式确定：⎪⎪⎭⎫ ⎝⎛+++++=)1ln()11ln(122m m mm m c πω （6-11）式中 m=l/b 。

1．某正常固结土层厚2.0m ，其下为不可压缩层，平均自重应力100cz a p kP =；压缩试验数据见表，建筑物平均附加应力0200a p kP =，求该土层最终沉降量。

【解】土层厚度为2.0m ，其下为不可压缩层，当土层厚度H 小于基础宽度b 的1/2时，由于基础底面和不可压缩层顶面的摩阻力对土层的限制作用，土层压缩时只出现很少的侧向变形，因而认为它和固结仪中土样的受力和变形很相似，其沉降量可用下式计算：1211e e s H e -=+ 式中，H ——土层厚度；1e ——土层顶、底处自重应力平均值c σ，即原始压应力1c p σ=，从e p-曲线上得到的孔隙比e ；2e ——土层顶、底处自重应力平均值c σ与附加应力平均值z σ之和2c z p σσ=+，从e p -曲线上得到的孔隙比e ；1100c a p kP σ==时，10.828e =；2100200300c z a p kP σσ=+=+=时，20.710e = 1210.8280.7102000129.1110.828e e s H mm e --==⨯=++2．超固结黏土层厚度为4.0m ，前期固结压力400c a p kP =，压缩指数0.3c C =，再压缩曲线上回弹指数0.1e C =，平均自重压力200cz a p kP =，天然孔隙比00.8e =，建筑物平均附加应力在该土层中为0300a p kP =，求该土层最终沉降量。

【解】超固结土的沉降计算公式为：当c cz p p p ∆>-时（300400200200a c cz a p kP p p kP ∆=>-=-=）时，10lg lg 1ni ci li i cn ei cii ili ci H p p p s C C e p p =⎡⎤⎛⎫⎛⎫+∆=+⎢⎥ ⎪ ⎪+⎝⎭⎝⎭⎣⎦∑式中，i H ——第i 层土的厚度；0i e ——第i 层土的初始孔隙比；ei C 、ci C ——第i 层土的回弹指数和压缩指数； ci p ——第i 层土的先期固结压力；li p ——第i 层土自重应力平均值，()12c i li ci p σσ-⎡⎤=+⎣⎦；i p ∆——第i 层土附加应力平均值，有效应力增量()12z i i zi p σσ-⎡⎤∆=+⎣⎦。

基础沉降算例基础资料和地质资料如上图。

计算依据规范为《公路桥涵地基与基础设计规范》JTG D63——2007（以下简称规范）。

TB100002.5—2005h p p γ-=0 《规范》4.3.4 （3.2.2）=157-17*1.87=125.21kPa56.15.4/02.7/(/==基础短边）基础长边b l第一层土：13.29613.98010=-==z z47.05.4/13.2//==基础短边）（土层底距基底距离b z938.0110==αα第二层土：13.79113.9813.221=-==z z58.15.4/13.7/==b z600.0938.021==αα第三层土：13.128613.9813.732=-==z z70.25.4/13.12/==b z412.0600.032==αα第四层土：13.158313.9813.1243=-==z z 36.35.4/13.15/==b z346.0412.043==αα第五层土：13.207813.9813.1514=-==z z47.45.4/13.20/==b z272.0346.054==αα 以上n α根据b l /及b z /可查询《规范》附录M 桥涵基底附加系数α、平均附加系数α，（附录B ）也可按本算例提供的Excel 表查询。

按《规范》4.3.7估算n z )ln 4.05.2(b b z n -=54.8)5.4ln 4.05.2(5.4=-⨯=m所以计算时取至基底下第三层土。

按《规范》4.3.4 （3.2.2）)(11100--=-=∑i i i i n i si z z E p s αα =125.21*[(2.13*0.938-0*1)/10+(7.13*0.600-2.13*0.938)/12+(12.13*0.412-7.13*0.600)/28]=52.02（mm ）查《规范》表4.3.6 Δz 值 （表3.2.2—1）Δz=0.8m 33.118.013.12'2=-=z 52.25.4/33.11/==b z435.0'2=α28/)435.033.11412.013.12(21.125⨯-⨯⨯=∆n s )(3.1025.002.52)(31.0mm mm =⨯<=故以上取基底以下三层计算满足规范要求。

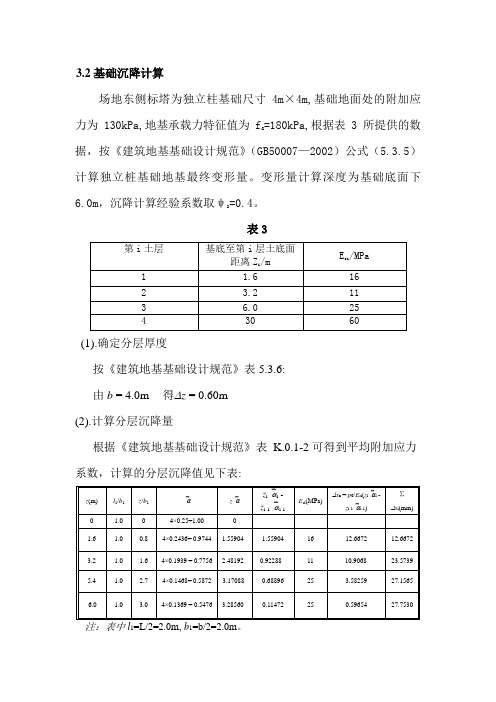
3.2基础沉降计算
场地东侧标塔为独立柱基础尺寸4m×4m,基础地面处的附加应力为130kPa,地基承载力特征值为f a=180kPa,根据表3所提供的数据，按《建筑地基基础设计规范》（GB50007—2002）公式（5.3.5）计算独立桩基础地基最终变形量。

变形量计算深度为基础底面下6.0m，沉降计算经验系数取ψs=0.4。

表3
(1).确定分层厚度
按《建筑地基基础设计规范》表5.3.6:
由b = 4.0m 得∆z = 0.60m
(2).计算分层沉降量
根据《建筑地基基础设计规范》表K.0.1-2可得到平均附加应力系数，计算的分层沉降值见下表:
11
在z = 6.0m范围内的计算沉降量∑∆s =27.753mm, z = 5.4m至6.0m(∆z为0.60m)
土层计算沉降量∆s'n= 0.59654 mm≤0.025∑∆s'i = 0.025 ×27.7530= 0.6938mm。

满足要求
（3）最终的沉降量
s = ψs s' = ψs∑∆s'i = 0.4× 27.7530= 11.101mm。

1．某正常固结土层厚2.0m ，其下为不可压缩层，平均自重应力100cz a p kP =；压缩试验数据见表，建筑物平均附加应力0200a p kP =，求该土层最终沉降量。

【解】土层厚度为2.0m ，其下为不可压缩层，当土层厚度H 小于基础宽度b 的1/2时，由于基础底面和不可压缩层顶面的摩阻力对土层的限制作用，土层压缩时只出现很少的侧向变形，因而认为它和固结仪中土样的受力和变形很相似，其沉降量可用下式计算：1211e e s H e -=+ 式中，H ——土层厚度；1e ——土层顶、底处自重应力平均值c σ，即原始压应力1c p σ=，从e p-曲线上得到的孔隙比e ；2e ——土层顶、底处自重应力平均值c σ与附加应力平均值z σ之和2c z p σσ=+，从e p -曲线上得到的孔隙比e ；1100c a p kP σ==时，10.828e =；2100200300c z a p kP σσ=+=+=时，20.710e = 1210.8280.7102000129.1110.828e e s H mm e --==⨯=++2．超固结黏土层厚度为4.0m ，前期固结压力400c a p kP =，压缩指数0.3c C =，再压缩曲线上回弹指数0.1e C =，平均自重压力200cz a p kP =，天然孔隙比00.8e =，建筑物平均附加应力在该土层中为0300a p kP =，求该土层最终沉降量。

【解】超固结土的沉降计算公式为：当c cz p p p ∆>-时（300400200200a c cz a p kP p p kP ∆=>-=-=）时，10lg lg 1ni ci li i cn ei cii ili ci H p p p s C C e p p =⎡⎤⎛⎫⎛⎫+∆=+⎢⎥ ⎪ ⎪+⎝⎭⎝⎭⎣⎦∑式中，i H ——第i 层土的厚度；0i e ——第i 层土的初始孔隙比；ei C 、ci C ——第i 层土的回弹指数和压缩指数； ci p ——第i 层土的先期固结压力；li p ——第i 层土自重应力平均值，()12c i li ci p σσ-⎡⎤=+⎣⎦；i p ∆——第i 层土附加应力平均值，有效应力增量()12z i i zi p σσ-⎡⎤∆=+⎣⎦。

基础沉降计算范文基础沉降是指土壤或岩石在受力作用下发生形变，导致地表或建筑物下沉的现象。

它是建筑工程中非常重要的一个参数，对于确保建筑物的稳定性和使用安全至关重要。

本文将介绍基础沉降的计算方法。

基础沉降的计算主要分为两个部分：土壤的压缩性计算和基础的沉降计算。

首先是土壤的压缩性计算。

土壤的压缩性是指土壤在加荷时体积变化的能力。

根据土壤的压缩性特征，一般可以将土壤分为粘性土和砂性土两种类型。

对于粘性土来说，其压缩性主要表现为固结。

固结是指由于增加外界的应力，土壤颗粒间的空隙被压缩，导致土壤体积减小的过程。

固结性压缩量可以通过振实度指数来计算，具体计算公式如下：Sc = Hc * log(Po/Pc)其中，Sc是固结性压缩量，Hc是土壤的压缩指数，Po是初始应力，Pc是最终应力。

对于砂性土来说，其压缩性主要表现为沉降。

沉降是指土壤受到荷载作用后，土壤颗粒重新排列，导致土壤体积减小的过程。

沉降性压缩量可以通过沉降模量来计算，具体计算公式如下：Sc = 1/E0 * log(Po/Pc)其中，Sc是沉降性压缩量，E0是沉降模量，Po是初始应力，Pc是最终应力。

接下来是基础的沉降计算。

基础的沉降主要分为弹性沉降和剪切沉降两部分。

弹性沉降是指由于土体的弹性变形而产生的沉降。

弹性沉降的计算方法有很多种，最常用的一种方法是采用弹性沉降系数法，即根据沉降观测的结果，通过实测值和经验公式进行计算。

公式如下：Sd=C*q*B其中，Sd是基础的弹性沉降，C是弹性沉降系数，q是基础承受的荷载，B是基础的面积。

剪切沉降是指由于土体的刚性变形而产生的沉降。

剪切沉降的计算方法一般采用承载力沉降法，即根据土体的刚性变形特性，通过基础的承载力计算得出沉降值。

具体计算公式如下：Sd=(q/Nk)*B其中，Sd是基础的剪切沉降，q是基础承受的荷载，Nk是土体的承载力系数，B是基础的面积。

需要注意的是，以上的计算公式只是基础沉降计算中的一部分，实际的计算过程可能更加复杂。

&2垂直荷载地基应力σp(一)计算图式如图[1]1.空心桩外荷载P=40547（KN ）i.50m T 梁支座反力 P 1=36960（KN ） ii.长16.60m 冒 梁 P 2=2291 （KN ） iii. φ2.30m 双桥墩柱 P 3=1296 （KN ）2.空心桩自重G 桩=31490（KN ）G 1=15 4×2=308×[25KN/方]=7700（KN ）G 2=6 8 ×2=136×[25KN/方]=3400（KN ）G 3=62.7×4=250×[25KN/方]=6270（KN ）G 4=50.1×4=200×[25KN/方]=5000（KN ）G 5=9 5 ×4=380×[24KN/方]=9120（KN ）3.桩底垂直荷载（恒载）总和∑G 0=P+G=40547+31490=72037（KN ）(二)按土壤扩散角计算桩底应力1.如图4-2 土坡扩散角θ=4ϕ=154︒=3.75° 桩长16m 扩散角锥体底面直径如下：D=d+h ·tan θ=11+(16×0.0655) ×2=11+(1.05×2=2.10)=16.10（m ）A D =16.102×4π =204(m 2)2.地层不同深度的允许应力(JTGD63-2007)[f a ]=[ f a 0]+k 1r 1(b-2)+ k 2r 2(h-3) --(3.3.4)粉粘土承载力基本容许值[ f a 0]=0.20（MPa ）=200(KN/m 2)宽度修正系数k 1=0 深度修正系数k 2=1.5基底埋置深度h=16（m ）[ f a h ]=0.200+1.5×1.97×(16-3)=0.200+0.38=0.58（MPa ）=580（KN/m 2）3.挖孔桩外形体积∑V g =1957(方)V 1=φ1 4 ×2=154×2=308（方）V 2=φ13.5×2=143×2=286（方）V 3=φ1 3 ×4=133×4=531（方）V 4=φ1 2 ×4=113×4=452（方）V 5=φ1 1 ×4=9 5×4=380（方）4.桩长h=16m 中锥体体积V 0=141615420416286422φφ++=⨯=（方）土的体积V 土= V 0-V g =2864-1957=907(方)土重G 土=907 ×[19.7t/方]=17868(KN)5.桩端水平线上桩自重，垂直重量在直线D=16.10（m ）中的应力∑Q g =G 桩+ G 土=31490+17868=49358(KN)应力σg =gDQA ∑=49358204=242(KN/m 2)6.考虑桥墩及上部构造恒载后应力∑Q p = ∑Q g + P=49358+40547=89905(KN)σp = p D Q A ∑= 89905204=441(KN/m 2) ＜[580 KN/m 2]故安全。

基础沉降量计算
由于地质报告未给出③残积土、④1全风化层、④2中风化层压缩模量Es，故以下根据《高层建筑岩土工程勘察规程》JGJ 72-2004 附录B 采用变形模量E0估算天然地基的平均沉降量。

公式:
地基沉降计算深度可按下式计算：
查地质报告，取离酒店筏板基础相邻的钻孔ZK34处的ZJ3进行沉降复核(该独立基础尺寸为6.1x6.1m)。

基础底持力层为③残积
土，基础底标高为20.60(绝对标高)，基础底至该层土层底厚度为5.14 米，变形模量E0=42Mpa。

其下一层为④2全风化层，土层厚度为13.5米,变形模量E0=149Mpa。

地基沉降计算深度为：Zn=b(2.5-0.4ln3.5)= 12.2米。

地基承载力特征值取值为200Kpa。

地基沉降量为：
=1.5*200* *6.10*0.75*(0.7332-0.3932)/149
= 3.132mm
沉降量较小。

另外，筏板在ZK34附近的沉降量最大值为4mm（见筏板沉降量计算书）
由此，ZK34处独立基础跟筏板的沉降差Δs=S2-S1= 0.87mm。

小于0.002L。

经计算，基础沉降量及沉降差均在规范许可范围内。

基础沉降计算本工程多数单体为多层（6层）住宅，个别为小高层（9层）住宅；另外，7#、8#楼为商业配套（3层）。

其中多层住宅和商业配套楼采用砖混结构，基础为条形基础。

根据地质勘察报告，基础持力层一般为粘质粉土、砂质粉土②层或粉质粘土、粘质粉土②1层，承载力标准值fka=160Kpa。

地基变形允许值按《北京地区建筑地基基础勘察设计规范》（DBJ 01-501-92），取30mm。

以下按三种埋深控制基础附加应力p0值。

一、基础埋深1.5米基底以上平均土容重r=18KN/M2。

S=ΨS *S C=ΨS*Σ*P O/Esi*(Zi*αi- Z i-1*αi-1)P O<S / Σ1/Esi*(Zi*αi- Z i-1*αi-1)=30/0.7*[0.85*2.5/18.1+(0.736*4-0.85*2.5)/8.4+(0.64*5.3-0.736*4)/18.7+(0.553*7.3-0.64*5.3)/7.8+(0.51*8.3-0.553*7.3)/25]= 30/0.7[0.117+0.098+0.024+0.083+0.008]=129.8Kpa.二、基础埋深2.0米基底以上平均土容重r=18KN/M2。

S=ΨS *S C=ΨS*Σ*P O/Esi*(Zi*αi- Z i-1*αi-1)P O<S / Σ1/Esi*(Zi*αi- Z i-1*αi-1)=30/0.7*[0.89*2.0/18.1+(0.757*3.5-0.89*2.0)/8.4+(0.673*4.8-0.757*3.5)/18.7+(0.56*6.8-0.673*4.8)/7.8 +(0.53*7.8-0.56*6.8)/25]= 30/0.7[0.098+0.104+0.031+0.074+0.013]=134Kpa.三、基础埋深3.0米基底以上平均土容重r=18KN/M2。

S=ΨS *S C=ΨS*Σ*P O/Esi*(Zi*αi- Z i-1*αi-1)P O<S / Σ1/Esi*(Zi*αi- Z i-1*αi-1)=30/0.7*[0.97*1.0/18.1+(0.86*2.5-0.97*1.0)/8.4+(0.74*3.8-0.86*2.5)/18.7+(0.61*5.8-0.74*3.8)/7.8+(0.57*6.8-0.61*5.8)/25]= 30/0.7[0.054+0.140+0.035+0.093+0.014]=127.6K pa.结论：根据地勘报告，地基承载力标准值fak=160Kpa，但为了控制沉降量不大于30mm，条基均反力按120 Kpa计，由此计算条形基础宽度。

基础最终沉降量的计算一、基础最终沉降量的计算方法1.1弹性计算法弹性计算法是根据土壤力学、弹性力学等基本原理，考虑土壤-结构相对位移引起的沉降，采用数值计算方法进行分析。

该方法需要建立基础-土壤-结构的有限元模型，通过求解方程组得到基础的沉降量。

1.2半经验计算法半经验计算法结合了实测数据和经验公式，通过回归分析建立了合理的计算模型。

该方法根据不同地区的实测资料，结合土壤类型、地下水位、基础形式等因素，选择合适的经验公式进行计算。

1.3经验公式法经验公式法是基于大量实测数据和统计分析得出的计算公式，是一种简便快速的计算方法。

该方法根据土壤类型、荷载大小、基础形式等因素，选择合适的公式计算基础的最终沉降量。

二、影响基础最终沉降量的因素2.1土壤性质不同土壤具有不同的压缩性和可变性，影响基础沉降的速度和程度。

一般来说，黏性土壤和可压缩土壤的基础沉降较大，而砂土和砾石的沉降较小。

2.2基础形式基础形式也是影响基础沉降的重要因素。

一般而言，承台式基础比单孔基础的基础沉降较大，而沉井式基础的沉降量较小。

2.3荷载大小荷载大小是影响基础最终沉降量的重要因素之一、荷载越大，基础的沉降量也越大。

2.4地下水位地下水位的高低对基础沉降有很大影响。

地下水位高的情况下，土壤饱和度增大，土壤的压缩性降低，基础的沉降量也相应减小。

三、基础最终沉降量的调整措施在基础最终沉降量计算的基础上，需要采取一定的调整措施来保证建筑物的稳定性。

3.1控制沉降速率基础沉降是一个时间过程，需要控制沉降速率，以避免建筑物的过大沉降。

可以通过增加基础面积、减小设计荷载等方式来控制沉降速率。

3.2选择合适的基础形式选择合适的基础形式也是一种调整措施。

对于沉降对建筑物稳定性要求较高的情况，可以选择较稳定的基础形式，如桩基础或沉井式基础。

3.3排水措施对于高地下水位和易液化土壤区域，需要采取适当的排水措施，降低土壤饱和度，减少基础沉降量。

3.4桩基础加固在地质条件较差的区域，可以考虑采用桩基础来加固，以减小基础的沉降量。