积和商的变化规律练习题

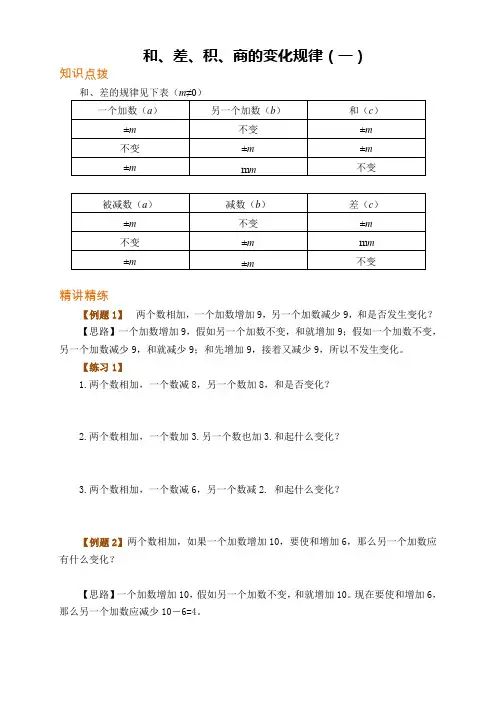
和、差、积、商的变化规律（一）知识点拨和、差的规律见下表（m≠0）精讲精练【例题1】两个数相加，一个加数增加9，另一个加数减少9，和是否发生变化？【思路】一个加数增加9，假如另一个加数不变，和就增加9；假如一个加数不变，另一个加数减少9，和就减少9；和先增加9，接着又减少9，所以不发生变化。

【练习1】1.两个数相加，一个数减8，另一个数加8，和是否变化？2.两个数相加，一个数加3.另一个数也加3.和起什么变化？3.两个数相加，一个数减6，另一个数减2. 和起什么变化？【例题2】两个数相加，如果一个加数增加10，要使和增加6，那么另一个加数应有什么变化？【思路】一个加数增加10，假如另一个加数不变，和就增加10。

现在要使和增加6，那么另一个加数应减少10－6=4。

【练习2】1.两个数相加，如果一个加数增加8，要使和增加15，另一个加数应有什么变化？2.两个数相加，如果一个加数增加8，要使和减少15，另一个加数应有什么变化？3.两个数相加，如果一个加数减少8，要使和减少8，另一个加数应有什么变化？【例题3】两数相减，如果被减数增加8，减数也增加8，差是否起变化？【思路】被减数增加8，假如减数不变，差就增加8；假如被减数不变，减数增加8，差就减少8。

两个数的差先增加8，接着又减少8，所以不起什么变化。

【练习3】1.两数相减，被减数减少6，减数也减少6，差是否起变化？2.两数相减，被减数增加12.减数减少12.差起什么变化？3.两数相减，被减数减少10，减数增加10，差起什么变化？【例题4】两数相乘，如果一个因数扩大8倍，另一个因数缩小2倍，积将有什么变化？【思路】如果一个因数扩大8倍，另一个因数不变，积将扩大8倍；如果一个因数不变，另一个因数缩小2倍，积将缩小2倍。

积先扩大8倍又缩小2倍，因此，积扩大了8÷2=4倍。

【练习4】1.两数相乘，如果一个因数缩小4倍，另一个因数扩大4倍，和是否起变化？2.两数相乘，如果一个因数扩大3倍，另一个因数缩小12倍，积将有什么变化？3.两数相乘，如果一个因数扩大3倍，另一个因数扩大6倍，积将有什么变化？【例题5】两数相除，如果被除数扩大4倍，除数缩小2倍，商将怎样变化？【思路】如果被除数扩大4倍，除数不变，商就扩大4倍；如果被除数不变，除数缩小2倍，商就扩大2倍。

积的变化规律练习题一、根据已知算式,直接写出下面各题的得数.18×24=432 105×45=4725（18÷2）×(24×2）= (105÷5)×（45×5）=（18×2）×（24÷2)= （105×3）×（45÷3）= 24×75＝1800 36×104＝3744（24○6）×（75×6)＝1800 （36×4）×（104○4）＝3744(24○3)×(75○□）＝1800 (36○□）×（104○□）＝374415×24=36015×72=( )30×24=（） 5×24=（ ) 15×12=( ）15×（24×）=3600 15×（24÷10）=（）12×20=240（12×6)×（20×5）=（ ) （12÷3）×（20÷4)=（）（12×）×（20×）=4800 （12÷）×（20÷）=40二、选择。

1．一个因数扩大5倍，另一个因数不变，积（）。

A、缩小5倍B、不变C、扩大5倍2．一个因数扩大5倍，另一个因数缩小5倍，积（）。

A、缩小5倍 B、不变 C、扩大5倍3．两数相乘，一个因数扩大2倍，另一个因数扩大3倍，那么积（）。

A、不变B、扩大5倍C、扩大6倍4．两个因数的积是60，这时一个因数缩小4倍，另一个因数不变,现在的积是( )A、240B、60C、155．一个长方形的面积为12平方米、把长扩大到原来的3倍，宽不变,扩大后的面积是（ )6．两个因数的积是100，把其中一个因数扩大到原来的3倍,另一个因数不变，积是（）7．一个正方形的面积为12平方米、把边长扩大到原来的3倍，，扩大后的面积是（ )8．两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数也扩大到原来的3倍,积是（）9．两个因数的积是100，把其中一个因数扩大到原来的3倍,另一个因数也缩小到原来的3倍，积是（）10．一个因数不变,把其中另一个因数扩大到原来的3倍，积是90，原来两个因数的积是( )11．一个因数扩大到原来的3倍，另一个因数也扩大到原来的3倍,积是90，原来两个因数的积是（）12．一个因数扩大到原来的3倍，另一个因数缩小到原来的3倍，积是90,原来两个因数的积是（）。

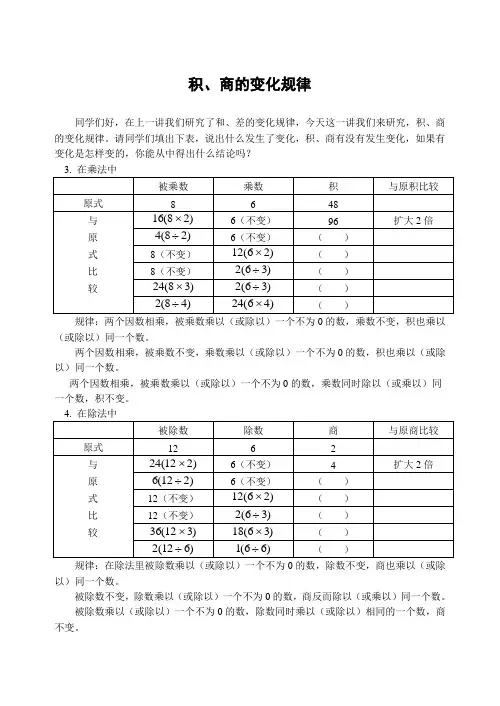
积、商的变化规律同学们好，在上一讲我们研究了和、差的变化规律，今天这一讲我们来研究，积、商的变化规律。

请同学们填出下表，说出什么发生了变化，积、商有没有发生变化，如果有变化是怎样变的，你能从中得出什么结论吗？规律：两个因数相乘，被乘数乘以（或除以）一个不为0的数，乘数不变，积也乘以（或除以）同一个数。

两个因数相乘，被乘数不变，乘数乘以（或除以）一个不为0的数，积也乘以（或除以）同一个数。

两个因数相乘，被乘数乘以（或除以）一个不为0的数，乘数同时除以（或乘以）同一个数，积不变。

规律：在除法里被除数乘以（或除以）一个不为0的数，除数不变，商也乘以（或除以）同一个数。

被除数不变，除数乘以（或除以）一个不为0的数，商反而除以（或乘以）同一个数。

被除数乘以（或除以）一个不为0的数，除数同时乘以（或除以）相同的一个数，商不变。

例1. 2584⨯=⨯⨯÷=⨯=()()254844100212100分析与解答：根据积的变化规律，一个因数扩大多少倍，另一个因数反而缩小相同的倍数，积不变的规律，使25×4，使84÷4，转化为100×21，这就很快计算出结果是2100。

例2. 12588⨯=⨯⨯÷=⨯=()()125888810001111000例3. 2250125÷=⨯÷⨯=÷=()()22508125818000100018分析与解答：根据商的变化规律，被除数和除数同时乘以或除以一个数（不为0）商不变的规律，可以使2250×8，使125×8，转化为18000÷1000，这样就能很快算出结果是18。

【模拟试题】（答题时间：45分钟）（一）尝试体验 1. 填一填1272244⨯⨯⨯⨯⨯⎫⎬⎪⎪⎪⎭⎪⎪⎪=÷÷÷÷÷⎫⎬⎪⎪⎪⎭⎪⎪⎪=()()()()()()()()()()()()()()()()()() 完成上面两组题后，每组后面的4个题与第一算式比较各部分是怎样变化的，才保证了使它们的和、差、积、商没发生变化？ 2. 利用积、商变化规律，计算下面各题。

四年级数学上册积和商的变化规律练习题Prepared on 21 November 2021第16周周练积的变化规律一、填空题。

1.写得数并发现规律。

16×17=32×17=16×34=48×17=16×51=64×17=我发现了：一个因数相同，另一个因数（），积也（）。

请在上面的横线上举一个例子验证你的发现。

20×18=20×18=10×18=20×9=5×18=20×3=我发现了：一个因数相同，另一个因数（），积也（）。

请在上面的横线上举一个例子验证你的发现。

2.根据以上的发现填空。

（1）42×56=235242×112=（）21×56=（）42×28=（）7×56=（）（2）5×14=705×28=（）5×42=（）5×56=（）5×70=（）3.一个因数不变，另一个因数乘几或除以几（0除外），积也（）。

4.两个因数的积是360，如果一个因数除以3，另一个因数不变，积变为（）。

5.两个因数相乘，一个因数乘6，另一个因数不变，那么积（）。

6.两个因数相乘的积是5600，如果一个因数不变，另外一个因数除以10，那么积是（）。

7.两个数相乘是75，如果一个因数乘7，另一个因数除以7，积是（）。

8.已知A×B=400，如果A乘3，则积是（），如果B除以5，则积是（）。

9.两数相乘，如果一个因数缩小5倍，另一个因数扩大5倍，积()。

10.两数相乘，如果一个因数扩大8倍，另一个因数缩小2倍，积()。

11.两个数相乘，一个因数乘10，另一个因数也乘10，积（）。

12.两个因数的积是420，如果一个因数不变，另一个因数乘8，积是（）。

13.两个数相乘的积是160，如果一个因数除以2，另一个因数也除以2，积是（）。

积和商“变与不变”规律㈠、积的变化规律：⑴、一个因数不变，另一个因数乘（或除以）几，积就相应的乘（或除以）几。

字母表示：如果a×b=c ，则(a×3)×b=c×3举例：a×b=12 如果(a×3)则积就是12×3=36.⑵、一个数乘一个比1大的数，积比原数大；⑶、一个数乘一个比1小的数，积比原数小。

㈡、积不变规律：一个因数乘（或除以）几，另一个因数相应的除以(或乘)几，积不变。

字母表示：如果a×b=c 则（a×5）×（b÷5）=c㈢、商的变化规律：⑴被除数不变，除数乘或除以几，商就相应的除以或乘几。

字母表示：如果a÷b=c ，则a÷（b×3）=c÷3本文档下载后根据实际情况可编辑修改使用举例：a÷b=12 如果(b×3)则商就是12÷3=4⑵除数不变，被除数乘或除以几，商就相应的乘或除以几。

字母表示：如果a÷b=c ，则(a×3)÷b=c×3举例：a÷b=12 如果(a×3)则商就是12×3=36.被除数大于除数，商就大于1；被除数小于除数，商就小于1.一个数除以一个比1大的数，商比被除数要小；一个数除以一个比1小的数，商比被除数要大。

㈣、商不变规律：被除数和除数同时乘或除以几，商不变。

1、根据78×12＝936，填写下面各题的结果。

7.8×12＝（） 0.78×12＝（） 7.8×0.12＝（） 0.78×（）＝936本文档下载后根据实际情况可编辑修改使用2、根据414÷18＝23，填写下面各题的结果。

4.14÷1.8＝（） 4140÷1.8＝（） 0.414÷0.18＝（） 41.4÷18＝（）3、根据45×63＝2835，填写下面各题的结果。

积和商的变化规律1、发现规律直接写得数。

16×17=272 32×17= 32×34=16×34= 48×17= 8×34=16×51= 64×17= 4×68=2、发现规律直接写得数。

2000÷25=80（2000×2）÷（25×2）= （2000×15）÷（25×15）=（2000÷5）÷（25÷5）= （2000÷18）÷（25÷18）=（2000÷5）÷25= （2000×20）÷25=2000÷（25÷5）= 2000÷（25×5）=（2000÷5）÷（25×2）= （2000×5）÷（25÷2）=（2000÷2）÷（25÷4）= （2000×2）÷（25×8）=3、两个因数的积是360，如果一个因数除以3，另一个因数不变，积变为（）。

4、两个因数相乘，一个因数乘6，另一个因数不变，那么积（）。

5、两个因数相乘的积是5600，如果一个因数不变，另外一个因数除以10，那么积是（）。

6、两个数相乘是75，如果一个因数乘7，另一个因数除以7，积是（）。

7、已知A×B=400，如果A乘3，则积是（），如果B除以5，则积是（）。

8、两个数相乘，一个因数乘10，另一个因数也乘10，积（）。

9、两个因数的积是420，如果一个因数不变，另一个因数乘8，积是（）。

10、两个数相乘的积是160，如果一个因数除以2，另一个因数也除以2，积是（）。

11、两数相除的商是15，如果被除数、除数同时扩大10倍，商是（）。

第16周周练积的变化规律一、填空题。

1.写得数并发现规律。

16×17= 32×17=16×34= 48×17=16×51= 64×17=我发现了：一个因数相同，另一个因数（），积也（）。

请在上面的横线上举一个例子验证你的发现。

20×18= 20×18=10×18= 20×9=5×18= 20×3 =我发现了：一个因数相同，另一个因数（），积也（）。

请在上面的横线上举一个例子验证你的发现。

2.根据以上的发现填空。

（1）42×56=2352 42×112=（）21×56=（）42×28=（）7×56=（）（2）5×14=70 5×28=（）5×42=（）5×56=（）5×70=（）3.一个因数不变，另一个因数乘几或除以几（0除外），积也（）。

4.两个因数的积是360，如果一个因数除以3，另一个因数不变，积变为（）。

5.两个因数相乘，一个因数乘6，另一个因数不变，那么积（）。

6.两个因数相乘的积是5600，如果一个因数不变，另外一个因数除以10，那么积是（）。

7.两个数相乘是75，如果一个因数乘7，另一个因数除以7，积是（）。

8.已知A×B=400，如果A乘3，则积是（），如果B除以5，则积是（）。

9.两数相乘，如果一个因数缩小5倍，另一个因数扩大5倍，积( )。

10.两数相乘，如果一个因数扩大8倍，另一个因数缩小2倍，积( )。

11.两个数相乘，一个因数乘10，另一个因数也乘10，积（）。

12.两个因数的积是420，如果一个因数不变，另一个因数乘8，积是（）。

13.两个数相乘的积是160，如果一个因数除以2，另一个因数也除以2，积是（）。

14.芳芳在计算乘法时，把一个因数末尾多写了1个0，结果得到800，正确的积是应该是（）。

浙江省2022-2023学年期末试题汇编—09商的变化规律、积的变化规律（试题）-五年级上册数学人教版一．选择题（共4小题）1．（2022秋•上虞区期末）计算“7.65÷0.85”时，可以把除数转化成85，同时，把被除数扩大到原来的100倍。

这样算的依据是（ ）A．除法的性质B．小数的性质C．积不变规律D．商不变的性质2．（2022秋•瑞安市期末）下列算式中，与24×96结果不相等的是（ ）A．240×9.6B．2.4×960C．2.4×9.6D．（24×2）×（96÷2）3．（2022秋•平阳县期末）a÷0.8（a＞0）的商一定（ ）A．大于a B．小于a C．等于a D．无法确定4．（2022秋•慈溪市期末）下列算式中，如果△不为0，得数最大的是（ ）A．△÷1.5B．△÷0.5C．△×1.1D．△×0.9二．填空题（共10小题）5．（2022秋•上虞区期末）在横线里填上“＞”“＜”或“＝”。

（1）7 7.4（2）2.8÷1.5 2.8×1.5（3）2.4÷0.12 2.4÷1.2（4）3.72÷0.25 3.72×4 6．（2022秋•上虞区期末）根据214×46＝9844，可知2.14×4.6＝ ，984.4÷0.46＝ 。

7．（2022秋•嘉善县期末）根据78×25＝1950，直接写出下面算式的得数。

7.8×2.5＝ 19.5÷0.78＝ 1.95÷2.5＝ 8．（2022秋•奉化区期末）根据36×1.2＝43.2，直接写出下面各题的结果。

3.6×1.2＝ 360×0.12＝ 43.2÷3.6＝ 4.32÷0.12＝ 9．（2022秋•奉化区期末）比一比，在横线上填上“＞”、“＜”或“＝”。

一、积的变化规律1、一个因数不变，另一个因数乘几或除以几（0除外），积也乘几或除以几。

2、两个数相乘，一个因数乘或除以几（0除外），另一个因数除以或乘相同的数，则它们的乘积不变。

（1）42×5= （2）48×16=76842×15= （48×4）×（16÷4）=420×15= （48÷8）×（16×8）=840×15= （48×5）×（16○□）=768（3）7本作业本摞起来高25毫米，全班56本作业本摞起来有多高？（4）一个宽为9米的长方形菜地，面积是252平方米，如果把这块长方形菜地的宽增加到36米，长不变，扩建后的面积是多少？二、商的变化规律1、除数不变，被除数乘几或除以几（0除外），商也乘几或除以几。

2、被除数不变，除数乘几或除以几（0除外），商反而除以几或乘几。

3、被除数和除数都乘或除以一个相同的数（0除外），商不变。

（1）80÷16=（80○□）÷（16÷4）200÷40=（200÷20）÷（40○□）180÷15=（180×3）÷（15○□）（2）1400÷70，如果除数不变，被除数除以10，那么商应当（）。

被除数不变，除数乘3，商应当（）。

两个数的商是8，如果被除数不变，除数乘4，商就变成（）。

一个除法算式，被除数乘15，要使商不变，除数也要（）。

两个数相除的商是6，如果被除数和除数都除以12，商是（）。

一个除法算式的被除数、除数都除以3后，商是20，那么原来的商是（）。

.《除数是两位数的除法》1、商店里卖衣服，29元/件，49元/2件，王阿姨有185元，最多可以买多少件？还剩多少元？2、小李家距离学校520米，小李每分钟走65米，小红每分钟走60米，从家到学校小红比小李多走5分钟，小红家离学校多少米？3、每条裤子75元，商店推出优惠活动，买4条送一条，900元钱最多可以买几条这样的裤子？4、12箱蜜蜂一年可以酿900千克蜂蜜，林叔叔家养了8箱这样蜜蜂，一年可以酿多少千克蜂蜜？5、学校组织四年级的540名学生去植树，要分成9个植树点，每个植树点分成4个小组，平均每个小组有多少人？6、从山顶到山脚共998米，王林爬了14分钟，距山顶还有260米，他平均每分钟爬多少米？【下载本文档，可以自由复制内容或自由编辑修改内容，更多精彩文章，期待你的好评和关注，我将一如既. 往为您服务】。

命题人：葛金韬★观察下列三组算式，你发现了什么?从上面的算式中可以看出：(1)一个因数不变，另一个因数扩大到它的几倍，积也扩大相同的倍数；(2)如果两个因数都扩大，那么积就扩大两个因数扩大的倍数的乘积；(3)如果一个因数扩大，另一个因数缩小，那么积就扩大(或缩小)两个因数扩大或缩小倍数的商。

例题1在乘法算式25×8中，如果一个因数扩大到它的2倍，另一个因数不变，那么积有什么变化?例题2在乘法算式510×360中，如果一个因数扩大到它的2倍，另一个因数扩大到它的3倍，那么积有什么变化?例题3在乘法算式510×360中，如果一个因数扩大到它的6倍，另一个因数缩小到原来的三分之一，那么积有什么变化?例题4在乘法算式510×360中，如果一个因数扩大到它的2倍，另一个因数缩小到原来的六分之一，那么积有什么变化?练习1．填空在乘法算式中，一个因数不变，另一个因数扩大到它的2倍，积( )；一个因数不变，另一个因数缩小到原来的三分之一，积( )；一个因数扩大到它的4倍，另一个因数扩大到它的3倍，积( )；一个因数缩小到原来的二分之一，另一个因数扩大到它的8倍，积( )。

2．先判断，再计算验证(1)在算式12×8中，如果一个因数不变，另一个因数扩大到它的3倍，积有什么变化?(2)在算式12×8中，如果一个因数不变，另一个因数缩小到原来的四分之一，积有什么变化?(3)在算式12×8中，如果一个因数不变，另一个因数缩小到原来的三分之一，积有什么变化?(4)在算式12×8中，如果一个因数缩小到它的三分之一，另一个因数缩小到它的四分之一，积有什么变化?(5)在算式12×8中，如果一个因数扩大到它的3倍，另一个因数扩大到它的4倍，积有什么变化?命题人：葛金韬★观察下列三组算式，你发现了什么?从上面的算式可以看出：(1)除数不变，被除数扩大到它的几倍，商也扩大相同的倍数；(2)被除数不变，除数扩大到它的几倍，商就缩小到原来的几分之一；(2)如果被除数、除数都扩大，那么商就扩大(或缩小)被除数与除数扩大(或缩小)倍数的商倍；(3)如果被除数扩大，除数缩小，那么商就扩大被除数扩大倍数与除数缩小倍数的乘积倍；(4)如果被除数缩小，除数扩大，那么商就缩小被除数缩小与除数扩大倍数的乘积分之一。

积的变化规律练习题姓名一、根据已知算式，直接写出下面各题的得数。

18×24=432105×45=4725（18÷2）×（24×2）= （105÷5）×（45×5）=（18×2）×（24÷2）= （105×3）×（45÷3）=24×75＝180036×104＝3744（24○6）×（75×6）＝1800 （36×4）×（104○4）＝3744 （24○3）×（75○□）＝1800 （36○□）×（104○□）＝3744 15×24=36015×72=（）30×24=（）5×24=（）15×12=（）15×（24×）=3600 15×（24÷10）=（）12×20=240（12×6）×（20×5）=（）（12÷3）×（20÷4）=（）（12×）×（20×）=4800 （12÷）×（20÷）=40 二、选择。

1．一个因数扩大5倍，另一个因数不变，积（）。

A、缩小5倍B、不变C、扩大5倍2．一个因数扩大5倍，另一个因数缩小5倍，积（）。

A、缩小5倍B、不变C、扩大5倍3．两数相乘，一个因数扩大2倍，另一个因数扩大3倍，那么积（）。

A、不变B、扩大5倍C、扩大6倍4．两个因数的积是60，这时一个因数缩小4倍，另一个因数不变，现在的积是（）A、240 B、60 C、155．一个长方形的面积为12平方米、把长扩大到原来的3倍，宽不变，扩大后的面积是（）6．两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数不变，积是（）7．一个正方形的面积为12平方米、把边长扩大到原来的3倍，，扩大后的面积是（）8．两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数也扩大到原来的3倍，积是（）9．两个因数的积是100，把其中一个因数扩大到原来的3倍，另一个因数也缩小到原来的3倍，积是（）10．一个因数不变，把其中另一个因数扩大到原来的3倍，积是90，原来两个因数的积是（）11．一个因数扩大到原来的3倍，另一个因数也扩大到原来的3倍，积是90，原来两个因数的积是（）12．一个因数扩大到原来的3倍，另一个因数缩小到原来的3倍，积是90，原来两个因数的积是（）。

和.差,积、商的变化规律（一）知识点拨和、差的规律见下表（于0精讲精练【例题1】两个数相加，一个加数增加9,另一个加数减少9,和是否发生变化？【思路】一个加数增加9,假如另一个加数不变，和就增加9；假如一个加数不变，另一个加数减少9,和就减少9；和先增加9,接着又减少9,所以不发生变化。

【练习1】1.两个数相加，一个数减8,另一个数加8,和是否变化？2.两个数相加，一个数加3.另一个数也加3.和起什么变化？3.两个数相加，一个数减6,另一个数减2.和起什么变化？【例题2】两个数相加，如果一个加数增加10,要使和增加6,那么另一个加数应有什么变化？【思路】一个加数增加10,假如另一个加数不变，和就增加10。

现在要使和增加6,那么另一个加数应减少10 — 6=4。

【练习2】1.两个数相加，如果一个加数增加8,要使和增加15,另一个加数应有什么变化?2.两个数相加，如果一个加数增加8,要使和减少15,另一个加数应有什么变化?3.两个数相加，如果一个加数减少8,要使和减少8,另一个加数应有什么变化?【例题3】两数相减，如果被减数增加8,减数也增加8,差是否起变化？【思路】被减数增加8,假如减数不变，差就增加8；假如被减数不变，减数增加8, 差就减少8。

两个数的差先增加8,接着又减少8,所以不起什么变化。

【练习3】1.两数相减，被减数减少6,减数也减少6,差是否起变化？2.两数相减，被减数增加12.减数减少12.差起什么变化?3.两数相减，被减数减少10,减数增加10,差起什么变化?【例题4】两数相乘，如果一个因数扩大8倍，另一个因数缩小2倍，积将有什么变化？【思路】如果一个因数扩大8倍，另一个因数不变，积将扩大8倍；如果一个因数不变，另一个因数缩小2倍，积将缩小2倍。

积先扩大8倍又缩小2倍，因此，积扩大了 8 ・ 2=4 倍。

【练习4】1.两数相乘，如果一个因数缩小4倍，另一个因数扩大4倍，和是否起变化?2.两数相乘，如果一个因数扩大3倍，另一个因数缩小12倍，积将有什么变化?3.两数相乘，如果一个因数扩大3倍，另一个因数扩大6倍，积将有什么变化？【例题5】两数相除，如果被除数扩大4倍，除数缩小2倍，商将怎样变化？【思路】如果被除数扩大4倍，除数不变，商就扩大4倍；如果被除数不变，除数缩小2倍，商就扩大2倍。

人教版四年级数学上册方法技能分类评价4.积、商的变化规律及其应用一、认真审题，填一填。

(每小题4分，共20分)1.两个因数的积是120，其中一个因数乘4，如果另一个因数不变，这时积是( )，如果另一个因数乘2，积是( )。

2.两个数相乘，一个因数除以4，要使积不变，另一个因数应该( )。

3.两数相除，商是60，如果被除数除以2，除数乘2，商是( )；如果被除数除以2，除数除以2，商是( )。

4.两数相除，被除数乘8，要使商不变，除数应( )。

5.已知482÷6＝80……2，那么4820÷60＝( )……( )。

二、仔细推敲，选一选。

(每小题4分，共20分)1.480÷60和48÷6的商( )。

A.相等B.不相等C.无法确定2.两数相除，商是12，若被除数除以2，要使商不变，除数要( )。

A.除以2B.乘2C.不变3.一个除法算式，被除数不变，除数乘5，要使算式仍成立，商应( )。

A.除以5B.乘5C.无法判断4.A×B＝380，若A扩大到原来的10倍，则积是( )。

A.38B.3800C.380005.下列说法错误的是( )。

A. 被除数扩大到原来的10倍，除数扩大到原来的5倍，则商扩大到原来的2倍B. 两数相乘，一个因数扩大到原来的10倍，另一个因数扩大到原来的2倍，积扩大到原来的5倍C. 除法算式中，被除数除以4后，商是30，原来的商是120三、细心的你，算一算。

(共35分)1.计算出每组中第一题的结果，直接写出下面两题的结果。

(每小题1分，共9分)63÷9＝80÷5＝15×6＝630÷90＝240÷5＝15×12＝6300÷900＝480÷15＝45×12＝2.根据△÷□＝72，求出下列算式的结果。

(每空1分，共6分) (△×5)÷□＝( )△÷(□×6)＝( )(△×12)÷(□×12)＝( )(△÷72)÷(□÷72)＝( )(△×4)÷(□÷2)＝( )(△÷4)÷(□×2)＝( )3.根据规律做一做。

第10讲 变化规律（二）专题简析：积商的变化规律如下图所示（m ≠0）：例1:两数相乘，一个乘数扩大3倍，要使积扩大9倍，另一个乘数应该怎样变化？练习：1 、两数相乘，一个乘数缩小至原来的16，要使积扩大3倍，另一个乘数应该怎样变化？2、两数相乘，一个乘数扩大8倍，要使积缩小至原来的12，另一个乘数应该怎样变化？3、两数相乘，一个乘数缩小至原来的15，要使积缩小至原来的110，另一个乘数应该怎样变化？例2:两数相乘，积是96.如果一个乘数缩小至原来的14，另一个乘数扩大3倍，那么积是多少？练习：1、两数相乘，积是70.如果一个乘数扩大2倍，另一个乘数缩小至原来的15，那么积是多少？2、两数相乘，积是56.如果一个乘数缩小至原来的12，另一个乘数扩大3倍，那么积是多少？3、两数相乘，积是60.如果一个乘数扩大6倍，另一个乘数也扩大6倍，那么积是多少？例3:两数相除，如果被除数缩小至原来的13，除数扩大2倍，商将怎样变化？练习：1、两数相除，被除数扩大25倍，除数缩小至原来的115，商将怎样变化？2、 两数相除，被除数缩小至原来的15，除数缩小至原来的110倍，商将怎样变化？3、 两数相除，被除数扩大3倍，除数扩大15倍，商将怎样变化？例4:两数相除，被除数扩大30倍，要使商扩大60倍，除数应该怎样变化？练习：1、 两数相除，被除数缩小至原来的18，要使商扩大 2倍，除数应该怎样变化？2、两数相除，除数扩大9倍，要使商缩小至原来的13，被除数应该怎样变化？3、 两数相除，被除数缩小至原来的112，要使商缩小 至原来的12，除数应该怎样变化？例5:两数相除，商是4，余数是10.如果被除数和除数同时扩大50倍，商是多少？余数是多少？练习：1、两数相除，商是5，余数是15.如果被除数和除数同时扩大20倍，商是多少？余数是多少？2、两数相除，商是7，余数是3.如果被除数和除数同时扩大100倍，商是多少？余数是多少？3、两数相除，商是12，余数是120.如果被除数和除数同时缩小至原来的110，商是多少？余数是多少？课后练习1、两数相乘，一个因数扩大5倍，要使积缩小到原数的15，另一个因数应怎样变化？2、两数相乘，一个因数扩大到原数的12倍，要使积扩大到原数的3倍，另一个因数应怎样变化3、两数相乘，积是72，若一个因数缩小到原数的14，另一个因数缩小到原数的12，那么积是多少?4、两数相乗，积是150，若一个因数缩小到原数的110，另一个因数扩大到原数的6倍，那么积多少?5、两数相除，被除数打扩大到原数的3倍除数缩小到原数的14，商将怎样变化?6、两数相除，被除数着小到原数的120，除数缩小到原数的15，商会怎样变化?提优练习1、两数相除，被除数扩大15倍，要使商缩小到原数的13，除数应怎样变化?2、两数相除，除数缩小到原数的12，要使商缩小到原数的14，被除数应怎样变化?3、两数相除，被除数扩大5倍，要使商扩大10倍，除数应怎样变化?4、两数相除，商是24，余数是24。

2023-2024学年五年级数学上册典型例题系列之期中专项练习：积和商的规律（原卷版）1．两个因数的积是42.6，如果一个因数扩大到原来的100倍，另一个因数缩小到原来的110，那么积是( )。

2．5.21×1.87中，如果因数5.21扩大到原数的10倍，要使积不变，因数1.87应改为( )。

3．两个数相除的商是1.34，如果被除数扩大到原来的100倍，除数缩小到原来的1100，那么商是( )。

4．根据145×18＝2610在括号里填上适当的数。

14.5×( )＝2.61 ( )×0.18＝2.61 145×( )＝261( )×1.8＝26.1 1.45×( )＝2.61 ( )×18＝2.615．根据18×64＝1152，可知1.8×0.64＝( )，0.18×6.4＝( )。

6．已知9.18×a＝b，当a等于( )时，b＞9.18；当a等于( )时，b＜9.18；当a等于( )时，b＝9.18；当a等于( )，b＝0。

7．两个因数的积是17.8，若将其中一个因数扩大到原来的100倍，另一个因数缩小到原来的1100，则积为( )。

8．在（）中填上“＞”“＜”或“＝”。

4.92×0.01( )4.925.43×0.85( )5.436.18×1.01( )6.187.89×1.5( )78.9×0.159．两个因数相乘的积是47.5，如果一个因数扩大10倍，另一个因数不变，积就扩大( )倍，结果是( )。

10．3.7×a＝b，当a( )时，b小于3.7；当a( )时，b大于3.7。

11．两个因数相乘的积是27.5，如果一个因数扩大10倍，另一个因数扩大100倍，积就扩大（），结果是（）。

12．两个因数的积是12.05，其中一个因数不变，另一个因数缩小到它的1 100，积是( )。