积的变化规律与商的变化规律

四年级积商的变化规律5条一、积的变化规律。

1. 一个因数不变，另一个因数乘几，积也乘几。

- 例如：在算式3×5 = 15中，如果3不变，5变为5×2 = 10，那么积就变为3×10=30，15×2 = 30，积也乘了2。

- 在实际解决问题时，比如一个长方形的长不变，宽扩大到原来的3倍，根据长方形面积公式S =长×宽，面积也会扩大到原来的3倍。

2. 一个因数不变，另一个因数除以几（0除外），积也除以几。

- 例如：4×6 = 24，如果4不变，6变为6÷2 = 3，那么积就变为4×3 = 12，24÷2=12，积也除以了2。

- 假设每箱苹果的个数不变，箱数减少为原来的一半，那么苹果的总个数也会减少为原来的一半。

3. 两个因数同时乘一个数（0除外），积乘这个数的平方。

- 例如：2×3 = 6，如果2变为2×2 = 4，3变为3×2 = 6，那么新的积为4×6 = 24，而6×2^2=6×4 = 24。

- 在计算长方形面积时，如果长和宽都扩大到原来的2倍，那么面积就会扩大到原来的2×2 = 4倍。

4. 两个因数同时除以一个数（0除外），积除以这个数的平方。

- 例如：12×8 = 96，如果12变为12÷2 = 6，8变为8÷2 = 4，新的积为6×4 = 24，而96÷2^2 = 96÷4 = 24。

- 像把一个长方形的长和宽都缩小为原来的一半，面积就会缩小为原来的(1)/(4)。

二、商的变化规律。

1. 被除数不变，除数乘几（0除外），商就除以几。

- 例如：12÷3 = 4，如果被除数12不变，除数3变为3×2 = 6，那么商变为12÷6 = 2，4÷2 = 2，商除以了2。

积和商的“变与不变”规律㈠、积的变化规律：⑴、一个因数不变，另一个因数乘（或除以）几，积就相应的乘（或除以）几。

字母表示：若是a×b=c，则(a×3)×b=c×3举例：a×b=12若是(a×3)则积就是12×3=36.⑵、一个数乘一个比1大的数，积比原数大；⑶、一个数乘一个比1小的数，积比原数小。

㈡、积不变规律：一个因数乘（或除以）几，另一个因数相应的除以(或乘)几，积不变。

字母表示：若是a×b=c则（a×5）×（b÷5）=c㈢、商的变化规律：⑴被除数不变，除数乘几商就除以几，除数除以几商就乘几。

字母表示：若是a÷b=c，则a÷（b×3）=c÷3举例：a÷b=12若是(b×3)则商就是12÷3=4⑵除数不变，被除数乘商就相应的乘几，被除数除以几商就除以几。

字母表示：若是a÷b=c，则(a×3)÷b=c×3举例：a÷b=12若是(a×3)则商就是12×3=36.被除数大于除数，商就大于1；被除数小于除数，商就小于 1.一个数除以一个比1大的数，商比被除数要小；一个数除以一个比1小的数，商比被除数要大。

㈣、商不变规律：1被除数和除数同时乘或除以几，商不变。

其中专业理论知识内容包括：保安理论知识、消防业务知识、职业道德、法律知识、保安礼仪、救护知识。

作技术训练内容包括：岗位操作指引、勤务技术、消防技术、军事技术。

二．培训的及要求培训目的安全生产目标责任书为了进一步落实安全生产责任制，做到“责、权、利”相结合，依照我公司2015年度安全生产目标的内容，现与财务部签订以下安全生产目标：一、目标值：、全年人身死亡事故为零，重伤事故为零，小伤人数为零。

、现金安全保留，不发生盗窃事故。

积、商的变化规律+必考题积的变化规律有三条：1、一个因数不变，另一个因数扩大（或缩小）多少倍，积也扩大（或缩小）相同的倍数。

2、一个因数扩大（或缩小）多少倍，而另一个因数缩小（或扩大）相同的倍数，它们的积不变。

3、一个因数乘以（或除以）a，另一个因数乘以（或除以）b，积就乘以（或除以）ab的积。

商的变化规律有三条：1、被除数和除数同时扩大（或缩小）相同的倍数（0除外），商不变。

2、被除数不变，除数扩大多少倍，商反而缩小相同的倍数。

除数缩小多少倍，商反而扩大相同的倍数。

3、除数不变，被除数扩大多少倍，商扩大相同的倍数。

被除数缩小多少倍，商缩小相同的倍数。

必考题：1、三位数除以两位数的算式口73÷58，如果商是两位数，那么口里最小填（6），如果商是一位数，口里可以有（5）种不同的填法。

2、一辆汽车8小时行驶了500千米，照这样计算，这辆汽车40小时能行驶（2500）千米。

积、商的变化规律+必考题3、一个除法算式的被除数和除数都乘3后，商是36，那么原来的商是（36）4、两个数的商是6，如果被除数不变，除数除以6，那么商应是（36）。

5、两个数的积是40，如果一个因数扩大10倍，另一个因数扩大5倍，那么积应该是（2000）。

6、根据32×16=512，直接写出下面各式的积。

320×160=（51200 ）320×1600=（512000）32×160=（5120）1600×160=（256000）16×8=（128）0.32×16=（ 5.12）7、根据5376÷56=96，直接写出下面各式的商。

537600÷56=（9600）5376÷112=（48 ）2688÷28=（96）268800÷56=（4800）5376÷14=（38）5376÷5600=（0.96 ）积、商的变化规律+必考题8、判断对错。

积和商的“变与不变”规律㈠、积的变化规律：⑴、一个因数不变,另一个因数乘（或除以)几，积就相应的乘（或除以）几。

字母表示:如果a×b＝c ,则(a×3)×b=c×3举例:ａ×b＝1２如果(a×3)则积就是12×3=3６.⑵、一个数乘一个比1大的数,积比原数大；⑶、一个数乘一个比1小的数,积比原数小。

㈡、积不变规律：一个因数乘（或除以)几，另一个因数相应的除以（或乘)几,积不变。

字母表示:如果a×b=c 则（a×5）×(ｂ÷５）=c㈢、商的变化规律：⑴被除数不变,除数乘或除以几，商就相应的除以或乘几。

字母表示:如果a÷ｂ＝ｃ,则ａ÷（ｂ×３)=c÷3举例:a÷ｂ=1２如果(ｂ×３)则商就是1２÷３=4⑵除数不变，被除数乘或除以几，商就相应的乘或除以几。

字母表示：如果a÷ｂ=c ,则(a×3）÷b=c×3举例：a÷b＝12 如果(a×3)则商就是１2×3=3６.被除数大于除数,商就大于1;被除数小于除数，商就小于1．一个数除以一个比１大的数，商比被除数要小;一个数除以一个比１小的数，商比被除数要大。

㈣、商不变规律：被除数和除数同时乘或除以几，商不变。

[问题一]两数相乘,如果一个因数乘３,另一个因数除以12，积将有什么变化？想:如果一个因数扩大３倍,另一个因数不变,积将扩大3倍；如果一个因数不变，另一个因数缩小12倍，积将缩小12倍。

积扩大3倍又缩小１2倍，因此，积缩小了12÷3=４倍。

解：12÷3=4答:积缩小了４倍。

[试一试]１、两数相乘,如果一个因数缩小5倍，另一个因数扩大5倍,积是否起变化?２、两数相乘，积是36，如果一个因数扩大２倍,另一个因数缩小3倍，那么积是多少？３、两数相乘,积是72如果一个因数扩大４倍，另一个因数缩小3倍，那么积是多少?[问题二]两个数相除,被除数扩大30倍，除数缩小6倍，商将怎样变化?想：如果被除数扩大30倍，除数不变，商将扩大30倍;如果被除数不变,除数缩小6倍，商将扩大6倍;商先扩大30倍,又扩大6倍，商将扩大3０×6=１8０倍。

和、差、积、商的变化规律1、和的变化规律（1）如果一个加数增加（或减少）一个数，另一加数不变，那么它们的和也增加（或减少）同一个数。

用字母表示：a+b= c→(a+m)+b=c+m或(a-m)+b=c-m(2)如果一个加数增加一个数，另一个加数减少同一个数，那么它们的和不变。

用字母表示：a+b=c→(a+m)+(b-m)=c2、差的变化规律（1）如果被减数增加（或减少）一个数，减数不变，那么它们的差也增加（或减少）一个数。

用字母表示：a-b= c→（a+ m）- b= c+ m或a- b= c→（a- m）- b = c- m（2）如果被减数不变，减数增加（或减少）一个数，那么它们差反而减少（或增加）同一个数。

用字母表示：a- b= c→a-（b+ m）= c- m或a-（b- m）= c+ m（3）如果被减数和减数都增加（或减少）同一个数，那么它们的差不变。

用字母表示：a- b= c→（a+ m）-（b+ m）= c或（a- m）-（b- m）= c3、积的变化规律（1）一个因数扩大（或缩小）若干倍，另一个因数缩小（或扩大）相同的倍数，积不变。

用字母表示：a×b=c→（a×m）×（b÷m）=c或（a÷m）×（b×m）=c（2）一个因数扩大（或缩小）若干倍，另一个因数不变，积也扩大（或缩小）相同的倍数。

用字母表示：a×b=c→（a×m）×b=c×m或（a÷m）×b=c÷m4、商的变化规律（1）商不变的性质：在除法里，被除数和除数同时乘或除以相同的数（0除外），商不变。

用字母表示：a÷b=c→（a×m）÷（b×m）=c或（a÷m）÷（b÷m）=c（2）除数不变，被除数扩大（或缩小）若干倍，商也扩大（或缩小）相同的倍数。

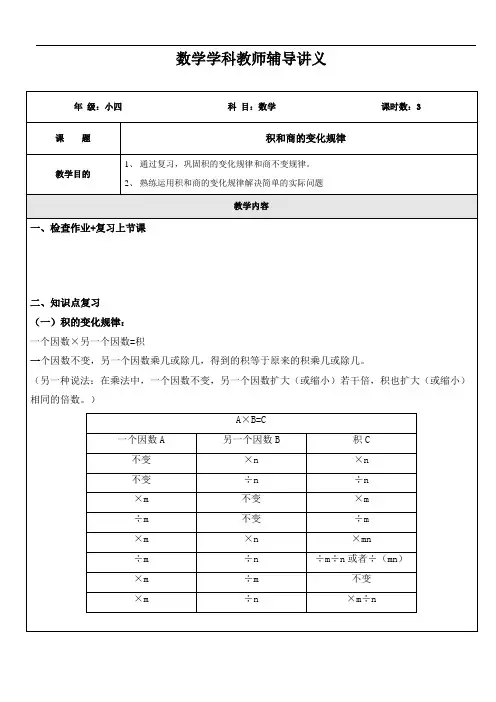
积和商“变与不变”规律及练习积和商的“变与不变”规律积的变化规律：1.一个因数不变，另一个因数乘（或除以）几，积就相应的乘（或除以）几。

例如：如果a×b=c，则(a×3)×b=c×3，举例：a×b=12，如果(a×3)，则积就是12×3=36.2.一个数乘一个比1大的数，积比原数大；一个数乘一个比1小的数，积比原数小。

积不变规律：1.一个因数乘（或除以）几，另一个因数相应的除以(或乘)几，积不变。

例如：如果a×b=c，则（a×5）×（b÷5）=c。

商的变化规律：1.被除数不变，除数乘或除以几，商就相应的除以或乘几。

例如：如果a÷b=c，则a÷（b×3）=c÷3，举例：a÷b=12，如果(b×3)，则商就是12÷3=4.2.除数不变，被除数乘或除以几，商就相应的乘或除以几。

例如：如果a÷b=c，则(a×3)÷b=c×3，举例：a÷b=12，如果(a×3)，则商就是12×3=36.被除数大于除数，商就大于1；被除数小于除数，商就小于1.一个数除以一个比1大的数，商比被除数要小；一个数除以一个比1小的数，商比被除数要大。

商不变规律：被除数和除数同时乘或除以几，商不变。

练题：1.根据78×12＝936，填写下面各题的结果。

7.8×12＝(93.6)，0.78×12＝(9.36)，7.8×(93.6)＝(734.88)2.根据414÷18＝23，填写下面各题的结果。

4.14÷1.8＝(2.3)，4140÷1.8＝(2300)，0.414÷0.18＝(2.3)，41.4÷18＝(2.3)3.根据45×63＝2835，填写下面各题的结果。

《积和商的变化规律》必考考点积的变化规律有三条：1、一个因数不变，另一个因数扩大（或缩小）多少倍，积也扩大（或缩小）相同的倍数。

2、一个因数扩大（或缩小）多少倍，而另一个因数缩小（或扩大）相同的倍数，它们的积不变。

3、一个因数乘以（或除以）a，另一个因数乘以(或除以）b，积就乘以（或除以）ab的积。

商的变化规律有三条：1、被除数和除数同时扩大（或缩小）相同的倍数（0除外），商不变。

2、被除数不变，除数扩大多少倍，商反而缩小相同的倍数。

除数缩小多少倍，商反而扩大相同的倍数。

3、除数不变，被除数扩大多少倍，商扩大相同的倍数。

被除数缩小多少倍，商缩小相同的倍数。

必考题：1、三位数除以两位数的算式口73÷58，如果商是两位数，那么口里最小填(6），如果商是一位数，口里可以有(5)种不同的填法。

2、一辆汽车8小时行驶了500千米，照这样计算，这辆汽车40小时能行驶（2500）千米。

《积和商的变化规律》必考考点3、一个除法算式的被除数和除数都乘3后，商是36，那么原来的商是（36）4、两个数的商是6，如果被除数不变，除数除以6，那么商应是（36）。

5、两个数的积是40，如果一个因数扩大10倍，另一个因数扩大5倍，那么积应该是（2000）。

6、根据32×16=512，直接写出下面各式的积。

320×160=( 51200 )320×1600=( 512000 )32×160=(5120 )1600×160=(256000 )16×8=(128 )0.32×16=(5.12 )7、根据5376÷56=96，直接写出下面各式的商。

537600÷56=( 9600 )5376÷112=( 48 )2688÷28=( 96 )268800÷56=( 4800 )5376÷14=( 38 )5376÷5600=( 0.96 )。