下载文档原格式
一、微分元素法)( 或称为积分元素法法数学建模中的微分元素 ,当把非均匀变化的问题实际中在物理、几何以及工程 , ,则通积达形式能表示为某两个量的乘看作是均匀变化时. 分问题来处理常可将问题归结为定积 . 具有对区间的可加性要求量运用定积分处理问题时A取极限”—求和—近似“分划—,局利用整体上变化的量在局部问题的步骤将整体问题化成 , ,替“变”在局部上以“不变”代关系部上近似于不变的辩证,采用按照定积分的概念]. ,[ )( 111i i i ni i i ni i x x x f A A −==∈∆≈∆=∑∑ξξ便有关系式, ,个将具有代表性的第略去下标为简便和醒目起见i i, , ]d ,[ ] ,[ 1且取称之为典型小区间表示为小区间x x x x x i i +−, 则有为区间的左端点x i ξ. d )(x x f A ≈∆, )( d )( 记为或积分元素的微分元素为量通常称A x x f. d )(d x x f A =( 0d , 相当于取极限过程对区间的可加性由量→x A ] ,[ d , 0)||||上“无限累加”起来在区间将微分元素b a A x →∆] ,[ )(上的值：在区间就得到量即作定积分b a A. d )(d ∫∫==babax x f A A. ,加解为微分元素的无限累我们在这里将定积分理简言之一、平面图形的面积1解解解解y2解3解二、旋转体的体积一轴旋转一周所生成的将平面图形绕平面上某 . ,该轴称为旋转轴几何体称为旋转体 . , 间的可加性旋转体的体积具有对区上在区间I:旋转体的特点 ,截旋转体所得的的平面任何一个垂直于旋转轴. 图形均为圆截口1 y1 y2解Oaa b解解2πy三、平行截面面积为已知的几何体的体积解解。
定积分的几何应用定积分是微积分中的重要概念，它有着广泛的应用。
其中之一就是在几何学中的应用。
本文将探讨定积分在几何学中的具体应用，并解释其背后的原理和意义。
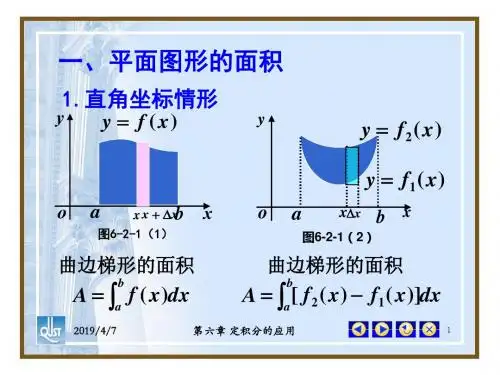
一、平面图形的面积通过定积分，我们可以计算出复杂平面图形的面积。
假设有一个曲线方程y=f(x)，该曲线与x轴所围成的图形为A。
我们可以将A分解成无限个极小的矩形条，然后通过求和的方式来逼近A的面积。
具体而言，我们可以将横轴x划分为n个小区间，每个小区间的宽度为Δx。
然后，在每个小区间中，选择一个x值作为代表点，记作xi。
根据代表点xi和函数f(x)的值，我们可以计算出相应小矩形的高度为f(xi)。
由于每个小矩形的宽度Δx非常小，因此在计算总面积时，可以通过求和的方式逼近。
即可以得到如下的定积分表达式：A = ∫[a,b] f(x) dx其中[a,b]表示x的取值范围。
通过对上述定积分进行求解，即可得到图形A的面积。
二、曲线的弧长除了计算平面图形的面积外，定积分还可以用来计算曲线的弧长。
假设有一个曲线L，其方程为y=f(x)。
我们希望计算出曲线L的弧长。
与计算面积类似，我们同样可以将曲线L分解为无限个极小的线段，然后通过求和的方式来逼近曲线L的弧长。
具体而言，我们可以将横轴x划分为n个小区间，每个小区间的宽度为Δx。
然后，在每个小区间中，选择一个x值作为代表点，记作xi。
根据代表点xi和函数f(x)的值，我们可以计算出相应线段的长度为Δs。
同样地，由于每个小线段的长度Δs非常小，因此在计算总弧长时，可以通过求和的方式逼近。
即可以得到如下的定积分表达式：L = ∫[a,b] √(1 + [f'(x)]^2) dx其中[a,b]表示x的取值范围，f'(x)表示函数f(x)的导数。
通过对上述定积分进行求解，即可得到曲线L的弧长。
三、体积与质量除了平面图形的面积和曲线的弧长外，定积分还可以用来计算体积和质量。
当我们需要计算一个曲线绕某个轴旋转一周所形成的立体的体积时，定积分就派上用场了。
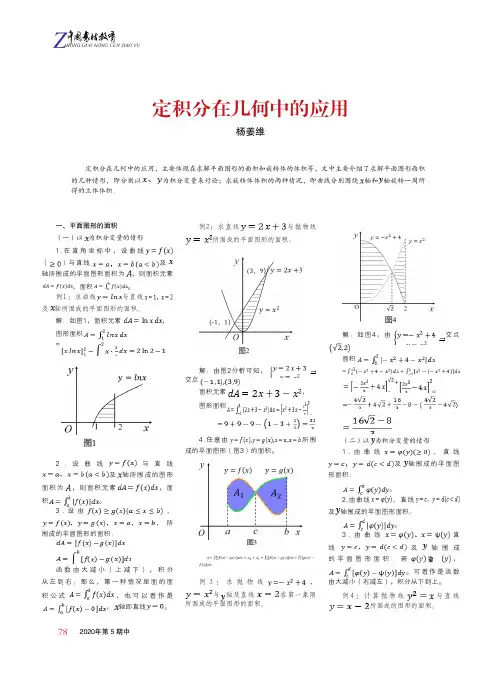
782020年第 5 期中定积分在几何中的应用杨姜维一、平面图形的面积（一）以为积分变量的情形1.在直角坐标中，设曲线（）与直线及轴所围成的平面图形面积为，则面积元素，面积。
例1：求曲线与直线及轴所围成的平面图形的面积。
解：如图1，面积元素，图形面积=2.设曲线与直线及轴所围成的图形面积为，则面积元素，面积。
3.设由，所围成的平面图形的面积：函数由大减小（上减下），积分从左到右；那么，第一种情况里面的面积公式，也可以看作是，轴即直线。
例2：求直线与抛物线所围成的平面图形的面积。
解：由图2分析可知，交点面积元素，图形面积4.任意由所围成的平面图形（图3）的面积。
例3：求抛物线，与轴及直线在第一象限所围成的平面图形的面积。
解：如图4，由交点面积+（二）以为积分变量的情形1.由曲线、直线及轴围成的平面图形面积：。
2.由曲线、直线及轴围成的平面图形面积：。
3.由曲线直线及轴围成的平面图形面积：若，。
可看作是函数由大减小（右减左），积分从下到上。
例4：计算抛物线与直线所围成的图形的面积。
定积分在几何中的应用，主要体现在求解平面图形的面积和旋转体的体积等，文中主要介绍了求解平面图形面积的几种情形，即分别以为积分变量来讨论；求旋转体体积的两种情况，即曲线分别围绕轴和轴旋转一周所得的立体体积。
JIAO HAI TAN HANG／教海探航解：如图5，由交点为方便计算，选取为积分变量，则有4.任意由曲线直线及轴围成的平面图形面积：。
二、旋转体的体积一个平面图形围绕其所在平面上的一条直线旋转一周而成的立体即为旋转体，常见的旋转体有圆柱体、圆锥、圆台、球体等,这些都有对应的体积公式，面对日常生活中所用到的水杯、花瓶等立体物件，求解体积时可考虑以下情况：（一）曲线绕轴旋转的情形由连续曲线与直线及轴所围成的曲边梯形绕轴旋转一周而成的立体，选为积分变量，该旋转体的体积元素，体积为。
（二）曲线绕轴旋转的情形由曲线、直线及轴围成的平面图形绕轴旋转一周所得的立体，选为积分变量，该旋转体的体积元素，体积为。
定积分在几何,物理学中的简单应用
定积分是一种常见的数学工具，用来解决许多几何和物理问题。
它可以在几何学、物理学中解决积分、面积和容积计算题中应用。
首先，定积分在几何学中的简单应用。
比如，如果我们要计算一个几何图形的面积，则可以通过定积分来计算。
它可以计算任意形状的几何图形的面积，比如三角形、椭圆、圆形等。
它的应用范围非常广泛，比如可以用它来计算面积、周长、体积等。
其次，定积分也可以用在物理学中。
比如，如果我们要计算一个物体在多次不同力作用之下移动的路程，可以用定积分来计算。
它可以帮助我们精确地计算物体受力作用前后的距离，也可以帮助我们精确计算弹性作用力等。
最后，定积分也可以应用于物理学的温度问题中。
比如，我们可以通过定积分求出一个物体在单位温差下的热量传递，也可以求出一个物体的总热量。
还可以用它求解温度场、热传导率、热导率等问题。
以上是定积分在几何、物理学中的简单应用。
定积分是一种通用而有效的数学工具，在几何、物理学中都有着广泛的应用，不仅可以用来解决相关的面积、容积计算题，而且还可以用来解决物理热力学、温度等问题。
只要我们掌握它的基本使用方法以及它的一些特性和用途，就可以在几何、物理学中更好地应用它来解决其它问题。
- 1 -。
定积分的基本性质及应用定积分是微积分的重要概念之一，它在数学和各个学科中都有广泛的应用。
本文将重点介绍定积分的基本性质和在实际问题中的应用，并且通过具体的例子来加深理解。
定义：定积分是对一个函数在闭区间上的加权平均值进行求和的过程。
在数学中，一个函数f(x)在[a, b]上的定积分表示为：∫(a to b) f(x) dx其中，∫代表求和的过程，a和b是积分的上下限，f(x)是被积函数。
基本性质：1. 线性性质：定积分具有线性性质，即对于任意两个函数f(x)和g(x)，以及任意的实数k，有以下等式成立：∫(a to b) (f(x) + g(x)) dx = ∫(a to b) f(x) dx + ∫(a to b) g(x) dx∫(a to b) k*f(x) dx = k * ∫(a to b) f(x) dx2. 区间可加性：如果一个函数在闭区间[a, b]上有定义，且在其中一个点c上可导，则该函数在[a, b]上的定积分等于该函数在子区间[a, c]和[c, b]上的定积分之和：∫(a to b) f(x) dx = ∫(a to c) f(x) dx + ∫(c to b) f(x) dx3. 积分中值定理：如果一个函数f(x)在闭区间[a, b]上连续，且在该区间内不恒为0，那么至少存在一个点c，使得：∫(a to b) f(x) dx = f(c) * (b - a)4. 边界性质：对于定积分∫(a to b) f(x) dx，当a等于b时，定积分的值为0。
若a小于b，则定积分的值为正数或负数，具体取决于函数f(x)在[a, b]上的正负性。
5. 非负性质：如果一个函数f(x)在闭区间[a, b]上连续且非负，那么定积分的值也是非负的。
应用：定积分在实际问题中有着广泛的应用，下面将介绍两个具体的应用。
1. 几何应用：定积分可以用于计算曲线与坐标轴之间的面积。
如果一个函数在闭区间[a, b]上非负，那么该函数与x轴围成的曲边梯形的面积可以通过定积分来计算：面积= ∫(a to b) f(x) dx同样的，若函数f(x)在闭区间[a, b]上非正，那么面积可以表示为定积分的绝对值。
定积分的几何应用教学内容与曲边形的面积、变速直线运动的路程一样，自然科学、社会科学和生产实践中出的一大类量都是累积效应的结果，它们可以用Riemann 和式的极限来刻画，即用定积分来度量。
本节讲解定积分的几何应用，主要是以下几方面的内容：（1） 微元法；（2） 平面图形的面积；（3） 已知平行截面面积的立体体积和旋转体的体积； （4） 曲线的弧长及其曲率； （5） 旋转曲面的面积。
教学思路和要求（1）微元法是由局部性态的讨论最后合成整体的累积效应、即定积分的方法，要详细讲透其思想，使学生在今后能够举一反三地使用；（2）在用推导公式时，注意说明选取微元的着眼点与理由，并注意说明整体微元如何导出，使学生学会灵活运用微元法；（3）注意几何背景的说明，并结合实际例子说明一些图形的特点与画法，以及积分区间的选取；（4）注意指出对于复杂的几何图形，在计算时要具体问题具体分析，可能要分几部分来讨论，不能直接套用公式。
最好举例说明处理方法。
教学安排一．微元法为说明具有哪些特征的量有望用定积分刻画，我们再度分析一下⎰=ba dtt f I )(的概念。
首先，对固定的函数f ，I 取决于积分区间。
定积分具有一个十分重要的性质：可加性，即],[b a 被分为许多部分小区间，则I 被相应地分成许多部分量i I ∆，总量I 等于诸部分量之和，即∑∆=i I I 。
凡能用定积分描述的量都应具有这种可加性的特征。
其次，由于可加性，问题便化为部分量I ∆的计算。
对连续函数f ，记⎰=xadt t f x I )()(，则有)()(x f x I ='，所以)()()()(dx o dx x f x I x x I I +=-∆+=∆。
由此可见，对于能用定积分刻画的量，其在区间微元],[dx x x +上的部分量应能近似地表现为dx 的线性函数，即dx x f I )(≈∆，而且其误差应是比dx 高阶的无穷小。
上面的dx 是自变量的微分，在应用中常被称作x 的微元。
它是一个变量。
一方面，在变化过程的每一时刻，即相对静止时，它是一个有限量；另一方面，其变化趋势则以0为极限，即是一个无穷小量。
记微分形式dx x f )(为dI ，在应用中常被称作量)(x I 的微元。
总量I 即是微元dx x f dI )(=的积分。
我们宁愿把dx x f )(称作微元，而不直接称为I 的微分，原因在于实际应用时，往往和上述由积分I 导出微元dI 的过程相反，微元法是由微元dx x f )(出发导出积分，即由局部性态的讨论最后合成整体的累积效应。
如果我们要处理某个量I ，它与变量x 的变化区间],[b a 有关，而且 （1） 满足关于区间的可加性，即整体等于局部之和；（2）它在],[dx x x +上的部分量I ∆近似于dx 的一个线性函数，即)(dx o dI I =-∆，其中dx x f dI )(=称之为量I 的微元。
那么，以微元dx x f dI )(=为被积表达式，作积分即得⎰=badx x f I )(。
诸如弧长、面积、体积、引力、压力、功等几何量和物理量都具有某种可加性，且其小增量均可用微元近似表示，从而它们都可用定积分计算。
在应用问题中往往略去关于)(dx o dI I =-∆的验证。
二．面积问题（直角坐标下的区域）考察由曲线)(x f y =，)(x g y =和直线a x =，b x =（b a <）所围平面图形的面积。
先设g f ≥，变量x 的变化区间为],[b a 。
显然，面积具有关于区间的可加性。
在区间微元],[dx x x +上，相应的小曲边形（图3.4.1中阴影部分）面积A ∆近似等于高为)()(x g x f -，宽为dx 的矩形面积，即 dx x g x f A )]()([-≈∆， 所以，面积微元为dx x g x f dA )]()([-=。
于是，所求的面积⎰-=badx x g x f A )]()([。
如果删去条件g f ≥，同样可得 dx x g x f dA |)()(|-=， 从而⎰-=badx x g x f A |)()(|。
例3.4.1 求由抛物线2x y =及直线x y 3=所围图形的面积（图3.4.2）。
解 先求出两曲线交点为)0,0(和)9,3(。
如果以x 为积分变量，取积分区间为]3,0[，有=-=⎰302)3(dx x x A 2931233032=⎪⎭⎫ ⎝⎛-x x 。
如果以y 为积分变量，则应取积分区间为]9,0[，此时⎰⎪⎭⎫ ⎝⎛-=903dy y y A xy 图3.4.229233290223=⎪⎪⎭⎫ ⎝⎛⋅-=y y 。
三．面积问题（极坐标下的区域）考察介于曲线)(θr r =与射线αθ=和βθ=（πβα20≤<≤）间的曲边扇形的面积，其中)(θr 是连续函数（图3.4.3）。
以θ为积分变量，在区间微元],[θθθd +上对应的小曲边扇形的面积近似于圆扇形的面积，即θθd r A 2)]([21≈∆，所以面积微元θθd r dA 2)]([21=，于是⎰=βαθθd r A 2)]([21。
例 3.4.2 计算心脏线)cos 1(θ+=a r （πθπ≤≤-）所围区域的面积（图3.4.4）。
解 由图形的对称性，只要计算该图形的上半部分的面积，其两倍便是所求图形的面积。
由面积计算公式得⎰+⋅=πθθ022)cos 1(212d a A⎰=πθθ0422cos 4d a⎰=2042c o s 8πθθd a2223224138a a ππ=⋅⋅⋅⋅=。
四．已知平行截面面积求体积设空间立体Ω介于过a x =和b x =点且垂直于x 轴的两平面之间，已知它被过x 点且垂直于x 轴的平面所截出的图形的面积为)(x A （图3.4.5）。
显然，在区间微元],[dx x x +上，Ω的体积微元为一母线与x 轴平行、高为dx ，底面积为)(x A 的柱体体积，即dx x A dV )(=， 所以⎰=badx x A V )(。
例3.4.3 已知一直圆柱体的底面半径为R ，一斜面1π过其底面圆周上一点，且与底面2π成夹角θ，求圆柱被1π，2π所截得部分的体积。
解 取圆柱底面圆周中心为原点，底面2π为xy 平面，1π与圆周交点在y 轴上（图3.4.6）。
这样，对x图3.4.5],[R R y -∈，过)0,,0(y 且与y 轴重直的平面与圆柱被截部分的截面是一个矩形，它的底为222y R -，高为θtan )(R y +。
因此θt a n)(2)(22R y y R y A +-= 所求体积为⎪⎭⎫ ⎝⎛-+-=⎰⎰--RR R R dy y R R dy y R y V 2222tan 2θ。
括号中第一项是一个奇函数在对称区间上的积分，其值为0；第二项的积分恰为半径为R 的上半个圆的面积，因此θπtan 3R V =。
读者不难发现，如用与x 轴垂直的平面与之相截,截面是直角梯形，用与z 轴垂直的平面与之相截，截面则是弓形，处理都会繁复一些。
因而应对不同问题作具体分析，寻求事半功倍的最佳方案。
五．旋转体的体积由已知平行截面面积计算体积的公式有一个直接的推论，这就是求旋转体体积的公式。
设空间立体Ω为由平面图形}),(0|),{(b x a x f y y x ≤≤≤≤绕x 轴旋转一周而成的旋转体（图3.4.7）。
如用在点)0,(x 处与x 轴垂直的平面截此立体，所得截面显然是一个半径为)(x f 的圆，即截面积为2)]([)(x f x A π=。
因此⎰=badx x f V 2)]([π。
例3.4.4 求椭圆12222=+b y a x 所围图形绕x 轴旋转一周所得椭球的体积。
解 由于22x a aby -=，利用对称性可得⎰⎰-==a adx x a ab dx y V 0222202)(22ππ2032223432ab x x a ab aππ=⎪⎪⎭⎫ ⎝⎛-=。
当b a =时，就得到以a 为半径的球体积为334a π。
六．曲线的弧长设有曲线L 的方程为)(x f y =（b x a ≤≤），其中f 具有连续导数。
今欲求其弧长s （图3.4.8）。
用微元法。
设区间微元],[dx x x +对应于小弧段PQ ，该弧段之长s ∆可用它在P 处切线段PT 的长度来近似，即22)()(dy dx ds s +=≈∆dx x f 2)]([1'+=。
于是曲线L 的弧长为dx x f s b a⎰'+=2)]([1。
当弧L 用参数方程⎩⎨⎧==),(),(t y y t x x βα≤≤t 表示时，dt t x dx )('=，dt t y dy )('=。
从而()dt t y t x dy dx ds 2222)]([)]([)('+'=+=，进而dt t y t x s a⎰'+'=β22)]([)]([。
当曲线L 用极坐标方程)(θr r =， βθα≤≤表示时，由于⎩⎨⎧==,sin )(,cos )(θθθθr y r x 便得θθθd r r dx )sin cos (-'=，θθθd r r dy )cos sin (+'=，从而θd r r dy dx ds 2222)()('+=+=，进而⎰'+=βαθd r r s 22。
例3.4.5 求曲线段2332x y =（31≤≤x ）的弧长。
解 由dx x dx y ds +='+=1)(12得图3.4.8312331)1(321x dx x s +=+=⎰)228(32-=。
例3.4.6 求心脏线)cos 1(θ+=a r 的周长，其中0>a 。
解 由对称性 ='+=⎰πθ022)(2d r r s ⎰+πθθ0cos 222d a==⎰πθθ02cos 4d a a a 82sin80=πθ。
例3.4.7 求椭圆12222=+by a x （0>>b a ）的周长。
解 椭圆的参数方程为⎩⎨⎧==,sin ,cos θθb y a x πθ20≤≤。
由对称性，其周长等于它落在第一象限部分的4倍，故⎰+=202222cos sin 4πθθθd b a s ⎰-=2022cos 14πθθεd a ，其中ab a 22-=ε为椭圆的离心率。
椭圆周长表达式中出现的积分⎰-2022cos 1πθθεd （10<<ε）称为第二类椭圆积分。
由于被积函数θε22cos 1-的原函数不能用初等函数来表示，因而椭圆周长必须用数值积分的方法计算。
七．旋转曲面的面积 设曲线L 的方程为)(x f y =， b x a ≤≤。
