当前位置：文档之家 › 定积分在几何中的应用 课件

定积分在几何中的应用 课件

  • 格式：ppt
  • 大小：1.58 MB
  • 文档页数：26

下载文档原格式

  / 26

合集下载

【全程复习方略】2014-2015学年高中数学 1.7.1 定积分在几何中的应用课件 新人教A版选修2-2

【全程复习方略】2014-2015学年高中数学 1.7.1 定积分在几何中的应用课件 新人教A版选修2-2

排除A；当阴影有在x轴上方也有在x轴下方时，a f(x)dx是两
面积之差，排除B；无论什么情况C都对，故应选C.
b
【误区警示】曲线f(x)与直线x=a，x=b，y=0围成图形的面积 不能均用 f(x)dx表示，要根据图形位置分不同情况选用适当
a b
的积分值表示.
【补偿训练】过原点的直线l与抛物线y=x2-2ax(a>0)所围成的 图形面积为 9 a3，则直线l的方程为(
【方法技巧】求函数图象围成平面图形面积的方法 (1)画出两个函数的图象，先将两个函数方程联立方程组求解， 得到函数图象的交点的横坐标a，b(a<b)，确定积分区间[a， b]. (2)在公共的积分区间上，由上界函数减去下界函数作为被积
函数，定积分的值就等于两个函数图象围成平面图形的面积，
即S= [f1(x)-f2(x)]dx(其中f1(x)>f2(x)).
(2-x)dx.
1 2
2
(3)正确，曲线y=3-x2与直线y=-1的交点为(-2，-1)，
(2，-1)，所以围成的图形面积为 2［(3-x2)-(-1)］dx=

2
2
(4-x2)dx. (2)√ (3)√
答案：(1)×
2.做一做(请把正确的答案写在横线上)
(1)如图中阴影部分的面积是____________.
b
1.判一判 (正确的打“√”，错误的打“×”) (1)曲线y=sin x，x∈[ ， ]，与x轴围成的图形的面积为
3 2 2

3 2 2
sin xdx.(
)
1 0
(2)曲线y=x3与直线x+y=2，y=0围成的图形面积为 x3dx+

定积分的应用平面曲线弧长课件

定积分的应用平面曲线弧长课件
参数方程中的x(t)和y(t)表示曲线上某一点在x和y方向上的坐标，t表示该点在曲 线上的位置。
参数方程的转换
参数方程转换为普通方程
将参数方程中的参数t消除，将参数方程转换为普通方程。
参数方程的微分形式
将参数方程转换为微分形式，以便于计算曲线的切线斜率和 弧长。
03 定积分在平面曲线弧长中 的应用
理论完善
随着定积分在平面曲线弧长中的应用越来越广泛，其理论体系也可能会得到进一步完善。例如，可能会发现新的定理 和公式，以更好地描述和解决定积分问题。
应用领域的拓展
随着科技的不断发展，定积分的应用领域也可能会进一步拓展。例如，在人工智能、机器学习等领域中， 定积分可能会被用来解决一些新的问题。
定积分在平面曲线弧长中的实际价值
弧长公式的应用
计算特定曲线的弧长
利用弧长公式，可以计算出给定参数 方程的曲线上任意一段弧的长度。这 迹的长度 等。
比较不同曲线的长度
通过比较不同曲线的弧长，可以得出 它们之间的形状差异。例如，可以利 用弧长公式比较不同函数的图像长度。
弧长公式的拓展
弧长公式的推导
弧长公式的基本概念
弧长公式是定积分的一个重要应用，它用于计算平面曲线上某段弧的长度。在推 导弧长公式之前，需要了解曲线的基本参数方程和弧长的定义。
弧长公式的推导过程
通过将曲线分割成许多小段，并利用定积分计算每小段线段的长度，然后将这些 长度相加，最终得到整个弧的长度。这个过程涉及到极限和定积分的概念。
建立方程
首先需要确定曲线的起点和终点，以 及曲线在起点和终点处的切线方向。
根据起点、终点和参数，建立曲线的 参数方程。
选择参数
选择一个合适的参数，例如时间或角 度，来表示曲线上每一点的位置。

高中数学-定积分在几何中的应用-课件

高中数学-定积分在几何中的应用-课件

求由一条曲线 y＝f(x)和直线 x＝a，x＝b(a<b)及 y＝0 所围成平面图形的面积 S.
①如图 1 所示，f(x)>0， bf(x)dx>0. a
∴S＝ bf(x)dx. a
②如图 2 所示，f(x)<0， bf(x)dx<0， a
∴S＝| bf(x)dx|＝－ bf(x)dx.
a
a
2×23x32
|
2 0
＝136，
8
S2＝2 [4－x－(－ 2x)]dx
＝4x－12x2＋2
3
2x32|
8 2
＝338，
于是 S＝136＋338＝18.
方法二：选y作为积分变量，
将曲线方程写为x＝y22及x＝4－y.
则S＝2－44－y－y22dy
＝4y－y22－y63|
2 －4
＝18.
变式训练 1：由曲线 y＝ x，直线 y＝x－2 及 y 轴所围成
解．
由方程组
y2＝2x y＝4－x
解出抛物线和直线的交
点为(2,2)及(8，－4)．
方法一：选 x 作为积分变量，由图可看出 S＝S1＋S2，
由于抛物线在 x 轴上方的方程为 y＝ 2x，
在 x 轴下方的方程为 y＝－ 2x，
2
所以 S1＝0 [ 2x－(－ 2x)]dx
＝2
2 1
20x2 dx＝2
❖1．7 定积分的简单应用
❖1.7.1 定积分在几何中的应用
自主学习 新知突破
❖ 1．理解定积分的几何意义．
❖ 2．会通过定积分求由两条或多条曲线 围成的平面图形的面积．
复习回顾
[问题 1]定积分的几何意义．
由三条直线 x＝a，x＝b(a<b)，x 轴及 一条曲线 y＝f(x)(f(x)≥0)围成的曲边 梯形的面积 S＝________.

高数课件第六章定积分的应用：第二节定积分的几何应用

高数课件第六章定积分的应用：第二节定积分的几何应用

y
c
b O
x
bx
x
x x 1 sh dx ch dx c c b x xb s 2 ch dx 2c sh 0 c c 0 x b 1 x 2c sh ( c ch ) c sh c c c c
2
e e ch x 2 x x e e sh x 2 (ch x) sh x
Hale Waihona Puke 2 (t ) 2 (t ) d t
因此所求弧长
s


2 (t ) 2 (t ) d t
(3) 曲线弧由极坐标方程给出:
令 x r ( ) cos , y r ( ) sin , 则得
dx [r ( ) cos r ( ) sin ]d dy [r ( ) sin r ( ) cos ]d
2
选 x 为积分变量 (1) x [2, 0], dA1 ( x 3 6 x x 2 )dx 于是所求面积 A A1 A2
特别注意:
各积分区间 A ( x 3 6 x x 2 )dx 0 (x x 6 x)dx 上被积函数的 2 253 形式不同． . 12

0

3
2
3
x2 1 练习：1.求曲线 y , y 与直线 x 3 2 1 x 2
x 3 所围成的图形的面积。
2.求曲线 xy 1 与直线
x y 0 y 2
x y 2
P1
2
所围成的图形的面积。 2014考研题
提示：1
P2
y
1
32 1 0 2 1 1 3 x 1 x 1 1 s 2[ ( )d x ( ( 3 3 2) ) d x ] 2 0 1 x 1 3 2 2 1 x2

高等数学(第三版)课件：定积分的应用

高等数学(第三版)课件：定积分的应用

线 y f ( x，) 直线 x a, x b (a b) 与
• x 轴围成的面积是在x 轴上方和下方曲边梯形
面积的差.
• • 同样可由微元法分析
•⒉ 一般地，根据微元法由曲线 y f ( x), y g( x),
• ( f ( x) g( x)) 及直线x a, x b 所围的图形
• 面积.（右图所示）
• 解: 取 为积分变量,
•
面积微元为
d
A
1 2
(a )2
d
• 于是
A 2 1 (a )2d a 2 2
02
23
2 4 a 2 3
03
• 例5 计算双纽线 r 2 a2 cos2 (a 0)
•
所围成的平面图形的面积（下图所示）
• 解 因 r 2 0,故 的变化范围是 [ 3 , 5 ,]
• ⑴分割区间[a,b],将所求量(曲边梯形面积 A )
分为部分量(小曲边梯形面积 Ai）之和;
• ⑵确定各部分量的近似值(小矩形面积);
Ai f (i )xi
• ⑶求和得所求量的近似值（各小矩形面积之和);
n
A f (i )xi
i 1
• ⑷对和式取极限得所求量的精确值（曲边梯形面积）.
n
A lim 0
• 它表示高为f ( x) 、底为 dx 的一个矩形面积.
• ⑵由定积分几何意义可知,当 f (x) 0 时,由曲
线 y f (x)，直线 x a, x b (a b) 与 x 轴所围成
的曲边梯形的面积A为
A
b
f (x)dx
.
a
• ⑶当 f ( x)在区间 [a, b]上的值有正有负时，则曲
•

高等数学第六章第二节定积分在几何学上的应用课件.ppt

高等数学第六章第二节定积分在几何学上的应用课件.ppt

解:
cos x 0,
2
x
2
s
2
2
2 2 0
1 y2 dx 1 ( cos x)2 dx
2 2
2 cos x dx
0
2
2
2
2
sin
x 2
2
0
4
的弧长.
例11. 计算摆线
一拱
的弧长 .
y
解: ds
(dd
x t
)2
(
d d
y t
)
2
d
t
o
a2 (1 cos t)2 a2 sin2 t d t
1 y2 dx
因此所求弧长
s b 1 y2 dx a
b
a
1 f 2(x) dx
y
y f (x)
ds
o a xxdxb x
(2) 曲线弧由参数方程给出:
弧长元素(弧微分) :
ds (dx)2 (dy)2
2 (t) 2 (t) dt
因此所求弧长
s
2 (t) 2 (t) d t
(3) 曲线弧由极坐标方程给出:
y b
o x ax
则 V 2 a y2 dx 0
(利用对称性)
2
b2 a2
a
(a
2
x2
)
dx
0
2
b2 a2
a2 x
1 3
x3
a 0
4 ab2
3
方法2 利用椭圆参数方程
则 V 20a y2 dx 2 ab2 sin3t d t
2 ab2 2 1
3
4 ab2
3
特别当b
=
a

《定积分课件》课件

《定积分课件》课件

03 定积分的应用
CHAPTER
面积与体积的计算
总结词
定积分在计算平面图形的面积和三维物体的体积方面具有广 泛应用。
详细描述
利用定积分，可以计算出由曲线围成的平面图形的面积，例 如由y=sinx和y=cosx围成的图形面积。此外，定积分还可以 用于计算三维物体的体积，例如球体、圆柱体和旋转体的体 积。
详细描述
在静水压力问题中，压力分布是深度的函数。通过定积分，我们可以计算任意 深度的压力分布，从而了解水下物体的受力情况。
引力场的强度
总结词
通过定积分计算引力场的强度，理解引 力场的分布规律。
VS
详细描述
在引力场中，场强是位置的函数。通过定 积分，我们可以计算任意位置的场强，从 而了解物体在引力场中的运动规律。
符号表示
02
定积分的符号为∫，读作“拉姆达”。
计算方法
03
定积分的计算方法是通过微积分基本定理，将定积分转化为求
原函数在某点的值。
定积分的几何意义
平面区域面积
定积分可以用来计算平面图形的面积，特别是 当面积元素与坐标轴平行时。
体积
定积分还可以用来计算三维物体的体积，例如 旋转体的体积。
曲线下面积
定积分可以用来计算曲线下在某一区间内的面积。
定积分的计算方法
要点一
总结词
定积分的计算方法包括直接法、换元法和分部积分法等。
要点二
详细描述
定积分的计算可以通过多种方法进行。直接法是根据微积 分基本定理，通过求原函数并计算其差值来得到定积分的 结果。换元法是在积分变量进行换元，使得积分简化。分 部积分法则是通过将两个函数的乘积进行积分，将一个积 分转化为另一个积分，从而简化计算。这些方法在计算定 积分时常常需要结合使用。

高中数学选修2-2定积分在几何中的应用课件

高中数学选修2-2定积分在几何中的应用课件

的交点为 (0, 0)
取x为积分变量, 则 x [0, 3].
所求的几何图形的面积表示为
A 3 ( x2 3x)dx 0
A 3 ( x2 3x)dx 9.
0
2
= 2
2
3
x2
3
4 0
+
2
2 3
3
x2
8 4
-
1 2
x-4 2
8 4
= 40 3
新知探究
例3
计算由曲线 y = x3 6x 和 y = x2 所围成的图形的面积.
首先画出草图，并设法把所求图形的面积问题转化为求两部分的面积问题.其次，确定被积函数 和积分的上、下限.
新知探究
由图可知，我们需要把所求图形的面积分成两部分 S1和S2 .需要求出曲线 y = x3 - 6x 、曲 线 y = x2 两个交点.
n
i =1 b
F = lim f λ →0 i=1
ξi Δxi =
f
a
x dx
新知探究
平面图形的面积 直角坐标系 设平面图形由上下两条曲线y=f上(x)与y=f下(x)及左右两 条直线x=a与x=b所围成.
新知探究
在点x处面积增量的近似值为 [f上(x)-f下(x)]dx, 它也就是面积元素. 因此平面图形的面积为
极坐标方程的情形
设由曲线 r = φθ 及射线 θ = α、θ = β 围成一曲边扇形， 求其面积.这里 φθ 在 α，β 上连续，且 φθ≥0 .
曲边扇形面积元素 dA = 1 [φ(θ)]2 dθ 2
d
r ( )
d
曲边扇形的面积公式 A = β 1[j(θ)]2 dθ. α2
o x

1.7定积分的几何应用

1.7定积分的几何应用

2
2
围成图形的面积.
解:作出y2=x,y=x2的图象如图所示:
解方程组 x 0 x 1 y x 或 2 y 0 y 1 y x
y
y
y xx
2
B
2
即两曲线的交点为(0,0),(1,1)
S = S曲 边 梯 形 OABC - S曲 边 梯 形 OABD
B(1，－ 1)． ∴围成图形 (阴影部分 )面积为
S＝
-2
1
(－ x2－ x＋ 2)dx 9 ＝ . 2
1 3 1 2 ＝ (－ x － x ＋ 2x) 3 2
9 答案： (1) 2
例 2 计算由曲线 y 围成的图形的面积.
2x
，直线 y
x 4 以及
y 2x
x 轴所
解:
两曲线的交点
2
|0 8
8
X型求解法
40 3
x 1 2 y
2
16 2 8
1 2
3
2

[( 4 y )
y ]d y
4
(4 y
44
1 2 1
2
y
2
2
1 6
x 4 y
y ) |0
1 6
3
4
4
40 3
Y型求解法
练习 1（例 2 变式题） ： 计算由曲线 y 2 x 和直线 y x 4 所围成的图形的面积
2π 4 A. B. 5 3 3 π C. D. 2 2 解析：选 B.由图象可知二次函数的表达式为 f(x)＝ 1－ x2，∴ S＝ 1 3 1 1 4 1 2 ＝ (1－ )－(－ 1＋ )＝ . -1 (1－ x )dx＝ (x－3x ) 3 3 3

《高中定积分的应用》课件

《高中定积分的应用》课件
总结词
定积分在计算曲线形状的质量分布方面具有广泛应用，有助于理解物体的重心和转动惯量等物理量。
详细描述
对于曲线形状的物体，我们可以通过定积分计算其质量分布，进而求出物体的重心和转动惯量。这对于分析物体 的稳定性和运动特性具有重要意义。
电场强度与电势的计算
总结词
在电场分析中，定积分用于计算电场强度和电势，有助于深入理解电场的性质和分布。
详细描述
在解决涉及多个函数的定积分问题时，需要仔细分析这 些函数之间的关系，如一个函数可能对另一个函数求导 或积分，或者两个函数之间存在特定的关系等。
复杂几何形状的分析与计算
总结词
对复杂几何形状的深入分析是解决问题的必要步骤。
详细描述
在解决涉及复杂几何形状的定积分问题时，需要深入理 解几何形状的特点，如面积、体积等，并能够运用适当 的公式进行计算。同时，还需要理解如何将复杂的几何 形状分解为更简单的部分，以便于解决定积分问题。
详细描述
在经济学中，边际分析通过计算边际成本、 边际收益和边际利润等指标，帮助企业决策 者判断生产、定价和销售等方面的最优策略 。弹性分析则通过计算需求价格弹性、供给 价格弹性等指标，分析市场价格的变动对需 求和供给的影响，进而影响市场均衡和资源 配置。
成本与收益计算
总结词
成本与收益计算是经济学中重要的财务分析 工具，用于评估企业的经营绩效和投资回报 。
THANK YOU
定积分的几何意义
总结词
定积分的几何意义有助于直观理解定积分的应用。
详细描述
定积分的几何意义表示一个曲线下的面积。通过计算定积分，可以求出曲线下某 个区间上的面积，从而解决一些实际问题，如求物体的质量、速度等。
定积分的计算方法

定积分的几何意义

定积分的几何意义

y
y f(x)=(x-1)2-1
f(x)=1
0a
①
x -10 2
②
x a 0 b x -10 2 x
③
④
解：（4）在图④中，被积 f (x)函(数 x1)2 1在[1， 2]
上连续，且 [1， 在 0]上f (x)0,在[0， 2]上f (x)0， 根据定积分的几何 可意 得义 阴影部分的面积
A 0 1 [x (1 ) 2 1 ] d x 0 2 [x (1 ) 2 1 ] dx
y
f(x)=x2
y
f(x)=x2
y
y f(x)=(x-1)2-1
f(x)=1
0a
①
x -10 2
②
x a 0 b x -10 2 x
③
④
解：（3）在图③中，被积f (函 x) 数1在[a，b]
上连续，f且 (x) 0,根据定积分的几何意
义，可得阴影部分积的为面A badx
y
f(x)=x2
y
f(x)=x2
的代数和表示 几何意义
4.应用
例1.用定积分表示图中四个阴影部分面积
y
f(x)=x2
y
f(x)=x2
y
y f(x)=(x-1)2-1
f(x)=1
0 a x -10 2 x a 0 b x -10 2 x
①பைடு நூலகம்
②
③
④
解：（1）在图①中，被积f (函 x) 数x2在[0，a]
上连续，f且 (x) 0,根据定积分的几何意
例2：
利用定积分的 说几 明何 等 2意 式 sin义 xdx0 2
成立。
y
解：在右图中，被积函数 f (x) sin x

定积分在几何上的应用

定积分在几何上的应用
0
2
a
y x2 y 2 2 1 2 b a b
4ab sin tdt ab.
2 0
2019/4/7 第六章 定积分的应用
2
o
图6-2-5
a x
8
2.极坐标情形
设由曲线 ( ) 及射线
d
()
d 、 围成一曲边扇 ( ) 形，求其面积．这里， 在[ , ]上连续，且 ( ) 0 ． 1 o 面积元素 dA [ ( )]2 d x 2 图6-2-6
3
a
o
a x
旋转体的体积
V a x a
2 3
图6-2-12
2019/4/7
第六章 定积分的应用
32 3 dx a . 105
16
类似地，如果旋转体是由连续曲线
x ( y ) 、直线 y c 、 y d 及y 轴所围 成的曲边梯形绕y 轴旋转一周而成的立体，
第六章 定积分的应用
1
b
例 1 计算由两条抛物线y 2 x 和 y x 2 所围成的 图形的面积.
解
两曲线的交点
(0,0) (1,1)
选 x 为积分变量 x [0,1]
面积元素 dA ( x x 2 )dx
2 3 x 1 2 A 0 ( x x )dx x . 3 0 3 3
R 2 2
1 2 R x dx R h. 2
23
第六章 定积分的应用
三、平面曲线的弧长
设 A、 B 是曲线弧上的两 个端点，在弧上插入分点
y
M2
M1
A M0
M n1

高中数学(新课标)选修2课件1.7.1-2定积分的应用

高中数学(新课标)选修2课件1.7.1-2定积分的应用

a
a
＝b[f(x)－g(x)]dx.
a
③如图(6)所示，所求面积 S＝S1＋S2＝ac[f(x)－g(x)]dx＋cb[g(x)－f(x)]dx
＝b|f(x)－g(x)|dx.
a
知识点二 定积分在物理中的应用 1．变速直线运动的路程 我们知道，做变速直线运动的物体所经过的路程 s，等于其速 度 函数 v＝ v(t)(v(t)≥0)在 时间 区间 [a， b] 上的定 积分 ，即 s ＝ ____b_v_(_t)_d_t ___.
【解析】 (1)由 v(t)＝8t－2t2≥0 得 0≤t≤4，即当 0≤t≤4 时， P 点向 x 轴正方向运动，t>4 时，P 点向 x 轴负方向运动．
故 t＝3 时，点 P 离开原点的路程
s1＝03(8t－2t2)dt＝4t2－23t330 ＝18. (2)当 t＝5 时，点 P 离开原点的位移 s2＝5(8t－2t2)dt
解析：由题意 v＝x′＝8t，t＝12 x，所以 v＝4 x.
又 F＝kv(k 是比例系数)，且当 v＝10 米/秒时 F＝2 牛，
所以 2＝10k，所以 k＝15，所以 F＝45 x，
又 F 与物体运动的方向相反，
所以 W＝－245 0
xdx＝－185x3220
＝－1165
2(焦耳)．
所以物体从 x＝0 到 x＝2 阻力所做的功为－1165 2焦耳．
解得 t＝0 或 t＝6，
t＝0 对应于 P 点刚开始从原点出发的情况，
∴t＝6 是所求的值．
状元随笔 首先要确定的是所需求的是路程还是位移，然后 用相应的方法求解．
方法归纳
(1)用定积分解决变速直线运动的位移和路程问题时，将物理问 题转化为数学问题是关键．

《定积分的简单应用》课件讲解学习

《定积分的简单应用》课件讲解学习

0
[解析] v＝ddxt＝(bt3)′＝3bt2， 媒质阻力F阻＝kv2＝k(3bt2)2＝9kb2t4，其中k为比例常
数，k>0.
当x＝0时，t＝0，当x＝a时，t＝ab13，
ds＝vdt，故阻力做的功为W阻＝
t
kv2·vdt＝k
t
v3dt＝k
t
0
0
0
(3bt2)3dt＝277k3 a7b2.
• [点评] 本题常见的错误是在计算所做的功 时，误将W阻＝∫t10F阻ds写为∫t10F阻dt.
(1)P从原点出发，当t＝6时，求点P离开原点 的路程和位移；
(2)P从原点出发，经过时间t后又返回原点时 的t值．
• [解析] (1)由v(t)＝8t－t2≥0得0≤t≤4， • 即当0≤t≤4时，P点向x轴正方向运动， • 当t>4时，P点向x轴负方向运动． • 故t＝6时，点P离开原点的路程
对于已知运动规律求做功的问题，首先确定其运动速 度，进而由 ds＝vdt 来确定做功的积分式 W＝t Fvdt.
0
6．已知自由落体的速率v＝gt，则落体从t＝ 0到tA＝.13gt0t20所走的路程为B（．gt20 )
C.12gt20
D.16gt20
[答案] C
[解析] 如果变速直线运动的速度为v＝v(t)(v(t)≥0)，
那么从时刻t＝a到t＝b所经过的路程是bv(t)dt， a
∴
＝12gt2t00 ＝12g(t20－0)＝12gt02.故应选C.
7．如果1N能拉长弹簧1cm，为了将弹簧拉 长6cm，所耗费的功为
()
A．0.18J
B．0.26J
C．0.12J
D．0.28J
[答案] A

6.定积分的几何应用

6.定积分的几何应用

x + dx b
x
小切线段的长 (dx )2 + (dy )2 = 1 + y′ 2 dx
′ 2 dx 弧长 s = 弧长元素 ds = 1 + y 1 + y′ 2 dx . ∫
b a
2 3 例 7 计算曲线 y = x 2 上相应于 x 从 a 到 b 3
的一段弧的长度. 的一段弧的长度
解
∵ y′ = x ,
2 2
的面积.
解 由对称性知总面 积=4倍第一象限 倍第一象限 部分面积
A = 4A1
y= x
ρ 2 = a 2 cos 2θ
1 2 A = 4∫0 a cos2θdθ = a2 . 2
4
π
例 6 求心形线r = a (1 + cos θ )所围平面图形的 面积 (a > 0).
解
dθ
1 2 2 dA= a (1+ cos ) dθ θ 2
2π
的周长. ( 0 ≤ t ≤ 2π) 的周长
s1 = ∫ =∫
0
0
′ 2 dx 1+ y 1 + a 2 cos 2 xdx 1 + a cos xdx ,
2 2
2π
= 2∫
π
0
设椭圆的周长为 s2
s2 =
∫0
π
π
2π
(x ′ )
2
2
+ ( y ′ ) dt ,
2
根据椭圆的对称性知
s2 = 2∫
x = r (θ ) cosθ ∵ y = r (θ ) sinθ
2 2
(α ≤ θ ≤ β )
= r 2 (θ ) + r ′ 2 (θ )dθ , ∴ ds = (dx ) + (dy )

大一上 高数A 定积分的几何应用

大一上 高数A 定积分的几何应用

x = b 所围成。 所围成。
bdx
面积表示为定积分的步骤如下
） 的小区间， （1）把区间[a , b]分成n 个长度为 ∆x i 的小区间， 个小窄曲边梯形， 相应的曲边梯形被分为n 个小窄曲边梯形， i 第 小窄曲边梯形的面积为∆Ai ，则 A = ∑ ∆Ai .
三、某些立体的体积
1. 平行截面面积为已知的立体的体积 已知平行截面面积为 A(x)的立体 dV=A(x)dx 的立体
.
V =
∫
b
a
A ( x )d x
A(x)
a
x
V
V =
b
x
已知平行截面面积为 A(y)的立体 的立体
∫
d
c
A ( y )d x
半径为R的正圆柱体被通过其底的直径并与底面成 例7. 半径为 的正圆柱体被通过其底的直径并与底面成α角的 平面所截，得一圆柱楔。求其体积。 平面所截，得一圆柱楔。求其体积。
1
3
1
2
例 2
计算由曲线 y = x 3 − 6 x 和 y = x 2 所围成
y = x3 − 6x
的图形的面积. 的图形的面积
解 两曲线的交点
y = x3 − 6x y = x2
⇒ (0,0), ( −2,4), ( 3,9).
y = x2
− 选 x 为积分变量 x ∈ [−2, 3] (1) x ∈ [−2, 0], dA1 = ( x 3 − 6 x − x 2 )dx ( 2) x ∈ [0,3], dA2 = ( x 2 − x 3 + 6 x )dx
o a x x + dx x b
） （1）U 是与一个变量 x 的变化区间[a, b ]有关 的量； 的量；

2022版高中数学第一章导数及其应用1.7.1定积分在几何中的应用课件新人教A版选修2_2

2022版高中数学第一章导数及其应用1.7.1定积分在几何中的应用课件新人教A版选修2_2
形AOB-S△ABC,
0
0
S 曲边三角形 AOB=
1
1

1
2 dx= 3 3 |0 0 = 3 03 .
1
S△ABC= 2 |||| = 2 0 1
1
1
3
4
12
则 S= 03 − 03 =
03 =
0
2
1
12
1
02 = 4 03 ,
,
解得x0=1,从而切点为A(1,1),切线方程为y=2x-1.
1
(1)由 S1=S2,得 3 3 = 3 3 - 2 + 3 , 解得 3 = 3.
∵0<t<1,
∴t=
3
3
.
∴当 t=
3
3
时,使 S1=S2.
1 3 3
-
3
典例透析
题型一
题型三
题型二
题型四
4
1
(2)由 S=S1+S2,得 S=S(t) = 3 3 - 2 + 3,0<t<1,
区间段内位于上方和下方的函数有所变化,通过解方程组求出曲线
的不同的交点坐标,可以将积分区间进展分解细化,然后根据图象
对各个区间分别求面积进而求和,在每个区间上被积函数均是由上
减下.
典例透析
题型一
题型二
题型三
题型四
【变式训练2】 求由曲线y=x2,直线y=x,y=3x围成的图形的面积
S.
解:在同一平面直角坐标系中作出曲线y=x2,直线y=x,y=3x的图
(1)求t的值,使S1=S2;
(2)求t的值,使S=S1+S2最小.
分析:应先根据题意及用定积分求曲边多边形面积的方法得出用
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
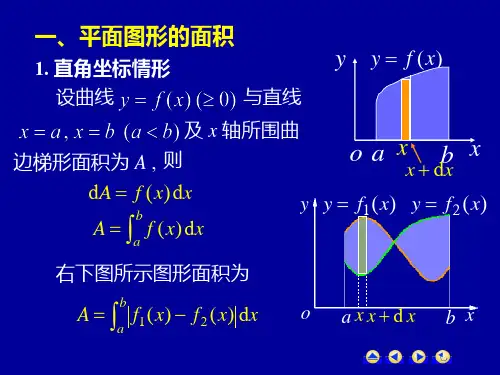
S= b (f (x) g(x))dx. a
思考：如何利用定积分表示上图2平面图形ABCD的面积？
提示：选取y为积分变量，积分区间为［a,b］，则图中平面
图形ABCD的面积为S
b
a (f2 (y) f1(y))dy.
【知识点拨】
1.定积分与各个小曲边梯形面积的关系
如果f(x)在［a,b］上有时取正值，
有时取负值时，且直线x=a,x=b,y=0
与曲线y=f(x)围成的各个小曲边梯形
的面积S1,S2,S3，那么f(x)在积分区间［a,b］上的定积分等
于这些小曲边梯形面积的代数和，即有
b
a f
(x)dx
S1
S2
S3.
2.对于不规则平面图形面积的求法 定积分只能用于求曲边梯形的面积，对于非规则的曲边梯形， 一般要将其分割或补形为规则的曲边梯形，再利用定积分的 和与差求面积.对于分割或补形中的多边形的面积，可直接利 用相关面积公式求解.
y y
及x ,
1x 3
x y 2,
y
1 3
x
得交点(1,1)，(0,0)，(3，-1),
所围图形如图中阴影部分所示，
所以
S＝
1
[
x ( 1 x)]dx
3
[(2
x
)
(
1
x)]dx
0
3
1
3
＝
1
(
x 1 x)dx
3(2 x 1 x)dx
0
3
1
3
＝( 2 3
3
x2
1 6
x2)
10
4
【误区警示】
【防范措施】 1.求被积函数f(x)与函数F(x)是计算定积分的关键 当图象为折线时，对应的函数为分段函数，要分别来求.本例 主要考查由分段函数的图象求函数式，考查定积分在计算平 面图形面积中的运用.突出体现数形结合思想以及计算能力， 求出被积函数f(x)以及函数F(x)的解析式是关键.
且与y轴垂直，则l与C所围成的图形的面积等于( )
A. 4
B.2
C. 8
D.16 2
3
3
3
【解析】选C.l的方程是y=1，所求面积相当于一个矩形面积
减去一个积分值：S
42
2 0
x2 dx
4
4 2( x3 12
02 )
8. 3
定积分在几何中的应用
定积分与平面图形面积的关系 1.已知函数f(x)在［a,b］上是连续函数，由直线y=0, x=a,x=b与曲线y=f(x)围成的曲边梯形的面积为S,填表：
f(x)的符号 f(x)≥0 f(x)<0
平面图形的面积与定积分的关系
b
S= a f (x)dx
b
S= a f (x)dx
2.一般地，如图1，如果在公共的积分区间［a,b］上有 f(x)＞g(x),那么直线x=a,x=b与曲线y=f(x),y=g(x)围成的 平面图形的面积为
1
4
S 20 xdx 1 ( x x 2)dx
2
2 3
3
x2
10
( 2 3
3
x2
1 2
x2
2x)
14
2
2
[( 2
3
42
1
42
2 4)
(2
1
2)]
33
2
32
9. 2
【拓展提升】求平面图形面积的步骤以及注意事项 (1)步骤：①画函数的图象，联立方程组求出曲线的交点坐标. ②将曲边形的面积转化为曲边梯形的面积. ③确定被积函数和积分区间，计算定积分，求出面积. (2)注意事项：根据图形特点选择适当的积分变量：若公共积 分区间在x轴上，选取x为积分变量；若公共积分区间在y轴上， 选取y为积分变量，要把函数变形成用y表示x的函数.
积，即 S a［b f1(x) (f其2 (中x)］fd1x(x)＞f2(x)).
类型 二 计算复杂平面图形的面积 【典型例题】 1.由两条曲线y=x2, y 1 x2与直线y=1围成平面区域的面积
4
是_______.
2.求曲线 y x 与直线y=2-x，y 1 x 围成图形的面积.
3
【解题探究】1.题1中怎样确定积分变量的区间？ 2.如何将图形的面积转化为定积分计算？ 探究提示： 1.由直线y=1分别与曲线y=x2y, 1 x联2 立，求出交点坐标，
(2x
1 2
x2
1 6
x2)
13
＝2 3
1 6
(2x
1 3
x2
)
13
＝5 6 1 9 21 1 1＝2 1 .
63
36
【互动探究】若将题2中条件变为如图由直线y=x-2，曲线 y2=x所围成图形，试求其面积S.
【解析】由
y2
x得, x=1或x=4,
y x 2,
故A(1,-1),B(4,2),如图所示:
【解析】1.直线y=0,x=1,x=4,曲线y x围成平面图形的面
积为 4 1
xdx
2 3
3
x2
|14
2 3
3
42
2 3
2 3
8
2 3
14 . 3
答案：14
3
2.由
y y
2x消x2 ,去3 y，得x2-2x-3=0，解得x1=-1,x2=3，这是
直线与抛物线交点的横坐标，如图，直线y=2x与抛物线
y=x2-3围成平面图形的面积是
S ［3 2x (x2 3)］dx 3 (3 2x x2 )dx
1
1
(3x
x2
1 3
x3
31
(3 3 32 1 33) [1 3 (1)2 1 (1)3]
3
3
9 2 1 32 . 33
【拓展提升】求函数图象围成平面图形面积的方法 (1)画出两个函数的图象，先将两个函数方程联立方程组求 解，得到函数图象的交点的横坐标a,b(a＜b)，确定积分区间 ［a,b］. (2)在公共的积分区间上，由上界函数减去下界函数作为被积 函数，定积分的值就等于两个函数图象围成平面图形的面
4
得出积分变量的区间. 2.灵活确定积分变量与积分区间，转化为定积分计算.
【解析】1.如图，y=1与y=x2交点A(1,1),y=1与y x2交点
4
B(2,1),由对称性可知面积
S=2( 1x2dx
2
dx
2 1x2dx) 4 .
0
1
04
3
答案：4
3
2.解方程组：y 及x ,
x y 2
类型 一 计算简单平面图形的面积 【典型例题】 1.直线y=0,x=1,x=4,曲线 y x 围成平面图形的面积为_____. 2.求直线y=2x与抛物线y=x2-3围成平面图形的面积是多少？
【解题探究】1.定积分的几何意义是什么？ 2.用积分求两曲线围成平面图形的面积时，如何确定积分上 限与下限？ 探究提示： 1.在积分区间上当被积函数值非负时，定积分等于曲边梯形 的面积. 2.将直线方程与抛物线方程联立方程组求出交点的横坐标即 为积分上下限，将平面图形的面积转化为定积分计算.
2.利用定积分性质与微积分基本定理是重点 当被积函数为分段函数，要充分利用定积分的性质及微积分 定理.本例考查了定积分的性质以及微积分基本定理等知识， 综合性强，计算量大，稍有不慎就会导致计算出错，解题时 要写出详细步骤，计算要耐心细致，一气呵成，考场上力争 避免“会而不对”等错误的发生.
【类题试解】(2013·北京高考)直线l过抛物线C:x2=4y的焦点
从而得
y
xf (x)
10x2,0Fra bibliotekx1 2
,
10x
10x
2
,
1 2
＜x
1,
①
所以所求的面积为 S
1
210x2dx
0
1 1
(10x
10x
2
)dx
2
10 x3 3
1 2
(5x 2
10
x3)
0
3
1 1 2
②
=10 1 (5 10) (5 10 1) 5 .
38
3 4 38 4
答案：5
【易错误区】因忽视被积函数以及原函数导致计算错误
【典例】(2012·上海高考)已知函数y=f(x)的图象是折线段
ABC，其中A(0,0),B( 1 ,5),C(1,0)，函数y=xf(x)(0≤x≤1)
2
的图象与x轴围成的图形的面积为______.
【解析】根据题意，得 f (x) 1100x,100x,x12＜12x, 1, ①