小学三角形知识点及配套练习题图文稿
- 格式:docx
- 大小:255.67 KB
- 文档页数:6

【三角形】1、三角形的定义:由三条线段围成的图形(每相邻两条线段的端点相连或重合),叫三角形。
2、从三角形的一个顶点到它的对边做一条垂线,顶点和垂足间的线段叫做三角形的高,这条对边叫做三角形的底。
三角形只有 3 条高。
重点:三角形高的画法。
3、三角形的特性: 1、物理特性:稳定性。
如:自行车的三角架,电线杆上的三角架。
4、边的特性:任意两边之和大于第三边。
5、为了表达方便,用字母A、B、C 分别表示三角形的三个顶点,三角形可表示成三角形 ABC。
6、三角形的分类:按照角大小来分:锐角三角形,直角三角形,钝角三角形。
按照边长短来分:等边三角形、等腰三角形、三条边都不相等的三角形7、三个角都是锐角的三角形叫做锐角三角形。
8、有一个角是直角的三角形叫做直角三角形。
(其他两个角必定是锐角)9、有一个角是钝角的三角形叫做钝角三角形。
(其他两个角比定是锐角)10、每个三角形都至少有两个锐角;每个三角形都至多有 1 个直角;每个三角形都至多有 1 个钝角。
11、两条边相等的三角形叫做等腰三角形。
(等腰三角形的特点:两腰相等,两个底角相等)12、三条边都相等的三角形叫等边三角形(正三角形)(等边△的三边相等,每个角是60 度)13、等边三角形是特殊的等腰三角形14、三角形的内角和等于180°;四边形的内角和是360°;五边形的内角和是540 °15、图形的拼组:用任意 2 个完全一样的三角形一定能拼成一个平行四边形。
16、用 2 个相同的三角形可以拼成一个平行四边形。
17、用 2 个相同的直角三角形可以拼成一个长方形、一个平行四边形、一个大等腰三角形。
18、用 2 个相同的等腰直角的三角形可以拼成一个正方形、一个平行四边形、一个大的等腰的直角的三角形。
19、密铺:可以进行密铺的图形有长方形、正方形、三角形以及正六边形等。
课堂巩固练习一、用心选一选。
1、一个三角形有()条高。
A、1B、3 C 、无数2、如果直角三角形的一个锐角是A、20° B 、 70°20°,那么另一个角一定是(C、 160°)。
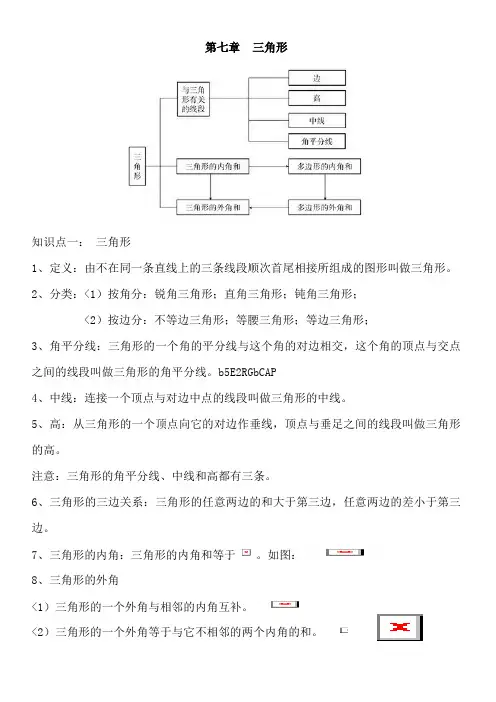
第七章三角形知识点一:三角形1、定义:由不在同一条直线上的三条线段顺次首尾相接所组成的图形叫做三角形。
2、分类:<1)按角分:锐角三角形;直角三角形;钝角三角形;<2)按边分:不等边三角形;等腰三角形;等边三角形;3、角平分线:三角形的一个角的平分线与这个角的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
b5E2RGbCAP4、中线:连接一个顶点与对边中点的线段叫做三角形的中线。
5、高:从三角形的一个顶点向它的对边作垂线,顶点与垂足之间的线段叫做三角形的高。
注意:三角形的角平分线、中线和高都有三条。
6、三角形的三边关系:三角形的任意两边的和大于第三边,任意两边的差小于第三边。
7、三角形的内角:三角形的内角和等于。
如图:8、三角形的外角<1)三角形的一个外角与相邻的内角互补。
<2)三角形的一个外角等于与它不相邻的两个内角的和。
<3)三角形的一个外角大于任何一个与它不相邻的内角。
>或>6、三角形的周长、面积求法和三角形稳定性。
<1)如图1:C△ABC=AB+BC+AC或C△ABC= a+b+c。
四个量中已知其中三个能求第四个。
<2)如图2:AD为高,S△ABC=·BC·AD三个量中已知其中两个能求第三个。
<3)如图3:△ABC中,∠ACB=90°,CD为AB边上的高,则有:S△ABC=·AB·CD=·AC·BC即:AB·CD=AC·BC四条线段中已知其中三条能求第四条。
知识点二:多边形及其内角和1、边形的内角和=;2、边形的外角和=。
3、一个边形的对角线有条,过边形一个顶点能作出条对角线,把边形分成了个三角形。
例题讲解例 1.如图,为估计池塘岸边的距离,小方在池塘的一侧选取一点,测得M,=10M,间的距离不可能是< )p1EanqFDPwA.20MB.15MC.10MD.5M例2已知一个多边形的内角和与某个外角的度数的总和为1350°,求这个多边形的边数.例3 若一个多边形有77条对角线,求它的内角和.例4 下列各组三条线段中,不能组成三角形的是< )。

人教版小学五年级上册第六章三角形的
内角和知识点及习题
人教版小学五年级上册第六章三角形的内角和知识
点及题
知识点
- 了解三角形的内角是180度的特点
- 掌握计算三角形内角和的方法
- 理解三角形内角和与三角形形状之间的关系
题
1. 用已知角度计算三角形内角和:
- 已知一个角为60度,另一个角为40度,求第三个角的度数。
- 已知一个角为90度,另一个角为30度,求第三个角的度数。
- 已知两个角分别为80度和60度,求第三个角的度数。
2. 判断下列三角形的内角和是否等于180度:
- 一个角为120度,另外两个角分别为20度和40度。
- 一个角为60度,另外两个角分别为60度和60度。
- 一个角为45度,另外两个角分别为45度和90度。
3. 运用三角形内角和的知识,解决下列问题:
- 一个三角形的两个角度分别为30度和75度,求第三个角度的度数。
- 一个三角形的两个角度分别为60度和70度,求第三个角度的度数。
4. 根据三角形内角和的性质,选择填空:
- 一个三角形的一个角为45度,另一个角为35度,那么第三个角一定是( 100 / 110 / 120 / 130 )度。
- 一个三角形的两个角度分别为50度和70度,那么第三个角一定是( 50 / 60 / 70 / 80 )度。
注意事项
- 计算三角形内角和时,只需将已知的角度相加即可。
- 三角形的内角和一定等于180度,如果计算的结果不等于180度,那么可能存在错误。
- 通过观察三角形的形状,可以对三个角的度数进行估算和推断。




三角形章节复习全章知识点梳理:一、三角形基本概念1. 三角形的概念由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。
2.3. 三角形三边的关系(重点)三角形的任意两边之和大于第三边。
三角形的任意两边之差小于第三边。
(这两个条件满足其中一个即可)用数学表达式表达就是:记三角形三边长分别是a,b,c,则a+b>c或c-b<a。
已知三角形两边的长度分别为a,b,求第三边长度的范围:|a-b|<c<a+b解题方法:①数三角形的个数方法:分类,不要重复或者多余。
②给出三条线段的长度或者三条线段的比值,要求判断这三条线段能否组成三角形方法:最小边+较小边>最大边不用比较三遍,只需比较一遍即可③给出多条线段的长度,要求从中选择三条线段能够组成三角形方法:从所给线段的最大边入手,依次寻找较小边和最小边;直到找完为止,注意不要找重,也不要漏掉。
④已知三角形两边的长度分别为a,b,求第三边长度的范围方法:第三边长度的范围:|a-b|<c<a+b⑤给出等腰三角形的两边长度,要求等腰三角形的底边和腰的长方法:因为不知道这两边哪条边是底边,哪条边是腰,所以要分类讨论,讨论完后要写“综上”,将上面讨论的结果做个总结。
二、三角形的高、中线与角平分线1. 三角形的高从△ABC的顶点向它的对边BC所在的直线画垂线,垂足为D,那么线段AD叫做△ABC的边BC上的高。
三角形的三条高的交于一点,这一点叫做“三角形的垂心”。
2. 三角形的中线连接△ABC的顶点A和它所对的对边BC的中点D,所得的线段AD叫做△ABC的边BC上的中线。
三角形三条中线的交于一点,这一点叫做“三角形的重心”。
三角形的中线可以将三角形分为面积相等的两个小三角形。
3. 三角形的角平分线∠A的平分线与对边BC交于点D,那么线段AD叫做三角形的角平分线。
要区分三角形的“角平分线”与“角的平分线”,其区别是:三角形的角平分线是条线段;角的平分线是条射线。
三角形三条角平分线的交于一点,这一点叫做“三角形的内心”。

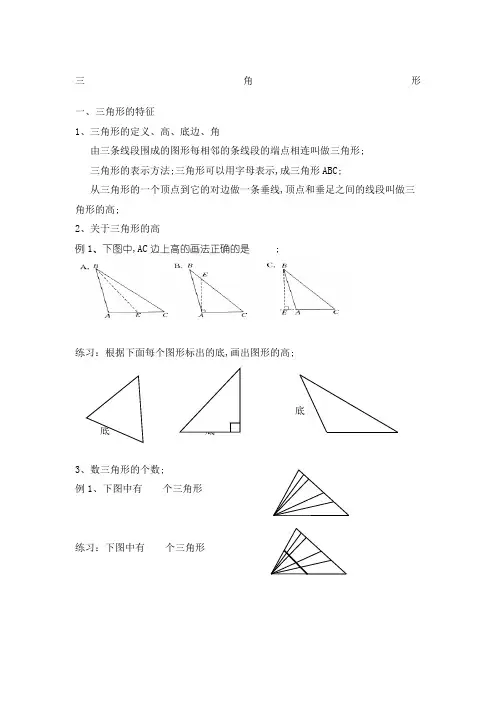
三角形一、三角形的特征1、三角形的定义、高、底边、角由三条线段围成的图形每相邻的条线段的端点相连叫做三角形;三角形的表示方法;三角形可以用字母表示,成三角形ABC;从三角形的一个顶点到它的对边做一条垂线,顶点和垂足之间的线段叫做三角形的高;2、关于三角形的高例1、下图中,AC边上高的画法正确的是 ;练习:根据下面每个图形标出的底,画出图形的高;底底底3、数三角形的个数;例1、下图中有个三角形练习:下图中有个三角形4、三角形的特性三角形具有稳定性,并在生活中被广泛应用;举例说明生活中的应用;二、三角形的分类1、三角形按角分类三角形可以分为锐角三角形,直角三角形和钝角三角形;因为在一个三角形至少有两个锐角,所以可以直角根据最大的角判断三角形的类型,最大的角是哪类角;例1、将下图分成三个三角形,它们可能是什么三角形你能想出哪些有分法例2、仔细填下列图;1、一个三角形里面最多有锐角,最少有个锐角;A、1B、2C、32、一个直角三角形中,最多有个锐角;A、1B、2C、33、在一个三角形中,有两个角都是60°,这是三角形;A、等边B、等腰C、直角4、如右图,一块三角形纸片被撕去了一个角;这个角是度,原来这块纸片的形状是三角形,也是三角形;2、三角形的内角和180°证明例1、求出下面图形中的角的度数;例2、一个等腰三角形的顶角是底角的4倍,这个等腰三角形的底角和顶角分别是多少度练习、1、求下面各角的度数,并指出它们是什么三角形1∠1=42°,∠2=38°,求∠3的度数;(2)∠1=28°,∠2=62°,求∠3的度数;(3)∠1=48°,∠2=62°,求∠3的度数;总结:对于任意一个三角形,至少都有两个锐角;这两个锐角之和一定要小于90°;判断一个三角形的形状要看它的最大角是什么角;2、求出下面图形中的角的度数;3、求这个正六边形的内角和是多少度3、解决问题;1公园的草坪里有一块等腰三角形的警示牌;警示牌的底角是多少度3、一个等腰三角形的顶角是底角的4倍,这个等腰三角形的底角和顶角分别是多少度 9分4、一根铁丝可以围成一个边长为3厘米的正方形,如果改围一个等边三角形,那么等边三角形的边长是多少厘米三、三角形的三边关系三角形按边分类:三角形任意两边的和大于第三边;为什么呢例1、下面三组小棒,不能围成三角形的是 ;例2、一个等腰三角形的一边是6cm,另一个边是3存煤,它的周长是 ;例3、如果三角形的两条边分别长4厘米和8厘米,另一条边可能是几厘米练习、 一根绳子长48厘米;1、如果用这根绳子围成一个底边长12厘米的等腰三角形,这个三角形的腰长是多少厘米2、如果用这根绳子围成一个边长18厘米的等腰三角形,这个三角形的腰长是多少厘米3、如果这根绳子围成一个等边三角形,这个等边三角形的边长是多少厘米3厘米 3厘米5厘米4厘米 4厘米 4厘米3厘米 3厘米6厘米5、图形的拼组:知识点一:三角形与四边形的关系;任何两个相同的三角形都可以拼成一个平行的四边形;两个相同的直角三角形可以拼成一个长方形平行四边形;两个相同的等腰三角形可以拼成一个正方形或平行四边形;三个相同的三角形可以拼成一个梯形;例1、把一个平行四边分割成一个等腰三角形和一个等腰梯形;课后作业一、判断题;1、由三条线段一定可以组成三角形;2、三角形两个内角和是115度,另一个角一定是75度;3、有一个钝角的三角形是钝角三角形 ;4、等腰三角形一定是锐角的三角形;5、等边三角形也是锐角三角形;6、有一个锐角的三角形是锐角的三角形;二、选择题;1、等腰三角形的一个底角是70度,那么顶角是 ;A、110度B、40度C、55度2、所有的等边三角形都是 ;A、直角三角形B、钝角三角形C、锐角三角形3、平行四边形的内角和是 ;A、180度B、270度C、360度4、三角形中有一个角是100°,这个三角形是A、锐角三角形B、钝角三角形C、直角三角形5、在一个三角形中,∠1=20°,∠2=40°,这是一个三角形;A、等边B、直角C、钝角D、锐角6、一个直角三角形中,最多有个锐角;A、1B、2C、37、在一个三角形中,有两个角都是60°,这是三角形;A、等边B、等腰C、直角8、任意一个三角形至少有个锐角;A、1B、2C、3三、解决问题;1、一个等腰三角形,有一个内角是70°,其他两个内角各是多少度2、一个等腰三角形有两个边分别是4厘米、9厘米,它的周长是多少厘米3、一个等腰三角形有两个边分别是4厘米、5厘米,它的周长是多少厘米。

第七章三角形【知识要点】一.认识三角形1.关于三角形的概念及其按角的分类定义:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
2.三角形的分类:①三角形按内角的大小分为三类:锐角三角形、直角三角形、钝角三角形。
②三角形按边分为两类:等腰三角形和不等边三角形。
2.关于三角形三条边的关系(判断三条线段能否构成三角形的方法、比较线段的长短)根据公理“两点之间,线段最短”可得:三角形任意两边之和大于第三边。
三角形任意两边之差小于第三边。
3.与三角形有关的线段..:三角形的角平分线、中线和高三角形的角平分线:三角形的一个角的平分线与对边相交形成的线段;三角形的中线:连接三角形的一个顶点与对边中点的线段,三角形任意一条中线将三角形分成面积相等的两个部分;三角形的高:过三角形的一个顶点做对边的垂线,这条垂线段叫做三角形的高。
注意:①三角形的角平分线、中线和高都是线段,不是直线,也不是射线;②任意一个三角形都有三条角平分线,三条中线和三条高;③任意一个三角形的三条角平分线、三条中线都在三角形的内部。
但三角形的高却有不同的位置:锐角三角形的三条高都在三角形的内部;直角三角形有一条高在三角形的内部,另两条高恰好是它两条直角边;钝角三角形一条高在三角形的内部,另两条高在三角形的外部。
④一个三角形中,三条中线交于一点,三条角平分线交于一点,三条高所在的直线交于一点。
(三角形的三条高(或三条高所在的直线)交与一点,锐角三角形高的交点在三角形的内部,直角三角形高的交点是直角顶点,钝角三角形高(所在的直线)的交点在三角形的外部。
)4.三角形的内角与外角(1)三角形的内角和:180°引申:①直角三角形的两个锐角互余;②一个三角形中至多有一个直角或一个钝角;③一个三角中至少有两个内角是锐角。
(2)三角形的外角和:360°(3)三角形外角的性质:①三角形的一个外角等于与它不相邻的两个内角的和;——常用来求角度②三角形的一个外角大于任何一个与它不相邻的内角。

【三角形】1、三角形的定义:由三条线段围成的图形(每相邻两条线段的端点相连或重合),叫三角形。
2、从三角形的一个顶点到它的对边做一条垂线,顶点和垂足间的线段叫做三角形的高,这条对边叫做三角形的底。
三角形只有3条高。
重点:三角形高的画法。
3、三角形的特性:1、物理特性:稳定性。
如:自行车的三角架,电线杆上的三角架。
4、边的特性:任意两边之和大于第三边。
5、为了表达方便,用字母A、B、C分别表示三角形的三个顶点,三角形可表示成三角形ABC。
6、三角形的分类:按照角大小来分:锐角三角形,直角三角形,钝角三角形。
按照边长短来分:等边三角形、等腰三角形、三条边都不相等的三角形7、三个角都是锐角的三角形叫做锐角三角形。
8、有一个角是直角的三角形叫做直角三角形。
(其他两个角必定是锐角)9、有一个角是钝角的三角形叫做钝角三角形。
(其他两个角比定是锐角)10、每个三角形都至少有两个锐角;每个三角形都至多有1个直角;每个三角形都至多有1个钝角。
11、两条边相等的三角形叫做等腰三角形。
(等腰三角形的特点:两腰相等,两个底角相等)12、三条边都相等的三角形叫等边三角形(正三角形) (等边△的三边相等,每个角是60度)13、等边三角形是特殊的等腰三角形14、三角形的内角和等于180°;四边形的内角和是360°;五边形的内角和是540°15、图形的拼组:用任意2个完全一样的三角形一定能拼成一个平行四边形。
16、用2个相同的三角形可以拼成一个平行四边形。
17、用2个相同的直角三角形可以拼成一个长方形、一个平行四边形、一个大等腰三角形。
18、用2个相同的等腰直角的三角形可以拼成一个正方形、一个平行四边形、一个大的等腰直角的三角形。
19、密铺:可以进行密铺的图形有长方形、正方形、三角形以及正六边形等。
课堂巩固练习一、用心选一选。
1、一个三角形有()条高。
A、1B、3C、无数2、如果直角三角形的一个锐角是20°,那么另一个角一定是()。
第27章:相似一、基础知识(一).比例1.第四比例项、比例中项、比例线段;2.比例性质:(1)基本性质:(2)合比定理:(3)等比定理:3.黄金分割:如图,若,则点P为线段AB的黄金分割点.4.平行线分线段成比例定理(二)相似1.定义:我们把具有相同形状的图形称为相似形.2.相似多边形的特性:相似多边的对应边成比例,对应角相等.3.相似三角形的判定(1)平行于三角形一边的直线与其它两边相交,所构成的三角形与原三角形相似。
(2)如果两个三角形的三组对应边的比相等,那么这两个三角形相似。
(3)如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
(4)如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。
4.相似三角形的性质(1)对应边的比相等,对应角相等.(2)相似三角形的周长比等于相似比.(3)相似三角形的面积比等于相似比的平方.(4)相似三角形的对应边上的高、中线、角平分线的比等于相似比.5.三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线.三角形中位线性质: 三角形的中位线平行于第三边,并且等于它的一半。
6.梯形的中位线定义:梯形两腰中点连线叫做梯形的中位线.梯形的中位线性质: 梯形的中位线平行于两底并且等于两底和的一半.7.相似三角形的应用:1、利用三角形相似,可证明角相等;线段成比例(或等积式);2、利用三角形相似,求线段的长等3、利用三角形相似,可以解决一些不能直接测量的物体的长度。
如求河的宽度、求建筑物的高度等。
(三)位似:位似:如果两个图形不仅是相似图形,而且是每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形。
这个点叫做位似中心.这时的相似比又称为位似比.位似性质:位似图形上任意一对对应点到位似中心的距离之比等于位似位似比二、经典例题例1.如图在4×4的正方形方格中,△ABC和△DEF的顶点都在长为1的小正方形顶点上.(1)填空:∠ABC=______,BC=_______.(2)判定△ABC与△DEF是否相似?[考点透视]本例主要是考查相似的判定及从图中获取信息的能力.[参考答案] ①135°,2 ②能判断△ABC与△DEF相似,∵∠ABC=∠DEF=135°,=【点评】注意从图中提取有效信息,再用两对应边的比相等且它们两夹角相等来判断.例2. 如图所示,D、E两点分别在△ABC两条边上,且DE与BC不平行,请填上一个你认为适合的条件_________,使得△ADE∽△ABC.[考点透视]本例主要是考查相似的判定[参考答案] ∠1=∠B或∠2=∠C,或点评:结合判定方法补充条件.例3. 如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走2米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度等于( )A.4.5米 B.6米 C.7.2米 D.8米[考点透视]本例主要是考查相似的应用[参考答案] B【点评】在解答相似三角形的有关问题时,遇到有公共边的两对相似三角形,往往会用到中介比,它是解题的桥梁,如该题中“”.例4. 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?[考点透视]本例主要是考查相似的实际应用[参考答案] 48mm【点评】解决有关三角形的内接正方形(或矩形)的计算问题,一般运用相似三角形“对应高之比等于相似比”这一性质来解答.例5.如图所示,在△ABC中,AB=AC=1,点D、E在直线BC上运动,设BD=x,CE=y.(1)如果∠BAC=30°,∠DAE=105°,试确定y与x之间的函数关系式;(2)如果∠BAC的度数为α,∠DAE的度数为β,当α、β满足怎样的关系式时,(1)中y与x之间的函数关系式还成立,试说明理由.[考点透视]本例主要是考查相似与函数的综合运用.[参考答案]解:在△ABC中,AB=AC=1,∠BAC=30°,∠ABC=∠ACB=75°,∠ABD=∠ACE=105°.又∠DAE=105°,∴∠DAB+∠CAE=75°.又∠DAB+∠ADB=∠ABC=75°,∴∠CAE=∠ADB,∴△ADB∽△EAC,∴,∴y=.当α1β满足β- =90°,y=仍成立.此时∠DAB+∠CAE=β-α,∴∠DAB+∠ADB=β-α,∴∠CAE=∠ADB.又∵∠ABD=∠ACE,∴△ADB∽△EAC,∴y=.【点评】确定两线段间的函数关系,可利用线段成比例、找相等关系转化为函数关系.例6. 一般的室外放映的电影胶片上每一个图片的规格为:3.5cm×3.5cm,放映的荧屏的规格为2m×2m,若放映机的光源距胶片20cm时,问荧屏应拉在离镜头多远的地方,放映的图象刚好布满整个荧屏?解析:胶片上的图象和荧屏上的图象是位似的,镜头就相当于位似中心,因此本题可以转化为位似问题解答.[考点透视]本例主要是考查位似的性质.[参考答案] m【点评】位似图形是特殊位置上的相似图形,因此位似图形具有相似图形的所有性质.三.适时训练(一)精心选一选1.梯形两底分别为m、n,过梯形的对角线的交点,引平行于底边的直线被两腰所截得的线段长为( )(A) (B) (C) (D)2.如图,在正三角形ABC中,D,E分别在AC,AB上,且=,AE=BE,则( )(A)△AED∽△BED(B)△AED∽△CBD(C)△AED∽△ABD(D)△BAD∽△BCD题2 题4 题53.P是Rt△ABC斜边BC上异于B、C的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的直线共有( )(A)1条 (B)2条 (C)3条 (D)4条4.如图,∠ABD=∠ACD,图中相似三角形的对数是( )(A)2 (B)3 (C)4 (D)55.如图,ABCD是正方形,E是CD的中点,P是BC边上的一点,下列条件中,不能推出△ABP与△ECP相似的是( )(A)∠APB=∠EPC (B)∠APE=90°(C)P是BC的中点(D)BP ︰BC=2︰36.如图,△ABC中,AD⊥BC于D,且有下列条件:(1)∠B+∠DAC=90°;(2)∠B=∠DAC;(3)=;(4)AB2=BD·BC其中一定能够判定△ABC是直角三角形的共有( )(A)3个 (B)2个 (C)1个 (D)0个题6 题7 题87.如图,将△ADE绕正方形ABCD顶点A顺时针旋转90°,得△ABF,连结EF交AB于H,则下列结论中错误的是( )(A)AE⊥AF (B)EF︰AF=︰1(C)AF2=FH·FE (D)FB ︰FC=HB︰EC8.如图,在矩形ABCD中,点E是AD上任意一点,则有( )(A)△ABE的周长+△CDE的周长=△BCE的周长(B)△ABE的面积+△CDE的面积=△BCE的面积(C)△ABE∽△DEC(D)△ABE∽△EBC9.如图,在□ABCD中,E为AD上一点,DE︰CE=2︰3,连结AE、BE、BD,且AE、BD交于点F,则S△DEF︰S△EBF︰S△ABF等于( )(A)4︰10︰25 (B)4︰9︰25 (C)2︰3︰5 (D)2︰5︰25题9 题10 题1110.如图,直线a∥b,AF︰FB=3︰5,BC︰CD=3︰1,则AE︰EC为( ).(A)5︰12 (B)9︰5 (C)12︰5 (D)3︰2 11.如图,在△ABC中,M是AC边中点,E是AB上一点,且AE=AB,连结EM并延长,交BC的延长线于D,此时BC︰CD为( )(A)2︰1 (B)3︰2 (C)3︰1 (D)5︰212.如图,矩形纸片ABCD的长AD=9 cm,宽AB=3 cm,将其折叠,使点D与点B重合,那么折叠后DE的长和折痕EF的长分别为( )(A)4 cm、cm (B)5 cm、cm(C)4 cm、2 cm (D)5 cm、2 cm题12(二)细心填一填13.已知线段a=6 cm,b=2 cm,则a、b、a+b的第四比例项是_____cm,a+b与a-b的比例中项是_____cm.14.若===-m2,则m=______.15.如图,在△ABC中,AB=AC=27,D在AC上,且BD=BC=18,DE∥BC交AB于E,则DE=_______.16.如图,□ABCD中,E是AB中点,F在AD上,且AF=FD,EF交AC于G,则AG︰AC=______.题16 题17 题1817.如图,AB∥CD,图中共有____对相似三角形.18.如图,已知△ABC,P是AB上一点,连结CP,要使△ACP∽△ABC,只需添加条件______(只要写出一种合适的条件).19.如图,AD是△ABC的角平分线,DE∥AC,EF∥BC,AB=15,AF =4,则DE的长等于________.题19 题20 题2120.如图,△ABC中,AB=AC,AD⊥BC于D,AE=EC,AD=18,BE =15,则△ABC的面积是______.21.如图,直角梯形ABCD中,AD∥BC,AC⊥AB,AD=8,BC=10,则梯形ABCD面积是_________.22.如图,已知AD∥EF∥BC,且AE=2EB,AD=8 cm,AD=8 cm,BC=14 cm,则S梯形AEFD︰S梯形BCFE=____________.(三)认真答一答23.方格纸中,每个小格的顶点叫做格点,以格点连线为边的三角形叫做格点三角形.请你在图示的10×10的方格纸中,画出两个相似但不全等的格点三角形,并加以证明(要求所画三角形是钝角三角形,并标明相应字母).24.如图,△ABC中,CD⊥AB于D,E为BC中点,延长AC、DE相交于点F,求证=.25.如图,在△ABC中,AB=AC,延长BC至D,使得CD=BC,CE⊥BD交AD于E,连结BE交AC于F,求证AF=FC.26.已知:如图,F是四边形ABCD对角线AC上一点,EF∥BC,FG∥AD.求证:+=1.27.如图,BD、CE分别是△ABC的两边上的高,过D作DG⊥BC于G,分别交CE及BA的延长线于F、H,求证:(1)DG2=BG·CG;(2)BG·CG=GF·GH.28.如图,∠ABC=∠CDB=90°,AC=a,BC=b.(1)当BD与a、b之间满足怎样的关系时,△ABC∽△CDB?(2)过A作BD的垂线,与DB的延长线交于点E,若△ABC∽△CDB.求证四边形AEDC为矩形(自己完成图形).29.如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连结FC(AB>AE).(1)△AEF与△EFC是否相似?若相似,证明你的结论;若不相似,请说明理由;(2)设=k,是否存在这样的k值,使得△AEF∽△BFC,若存在,证明你的结论并求出k的值;若不存在,说明理由.30.如图,在Rt△ABC中,∠C=90°,BC=6 cm,CA=8 cm,动点PC出发,以每秒2 cm的速度沿CA、AB运动到点B,则从C点出发多少秒时,可使S△BCP=S△ABC31. 如图,小华家(点A处)和公路(L)之间竖立着一块35m长且平 行于公路的巨型广告牌(DE).广告牌挡住了小华的视线,请在图中画出视点A的盲区,并将盲区内的那段公路设为BC.一辆以60km/h匀速行驶的汽车经过公路段BC的时间是3s,已知广告牌和公路的距离是40m,求小华家到公路的距离(精确到1m).32. 某老师上完“三角形相似的判定”后,出了如下一道思考题:如图所示,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,试问:△AOB和△DOC是否相似?某学生对上题作如下解答:答:△AOB∽△DOC.理由如下:在△AOB和△DOC中,∵AD∥BC,∴,∵∠AOB=∠DOC,∴△AOB∽△DOC.请你回答,该学生的解答是否正确?如果正确,请在每一步后面写出根据;如果不正确,请简要说明理由.33. 如图:四边形ABCD中,∠A=∠BCD=90°,①过C作对角线BD的垂线交BD、AD于点E、F,求证:;②如图:若过BD上另一点E作BD的垂线交BA、BC延长线于F、G,又有什么结论呢?你会证明吗?34.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.35. (1)如图一,等边△ABC中,D是AB上的动点,以CD为一边,向上作等边△EDC,连结AE。
四年级三角形的知识点总结及练习题一、三角形的定义在平面内,由三条不在一条直线上的线段连接成的图形叫做三角形。
二、三角形的分类三角形可以根据边长和角度的不同分为以下几种:1.根据边长分类(1)等边三角形三条边都相等的三角形,也叫正三角形。
(2)等腰三角形至少有两条边相等的三角形,其中相等的两边成为两腰,两腰之间的夹角叫做顶角。
(3)普通三角形三条边都不相等的三角形。
2.根据角度分类(1)锐角三角形三个角都小于90度的三角形。
(2)直角三角形三角形中有一个90度的角,这个角所对的边叫做斜边,另外两个角和边分别叫做直角和直角边。
(3)钝角三角形三个角中有一个角大于90度的三角形。
三、三角形的性质1.角的性质三角形的三个内角一定相加等于180度。
2.边的性质(1)任何一条边都小于其它两边之和。
(2)任何一条边都大于其它两边之差。
(3)两边之和大于第三边。
四、三角形的面积1.海龙公式当已知三角形的三边长a、b、c时,海龙公式计算三角形的面积S:s = (a+b+c)/2S = sqrt(s(s-a)(s-b)(s-c))2.高度公式当已知三角形的底边长b和高度h时,高度公式计算三角形的面积S:S = 1/2 * b * h五、练习题1.判断下列各图形是否为三角形。
image1解答:不是三角形,三条线段不在同一平面内。
2.判断下列各图形是否为等边三角形。
image2解答:不是等边三角形,两边长度不相等。
3.已知三角形的三边长分别为3cm、4cm和5cm,求其面积。
解答:s = (a+b+c)/2 = (3+4+5)/2 = 6S = sqrt(s(s-a)(s-b)(s-c)) = sqrt(632*1) = 3√6 所以该三角形面积为3√6(cm²)。
4.已知三角形的底边长为6cm,高度为4cm,求其面积。
解答: S = 1/2 * b * h = 1/2 * 6 * 4 = 12 所以该三角形面积为12(cm²)。
小学四年级数学三角形的分类(知识点梳理+典型例题)------------------------------------------作者xxxx------------------------------------------日期xxxx三角形的相关概念考点一【三角形的特性】三角形的定义:由三条线段围成的图形(每相邻两条线段的端点相连)叫做三角形三角形的高:从三角形的一个顶点到它的对边做一条垂线,顶点和垂足之间的线段三角形的底: 这条对边叫做三角形的底三角形的性质:①物理特性:三角形具有稳定性(不易变形)②三边的特性:三角形任意两边的和大于第三边知识典例题型一:画出三角形的底边上的高例1:画出下面每个三角形底边上的高.例2:画三条不同的高题型二:三角形的内角和用字母A、B、C分别表示三角形的三个顶点,这个三角形可以表例1、王爷爷家的屋顶是一个等腰例2、根据三角形的内角和是180°,三角形(如图),求顶角的度数。
你能求出下面五边形的内角和吗?40°例3、一个三角形两个内角的度数分别为35°,67°,另一个内角的度数是()°,这是一个( )三角形。
例4、在一个直角三角形中,一个锐角是75°,另一个锐角是( )。
题型三:等腰三角形和等边三角形的性质例1。
一个三角形三条边的长度分别为7厘米,8厘米,7厘米,这个三角形是( )三角形.例2.等腰三角形的底角是75°,顶角是( ),等边三角形的每个内角都是( ).例3。
一个等腰三角形的一边长5厘米,另一边长4厘米,围成这个等腰三角形至少需要()厘米长的绳子。
例4。
在一个三角形的三个角中,一个是50度,一个是80度,这个三角形既是( )三角形,又是( )三角形。
题型四、求出三角形各个角的度数。
三角形的分类考点一【三角形的分类】三角形(按角来分)锐角三角形:三个角都是锐角的三角形直角三角形:有一个角是直角的三角形钝角三角形:有一个角是钝角的三角形三角形(按边来分)三边不等三角形:三条边都不相等等腰三角形:有两条边相等等边三角形(正三角形):三条边都相按照角大小来分:三角形,三角形, 三角形。
小学三角形知识点及配
套练习题
集团文件发布号:(9816-UATWW-MWUB-WUNN-INNUL-DQQTY-
三角形
1、三角形的定义:由三条线段围成的图形(每相邻两条线段的端点相连或重合),叫三角形。
围成三角形的线段叫做三角形的边,相邻两条线段的交点叫做三角形的顶点。
2、从三角形的一个顶点到它的对边做一条垂线,顶点和垂足间的线段叫做三角形的高,这条对边叫做三角形的底。
三角形只有3条高。
重点:三角形高的画法。
3、三角形的特性:稳定性。
如:自行车的三角架,电线杆上的三角架。
4、边的关系:任意两边之和大于第三边。
三角形的周长:三边长度相加。
5、为了表达方便,用字母A、B、C分别表示三角形的三个顶点,三角形可表示成三角形ABC。
6、三角形的分类:
按照角大小来分:锐角三角形,直角三角形,钝角三角形。
按照边长短来分:等边三角形、等腰三角形、三条边都不相等的三角形
7、三个角都是锐角的三角形叫做锐角三角形。
8、有一个角是直角的三角形叫做直角三角形。
(其他两个角必定是锐角)
9、有一个角是钝角的三角形叫做钝角三角形。
(其他两个角必定是锐角)
10、每个三角形都至少有两个锐角;每个三角形都至多有1个直角;每个三角形都至多有1个钝角。
11、两条边相等的三角形叫做等腰三角形。
(等腰三角形的特点:两腰相等,两个底角相等)
12、三条边都相等的三角形叫等边三角形(正三角形) (等边三角形的三边相等,三角度数相等且每个角是60度)
13、等边三角形是特殊的等腰三角形,所有的等边三角形都是等腰三角形,等边三角形都是锐角三角形。
等腰三角形可能是锐角三角形,也可能是直角三角形,还可能是钝角三角形。
14、三角形的内角和等于180°;四边形的内角和是360°;五边形的内角和是540°
15、图形的拼组:用任意2个完全一样的三角形一定能拼成一个平行四边形。
16、用2个相同的三角形可以拼成一个平行四边形。
17、用2个相同的直角三角形可以拼成一个长方形、一个平行四边形、一个大等腰三角形。
18、用2个相同的等腰直角的三角形可以拼成一个正方形、一个平行四边形、一个大的等腰的直角的三角形。
课堂巩固练习
一、用心选一选。
1、一个三角形有()条高。
A、1
B、3
C、无数
2、如果直角三角形的一个锐角是20°,那么另一个角一定是()。
A、20°
B、70°
C、160°
3、自行车的三角架运用了三角形的()的特征。
A、稳定性
B、有三条边的特征
C、易变形
4、所有的等边三角形都是()三角形。
A、锐角
B、钝角
C、直角
5、在一个三角形中,∠1=120°∠2=36°,∠3=()
A、54°
B、24°
C、36°
二、填空.
1、三角形有()条边,()个角,()个顶点。
三角形的内角和是()。
2、等边三角形的每一个内角是()度。
3、一个等腰三角形的顶角是700,它的一个底角是()。
4、按照三角形中角的不同可以把三角形分为()三角形,()三角形和()三角形。
5、一个三角形中至少有()个锐角。
6、等腰三角形的一个底角是400,它的顶角是()度。
7、一个直角与一个锐角的和一定是一个()角。
8、在一个三角形中,∠1=42°,∠2=29°,∠3=()。
这是一个()三角形。
9、在一个三角形的三个角中,一个是50度,一个是80度,这个三角形
既是()三角形,又是()三角形。
10用长分别是5厘米、7厘米和()厘米的三根小棒一定能摆出一个三角形。
三、判断题。
(正确的画“√”,错误的画“×”)
1、等边三角形也叫正三角形。
……………………………………………()
2、等腰三角形可以是直角三角形。
………………………………………()
3、所有的等边三角形都是等腰三角形。
………………………()
4、一个顶角是80度的等腰三角形,一定是一个钝角三角形。
……
()
5、三角形任意两边的和大于第三边。
……………………………()
6、任何两个相同的三角形都能拼成一个四边形。
………………()
7、锐角三角形都有三条高。
…………………………………………
()
8、一个三角形可能有两个钝角。
………………………………()
四、按要求做一做。
1、是三角形的打“√”,不是三角形的画“○”。
()()()()
()
2、在能拼成三角形的小棒下面画“☆”。
(单位:厘米)
()()
()
3、按要求分一分。
锐角三角形有()钝角三角形有
()
直角三角形有()等腰三角形有
()
4、画出下面每个三角形底边上的高。
五、求出三角形各个角的度数。
6、下面是三块三角形玻璃打碎后留下的碎片,你能判断出它们原来各是什么三角形吗
7.解决问题
1、你能解释为什么吗
2、等腰三角形的周长是40厘米,它的一条腰长12厘米,那么,它的底边长多少厘米
3、从学校到少年宫有几种走法哪条路最近为什么
4、一个一块等腰三角形广告牌,它的一个底角是65°,它的顶角是多少度
5、王爷爷有一块菜地的形状是近似的等边三角形,一边长16cm。
如果在菜地的外面围上一圈篱笆,这个篱笆的周长大约是多少
()个三角形()个直角三角形
6、已知∠1、∠2、∠3是三角形ABC的三个内角,∠1=48°,∠
2=72°,求∠3的度数。
按角分,这是个什么三角形。