四年级下第五单元三角形知识点整理

【三角形】1、三角形的定义：由三条线段围成的图形（每相邻两条线段的端点相连或重合），叫三角形。

2、从三角形的一个顶点到它的对边做一条垂线，顶点和垂足间的线段叫做三角形的高，这条对边叫做三角形的底。

三角形只有 3 条高。

重点：三角形高的画法。

3、三角形的特性： 1、物理特性：稳定性。

如：自行车的三角架，电线杆上的三角架。

4、边的特性：任意两边之和大于第三边。

5、为了表达方便，用字母A、B、C 分别表示三角形的三个顶点，三角形可表示成三角形 ABC。

6、三角形的分类：按照角大小来分：锐角三角形，直角三角形，钝角三角形。

按照边长短来分：等边三角形、等腰三角形、三条边都不相等的三角形7、三个角都是锐角的三角形叫做锐角三角形。

8、有一个角是直角的三角形叫做直角三角形。

（其他两个角必定是锐角）9、有一个角是钝角的三角形叫做钝角三角形。

（其他两个角比定是锐角）10、每个三角形都至少有两个锐角；每个三角形都至多有 1 个直角；每个三角形都至多有 1 个钝角。

11、两条边相等的三角形叫做等腰三角形。

(等腰三角形的特点：两腰相等，两个底角相等)12、三条边都相等的三角形叫等边三角形(正三角形)(等边△的三边相等，每个角是60 度)13、等边三角形是特殊的等腰三角形14、三角形的内角和等于180°；四边形的内角和是360°；五边形的内角和是540 °15、图形的拼组：用任意 2 个完全一样的三角形一定能拼成一个平行四边形。

16、用 2 个相同的三角形可以拼成一个平行四边形。

17、用 2 个相同的直角三角形可以拼成一个长方形、一个平行四边形、一个大等腰三角形。

18、用 2 个相同的等腰直角的三角形可以拼成一个正方形、一个平行四边形、一个大的等腰的直角的三角形。

19、密铺：可以进行密铺的图形有长方形、正方形、三角形以及正六边形等。

课堂巩固练习一、用心选一选。

1、一个三角形有（）条高。

A、1B、3 C 、无数2、如果直角三角形的一个锐角是A、20° B 、 70°20°，那么另一个角一定是（C、 160°）。

人教版四年级数学下册第五单元知识点归纳整理第五单元《三角形》一、三角形的认识及特性1、三角形的定义：由3条线段围成的图形（每相邻两条线段的端点相连）叫做三角形。

2、三角形的特点：三角形有3条边、3个角和3个顶点。

3、三角形的底和高：从三角形的一个顶点到它的对边做一条垂线，顶点和垂足之间的线段叫做三角形的高，这条对边叫做三角形的底。

例如：从三角形的一个顶点到它的对边作一条垂线，如图所示：顶点顶点 边AB4、为了表达方便，用字母A、B、C分别表示三角形的三个顶点，上面的三角形可以表示成三角形ABC。

5、三角形的特性：三角形具有稳定性。

6、两点间的距离：两点间所有连线中线段最短，这条线段的长度叫做两点间的距离。

7、三角形三条边的关系：三角形任意两边的和大于第三边。

8、判断3条线段能否围城三角形，只要把较短的两条线段相加的和与最长的线段比较，大于最长的线段就能围成三角形，反之则不能。

二、三角形的分类1、三角形按角分为：锐角三角形、直角三角形和钝角三角形。

①、三个角都是锐角的三角形叫做锐角三角形；②、有一个角是直角的三角形叫做直角三角形；③、有一个角是钝角的三角形叫做钝角三角形。

用集合图形表示为：2、直角三角形的特性：3、三角形按边分为：不等边三角形和等腰三角形（等腰三角形包括等边三角形）用集合图形表示为：直角边直角边4、认识等腰三角形：在等腰三角形中，相等的两条边叫做腰，另一条边叫底；两腰的夹角叫做顶角，两腰与底边的两个夹角底温馨提示：等腰三角形可以是锐角三角形、直角三角形或钝角三角形。

在直角三角形中，如果两条直角边相等，这个直角三角形叫做等腰直角三角形，它的两个底角分别是45°.5、认识等边三角形：三条边相等的三角形叫做等边三角形（也叫正三角形）。

①、等边三角形的特点：3条边都相等，3个角都相等，每个角都是60°。

②、与等腰三角形的关系：等边三角形是特殊的等腰三角形，当等腰三角形的两条腰与底边相等时，这个等腰三角形就是等边三角形。

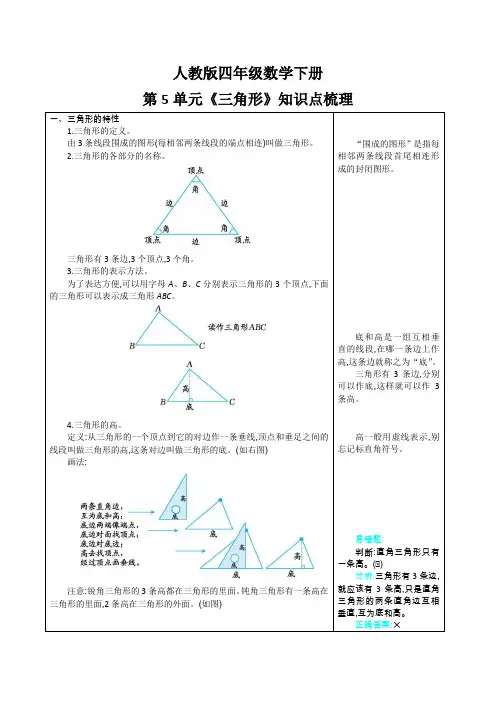
人教版四年级数学下册第5单元《三角形》知识点梳理一、三角形的特性1.三角形的定义。

由3条线段围成的图形(每相邻两条线段的端点相连)叫做三角形。

2.三角形的各部分的名称。

三角形有3条边,3个顶点,3个角。

3.三角形的表示方法。

为了表达方便,可以用字母A、B、C分别表示三角形的3个顶点,下面的三角形可以表示成三角形ABC。

4.三角形的高。

定义:从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底。

(如右图)画法:注意:锐角三角形的3条高都在三角形的里面。

钝角三角形有一条高在三角形的里面,2条高在三角形的外面。

(如图)直角三角形的两条直角边是互相垂直的,互为底和高。

(如下图所示)5.三角形的特性。

三角形具有稳定性。

6.两点间的距离。

两点间所有连线中线段最短,这条线段的长度叫做两点间的距离。

7.三角形3条边的关系。

三角形任意两边之和大于第三边。

二、三角形的分类1.用集合圈表示三角形的分类。

2.特殊三角形的特点。

等腰三角形:相等的两条边叫做三角形的腰,两腰与底边的夹角叫做底角。

等腰三角形的两腰相等,两个底角也相等。

等边三角形:等边三角形也叫做正三角形。

3条边都相等,3个角也相等,都是60°。

直角三角形:直角三角形中相互垂直的两条边叫做直角边,直角所对的边叫做斜边,斜边大于任意一条直角边。

一个三角形中最少有2个锐角。

等边三角形是特殊的等腰三角形,但等腰三角形不一定是等边三角形。

三、三角形的内角和1.三角形的内角和是180°。

2.三角形内角和的应用:在一个三角形中,已知两个角的度数,可以根据“三角形的内角和是180°”求出第三个角的度数。

典型题目:一个等腰三角形的一个内角是70°,另外两个角分别是多少度?分析:不知道70°的角是顶角还是底角,所以此题有两种可能。

解答:(180°-70°)÷2=55°或180°-70°×2=40°答:另外两个角可能都是55°,也可能一个是70°,一个是40°。

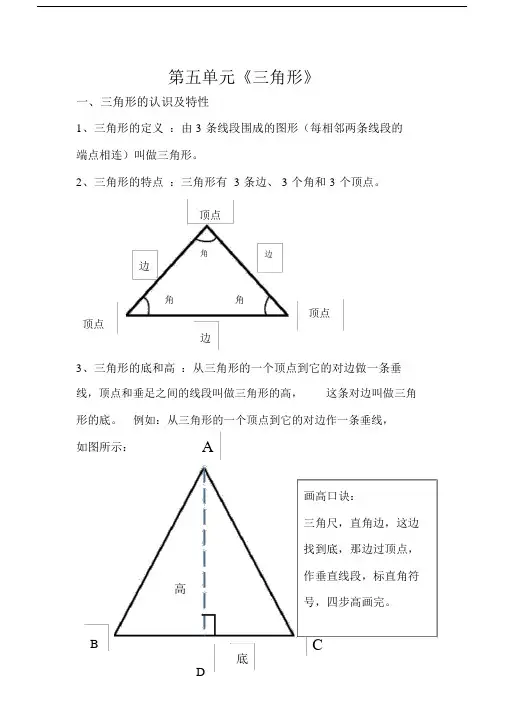
第五单元《三角形》一、三角形的认识及特性1、三角形的定义：由 3 条线段围成的图形（每相邻两条线段的端点相连）叫做三角形。

2、三角形的特点：三角形有 3 条边、 3 个角和 3 个顶点。

顶点角边边角角顶点顶点边3、三角形的底和高：从三角形的一个顶点到它的对边做一条垂线，顶点和垂足之间的线段叫做三角形的高，这条对边叫做三角形的底。

例如：从三角形的一个顶点到它的对边作一条垂线，如图所示： A画高口诀：三角尺，直角边，这边找到底，那边过顶点，作垂直线段，标直角符高号，四步高画完。

B C底D4、为了表达方便，用字母 A、B、C 分别表示三角形的三个顶点，上面的三角形可以表示成三角形ABC。

5、三角形的特性：三角形具有稳定性。

6、两点间的距离：两点间所有连线中线段最短，这条线段的长度叫做两点间的距离。

7、三角形三条边的关系：三角形任意两边的和大于第三边。

8、判断 3 条线段能否围城三角形，只要把较短的两条线段相加的和与最长的线段比较，大于最长的线段就能围成三角形，反之则不能。

二、三角形的分类1、三角形按角分为：锐角三角形、直角三角形和钝角三角形。

①、三个角都是锐角的三角形叫做锐角三角形；②、有一个角是直角的三角形叫做直角三角形；③、有一个角是钝角的三角形叫做钝角三角形。

用集合图形表示为：三角形，按角分，分清大角是窍门。

最大角，是锐角，定是锐锐角三角形角三角形。

最大角是“直”“钝”，三角形直角三角形钝角三角形类别也同名。

2、直角三角形的特性：在直角三角形中，互相垂直的两条边叫做直角直斜边边，直角所对的边叫做角边斜边，斜边大于任意一条直角边。

直角边3、三角形按边分为：不等边三角形和等腰三角形（等腰三角形包括等边三角形）① 、不等边三角②、等腰三角③、等边三角形： 3形：3 条边都不相形：有两条边相条边都相等的三角等的三角形叫做等的三角形叫形叫做等边三角形。

不等边三角形。

做等腰三角形。

（也叫正三角形）用集合图形表示为：等腰三角形不等边三角形等边三角形4、认识等腰三角形：在等腰三角形中，相等的两条边叫做腰，另一条边叫底；两腰的夹角叫做顶角，两腰与底边的两个夹角叫做底角。

四年级数学下册第五单元的必背知识点一、三角形的认识及特性1. 三角形的定义：由三条线段围成的图形 （每相邻两条线段的端点相连）叫做三角形。

2. 三角形的特点：三角形有3条边、3个角和3个顶点。

3. 三角形的底和高：从三角形的一个顶点到它的对边作一条垂线，顶点和垂足之间的线段叫做三角形的高，这条对边叫做三角形的底。

三角形只有3条高。

4. 三角形的特性：三角形具有稳定性。

如自行车的三角架、电线杆上的三角架等都是利用了三角形的稳定性。

5. 三角形三条边的关系：三角形任意两边的和大于第三边，任意两边的差小于第三边。

这是判断三条线段能否构成三角形的重要依据。

6. 三角形的分类：按角分类：锐角三角形、直角三角形和钝角三角形。

按边分类：等腰三角形 （包括等边三角形）和不等边三角形。

在等腰三角形中，相等的两条边叫做腰，另一条边叫做底；在等边三角形中，三条边都相等，三个角也都相等，每个角都是60°。

二、分数和小数的深入理解与运用1. 分数的意义和性质：分数表示的是整体的一部分。

分子表示被取走的份数，分母表示整体的份数。

分数与除法的关系：分数的分子相当于除法中的被除数，分母相当于除数。

2. 分数的运算：包括分数的加法、减法、乘法和除法。

掌握分数的基本运算规则，并能将分数化简为最简形式。

3. 小数的概念和性质：理解小数点的位置和小数位的含义。

掌握小数与分数的关系及相互转换。

4. 小数的运算：包括小数的加法、减法、乘法和除法。

掌握小数运算的规则，特别是小数点的位置处理。

5. 分数和小数的实际应用：将分数和小数应用于解决实际问题，如购物、度量转换、数据分析等。

6. 分数和小数的比较和排序：学会比较分数和小数的大小，进行排序和选择。

三、其他知识点方程的认识：初步了解方程的概念，即含有未知数的等式。

运算定律的应用：在小数和分数的运算中，运用加法交换律、结合律、乘法交换律、结合律和分配律等运算定律进行简便计算。

解决实际问题：通过应用分数、小数和三角形的知识解决实际问题，培养学生的数学应用能力和思维能力。

第五单元三角形1、三角形的定义：由三条线段围成的图形（每相邻两条线段的端点相连或重合），叫三角形。

2、从三角形的一个顶点到它的对边做一条垂线，顶点和垂足间的线段叫做三角形的高，这条对边叫做三角形的底。

三角形只有3条高。

重点：三角形高的画法。

3、三角形的特性：1、物理特性：稳定性。

如：自行车的三角架，电线杆上的三角架。

4、边的特性：任意两边之和大于第三边。

5、为了表达方便，用字母A、B、C分别表示三角形的三个顶点，三角形可表示成三角形ABC或△ABC。

6、三角形的分类：按照角大小来分：锐角三角形，直角三角形，钝角三角形。

按照边长短来分：三边不等的△，等腰△（等边三角形或正三角形是特殊的等腰△）。

等边△的三边相等，每个角是60度。

（顶角、底角、腰、底的概念）■图形与几何（三角形）（一）单元知识点具体内容第五单元：三角三角形的定义由3条线段围成的图形（每相邻两条线段的端点相连）叫做三角形。

三角形的高和底1.从三角形的一个顶点到它的对边作一条垂线，顶点和垂足之间的线段叫做三角形的高，这条对边叫做三角形的底。

2.三角形有3条高，3个底。

三角形的特性三角形具有稳定性。

三角形三边的关系三角形任意两边之和大于第三边。

（最短的两边之和大于最长边）三角形的分类1.按角分：锐角三角形、直角三角形和钝角三角形。

按边分：不等边三角形（一般三角形）、等腰三角形和等边三角形（正三角形）。

2.严格来说是两类，因为等边三角形是特殊的等腰三形角形。

三角形的内角和三角形的内角和是180°。

注：四边形内角和是360°；多边形内角和=（n-2）×180°，n≥3。

注意：1. 每个三角形最多有一个直角或钝角，最多有3个锐角，至少有2个锐角。

2.其中，既是等腰三角形又是直角三角形的，又把它叫作等腰直角三角形。

3.◎基础练习1. 下面的说法正确吗正确的画“√”，错误的画“×”。

（1）在一个三角形中，如果有两个锐角，那么这个三角形就一定是锐角三角形。

四年级数学三⾓形知识点归纳四年级数学三⾓形知识点归纳1.由3条线段围成的图形(每相邻两条线段的端点相连)叫做三⾓形。

2.三⾓形有3条边，3个⾓，3个顶点。

3.从三⾓形的⼀个顶点到它的对边做⼀条垂线，顶点和垂⾜之间的线段叫做三⾓形的⾼，这条对边叫做三⾓形的底。

4.三⾓形有3条⾼，3个底。

5.三⾓形具有稳定性，不易变形。

6.三⾓形任意两边的和⼤于第三边。

7.三⾓形任意两边的差⼩于第三边。

8.快速判断任意三条线段能否围成⼀个三⾓形：看两条较短的线段之和是否⼤于第三条线段。

9.直⾓三⾓形的两条直⾓边互为底和⾼。

10.三个⾓都是锐⾓的三⾓形，是锐⾓三⾓形。

11.有⼀个直⾓的三⾓形，是直⾓三⾓形。

12.有⼀个钝⾓的三⾓形，是钝⾓三⾓形。

13.三⾓形按⾓分：锐⾓三⾓形、直⾓三⾓形、钝⾓三⾓形13.三⾓形按边分：不等边三⾓形、等腰三⾓形、等边三⾓形14.有两条边相等的三⾓形是等腰三⾓形。

(按边)有两个⾓相等的三⾓形是等腰三⾓形。

(按⾓)15.有三条边相等的三⾓形是等边三⾓形。

(按边)有三个⾓相等的三⾓形是等边三⾓形。

(按⾓)16.等边三⾓形是特殊的等腰三⾓形。

17.等边三⾓形⼀定是锐⾓三⾓形。

18.等腰三⾓形的两腰相等，两个底⾓相等。

19.等边三⾓形的三条边相等，三个⾓也相等，都是60度。

20.等边三⾓形也叫正三⾓形。

21.等腰三⾓形中，两腰相交于⼀点形成的夹⾓是顶⾓;两腰与底相交形成的两个夹⾓是底⾓。

22.三⾓形的内⾓和是180度。

23.多边形的内⾓和=180度×(多边形的边数-2)24.任意⼀个四边形的内⾓和是360度。

25.两个完全⼀样的三⾓形可以拼成三⾓形、正⽅形、长⽅形、平⾏四边形、和四边形。

26.最少⽤2个直⾓三⾓形可以拼成⼀个长⽅形;最少⽤3个等边三⾓形可以拼成⼀个等腰梯形。

最少⽤2个等边三⾓形可以拼成⼀个菱形。

27.⽆论是什么形状的图形，没有重叠、没有空隙地铺在平⾯上，就是密铺。

28.把任何⼀个三⾓形的三个内⾓剪下来，都可以拼成⼀个平⾓。

在四年级学习三角形知识点是数学学习中的重要一步。

在这个阶段，学生们将开始学习三角形的基本概念和性质，并开始探索三角形的世界。

了解三角形的概念和性质是数学学习中的重要基础，也是学生们未来学习更加复杂的数学问题的关键。

因此，本文通过四年级三角形知识点进行总结归纳，希望对你们的学习有帮助。

1、三角形的定义：由三条线段围成的图形(每相邻两条线段的端点相连或重合)，叫三角形。

2、从三角形的一个顶点到它的对边做一条垂线，顶点和垂足间的线段叫做三角形的高，这条对边叫做三角形的底。

三角形只有3条高。

重点：三角形高的画法。

3、三角形的特性：物理特性：稳定性。

如：自行车的三角架，电线杆上的三角架。

4、边的特性：任意两边之和大于第三边。

5、为了表达方便，用字母A、B、C分别表示三角形的三个顶点，三角形可表示成三角形ABC。

6、三角形的分类：按照角大小来分：锐角三角形，直角三角形，钝角三角形。

按照边长短来分：三边不等的△，等腰△(等边三角形或正三角形是特殊的等腰△)。

等边△的三边相等，每个角是60度。

(顶角、底角、腰、底的’概念)7、三个角都是锐角的三角形叫做锐角三角形。

8、有一个角是直角的三角形叫做直角三角形。

9、有一个角是钝角的三角形叫做钝角三角形。

10、每个三角形都至少有两个锐角;每个三角形都至多有1个直角;每个三角形都至多有1个钝角。

11、两条边相等的三角形叫做等腰三角形。

12、三条边都相等的三角形叫等边三角形，也叫正三角形。

13、等边三角形是特殊的等腰三角形14、三角形的内角和等于180度。

四边形的内角和是360有关度数的计算以及格式。

15、图形的拼组：两个完全一样的三角形一定能拼成一个平行四边形。

16、用2个相同的三角形可以拼成一个平行四边形。

17、用2个相同的直角三角形可以拼成一个平行四边形、一个长方形、一个大三角形。

18、用2个相同的等腰的直角的三角形可以拼成一个平行四边形、一个正方形。

一个大的等腰的直角的三角形。