二次函数的最大值和最小值

二次函数求最值的方法一提及函数就会让很多人望而生畏，不过也有很多人热衷于探索函数的本质。

函数的概念并不难，尤其是曲线函数。

在曲线函数中，二次函数是一种重要和实际的分析方法。

这篇文章将为你普及，如何利用二次函数来求取最大值和最小值。

首先，我们必须明白函数解析式。

在数学中，函数被定义为：给定一组输入值，每个输入值都有一个对应的输出值，而这种输入和输出定义关系就称为函数。

我们有一个函数 f (x)，其中每个值 x应一个值 f (x)。

函数 f (x)阶，决定了函数的特征，其中，二次函数的解析式为：f(x)=ax2+bx+c 。

参数 a、b c为实数，并且 a≠0 。

通常情况下，求函数 f (x)最大值和最小值，只需要分析函数的解析式，就可以计算出最大值与最小值的值。

接下来，我们就来分析一下求二次函数最值的方法：二次函数最大值及最小值解法：（1）首先，求二次函数的极值点，即满足：f′(x)=0则 x= -b/2a（2）其次，求出在 x= -b/2a的函数值，即：f (-b/2a)= (a(-b/2a)2+b(-b/2a)+c）=-b2/4a+c（3）最后，比较 -b2/4a+c f (x)其它 x 上的值，若 -b2/4a+c 于其它 x 上函数值，则 x = -b/2a，函数 f (x)值-b2/4a+c 为最大值；若 -b2/4a+c于其它 x 上函数值，则其它 x 上函数值取最大值。

以上就是求解二次函数最值的方法，总结起来，我们需要做以下几件事：（1）求函数 f′(x)=0解；（2）求函数 f (-b/2a)值；（3）求最大值或最小值时，取最大或最小值。

在实际应用中，我们可以利用上述步骤求解一个二次函数的最值，该方法简单实用，也可以用来解决复杂函数的求解。

从上面可以看出，求解和研究函数可以帮助我们更好地理解数学，进而可以更好地运用它们去求解实际应用的问题。

二次函数求最值的方法正是这种应用的一种实例，不仅可以让我们更好地理解曲线函数，也可以让我们更好地应用它们来求解实际的问题。

二次函数最大最小值二次函数是一种非常常见的函数类型，其方程的一般形式为 y =ax^2 + bx + c，其中 a、b、c 是常数且a ≠ 0。

二次函数的图像通常呈现出一个开口朝上或开口朝下的抛物线形状。

在这篇文章中，我们将讨论二次函数的最大值和最小值。

一、二次函数的开口方向二次函数的开口方向由a的正负确定。

如果a>0，抛物线开口朝上；如果a<0，抛物线开口朝下。

开口方向的决定对于确定函数的最大值和最小值非常重要。

二、二次函数的顶点二次函数的最大值或最小值出现在其抛物线的顶点处。

顶点的横坐标为 x = -b / (2a)，纵坐标为 f (-b / (2a)) = a((-b / (2a))^2) +b(-b / (2a)) + c。

顶点满足的条件是一阶导数等于零，即 f' (x) =2ax + b = 0。

由此可得 x = -b / (2a)。

三、最大值和最小值的判断条件1.如果a>0，函数的最小值为顶点的纵坐标。

2.如果a<0，函数的最大值为顶点的纵坐标。

四、求解最大值和最小值的步骤1.确定二次函数的开口方向，根据a的正负判断是求最大值还是最小值。

2.计算顶点的横坐标x=-b/(2a)。

3.将顶点的横坐标代入函数表达式中计算纵坐标f(-b/(2a))。

五、实例分析现假设有一个二次函数f(x)=2x^2+5x-3，我们来求解该函数的最大值或最小值。

步骤一：确定开口方向由于a=2>0，故抛物线的开口方向朝上。

步骤二：计算顶点的横坐标将a=2、b=5代入顶点公式x=-b/(2a)，得到x=-5/(2*2)=-5/4步骤三：计算顶点的纵坐标将计算得到的顶点横坐标x=-5/4代入函数表达式f(-5/4)=2((-5/4)^2)+5(-5/4)-3，计算得到f(-5/4)=17/8所以，函数f(x)=2x^2+5x-3的最小值为17/8六、总结通过求解二次函数的最大值和最小值，我们可以知道其图像的顶点位置。

二次函数的最大小值求解方法二次函数是一种重要的数学函数形式，它可以表示为f(x)=ax2+bx+c，其中a、b和c是常数，且a eq0。

对于二次函数而言，我们通常关心它的最大值和最小值，这在数学建模和实际问题中具有重要意义。

最大值和最小值的概念在数学中，二次函数的最大值和最小值分别代表函数在某个特定区间内取得的最大和最小值。

当函数开口向上（即二次项系数a>0）时，函数的最小值在顶点处取得；当函数开口向下（即二次项系数a<0）时，函数的最大值在顶点处取得。

求解最大值和最小值的步骤步骤1：确定二次函数的标准形式首先需要将二次函数f(x)=ax2+bx+c转换为标准形式f(x)=a(x−ℎ)2+k，其中(ℎ,k)为顶点坐标。

步骤2：计算顶点坐标顶点的横坐标$h = -\\frac{b}{2a}$，通过将ℎ代入原函数得到纵坐标k。

步骤3：判断最大值和最小值根据a的正负来确定函数的开口方向，从而判断最大值或最小值。

•当a>0，函数开口向上，顶点为最小值；•当a<0，函数开口向下，顶点为最大值。

步骤4：求解最大值和最小值•最小值为数值k，即顶点坐标的纵坐标；•最大值为数值k，即顶点坐标的纵坐标。

示例假设有二次函数f(x)=2x2−8x+6，我们按照上述步骤求解：步骤1：标准形式将f(x)=2x2−8x+6转换为标准形式：f(x)=2(x−2)2+2。

步骤2：计算顶点坐标$h = \\frac{8}{4} = 2$，将ℎ=2代入原函数得到k=2，顶点坐标为(2,2)。

步骤3：判断最大值和最小值a=2>0，函数开口向上，顶点为最小值。

步骤4：求解最大值和最小值最小值为2，对应顶点(2,2)。

二次函数的最大值和最小值可以通过上述方法快速求解，在数学建模和分析问题时非常有用。

二次函数求极值公式
二次函数的一般形式是$f(x) = ax^2 + bx + c$，其中$a$、$b$、$c$ 是常数，且$a \neq 0$。

要求二次函数的极值（最大值或最小值），可以使用以下公式：
1. 首先，计算二次函数的判别式$\Delta = b^2 - 4ac$。

2. 如果$\Delta > 0$，则二次函数有两个不相等的实根，此时极值点为抛物线的顶点，顶点的横坐标为$x = -\frac{b}{2a}$。

-如果$a > 0$，则顶点为最小值点，最小值为$f(-\frac{b}{2a})$。

-如果$a < 0$，则顶点为最大值点，最大值为$f(-\frac{b}{2a})$。

3. 如果$\Delta = 0$，则二次函数有唯一实根，此时极值点为抛物线的顶点，顶点的横坐标为$x = -\frac{b}{2a}$。

-如果$a > 0$，则顶点为最小值点，最小值为$f(-\frac{b}{2a})$。

-如果$a < 0$，则顶点为最大值点，最大值为$f(-\frac{b}{2a})$。

4. 如果$\Delta < 0$，则二次函数没有实根，此时函数在定义域内没有极值点。

这些公式可以帮助你找到二次函数的极值点和极值。

二次函数的最大值与最小值y 0ax2bx c aa x b2a 24a c4 ab2一、判断的基本方法a 当当a 0时，二次函数有最小值0时，二次函数有最大值二、求最值的类型与方法㈠在顶点处直接取得例：求y x22x 3最大值或最小值2y x1 4解：x R当x1时，y的最大值为4.㈡不能在顶点处取得例：求下列函数的最大值或最小值：1. 3231y x2x x解：y239 xx 22 4 2321743 3,1 23 17 当x y -2 4 时， 的最小值为 当x1时，y 的最大值为212y xxx2.21, 3,15解：y12x 5 65 53,1根据图像看，在-31y x区间上随的增大而减小当x3时，y的最大值为26 5当x1时，y的最小值为-6 512y x x x3. 21,1,22解：y 12x2 3 21,22根据图像看，y随x的增大而增大当x1时，y的最小值为-5 2当x2时，y的最小值为5㈢带有参数的二次函数求最值1 5例1：当t x t1时，求函数y x2x的最小值（其中t为实数）22125解：函数y x x x1，见下图的对称轴为2 2①当对称轴在所给范围的左侧时，即t>1时，当x t时，y的最小值为1t2t2 5 2②当对称轴在所给范围的之间时，即t 1t 10t1时，当x1时，y的最小值为1251-1-2 2-3③当对称轴在所给范围的右侧时，即t 1＜1t＜0时，当x t1时，y的最小值为1t 2t 51t 231 122 2例2.求函数y 2x2ax1，当0x1时的最小值。

解：函数y 2x2ax1，对称轴为a x2 2a4a a 0x1y x xy ①当0，即0 时，在范围内，随的增大而增大，当=0 时，最4小，y 的最小值= 202a 01 1a a②当0＜＜1，即0＜a＜4时，当x时，有最小值，4 4y的最小值= 22a a a2a1 1 448a③当1，即时，在范围内，随的增大而减小，当=1时，最a40x1y x x y 4小，y的最小值=212a113a7、我们各种习气中再没有一种象克服骄傲那麽难的了。

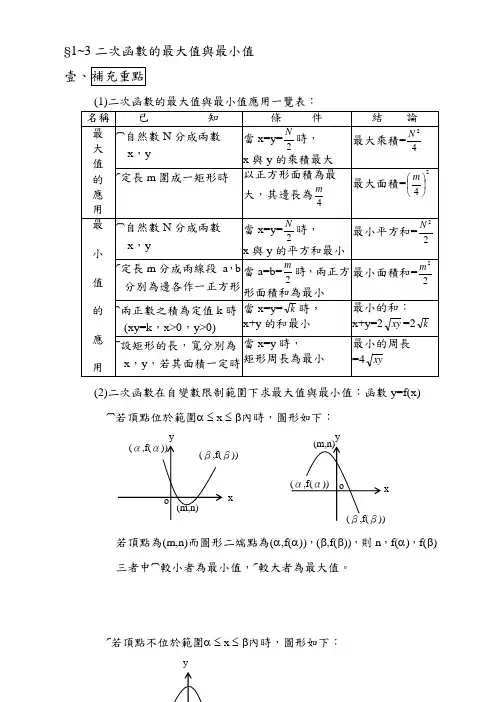
§1~3二次函數的最大值與最小值(1)二次函數的最大值與最小值應用一覽表：(2)二次函數在自變數限制範圍下求最大值與最小值：函數y=f(x) 若頂點位於範圍α ≤ x ≤ β內時，圖形如下：若頂點為(m,n)而圖形二端點為(α,f(α))，(β,f(β))，則n ，f(α)，f(β)三者中 較小者為最小值， 較大者為最大值。

若頂點不位於範圍α ≤ x ≤ β內時，圖形如下：xy)) xy y圖形二端點為(α,f(α))，(β,f(β))，則f(α)，f(β)二者中 較小者為最小值， 較大者為最大值。

(3)最大值與最小值的求法，除可利用二次函數來求外，尚可利用下列的方法： 利用ab ba ≥+2(算術平均數)≥(幾何平均數) 例：二正數x ，y ，若xy=24，求2x+3y 之最小值。

∵()()y x yx 32232≥+ 2x+3y xy 62≥∴ 2x+3y ≥2144=24 故最小值為24 利用∣a ∣+∣b ∣≥∣a+b ∣例：設x 為實數，求∣x+2∣+∣x -5∣之最小值。

∵∣x+2∣+∣x -5∣=∣x+2∣+∣5-x ∣≥∣(x+2)+(5-x)∣ =7∴∣x+2∣+∣x -5∣≥7 故最小值為7 利用一元二次方程式D ≥0例：設k 為實數，方程式x 2-(k -1)x+(k 2-1)=0有實根，求k 之最大值與最小值。

∵方程式有實根 ∴D ≥0⇒[-(k -1)]2-4×1×(k 2-1)≥0 (k -1)(k -1-4k -4)≥0⇒ (k -1)(3k+5)≤0∴ 1≥k ≥-35，故 k 之最大值為1，最小值為-35。

分式型：當分子為定值，分母最大時分式的值為最小；分母最小x(β,f(β))時分式的值為最大。

例：設x 為實數，求y=4x 2x 122++ 之最大值。

∵ x 2+2x+4=(x 2+2x+1)+3=(x+1)2+3≥3∴當x=-1時，x 2+2x+4有最小值3，此時y 有最大值312=4。

初二数学重要知识点整理：二次函数的最大值和最小值、概率的意义初二数学重要知识点整理：二次函数的最大值和最小值、概率的意义二次函数的最值：1.如果自变量的取值范围是全体实数，则当a0时，抛物线开口向上，有最低点，那么函数在处取得最小值y最小值=；当a0时，抛物线开口向下，有最高点，即当时，函数取得最大值，y最大值=。

也即是：如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当时，。

2.如果自变量的取值范围是，那么，首先要看是否在自变量取值范围内，若在此范围内，则当x=时，；若不在此范围内，则需要考虑函数在范围内的增减性，如果在此范围内，y随x的增大而增大，则当x=x2 时，，当x=x1 时；如果在此范围内，y随x的增大而减小，则当x=x1时，，当x=x2时概率的基本性质（互斥事件、对立事件）互斥事件：事件A和事件B不可能同时发生，这种不可能同时发生的两个事件叫做互斥事件。

如果A1，A2，…，An中任何两个都不可能同时发生，那么就说事件A1，A2，…An彼此互斥。

对立事件：两个事件中必有一个发生的互斥事件叫做对立事件。

注：两个对立事件必是互斥事件，但两个互斥事件不一定是对立事件。

事件A+B的意义及其计算公式：（1）事件A+B：如果事件A，B中有一个发生发生。

（2）如果事件A，B互斥时，P（A+B）=P（A）+P（B），如果事件A1，A2，…An彼此互斥时，那么P（A1+A2+…+An）=P（A1）+P（A2）+…+P（An）。

概率的几个基本性质：（1）概率的取值范围：[0，1].（2）必然事件的概率为1.（3）不可能事件的概率为0.（4）互斥事件的概率的加法公式：如果事件A，B互斥时，P（A+B）=P（A）+P（B），如果事件A1，A2，…An彼此互斥时，那么P（A1+A2+…+An）=P（A1）+P（A2）+…+P（An）。

如果事件A，B对立事件，则P（A+B）=P（A）+P（B）=1。

二次函数顶点式最大值最小值求法
二次函数是高中数学中一个重要且常见的函数，表示为y=ax2+bx+c。

其中，a、b、c分别是二次、一次和常数项系数，a不等于零。

二次函数的图像是一个抛物线，其开口方向取决于a的正负性。

顶点式表示二次函数
二次函数的标准形式是y=ax2+bx+c，一般形式是y=ax2+bx+c。

而二次函数的顶点式则表示为y=a(x−ℎ)2+k，其中(ℎ,k)为抛物线的顶点坐标。

顶点式更方便计算顶点坐标以及最大值和最小值。

求二次函数的最值
最小值
对于二次函数y=a(x−ℎ)2+k，当a>0时，二次函数的最小值为k，此时抛物线开口向上，顶点为最小值点。

最大值
当a<0时，二次函数的最大值为k，此时抛物线开口向下，顶点为最大值点。

求解例题
现考虑二次函数y=2(x−3)2+1，求最大值和最小值。

根据顶点式的特性，可直接得出该函数最小值为1，最大值不存在。

总结
通过二次函数的顶点式表示，可以简便地求得二次函数的最小值和最大值。

当二次函数为y=a(x−ℎ)2+k，其中a的正负性决定了函数的凹凸性，从而确定了最小值或最大值的存在性及数值大小。

最值的求法比较直观，可通过直接观察抛物线的开口和顶点位置进行判断。

二次函数的最大值与最小值许多人都知道当把一个苹果抛向空中时，苹果会飞向空中，但它的速度会逐渐减小，并最终不向上运动（瞬间静止在空中），之后再加速落下。

这是因为物体受重力的缘故。

但其实，将苹果运行的时间与高度在坐标系中画出来，就是一个弧线，而且不是一般的弧线，是二次函数。

对于一个二次函数来说，它有正向的弧，也有倒的弧。

正弧的最高点是函数的最大值，而倒向的最低点则是最小值。

今天，我们就围绕着二次函数的最大与最小值来到论一下。

摘要：通过对二次函数的一些研究，来了解并掌握求二次函数的最大与最小值的方法。

一、出现的原因二次函数之所以会出现最大至于最小值，我们就要从它的根源说起。

二次函数的表达式可写为y=ax2+bx+c（abc均为常数，a≠0），其中的ax2+bx+c与我们所学一元二次方程有几分相像。

其实，二次函数与一元二次方程的就如同一次函数与二元一次方程的关系基本一致。

我们可以把原式写为ax2+bx+c+y=0，为了方便讨论且自变量与因变量的影响是互相的，所以我们就先假设y是改变x的自变量。

那么每一次在求值时我们都会先取一个y的值。

这时，y就可以看做一个常数那么我们就把它与常数项c写在一起，即ax2+bx+（c+y）=0，这下子整个式子中只有x是一个变量，这个式子也就是一个地地道道的一员二次方程了。

而这个方程中abc 是固定不变的，因而y的改变会改变式子的常数项，这样一来，在解方程的时候, (c+y)的值与前面的ab相配合组成的方程可能有两个不相等的实根或两个相等的实根或没有实根。

这也就说明了当y值固定时，可能有两个x满足，或只有一个，或没有。

再从x的角度来说，有两个x可以造成同一个y值，但这两个点关于一个点对称，这个点就是特殊点，即最大（小）值，而不论x如何变化，y总有一道不可逾越的鸿沟，到达固定点后就会折返。

因此二次函数的这一特性造就了它的最大（小）值。

二、判定最大还是最小既然二次函数有最大或最小值，那么那种会有最大值，那种会有最小值呢？我们就来讨论一下。

初中数学二次函数的图像的最小值和最大值有什么关系
二次函数的图像的最小值和最大值之间有着密切的关系。

以下是对二次函数图像的最小值和最大值之间关系的详细解释：
1. 开口向上的二次函数图像：对于开口向上的二次函数图像，顶点是图像的最小值。

也就是说，在顶点处，二次函数图像达到了最低点。

顶点的纵坐标值就是二次函数图像的最小值。

与最小值相对应的横坐标值是顶点的横坐标。

2. 开口向下的二次函数图像：对于开口向下的二次函数图像，顶点是图像的最大值。

也就是说，在顶点处，二次函数图像达到了最高点。

顶点的纵坐标值就是二次函数图像的最大值。

与最大值相对应的横坐标值是顶点的横坐标。

因此，二次函数图像的最小值和最大值是由顶点的纵坐标值决定的。

开口向上的二次函数图像的最小值是顶点的纵坐标值，开口向下的二次函数图像的最大值是顶点的纵坐标值。

此外，我们还可以通过顶点的横坐标值来确定最小值和最大值所对应的自变量的取值。

也就是说，在顶点处，最小值和最大值所对应的x 值是相同的。

综上所述，二次函数图像的最小值和最大值是由顶点的纵坐标值决定的，而顶点的横坐标值表示最小值和最大值所对应的自变量的取值。

理解和利用顶点的位置和开口方向，有助于我们分析和解释二次函数图像的特征和行为。

需要注意的是，二次函数图像可能不存在最小值或最大值，这取决于二次函数的系数和定义域的限制。

当二次函数的系数 a 大于0 且定义域为全体实数时，图像是开口向上的，没有最大值；当二次函数的系数 a 小于0 且定义域为全体实数时，图像是开口向下的，没有最小值。

二次函数区间最值问题二次函数在数学中是非常重要的一种函数类型。

它具有许多特殊的性质，例如顶点，对称轴和开口方向等。

在求解二次函数最值问题时，我们需要注意一些特殊情况，并运用二次函数的性质进行判断和求解。

一、二次函数的基本形式二次函数是指含有二次项的一元二次方程。

一般表示为y=ax^2+bx+c（a≠0）。

其中，a代表开口方向和轴对称的大小，正数表示开口向上，负数表示开口向下；b代表对称轴与y轴的交点，c代表二次函数与y轴的交点。

二、求解二次函数的最大值和最小值对于给定二次函数y=ax^2+bx+c（a≠0），我们需要求出它的最大值和最小值。

为了求解这个问题，我们需要掌握以下两种方法：方法一：利用二次函数的对称性求解二次函数的对称轴公式为x=-b/2a，对称轴将二次函数分成两个对称部分。

在对称轴的左侧和右侧二次函数的值是相等的。

因此我们只需要计算对称轴左侧（或右侧）的值即可。

当二次函数开口向上时，它的最小值就在对称轴上。

当二次函数开口向下时，它的最大值就在对称轴上。

因此我们可以根据开口方向来判断出最大值和最小值的位置。

同时我们还可以使用完全平方公式来求出二次函数的最大值和最小值：对于开口向上的二次函数y=ax^2+bx+c，最小值为：y=[4ac-b^2]/4a对于开口向下的二次函数y=ax^2+bx+c，最大值为：y=[4ac-b^2]/4a这个公式可以提高计算的速度，同时也可以通过它的形式来理解二次函数的最大值和最小值。

方法二：利用导数求解导数是求解最值问题中非常实用的工具。

对于二次函数y=ax^2+bx+c，它的导数为y'=2ax+b。

因此当y'=0时，二次函数y取得极值，将y'=0代入原函数，我们可以得到极值为：y=-b^2/4a+c因为这个式子中，b^2/4a代表着对称轴的位置，因此这个公式也是方法一的变形。

在这个公式中，我们直接可以求出函数的最大值或最小值。

三、计算例题实例一：求解二次函数y=2x^2+4x+1的最小值和最大值。

二次函数的最值与单调性二次函数是指拥有形如y = ax^2 + bx + c的函数，其中a、b、c是实数且a ≠ 0。

本文将讨论二次函数的最值和单调性。

一、最值二次函数的最值可以通过其抛物线的开口方向来确定。

如果a > 0，抛物线开口向上，该二次函数的最小值就是它的顶点；如果a < 0，抛物线开口向下，该二次函数的最大值同样是它的顶点。

1. 最小值当二次函数的开口向上且a > 0时，我们可以通过求解顶点的坐标来得到最小值。

顶点的x坐标可以通过公式x = -b / (2a)计算得出，而对应的y值即为最小值。

举个例子，考虑函数y = x^2 + 2x + 1，通过计算可得到顶点坐标(-1, 0)，因此最小值为0。

2. 最大值当二次函数的开口向下且a < 0时，同样可以通过顶点的坐标来计算最大值。

顶点的求解方式与上述相同，只是它对应的y值即为最大值。

举个例子，考虑函数y = -x^2 + 2x - 1，通过计算可得到顶点坐标(1,0)，故最大值为0。

二、单调性二次函数的单调性取决于a的正负性。

当a > 0时，二次函数为增函数；当a < 0时，二次函数为减函数。

1. 增函数当二次函数的a > 0时，表示抛物线开口向上，函数呈现出向上的凸性。

这意味着随着自变量的增大，函数值也随之增大。

举个例子，考虑函数y = x^2，可以看到，随着x的增加，y的值逐渐增大。

2. 减函数当二次函数的a < 0时，表示抛物线开口向下，函数呈现出向下的凹性。

这表明随着自变量的增大，函数值会减小。

举个例子，考虑函数y = -x^2，可以观察到，随着x的增加，y的值逐渐减小。

总结：二次函数的最值和单调性可以通过抛物线的开口方向、顶点以及a 的正负性来确定。

对于最值，当抛物线开口向上时，二次函数的最小值为顶点的纵坐标；当抛物线开口向下时，二次函数的最大值同样为顶点的纵坐标。

对于单调性，当a > 0时，二次函数为增函数；当a < 0时，二次函数为减函数。