24-伽利略变换例题

伽利略变换公式推导摘要：1.引言2.伽利略变换的定义和意义3.坐标系的选取和变换4.伽利略变换的公式推导5.实例分析6.结论正文：【引言】在经典力学中，伽利略变换是一种非常重要的数学工具，它描述了在不同惯性参考系中物理规律的相对性。

本文将详细介绍伽利略变换的定义、公式推导及实例分析。

【坐标系的选取和变换】在讨论伽利略变换之前，我们先了解一下坐标系的概念。

坐标系是用来描述物体运动状态的工具，选取合适的坐标系可以简化问题。

设有两个惯性坐标系S和S"，其中S为原始坐标系，S"为变换后的坐标系。

【伽利略变换的定义和意义】伽利略变换是基于相对性原理推导出来的，它表示在两个惯性坐标系中物理规律的相互关系。

伽利略变换的意义在于揭示了物理规律的相对性，即物理规律在任何惯性坐标系中都是相同的。

【伽利略变换的公式推导】设有一物体在坐标系S中的坐标为（x，y，z），在坐标系S"中的坐标为（x"，y"，z"）。

根据伽利略变换的定义，我们有以下关系：x" = γ(x - vt)y" = γ(y - vt)z" = γ(z - vt)其中，γ表示洛伦兹因子，v为S和S"之间的相对速度。

【实例分析】以电磁波为例，设电磁波在坐标系S中的频率为f，传播速度为c。

在坐标系S"中，电磁波的频率为f"，传播速度为c"。

根据伽利略变换，我们有：f" = f / γc" = c * γ【结论】伽利略变换是描述惯性坐标系中物理规律相对性的重要工具，通过选取合适的坐标系，可以简化问题的求解。

通过本文的介绍，希望大家能够更好地理解伽利略变换的定义、公式及应用。

伽利略变换求物体相对速度伽利略变换是描述物体相对运动的一种方法，它可以用于求解物体的相对速度。

本文将通过具体的示例来说明伽利略变换的原理及其在求解物体相对速度中的应用。

伽利略变换是由意大利物理学家伽利略提出的，它基于相对运动的概念，认为在相对静止的参考系中，物体的运动状态是相对的，即不受到参考系的影响。

根据这一观点，我们可以使用伽利略变换来描述物体的相对运动。

假设有两个物体A和B，分别以速度vv和速度vv在同一个直线上运动。

我们希望求解物体A相对于物体B的速度，即vv'。

首先，我们需要建立一个相对静止的参考系v，它是一个观察者静止不动的参考系。

在参考系v中，物体A的速度为vv，物体B的速度为vv。

假设物体A和物体B在v=0的时候位于原点，我们可以得到物体A和物体B在参考系v中的位置随时间的变化关系为：vv = vvvvv = vvv现在，让我们切换到以物体B为参考系的观察者，即参考系v'。

在v'中，物体B静止不动，物体A的速度变为vv'，我们希望求解物体A相对于物体B的速度。

根据伽利略变换的原理，我们可以得到物体A在v'中的位置随时间的变化关系为：vv' = vv - vv= vvv - vvv= (vv - vv)v根据上述式子，我们可以看出物体A相对于物体B的速度为(vv - vv)。

这个结果表明，物体的相对速度是由它们各自的速度相减得到的。

当两个物体的速度方向相同时，它们的相对速度为两个速度的差值。

当两个物体的速度方向相反时，它们的相对速度为两个速度的和值。

例如，假设有两辆汽车A和B，汽车A以40米/秒的速度向东行驶，汽车B以30米/秒的速度向西行驶。

我们想要求解汽车A相对于汽车B的速度。

根据伽利略变换的原理，我们可以得到汽车A相对于汽车B的速度为(40 - (-30)) = 70米/秒。

这个结果告诉我们，从汽车B的参考系观察，汽车A以每秒70米的速度向西行驶。

伽利略变换公式推导摘要：1.伽利略变换的概念2.伽利略变换的公式推导3.伽利略变换的应用正文：一、伽利略变换的概念伽利略变换，是物理学中一种描述不同惯性参考系下物体运动规律的坐标变换。

在经典力学中，伽利略变换主要用于研究在惯性参考系中运动的物体，在非惯性参考系中的运动规律。

这种变换方式由意大利物理学家伽利略提出，被广泛应用于经典力学和相对论的研究中。

二、伽利略变换的公式推导伽利略变换的公式推导过程如下：假设有一个物体在惯性参考系S 中运动，其速度为v，经过时间t 后，物体的位移为x。

现在我们考虑在非惯性参考系S"中观察该物体的运动。

在惯性参考系S 中，物体的位移可以表示为：x = vt。

在非惯性参考系S"中，由于存在加速度a，物体的位移需要考虑加速度的影响。

假设物体在S"系中的初速度为v"，经过时间t"后，物体的位移为x"。

根据物理学的速度叠加原理，我们可以得到：x" = v"t" + 1/2 * a * t"^2.由于在非惯性参考系S"中，物体的初速度v"和加速度a 与惯性参考系S中的速度v 和时间t 之间存在关系。

根据伽利略变换的定义，我们可以得到：v" = v - a * t，a = a" - v^2 / r，其中，a"表示非惯性参考系S"中的加速度，r 表示物体在S 系中的半径。

将上述关系代入x"的公式中，我们可以得到伽利略变换的公式：x" = v(t - t") - 1/2 * (a" - v^2 / r) * (t - t")^2。

这就是伽利略变换的公式推导过程。

三、伽利略变换的应用伽利略变换在物理学中有广泛的应用，例如：1.研究在非惯性参考系中的物体运动，如地球表面附近自由落体的运动规律；2.在相对论中，伽利略变换是描述不同惯性参考系下物体运动规律的基础，是构建洛伦兹变换和闵可夫斯基变换的基础；3.在卫星导航系统中，由于卫星的运动速度非常快，需要考虑非惯性参考系下的物体运动规律，因此伽利略变换在卫星导航系统中有重要的应用。

伽利略变换公式范文
设想有两个相对静止的参考系S和S'，其中S'以速度v相对于S运动，两个参考系的坐标原点重合。

1.从S到S'的伽利略变换公式：
设一个在S系中以速度u运动的物体，在S'系中的速度为u'，则有如下关系：
u'=u-v
其中，u'表示物体在S'系中的速度，u表示物体在S系中的速度，v 表示S'系相对于S系的速度。

2.从S'到S的伽利略变换公式：
设一个在S'系中以速度u'运动的物体，在S系中的速度为u，则有如下关系：
u=u'+v
其中，u表示物体在S系中的速度，u'表示物体在S'系中的速度，v 表示S'系相对于S系的速度。

伽利略变换公式是经典力学中描述参考系之间运动变换的重要工具。

它在解决具有区分静止参考系和运动参考系的力学问题时，提供了便利和简化。

但是在高速运动和极端条件下，相对论效应会对运动的描述产生影响，此时就需要使用相对论中的洛伦兹变换。

总结起来，伽利略变换公式是描述在牛顿力学下，相对参考系之间运动变换的公式。

它适用于低速运动的物体，对于高速运动的物体需要考虑
相对论效应。

伽利略变换公式提供了简便的方法来描述参考系之间的运动关系。

§2、2 伽利略变换2、2、1 伽利略变换（1） 如图2-2-1所示，有两个惯性 系S 和'S ， 它们对应的坐标轴相互平行，且当t ='t =0时，两系的坐标原点'O 与O 重合。

设'S 系相对于S 系沿x 轴正方向以速度u 运动。

同一质点P 在某一时刻在S 系中的时空坐标为(x,y,z,t)，在S`系中的时空坐标为 （x’,y’,z’,t’）⎪⎪⎩⎪⎪⎨⎧===-=t t zz y y ut x x '''' 即t u r r -='或 (1) x=x '＋ｕｔ ⎪⎩⎪⎨⎧==='''t t z z y y 即 t u r r+='式（1）称为伽利略时空坐标变换公式。

（２）将式（1）中的空间坐标分别对时间求一次导数得：图2-2-1⎪⎪⎪⎩⎪⎪⎪⎨⎧====-=-==z z y y x x v dt dz v v dt dy v u v u dt dxdt dx v '''''' 即u v v -= ' 或⎪⎪⎪⎩⎪⎪⎪⎨⎧======+=+==z z y yx x v dt dz dt dz v v dt dy dt dy v u v u dt dx dt dx v '''''1即u v v '+'= （2）式（2）称为伽利略速度变换公式。

（3）将式（2）再对时间求一次导数得⎪⎪⎪⎩⎪⎪⎪⎨⎧=='='=='='=='='z z z z y y y y x x xxa dt dv dt v d a a dt dv dt v d a a dt dv dt v d a 即a a ='⎪⎩⎪⎨⎧'='='=z z y y x x a a a a a a a a'= （3） 式（3）表明在伽利略变换下加速度保持不变。

伽利略变换是物理学中描述相对运动的经典理论，它描述了两个参考系之间的一种特殊关系。

伽利略变换的数学表达式取决于坐标系的选择，通常涉及速度、加速度和位置等物理量。

假设有两个参考系A和B，它们相对于彼此运动。

在A参考系中观测到物体在B参考系中的位置、速度和加速度，我们可以使用伽利略变换来表达这些物理量之间的关系。

在数学上，伽利略变换可以用线性方程组表示，其中包含了物体的位置、速度和加速度。

以下是一个简化的伽利略变换的数学表达式：
XA(t) = XB(t-Δt) + VBA(t) * Δt
YA(t) = YB(t-Δt) + ABA(t) * Δt^2 / 2
其中：
* XA和YA是A参考系中物体在时间t的位置；
* XB和YB是B参考系中物体在时间t-Δt的位置；
* VBA和ABA是物体在从B到A的相对运动中的速度和加速度；
* Δt是时间间隔。

这个表达式描述了物体在两个参考系之间的相对运动，其中Δt通常可以视为非常短的时间间隔，因为相对运动通常是在短时间内发生的。

值得注意的是，伽利略变换只适用于惯性参考系之间的相对运动。

这意味着物体在做匀速直线运动或不受外力作用时，它们的运动可以被视为惯性运动，符合伽利略变换的条件。

在非惯性参考系中（例如，受到重力作用的自由落体或弹跳球），需要使用其他更复杂的理论来描述物体的运动，例如洛伦兹变换。

以上是对伽利略变换的简要介绍，如果你需要更具体或更详细的讨论，建议查阅相关物理学教材或论文。

伽利略变换证明牛顿第二定律
伽利略变换描述了物体在惯性参考系中的运动状态如何转换到另一个惯性参考系中。

这个变换过程不会改变物体的运动状态，包括速度和加速度等。

因此，可以使用伽利略变换来证明牛顿第二定律。

牛顿第二定律说，物体的加速度与物体的力成正比，与物体的质量成反比。

即：
F = ma
其中，F是施加在物体上的力，m是物体的质量，a是物体的加速度。

现在假设一个物体在惯性参考系A中受到一个力F，它的加速度为a。

根据伽利略变换，可以得到在另一个惯性参考系B中，物体的速度和加速度分别为：
v' = v - u
a' = a
其中，v是物体在A参考系中的速度，u是A参考系相对于B参考系的相对速度，v'和a'是物体在B参考系中的速度和加速度。

假设在B参考系中，物体的质量是m'，它所受到的力是F'。

根据牛顿第二定律，在B参考系中物体的加速度为：
a' = F'/m'
将伽利略变换中的a'代入上式，得到：
a = a'
将牛顿第二定律中的F和m代入上式，得到：
F/m = F'/m'
因此，可以得到：
F' = F
这意味着，无论在哪个惯性参考系中，物体受到的力都是相同的。

这就是牛顿第二定律的一个关键结论。

所以，我们可以使用伽利略变换来证明牛顿第二定律，在不同的惯性参考系中力和加速度的关系是相同的。

伽利略速度变换的原理伽利略速度变换是指在经典物理学中，伽利略变换下的速度变换规律。

伽利略速度变换的原理主要包括相对性原理和相加规则。

一、相对性原理相对性原理是伽利略速度变换的基础，它认为物理规律在不同的惯性参考系中都是一样的。

也就是说，无论是在静止的参考系还是在匀速直线运动的参考系中，物理规律都不会发生变化。

二、相加规则在伽利略速度变换中，相加规则指出两个物体的速度在相对性原理下如何相加。

假设有两个参考系S和S'，其中S'相对于S以速度v做匀速直线运动。

设物体A相对于S的速度为u，相对于S'的速度为u'，则有如下关系：u' = u - v这个关系表明，在伽利略变换下，如果两个参考系相对于某个参考系的速度相差v，则物体在两个参考系中的速度相差v。

三、实例分析为了更好地理解伽利略速度变换的原理，我们来看一个例子。

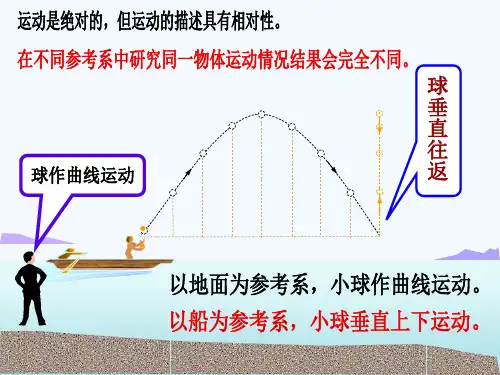
假设有一个小船以速度v相对于岸边做匀速直线运动，而一个人以速度u相对于小船做匀速直线运动。

我们需要求出这个人相对于岸边的速度。

根据相对性原理，我们可以选择小船为参考系S，人为参考系S'。

在小船的参考系中，小船静止，人以速度u相对于小船运动。

而在岸边的参考系中，小船以速度v运动，人以速度u'相对于岸边运动。

根据相加规则，我们有：u' = u - v根据这个式子，我们可以得出人相对于岸边的速度。

通过这个例子，我们可以看出伽利略速度变换的原理在经典物理学中的应用。

无论是在相对静止的参考系还是在相对运动的参考系中，物体的速度变换都遵循相对性原理和相加规则。

需要注意的是，伽利略速度变换只适用于低速运动，当物体的速度接近光速时，就需要使用相对论速度变换来计算。

相对论速度变换与伽利略速度变换有所不同，它遵循狭义相对论的原理，包括洛伦兹变换等。

总结起来，伽利略速度变换是经典物理学中速度变换的基本原理之一。

它通过相对性原理和相加规则，描述了物体在不同参考系中的速度关系。

伽利略变换的逆变换
（实用版）
目录
1.伽利略变换的概念
2.伽利略变换的逆变换
3.伽利略变换和逆变换的关系
4.应用实例
正文
一、伽利略变换的概念
伽利略变换是一种在经典力学中描述物体运动规律的数学变换。

它是意大利科学家伽利略·伽利莱在研究自由落体运动时发现的。

伽利略变换可以将一个惯性系中的观测结果转换到另一个惯性系中，从而解释在不同惯性系下物体运动的规律。

二、伽利略变换的逆变换
伽利略变换的逆变换是指在已知两个惯性系之间的相对运动状态，以及其中一个惯性系中的观测结果，求另一个惯性系中的观测结果。

逆变换与伽利略变换的原理相同，只是变换的方向相反。

三、伽利略变换和逆变换的关系
伽利略变换和逆变换是相互关联的，它们共同构成了一个完整的数学体系。

在实际应用中，我们可以通过伽利略变换将一个惯性系中的物理规律转换到另一个惯性系中，然后通过逆变换求解该惯性系中的物理现象。

四、应用实例
伽利略变换和逆变换在物理学、天文学等领域有广泛的应用。

例如，在研究地球自转和公转时，我们可以通过伽利略变换将地球上的观测结果
转换到太阳系参考系中，然后通过逆变换求解地球在太阳系参考系中的运动规律。