雷诺实验带数据处理
- 格式:doc
- 大小:256.00 KB
- 文档页数:8

一、实验目的1. 观察层流和紊流的流态及其转换特征。
2. 通过临界雷诺数,掌握圆管流态判别准则3. 掌握误差分析在实验数据处理中的应用。
二、实验原理1、实际流体的流动会呈现出两种不同的型态:层流和紊流,它们的区别在 于:流动过程中流体层之间是否发生混掺现象。
在紊流流动中存在随机变化的脉 动量,而在层流流动中则没有,如图 1所示。
2、圆管中恒定流动的流态转化取决于雷诺数。
雷诺根据大量实验资料,将 影响流体流动状态的因素归纳成一个无因次数,称为雷诺数 Re ,作为判别流体流动状态的准则式中 Q ――流体断面平均流量,L sD ----- 圆管直径,mm――流体的运动粘度,m 2;s在本实验中,流体是水。
水的运动粘度与温度的关系可用泊肃叶和斯托克斯 提出的经验公式计算36((0.585 10 (T 12) 0.03361) (T 12) 1.2350) 10式中 ——水在t C 时的运动粘度,m 2:s ;T ――水的温度,C 。
3、判别流体流动状态的关键因素是临界速度。
临界速度随流体的粘度、密 度以及流道的尺寸不同而改变。
流体从层流到紊流的过渡时的速度称为上临界流 速,从紊流到层流的过渡时的速度为下临界流速。
4、圆管中定常流动的流态发生转化时对应的雷诺数称为临界雷诺数,对应 于上、下雷诺实验Re4QD临界速度的雷诺数,称为上临界雷诺数和下临界雷诺数。
上临界雷诺数表示超过此雷诺数的流动必为紊流,它很不确定,跨越一个较大的取值范围。
而且极不稳定,只要稍有干扰,流态即发生变化。
上临界雷诺数常随实验环境、流动的起始状态不同有所不同。
因此,上临界雷诺数在工程技术中没有实用意义。
有实际意义的是下临界雷诺数,它表示低于此雷诺数的流动必为层流,有确定的取值。
通常均以它作为判别流动状态的准则,即Re < 2320 时,层流Re > 2320 时,紊流该值是圆形光滑管或近于光滑管的数值,工程实际中一般取Re = 2000。

试验七雷诺试验一、试验目旳1.观测液体流动时旳层流和紊流现象。
辨别两种不一样流态旳特性, 弄清两种流态产生旳条件。
分析圆管流态转化旳规律, 加深对雷诺数旳理解。
2、测定颜色水在管中旳不一样状态下旳雷诺数及沿程水头损失。
绘制沿程水头损失和断面平均流速旳关系曲线, 验证不一样流态下沿程水头损失旳规律是不一样旳。
深入掌握层流、紊流两种流态旳运动学特性与动力学特性。
3、通过对颜色水在管中旳不一样状态旳分析, 加深对管流不一样流态旳理解。
学习古典流体力学中应用无量纲参数进行试验研究旳措施, 并理解其实用意义。
二、试验原理1.液体在运动时, 存在着两种主线不一样旳流动状态。
当液体流速较小时, 惯性力较小, 粘滞力对质点起控制作用, 使各流层旳液体质点互不混杂, 液流呈层流运动。
当液体流速逐渐增大, 质点惯性力也逐渐增大, 粘滞力对质点旳控制逐渐减弱, 当流速到达一定程度时, 各流层旳液体形成涡体并能脱离原流层, 液流质点即互相混杂, 液流呈紊流运动。
这种从层流到紊流旳运动状态, 反应了液流内部构造从量变到质变旳一种变化过程。
液体运动旳层流和紊流两种型态, 首先由英国物理学家雷诺进行了定性与定量旳证明, 并根据研究成果, 提出液流型态可用下列无量纲数来判断:Re=Vd/νRe称为雷诺数。
液流型态开始变化时旳雷诺数叫做临界雷诺数。
在雷诺试验装置中, 通过有色液体旳质点运动, 可以将两种流态旳主线区别清晰地反应出来。
在层流中, 有色液体与水互不混惨, 呈直线运动状态, 在紊流中, 有大小不等旳涡体振荡于各流层之间, 有色液体与水混掺。
2、在如图所示旳试验设备图中, 取1-1, 1-2两断面, 由恒定总流旳能量方程知:f 2222221111h g2V a p z g 2V a p z ++γ+=+γ+由于管径不变V 1=V 2 ∴=γ+-γ+=)pz ()p z (h 2211f △h 因此, 压差计两测压管水面高差△h 即为1-1和1-2两断面间旳沿程水头损失, 用重量法或体积浊测出流量, 并由实测旳流量值求得断面平均流速 , 作为lghf 和lgv 关系曲线, 如下图所示, 曲线上EC 段和BD 段均可用直线关系式表达, 由斜截式方程得:lgh f =lgk+mlgv lgh f =lgkv m h f =kv m m 为直线旳斜率式中:12ff v lg v lgh lg h lg tg m 12--=θ=试验成果表明EC=1, θ=45°, 阐明沿程水头损失与流速旳一次方成正比例关系, 为层流区。

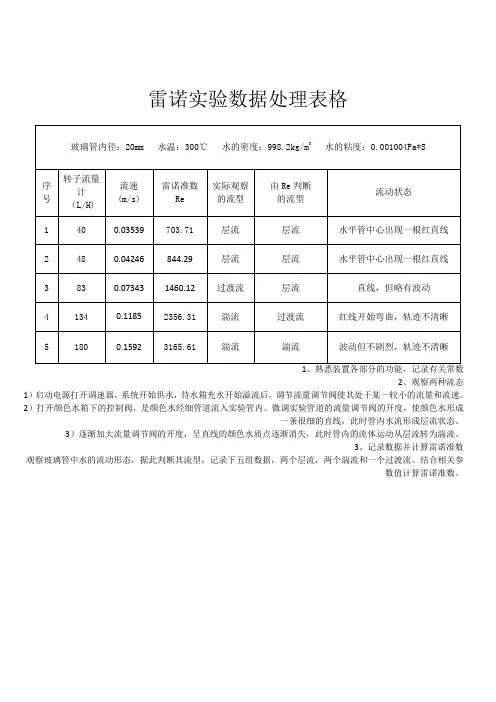
雷诺实验数据处理表格
1、熟悉装置各部分的功能,记录有关常数
2、观察两种流态1)启动电源打开调速器,系统开始供水,待水箱充水开始溢流后,调节流量调节阀使其处于某一较小的流量和流速。
2)打开颜色水箱下的控制阀,是颜色水经细管道流入实验管内。
微调实验管道的流量调节阀的开度,使颜色水形成
一条很细的直线,此时管内水流形成层流状态。
3)逐渐加大流量调节阀的开度,呈直线的颜色水质点逐渐消失,此时管内的流体运动从层流转为湍流。
3、记录数据并计算雷诺准数观察玻璃管中水的流动形态,据此判断其流型,记录下五组数据,两个层流,两个湍流和一个过渡流。
结合相关参
数值计算雷诺准数。

汕 头 大 学 实 验 报 告学院:工学院系:机电系年级:2014级 姓名:成吉祥学号:2014124089 成绩:实验三 雷诺实验一、实验目的1、观察液体的层流、紊流两种流态,掌握圆管流态转化的规律。
2、测定液体在圆管中稳定流动时的上、下临界雷诺数Re c 。
二、实验原理液体在运动时,存在着两种根本不同的流动状态。
当液体流速较小时,惯性力较小,粘滞力对质点起控制作用,使各流层的液体质点互不混杂,液流呈层流运动。
当液体流速逐渐增大,质点惯性力也逐渐增大,粘滞力对质点的控制逐渐减弱,当流速达到一定程度时,各流层的液体形成涡体并能脱离原流层,液流质点即互相混杂,液流呈紊流运动。
这种从层流到紊流的运动状态,反应了液流内部结构从量变到质变的一个变化过程。
在雷诺实验装置中,通过有色液体的质点运动,可以将两种流态的根本区别清晰地反映出来。
在层流中,有色液体与水互不混惨,呈直线运动状态,在紊流中,有大小不等的涡体振荡于各流层之间,有色液体与水混掺。
计算公式:雷诺数 μρdu =Re三、实验注意事项1、每次调节阀门,均需要等待水流稳定几分钟。
2、在关小阀门的过程中,只许渐小,不许开大。
3、随水流量减小,应适当调小开关,以减小溢流量应发的扰动。
四、实验原始数据记录表1 玻璃管内径20毫米,水温21.9℃序号 流量计算值(升/时) 雷诺数 墨水线的形状 1 100 1760 从头到尾都是直线 2 120 2050 从头到尾都是直线 3 140 2500 中部以后有波动 4 160 2800 中部以后有波动 51803230全部有较大波动6 200 3520 全部有较大波动7 240 4250 下部散开8 365 6330 完全湍流9 220 3900 全部有较大波动 10 160 2800 全部有较大波动 111302275从头到尾都是直线表2 玻璃管内径20毫米,水温21.9℃序号 流量计算值(升/时) 雷诺数 墨水线的形状 1 100 1760 从头到尾都是直线 2 120 2050 从头到尾都是直线 3 140 2500 中部以后有波动 4 160 2800 中部以后有波动 5 180 3230 全部有较大波动 6 200 3520 全部有较大波动 7 240 4250 下部散开 8 360 6320 完全湍流 9 220 3900 下部散开 10 180 3230 中部以后有波动 11 160 2800 中部以后有波动 12 155 2725 中部以后有波动 13 150 2650 中部以后有波动 141252162从头到尾都是直线五、实验数据处理 玻璃管内的截面积2421014.34d =A m -⨯=π经过查表可知,在水温为21.9℃时,水的动力粘度为0.9579×10-6 m 2/s 两次测量取平均值(理论值)Re '=2218.5s m mhL /113.01014.3/5.127u 24=⨯=- 此时,计算雷诺数2359109579.01113.002.0Re 6≈⨯⨯⨯==-μρdu 与理论值之间的误差%35.65.22185.22183.2359e R e R Re =-=''-=μ六、个人总结本次雷诺实验测定下临界雷诺数的实验似乎是一个很粗糙实验,通过观察很多个不确定的现象来判定临界位置,但是经过计算之后发现,实验的误差并不大,比想象的其可能的误差要小得多。

学号姓名实验一雷诺实验一、基本原理雷诺(Reynolds)用实验方法研究流体流动时,发现影响流动类型的因素除流速u外,尚有管径(或当量管径)d,流体的密度ρ及粘度μ,并且由此四个物理量组成的无因次数群Re=duρ/μ的值是判定流体流动类型的一个标准。
Re<2000~2300时为层流Re>4000时为湍流2000<Re<4000时为过渡区,在此区间可能为层流,也可能为湍流。
二、设备参数环境参数:温度 20℃压力 101325kPa水的参数:密度 998.2kg/m3 粘度 100.5E-5Pa*s设备参数:玻璃管径:20mm三、实验步骤●打开进水阀门在输入框输入0-100的数字,也可以通过点击上下按钮调节阀门开度。
按回车键完成输入,按ESC 键取消输入。
●打开红墨水阀●打开排水阀门●查看流量点击转子流量计查看当前流体流量●观察流体流动状态点击玻璃管,通过弹出的录像查看流体的流动状态●记录数据点击画面下方的自动记录按钮,记录实验数据,也可以手动记录。
●重复第三步到第六步,记录排水阀不同开度下的流量。
四、数据处理雷诺数计算公式Re=duρ/μ从这个定义式来看,对同一仪器d为定值,故u仅为流量的函数。
对于流体水来说,ρ,μ几乎仅为温度的函数。
因此确定了温度及流量,即可唯一的确定雷诺数。
数据记录:五、注意事项1、雷诺实验要求减少外界干扰,严格要求时应在有避免振动设施的房间内进行,由于条件不具备演示实验也可以在一般房间内进行,因为外界干扰及管子粗细不均匀等原因,层流的雷诺数上界到不了2300,只能到1600左右。
2、层流时红墨水成一线流下,不与水相混。
3、湍流时红墨水与水混旋,分不出界限。

一、实验目的1. 观察流体流动过程中不同的流动形态及其变化过程;2. 测定流动形态变化时的临界雷诺数;3. 理解雷诺数与层流、湍流的关系;4. 掌握实验数据处理方法。
二、实验原理雷诺实验揭示了流体流动的两种基本形态:层流和湍流。
层流是指流体在管道内流动时,流体质点沿直线运动,彼此之间无宏观混合。
湍流则是指流体流动时,流体质点之间发生宏观混合,流速不均匀,产生涡流。
雷诺数(Re)是判断流体流动形态的无量纲数,其计算公式为:Re = ρvd/μ,其中ρ为流体密度,v为流体流速,d为管道直径,μ为流体粘度。
当Re较小时,流体流动为层流;当Re较大时,流体流动为湍流。
临界雷诺数是层流与湍流转变的界限。
三、实验仪器与材料1. 实验装置:自循环雷诺实验装置(包括供水器、实验台、可控硅无级调速器、恒压水箱、有色水水管、稳水隔板、溢流板、实验管道、实验流量调节阀等);2. 实验材料:有色水、清水、压差计、计时器等。
四、实验步骤1. 调整实验装置,确保供水稳定,管道内无气泡;2. 开启供水器,调整流量,使管道内流速逐渐增大;3. 观察有色水在管道内的流动形态,记录下层流、湍流及临界雷诺数;4. 使用压差计测量管道两端的水头差,计算沿程水头损失;5. 记录实验数据,进行数据处理。
五、实验结果与分析1. 观察到当流速较小时,管道内流体质点沿直线运动,颜色均匀,无涡流,为层流;2. 随着流速增大,流体质点开始发生宏观混合,颜色逐渐变淡,出现涡流,为湍流;3. 通过实验,测得临界雷诺数为2000;4. 根据实验数据,绘制沿程水头损失与断面平均流速的关系曲线,分析层流、湍流及临界雷诺数的关系。
六、实验结论1. 雷诺实验验证了流体流动的两种基本形态:层流和湍流;2. 临界雷诺数是层流与湍流转变的界限,本实验测得临界雷诺数为2000;3. 雷诺数与流体流动形态密切相关,当雷诺数较小时,流体流动为层流;当雷诺数较大时,流体流动为湍流。
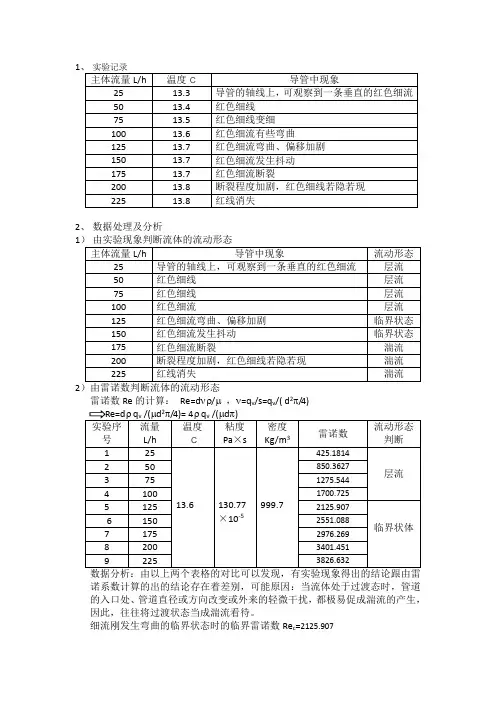

雷诺实验带数据处理.doc雷诺实验(Reynolds Experiment)是19世纪末期的流体力学实验,它的目的是研究液体在直径较小的管道中的流动规律。
这项实验建立了流体力学的一个重要概念——雷诺数(Reynolds Number),它被广泛用于描述流体的运动状态和流动特性。
雷诺实验的数据处理是这个实验的一个重要环节,下面我们将详细介绍雷诺实验的数据处理过程。
一、实验原理雷诺实验的原理是通过调整液体的流量和管道直径来控制雷诺数,观察液体在不同雷诺数下的流动规律,从而获得对液体流动的基本了解。
实验需要用到以下几个参数:1. 流量(Q):指单位时间内流过管道的液体体积。
2. 管道直径(D):液体在管道内的直径。
3. 密度(ρ):液体的质量密度。
根据这些参数,可以计算出雷诺数(Re):Re = (ρDv)/μ其中,v为液体在管道内的平均流速。
根据雷诺数的大小,可以将液体流动分为三个不同的区域:1. 慢流动区:Re<2000。
此时,流体的黏性和惯性力相比较弱,流体的运动状态会受到黏性力的影响,呈现出平滑的层流状态。
2. 过渡区:2000<Re<4000。
此时,流体的惯性力开始增强,液体开始呈现出交替漩涡的纹路。
在这个区域内,液体的流动状态已经开始变得复杂。
3. 快流动区:Re>4000。
此时,液体的惯性力占据主导地位,液体的流动状态呈现出湍流状态。
不规则的漩涡和流体涡流的形成使得液体流动变得非常混乱并且难以预测。
二、实验过程1. 实验器材雷诺实验需要用到管道、放大器、方法罐、压力表和流量计等设备。
其中,管道和放大器是实验的核心设备。
管道带有刻度,可以通过刻度调整管道的直径;放大器可以放大流体的流动状态,方便观察。
2. 实验步骤1)将液体放入方法罐中,打开管道,将液体流入到管道中;2)调整流量计,控制液体的流量;3)通过调整管道直径和流量,控制雷诺数,观察液体的流动状态并记录数据。

一、实验目的1. 观察层流和湍流的流态及其转换特征;2. 通过临界雷诺数,掌握圆管流态判别准则;3. 掌握误差分析在实验数据处理中的应用。
二、实验原理雷诺实验是通过改变管道中的流速,观察流体流动状态的变化,从而研究层流和湍流之间的转换规律。
实验中,流体的流动状态取决于雷诺数(Re),其定义为:\[ Re = \frac{vD}{\nu} \]其中,v为流体的平均流速,D为管道直径,ν为流体的运动粘度。
当雷诺数较小时,流体呈现层流状态;当雷诺数较大时,流体呈现湍流状态。
临界雷诺数(Re_critical)是流体从层流转换为湍流的临界值。
三、实验装置与数据记录实验装置采用自循环雷诺实验装置,主要由供水器、实验台、可控硅无级调速器、恒压水箱、有色水水管、稳水隔板、溢流板、实验管道和实验流量调节阀等组成。
实验过程中,记录以下数据:1. 管径(D):0.02-0.02m;2. 水温:18℃;3. 密度(ρ):998.62kg/m³;4. 粘度(ν):1.053×10⁻³Pa·s;5. 实验次序;6. 流量(Q):通过调节实验流量调节阀得到;7. 流速(v):根据流量和管径计算得到;8. 雷诺数(Re):根据流速、管径和粘度计算得到。
四、数据处理1. 计算不同流量下的流速和雷诺数:\[ v = \frac{Q}{A} \]其中,A为管道截面积,A = πD²/4。
\[ Re = \frac{vD}{\nu} \]2. 绘制流速-雷诺数关系图:以流速为横坐标,雷诺数为纵坐标,绘制流速-雷诺数关系图。
观察曲线,找出临界雷诺数(Re_critical)。
3. 分析实验数据:(1)当雷诺数小于临界雷诺数时,流体呈现层流状态,流速分布均匀,流线平行。
(2)当雷诺数大于临界雷诺数时,流体呈现湍流状态,流速分布不均匀,流线弯曲,出现涡流。
4. 误差分析:(1)实验装置的精度:实验装置的精度会影响实验数据的准确性。
雷诺实验实验报告一、实验目的雷诺实验是研究流体流动形态的重要实验,其主要目的在于:1、观察流体在管内流动时的不同流动形态,即层流和湍流。
2、测定不同流动形态下的雷诺数,以明确雷诺数与流动形态之间的关系。
3、了解如何通过控制实验条件来改变流体的流动形态。
二、实验原理雷诺数(Reynolds Number)是用来判断流体流动形态的无量纲数,其定义为:\Re =\frac{vd\rho}{\mu}\其中,\(v\)为流体的平均流速,\(d\)为管道直径,\(\rho\)为流体密度,\(\mu\)为流体的动力粘度。
当雷诺数小于某一临界值时,流体流动呈层流状态;当雷诺数大于该临界值时,流体流动呈湍流状态。
在实验中,通过调节流量改变流速,同时观察有色液体在管中的流动形态,并测量相应的流量、管径等参数,计算出雷诺数。
三、实验装置本实验所用的雷诺实验装置主要由以下部分组成:1、实验台:提供稳定的支撑和操作平台。
2、玻璃管:作为流体流动的通道,便于观察流动形态。
3、水箱:用于储存和供应实验所需的流体。
4、流量计:测量流体的流量。
5、调节阀:调节流体的流量大小。
6、有色液体注入装置:用于注入有色液体以观察流动形态。
四、实验步骤1、首先,检查实验装置的各个部分是否连接完好,确保无泄漏现象。
2、向水箱中注入适量的水,并开启循环系统,使水在装置中流动,排除管道中的气泡。
3、调节调节阀,使水的流量较小,此时观察有色液体在玻璃管中的流动形态,应为层流。
记录此时的流量、水温等数据。
4、逐渐增大调节阀的开度,增加水的流量,继续观察有色液体的流动形态。
当流动形态发生明显变化,从层流转变为湍流时,记录此时的流量、水温等数据。
5、重复步骤 3 和 4,进行多次测量,以获取更准确的数据。
6、实验结束后,关闭调节阀和循环系统,清理实验装置。
五、实验数据记录与处理以下是一组实验数据记录示例:|实验次数|流量(L/min)|水温(℃)|管径(mm)|平均流速(m/s)|雷诺数|流动形态|||||||||| 1 | 5 | 20 | 20 | 013 | 2600 |层流|| 2 | 10 | 20 | 20 | 027 | 5400 |湍流|| 3 | 8 | 22 | 20 | 021 | 4200 |层流|| 4 | 12 | 22 | 20 | 032 | 6400 |湍流|根据上述数据,计算平均流速和雷诺数的公式如下:平均流速\(v =\frac{Q}{A}\),其中\(Q\)为流量,\(A =\frac{\pi d^2}{4}\)为管道横截面积。
大学教学实验报告实验名称 流管流态实验(雷诺实验) 指导教师 姓名年级学号成绩一、预习部分1. 实验目的 2. 实验基本原理3. 主要仪器设备(含必要的元器件、工具)1、 实验目的:(1) 测定沿程水头损失与断面平均流速的关系,并确定临界雷诺数。
(2) 加深对不同流态的阻力和损失规律的认识。
2、实验基本原理: (1)两个断面的能量方程: 2211221212(12)2g2w gp p hzz γγυυαα-++=+++实验中位均匀流,12υυ= ,12αα=(12)(12)w f h h --=所以水头损失为:121212()()()sin fp p hh h z zαγγ=+-+=-,1h 、2h 为测压牌读数,α为倾斜角。
水力坡度/fJ L h=。
(2)体积法测流量。
/Q W T =, (3)水的粘性系数220.01775(/)10.03370.000221m s t t ν=++,雷诺数Re d υν=3、主要仪器:如图示,另备打气筒、量筒、秒表温度计各一个。
二、实验操作部分1. 实验数据、表格及数据处理 2. 实验操作过程(可用图表示) 3. 结论1. 实验步骤(1)打开水箱下的进水阀向水箱冲水,使水箱有溢水。
再打开管道上的前阀和后阀冲洗水管。
反复开关尾管阀排出空气。
(2)从紊流到层流,将尾阀开到一定开度开始实验,待水流稳定后,测读h 1、h 2、W 、T 。
这样完成一次实验,然后逐步关小尾阀,重复上述步骤,一直做到管流几乎成滴淋状。
(3)再从层流做到紊流。
(此步骤本次实验不做) (4)实验中每半小时测一次水温,取平均值。
(5)对实验数据进行计算分析,以log J 为纵坐标,log v 为横坐标绘制关系曲线,从曲线确定临界流速V k ,并计算雷诺数Re 的值。
并标明实验成果线段坡度,即本次实验的成果。
实验过程注意事项本实验的技术性比较强,每一步操作,都要求实验人员做到精细,才能去的反映真实情况的实验成果。
雷诺实验一、实验目的1.观察层流和紊流的流动特征及其转变情况,加深对层流、紊流形态的感性认识。
2.测定层流与紊流的雷诺数。
二、实验原理在圆管流动中采用雷诺数来判别流态:νvd=Re 式中:v 一圆管水流的断面平均流速;d 一圆管直径;υ一水流的运动粘滞系数。
当Re<Rec(下临界雷诺数)时为层流状态,Rec<2320。
当Re<Rec`(上临界雷诺数)时为紊流状态,Rec`在4000—12000之间。
三、实验装置图实验装置图如下图1图1 雷诺实验装置图1.自循环供水器 2.实验台 3.可控硅无级调速器 4.恒压水箱5.有色水水管 6.稳水孔板 7.溢流板 8.实验管道9.实验流量调节阀 10.压强水位计供水流量由9调控,使恒压水箱4始终保持微溢流的状态,以提高进口前水体稳定程度。
本恒压水箱还设有多道稳水隔板,可使稳水时间缩短到3~5分钟。
四、实验步骤1.观察流动形态将进水管打开使水箱冲水,并保持溢流状态;然后用尾部阀门调节流量,将阀门微微打开,2.测定hf~v 的关系及临界雷诺数 (1)熟悉仪器,测记有关常数。
(2)检查尾阀全关时,压差计液面是否齐平,若不平,则需排气调平。
(3)将尾部阀门开至最大,然后逐步关小阀门,使管内流量逐步减少;每改变一次流量,均待水流平稳后,测定每次的流量、水温和试验段的水头损失(即压差)。
流量Q 用体积法测量。
用量筒量测水的体积V ,用秒表计时间T 。
流量Q=T V 。
相应的断面平均流速v=AQ。
(4)流量用尾阀调节,共做10次。
当Re<2500时,为精确起见,每次压差减小值只能为3~5mm 。
(5)用温度计量测当日的水温,由此可查得运动粘滞系数υ,从而计算雷诺数νvd=Re 。
(6)相反,将调节阀由小逐步开大,管内流速慢慢加大,重复上述步骤。
五、注意事项1、在整个试验过程中,要特别注意保持水箱内的水头稳定。
每变动一次阀门开度,均待水头稳定后再量测流量和水头损失。
雷诺实验报告
实验目的:通过雷诺实验测量流体在管道中的湍流转捩临界雷诺数。
实验原理:当流体在管道内流动时,当流速不断增大时,原本属于层流状态的流动会发生转捩,并出现湍流现象。
雷诺实验是通过改变流体流过管道的速度,观察流动状态的变化来测量流体的转捩临界雷诺数。
实验仪器与装置:雷诺实验装置包括一个立式水管,水泵,流量调节阀,流量计,压力表等。
实验步骤:
1. 打开水泵,调节流量调节阀,使水流通过管道。
2. 逐渐增加水泵的工作压力,调节流量调节阀,使水流速度逐渐增大。
3. 当水流进入管道后,观察水流的状态。
当水流呈现湍流时,记录此时的流速,并记为临界雷诺数。
4. 重复上述步骤,进行多次实验,取平均值。
实验数据处理与分析:根据实验得到的数据,计算出多次实验的平均流速,并确定转捩临界雷诺数。
分析实验结果与理论值的差异,并对实验误差和影响因素进行讨论。
实验结论:根据实验结果,得出流体在管道中的湍流转捩临界雷诺数。
讨论实验误差和影响因素,并提出改进实验方法的建议。
汕 头 大 学 实 验 报 告学院:工学院系:机电系年级:2014级 姓名:成吉祥学号:2014124089 成绩:实验三 雷诺实验一、实验目的1、观察液体的层流、紊流两种流态,掌握圆管流态转化的规律。
2、测定液体在圆管中稳定流动时的上、下临界雷诺数Re c 。
二、实验原理液体在运动时,存在着两种根本不同的流动状态。
当液体流速较小时,惯性力较小,粘滞力对质点起控制作用,使各流层的液体质点互不混杂,液流呈层流运动。
当液体流速逐渐增大,质点惯性力也逐渐增大,粘滞力对质点的控制逐渐减弱,当流速达到一定程度时,各流层的液体形成涡体并能脱离原流层,液流质点即互相混杂,液流呈紊流运动。
这种从层流到紊流的运动状态,反应了液流内部结构从量变到质变的一个变化过程。
在雷诺实验装置中,通过有色液体的质点运动,可以将两种流态的根本区别清晰地反映出来。
在层流中,有色液体与水互不混惨,呈直线运动状态,在紊流中,有大小不等的涡体振荡于各流层之间,有色液体与水混掺。
计算公式:雷诺数 μρdu =Re三、实验注意事项1、每次调节阀门,均需要等待水流稳定几分钟。
2、在关小阀门的过程中,只许渐小,不许开大。
3、随水流量减小,应适当调小开关,以减小溢流量应发的扰动。
四、实验原始数据记录表1 玻璃管内径20毫米,水温21.9℃序号 流量计算值(升/时) 雷诺数 墨水线的形状 1 100 1760 从头到尾都是直线 2 120 2050 从头到尾都是直线 3 140 2500 中部以后有波动 4 160 2800 中部以后有波动 51803230全部有较大波动6 200 3520 全部有较大波动7 240 4250 下部散开8 365 6330 完全湍流9 220 3900 全部有较大波动 10 160 2800 全部有较大波动 111302275从头到尾都是直线表2 玻璃管内径20毫米,水温21.9℃序号 流量计算值(升/时) 雷诺数 墨水线的形状 1 100 1760 从头到尾都是直线 2 120 2050 从头到尾都是直线 3 140 2500 中部以后有波动 4 160 2800 中部以后有波动 5 180 3230 全部有较大波动 6 200 3520 全部有较大波动 7 240 4250 下部散开 8 360 6320 完全湍流 9 220 3900 下部散开 10 180 3230 中部以后有波动 11 160 2800 中部以后有波动 12 155 2725 中部以后有波动 13 150 2650 中部以后有波动 141252162从头到尾都是直线五、实验数据处理 玻璃管内的截面积2421014.34d =A m -⨯=π经过查表可知,在水温为21.9℃时,水的动力粘度为0.9579×10-6 m 2/s 两次测量取平均值(理论值)Re '=2218.5s m mhL /113.01014.3/5.127u 24=⨯=- 此时,计算雷诺数2359109579.01113.002.0Re 6≈⨯⨯⨯==-μρdu 与理论值之间的误差%35.65.22185.22183.2359e R e R Re =-=''-=μ六、个人总结本次雷诺实验测定下临界雷诺数的实验似乎是一个很粗糙实验,通过观察很多个不确定的现象来判定临界位置,但是经过计算之后发现,实验的误差并不大,比想象的其可能的误差要小得多。
雷诺实验
一、实验目的
1. 观察层流和紊流的流态及其转换特征。
2. 通过临界雷诺数,掌握圆管流态判别准则。
3. 掌握误差分析在实验数据处理中的应用。
二、实验原理
1、实际流体的流动会呈现出两种不同的型态:层流和紊流,它们的区别在于:流动过程中流体层之间是否发生混掺现象。
在紊流流动中存在随机变化的脉动量,而在层流流动中则没有,如图1所示。
2、圆管中恒定流动的流态转化取决于雷诺数。
雷诺根据大量实验资料,将影响流体流动状态的因素归纳成一个无因次数,称为雷诺数Re ,作为判别流体流动状态的准则
4Re Q
D πυ
=
式中 Q ——流体断面平均流量 , L s
D ——圆管直径 , mm
υ——流体的运动粘度 , 2m s
在本实验中,流体是水。
水的运动粘度与温度的关系可用泊肃叶和斯托克斯提出的经验公式计算
36((0.58510(T 12)0.03361)(T 12) 1.2350)10υ--=⨯⨯--⨯-+⨯ 式中 υ——水在t C ︒时的运动粘度,2m s ; T ——水的温度,C ︒。
3、判别流体流动状态的关键因素是临界速度。
临界速度随流体的粘度、密
度以及流道的尺寸不同而改变。
流体从层流到紊流的过渡时的速度称为上临界流速,从紊流到层流的过渡时的速度为下临界流速。
4、圆管中定常流动的流态发生转化时对应的雷诺数称为临界雷诺数,对应于上、下临界速度的雷诺数,称为上临界雷诺数和下临界雷诺数。
上临界雷诺数表示超过此雷诺数的流动必为紊流,它很不确定,跨越一个较大的取值围。
而且极不稳定,只要稍有干扰,流态即发生变化。
上临界雷诺数常随实验环境、流动的起始状态不同有所不同。
因此,上临界雷诺数在工程技术中没有实用意义。
有实际意义的是下临界雷诺数,它表示低于此雷诺数的流动必为层流,有确定的取值。
通常均以它作为判别流动状态的准则,即
Re < 2320 时,层流
Re > 2320 时,紊流
该值是圆形光滑管或近于光滑管的数值,工程实际中一般取Re = 2000。
5、实际流体的流动之所以会呈现出两种不同的型态是扰动因素与粘性稳定作用之间对比和抗衡的结果。
针对圆管中定常流动的情况,容易理解:减小D ,减小 ,加大v 三种途径都是有利于流动稳定的。
综合起来看,小雷诺数流动趋于稳定,而大雷诺数流动稳定性差,容易发生紊流现象。
6、由于两种流态的流场结构和动力特性存在很大的区别,对它们加以判别并分别讨论是十分必要的。
圆管中恒定流动的流态为层流时,沿程水头损失与平均流速成正比,而紊流时则与平均流速的1.75~2.0次方成正比,如图2所示。
7、通过对相同流量下圆管层流和紊流流动的断面流速分布作一比较,可以看出层流流速分布呈旋转抛物面,而紊流流速分布则比较均匀,壁面流速梯度和切应力都比层流时大,如图3所示。
紊流流速分布
层流流速分布
图1 三种流态示意 图2 三种流态曲线 图3 圆管断面流速分布
三、实验装置
四、实验数据分析
有关常数:管径 d = 30 mm , 水温 T = 27 ℃,
运动粘性系数:v =78.6247510-⨯m 2/s
表1 数据记录表格
项目 测
次
流量(L/h) 温度(℃) 雷诺数(Re) 误差 颜色水形态 上临界雷诺数 1 277 26.8 3786 39.26%
完全散开 上临界雷诺数 2 268 27 3663 37.22%
完全散开 上临界雷诺数
3 277 27 3786 39.26%
完全散开
注:颜色水形态指:稳定直线,稳定略弯曲,直线摆动,直线抖动,断续,完全散开等。
三次测量取平均值,可得下临界雷诺数为Re 2200=,与公认值Re 2300=相比,可得误差为
23002200
100% 4.348%2300
δ-=
⨯=
五、误差分析
运动粘度偏差公式
T T T T
∆----=∆∂∂=
∆*)6(^10*]03361.0)3(^10*585.0*)242[(*ν
ν 求得水流的运动粘度的偏差为:
ν∆= 62[(2*2724)*0.585*10^(3)0.03361]*10^(6)*00.001410/.1m s -=-⨯--- 即:6620.8625100.001410/m s ν--=⨯±⨯
由流量公式:Q
Q t t
∂∆=
⨯∆∂ 由流量公式:Q=A*v 可求得: 流速公式为:v=Q/A=4Q/(πD 2)
雷诺数公式为:Re=4Q/(πD ν) 雷诺数的偏差公式为:
∆Re= νν∆∂∂+∆∂∂*Re
*Re Q Q =νν
πνπ∆+∆*4*42
D Q
Q D
根据以上公式,可分别求得三组数据所对应的未知量: 1.对于第一组数据:
=0.11153=16.83/Q L h ∆⨯ 1(15316.83)L/h Q =±
20.1890.021/m s ν=±
(141209)2Re Q D πν=⨯÷=
1230Re ∆=
雷诺数的相对误差为:1Re Re
100%9.98%Re
δ'-=⨯= 2.对于第二组数据:
=0.11174=19.14/Q L h ∆⨯ 1(17419.14)L/h Q =±
20.2150.022/m s ν=±
(141237)8Re Q D πν=⨯÷=
1262Re ∆=
雷诺数的相对误差为:2Re Re
100% 3.30%Re
δ'-=⨯=
3.对于第三组数据:
=0.11156=17.16/Q L h ∆⨯ 1(15617.16)L/h Q =±
20.1930.021/m s ν=±
(141213)2Re Q D πν=⨯÷=
1235Re ∆=
雷诺数的相对误差为:1Re Re
100%7.86%Re
δ'-=
⨯=
以上三组数据所求得的雷诺数的相对误差均处于误差允许围,所以可认为实验测得数据合理有效。
误差来源 1、仪器误差
使用2L 量筒以及秒表测量出水口处流量,约为240L/h ,此时仪器显示
270L/h ,计算误差,有
30
Q 11%270
Q Q ∆→
== , Q 16117.71/h Q Q L =±∆=± T=270.1C o T T ±∆=±
Re 2200234=± 仪器误差是主要误差
2、人为误差
由于上下临界雷诺数的判定是由人眼观察管中红墨水线的形态判断,所以在判断过程中会有些许误差,这些误差体现在流量中。
即,对于临界状态的判断会
影响最后对流量值得记录,导致雷诺数产生误差,这是不可避免的误差。
3、外部环境影响
受到桌面振动等影响会对实验造成一定的误差,在实验过程中已经力求避免这样的误差。
六、分析思考问题
1、层流、紊流两种水流流态的外观表现是怎样的?
答:层流:质点有规律地作分层流动,管颜色水成一股细直的流束,运动要素无脉动现象。
紊流:质点互相混渗作无规则运动,管颜色水成直线抖动、断续或是完全散开,最终与周围清水迅速相混,运动要素发生不规则的脉动现象
2、雷诺数的物理意义是什么?为什么雷诺数可以用来判别流态?
答:雷诺数物理意义:惯性力与粘性力之比,是表征流动状态的一个无因次数。
层流:流体质点一直沿流线运动,彼此平行,不发生相互混杂的流动。
紊流:流体质点在运动过程中,互相混杂、穿插的流动。
(紊流包含,主体流动+各种大小强弱不同的旋涡)因层流与紊流所处的状态不同,故数值大小也不同,所以可以用雷诺数来差别流态,数值大于临界值的为紊流,小于临界值的为层流。
3、临界雷诺数与哪些因素有关?为什么上临界雷诺数和下临雷诺数不一样?答:临界雷诺数与流速、管径、流体的动力粘度及流体的密度有关。
上临界雷诺数和下临雷诺数之所以不一样是因为混乱无章的流动所具有的惯性力大于层流的粘性力;当从层流变成紊流时,粘性力逐渐减小,惯性力逐渐增大,因为不同的力所主导的作用不一样,所以上临界雷诺数和下临雷诺数不一样。
4、流态判据为何采用无量纲参数,而不采用临界流速?
答:流速只能代表惯性力。
雷诺数是惯性力与粘性力之比。
判断一个流态是层流还是湍流要看它的雷诺数是否超过临界雷诺数。
只看速度是不够的,比如两个相同速度的流动,一个在光滑的管进行,一个在粗糙的管进行,则光滑管中的可能保持为层流,而粗糙管中的可能已是湍流。
可见速度并不能说明问题的实质。
5、破坏层流的主要物理原因是什么?
答:是流体质点掺混,互相碰撞所造成的惯性阻力作用大于粘性力作用,因此而导致层流的破坏。