雷诺实验数据处理表格

雷诺实验实验人：09335004 王宗谭一、实验目的要求1．观察层流、紊流的流态及其转换特征；2．测定下临界雷诺数，掌握圆管流态判别准则；3．掌握误差分析在实验数据处理中的应用。

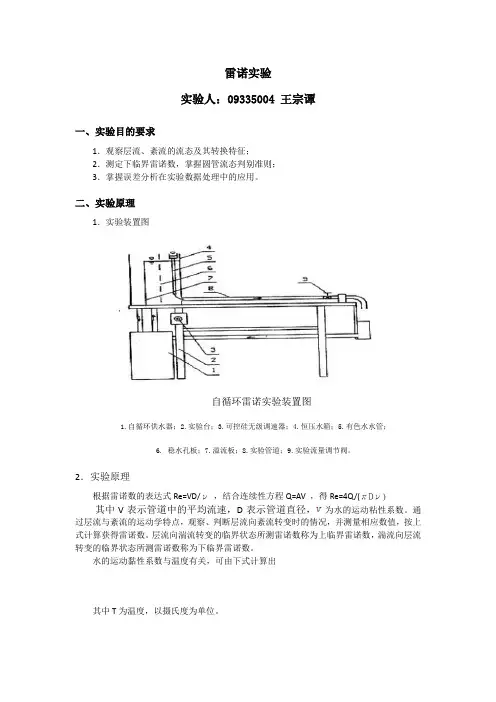
二、实验原理1．实验装置图自循环雷诺实验装置图1.自循环供水器；2.实验台；3.可控硅无级调速器；4.恒压水箱；5.有色水水管；6. 稳水孔板；7.溢流板；8.实验管道；9.实验流量调节阀。

2．实验原理根据雷诺数的表达式Re=VD/ν，结合连续性方程Q=AV ，得Re=4Q/(πDν)其中V表示管道中的平均流速，D表示管道直径，为水的运动粘性系数。

通过层流与紊流的运动学特点，观察、判断层流向紊流转变时的情况，并测量相应数值，按上式计算获得雷诺数。

层流向湍流转变的临界状态所测雷诺数称为上临界雷诺数，湍流向层流转变的临界状态所测雷诺数称为下临界雷诺数。

水的运动黏性系数与温度有关，可由下式计算出其中T为温度，以摄氏度为单位。

三、实验方法与步骤1．测记本实验的有关常数。

2．观察两种流态。

打开开关3使水箱充水至溢流水位，经稳定后，微微开启调节阀9，并注入颜色水于实验管内，使颜色水流成一直线。

通过颜色水质点的运动观察管内水流的层流流态，然后逐步开大调节阀，通过颜色水直线的变化观察层流转变到紊流的水力特征，待管中出现完全紊流后，再逐步关小调节阀，观察由紊流转变为层流的水力特征。

3．测定下临界雷诺数。

(1)将调节阀打开，使管中呈完全紊流，再逐步关小调节阀使流量减小。

当流量调节到使颜色水在全管刚呈现出一稳定直线时，即为下临界状态；(2)待管中出现临界状态时，用体积法测定流量；(3)根据所测流量计算下临界雷诺数，并与公认值（2300）比较，偏离过大，需重测；(4)重新打开调节阀，使其形成完全紊流，按照上述步骤重复测量不少于三次；(5)同时用水箱中的温度计测记水温，从而求得水的运动粘度。

[注意](1)每调节阀门一次，均需等待稳定几分钟；(2)关小阀门过程中，只许渐小，不许开大；(3)随出水流量减小，应适当调小开关，以减小溢流量引发的扰动。

一、实验目的1. 了解雷诺方程的基本原理和应用；2. 掌握雷诺方程的求解方法；3. 通过实验验证雷诺方程的正确性。

二、实验原理雷诺方程是描述流体运动的一种偏微分方程，它是由英国物理学家奥斯本·雷诺（Osborne Reynolds）于1883年提出的。

雷诺方程可以描述流体在层流和湍流状态下的运动规律。

雷诺方程的基本形式如下：$\frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla)\mathbf{u} = -\frac{1}{\rho} \nabla p + \nu \nabla^2 \mathbf{u}$其中，$\mathbf{u}$表示流体的速度矢量，$p$表示流体的压力，$\rho$表示流体的密度，$\nu$表示流体的运动粘度。

三、实验装置1. 实验台：用于放置实验器材；2. 流体水箱：用于盛装流体；3. 流量计：用于测量流体流量；4. 流速传感器：用于测量流体速度；5. 压力传感器：用于测量流体压力；6. 数据采集系统：用于采集实验数据。

四、实验步骤1. 将实验装置安装好，确保各部件连接牢固；2. 将流体倒入水箱，调整流量计，使流体流量稳定；3. 通过流速传感器和压力传感器采集流体速度和压力数据；4. 将采集到的数据输入数据采集系统，进行数据处理和分析；5. 根据实验数据，验证雷诺方程的正确性。

五、实验数据1. 流体流量：$Q = 0.2 \text{ m}^3/\text{s}$；2. 流体密度：$\rho = 1000 \text{ kg/m}^3$；3. 流体运动粘度：$\nu = 1.0 \times 10^{-6} \text{ m}^2/\text{s}$；4. 流体速度：$u = 0.5 \text{ m/s}$；5. 流体压力：$p = 1.0 \times 10^5 \text{ Pa}$。

大学教学实验报告实验名称 流管流态实验（雷诺实验） 指导教师 姓名年级学号成绩一、预习部分1． 实验目的 2． 实验基本原理3． 主要仪器设备（含必要的元器件、工具）1、 实验目的：（1） 测定沿程水头损失与断面平均流速的关系，并确定临界雷诺数。

（2） 加深对不同流态的阻力和损失规律的认识。

2、实验基本原理： （1）两个断面的能量方程： 2211221212(12)2g2w gp p hzz γγυυαα-++=+++实验中位均匀流，12υυ= ，12αα=(12)(12)w f h h --=所以水头损失为：121212()()()sin fp p hh h z zαγγ=+-+=-，1h 、2h 为测压牌读数，α为倾斜角。

水力坡度/fJ L h=。

（2）体积法测流量。

/Q W T =， （3）水的粘性系数220.01775(/)10.03370.000221m s t t ν=++，雷诺数Re d υν=3、主要仪器：如图示，另备打气筒、量筒、秒表温度计各一个。

二、实验操作部分1． 实验数据、表格及数据处理 2． 实验操作过程（可用图表示） 3． 结论1. 实验步骤（1）打开水箱下的进水阀向水箱冲水，使水箱有溢水。

再打开管道上的前阀和后阀冲洗水管。

反复开关尾管阀排出空气。

（2）从紊流到层流，将尾阀开到一定开度开始实验，待水流稳定后，测读h 1、h 2、W 、T 。

这样完成一次实验，然后逐步关小尾阀，重复上述步骤，一直做到管流几乎成滴淋状。

（3）再从层流做到紊流。

（此步骤本次实验不做） （4）实验中每半小时测一次水温，取平均值。

（5）对实验数据进行计算分析，以log J 为纵坐标，log v 为横坐标绘制关系曲线，从曲线确定临界流速V k ，并计算雷诺数Re 的值。

并标明实验成果线段坡度，即本次实验的成果。

实验过程注意事项本实验的技术性比较强，每一步操作，都要求实验人员做到精细，才能去的反映真实情况的实验成果。

化工原理雷诺实验报告篇一：化工原理实验报告(流体阻力)摘要：本实验通过测定流体在不同管路中流动时的流量qv、测压点之间的压强差ΔP，结合已知的管路的内径、长度等数据，应用机械能守恒式算出不同管路的λ‐Re变化关系及突然扩大管的?-Re关系。

从实验数据分析可知，光滑管、粗糙管的摩擦阻力系数随Re增大而减小，并且光滑管的摩擦阻力系数较好地满足Blasuis关系式：?? 。

突然扩大管的局部阻力系数随Re的变化而变化。

一、目的及任务①掌握测定流体流动阻力实验的一般实验方法。

②测定直管的摩擦阻力系数λ及突然扩大管和阀门的局部阻力系数ξ。

③验证湍流区内摩擦系数λ为雷诺数Re 和相对粗糙度的函数。

④将所得光滑管λ-Re方程与Blasius方程相比较。

二、基本原理1. 直管摩擦阻力不可压缩流体，在圆形直管中做稳定流动时，由于黏性和涡流的作用产生摩擦阻力；流体在流过突然扩大、弯头等管件时，由于流体运动的速度和方向突然变化，产生局部阻力。

影响流体阻力的因素较多，在工程上通常采用量纲分析方法简化实验，得到在一定条件下具有普遍意义的结果，其方法如下：流体流动阻力与流体的性质，流体流经处的几何尺寸以及流动状态相关，可表示为：△p=?(d,l,u,ρ, μ, ε) 引入下列无量纲数群。

雷诺数 Re?相对粗糙度管子长径比从而得到lddu???d??(du??l,,) ?dd?p?u2令???(Re,)d??p??ld?(Re,?ud)22可得到摩擦阻力系数与压头损失之间的关系，这种关系可用实验方法直接测定。

hf??p???ld?u22式中hf——直管阻力，J/kg；——被测管长，m； d——被测管内径，m； u——平均流速，m/s； ?——摩擦阻力系数。

当流体在一管径为d的圆形管中流动时，选取两个截面，用U形压差计测出这两个截面间的静压强差，即为流体流过两截面间的流动阻力。

根据伯努利方程找出静压强差和摩擦阻力系数的关系式，即可求出摩擦阻力系数。

实验四 流动状态实验----雷诺实验一、实验目的1. 观察层流和紊流的流态及其转换特征;2. 通过临界雷诺数，掌握圆管流态判别准则;3. 学习在流体力学中应用无量纲参数进行试验研究的方法，并了解其使用意义。

二、实验原理1、实际流体的流动会呈现出两种不同的型态：层流和紊流，它们的区别在于：流动过程中流体层之间是否发生混掺现象。

在紊流流动中存在随机变化的脉动量，而在层流流动中则没有，如图1所示。

2、圆管中恒定流动的流态转化取决于雷诺数。

雷诺根据大量实验资料，将影响流体流动状态的因素归纳成一个无因次数，称为雷诺数Re ，作为判别流体流动状态的准则Re d υγ=式中 υ——流体断面平均流速 , s cm d ——圆管直径 , cmγ——流体的运动粘度 , cm 2在本实验中，流体是水。

水的运动粘度与温度的关系可用泊肃叶和斯托克斯提出的经验公式计算20.017810.03370.000221t tγ=++ 式中γ——水在t C ︒时的运动粘度，s cm 2；t ——水的温度，C ︒。

3、判别流体流动状态的关键因素是临界速度。

临界速度随流体的粘度、密度以及流道的尺寸不同而改变。

流体从层流到紊流的过渡时的速度称为上临界流速，从紊流到层流的过渡时的速度为下临界流速。

4、圆管中定常流动的流态发生转化时对应的雷诺数称为临界雷诺数，对应于上、下临界速度的雷诺数，称为上临界雷诺数和下临界雷诺数。

上临界雷诺数表示超过此雷诺数的流动必为紊流，它很不确定，跨越一个较大的取值范围。

而且极不稳定，只要稍有干扰，流态即发生变化。

上临界雷诺数常随实验环境、流动的起始状态不同有所不同。

因此，上临界雷诺数在工程技术中没有实用意义。

有实际意义的是下临界雷诺数，它表示低于此雷诺数的流动必为层流，有确定的取值。

通常均以它作为判别流动状态的准则，即Re < 2320 时，层流 Re > 2320 时，紊流该值是圆形光滑管或近于光滑管的数值，工程实际中一般取Re = 2000。

一、实验目的1. 了解雷诺数的基本概念及其在流体力学中的应用。

2. 观察流体在不同雷诺数下的流动特性，包括层流和湍流。

3. 掌握通过改变雷诺数来控制流体流动状态的方法。

4. 学习实验数据处理和分析方法。

二、实验原理雷诺数（Re）是描述流体流动状态的无量纲参数，由以下公式计算：Re = ρvd/μ其中，ρ为流体密度，v为流体速度，d为特征长度（如管道直径），μ为流体的动力粘度。

根据雷诺数的大小，流体流动可分为层流和湍流两种状态。

当雷诺数较小时，流体流动呈现层流状态；当雷诺数较大时，流体流动呈现湍流状态。

三、实验装置与仪器1. 实验装置：雷诺演示实验装置，包括实验管道、水泵、流量计、阀门等。

2. 仪器：温度计、秒表、直尺、量筒等。

四、实验步骤1. 调整实验装置，连接好实验管道、水泵、流量计等。

2. 将实验管道充满清水，关闭阀门，使系统稳定。

3. 通过调节水泵的转速，改变流体速度，记录不同速度下的流量。

4. 测量实验管道的特征长度，计算不同速度下的雷诺数。

5. 观察流体在不同雷诺数下的流动状态，记录层流和湍流的转变过程。

6. 对实验数据进行处理和分析，绘制雷诺数与流速、流量等参数的关系曲线。

五、实验结果与分析1. 实验数据根据实验数据，绘制了雷诺数与流速、流量等参数的关系曲线，如下：（此处插入实验数据关系曲线图）2. 分析（1）层流状态：当雷诺数较小时，流体流动呈现层流状态。

此时，流体在管道内呈平行层状流动，流速分布均匀，流动稳定。

（2）湍流状态：当雷诺数较大时，流体流动呈现湍流状态。

此时，流体在管道内呈现涡旋、湍流等现象，流速分布不均匀，流动不稳定。

（3）层流与湍流的转变：当雷诺数达到一定值时，流体流动状态会发生转变。

这个转变值称为临界雷诺数。

在本实验中，临界雷诺数约为2100。

（4）雷诺数与流速、流量等参数的关系：从实验数据关系曲线可以看出，随着流速的增加，雷诺数也随之增加。

当流速超过临界雷诺数时，流体流动状态由层流转变为湍流。