第4章 变形率和旋率
- 格式:doc
- 大小:420.50 KB
- 文档页数:7
第四章 流体的有旋流动和无旋流动在上一章中我们阐述了流体流动的一些基本概念,导出了流体流动的连续性方程、欧拉运动方程、伯努利方程和动量方程等,为解决工程实际问题奠定了一定的理论基础。
本章将进一步讨论流体的有旋流动和无旋流动。
第一节 流体微团运动的分析我们知道,刚体的运动一般可以分解为移动和转动两部分。
但流体与刚体不同,流体受力便会发生运动状态的变化,即流体具有流动性,极易变形。
因此,流体微团在运动过程中不但会发生移动和转动,而且还会发生变形运动。
所以,在一般情况下流体微团的运动可以分解为移动、转动和变形运动三部分。
变形运动又分为线变形运动和角变形运动两种情况。
下面我们分别讨论这几种运动情况。
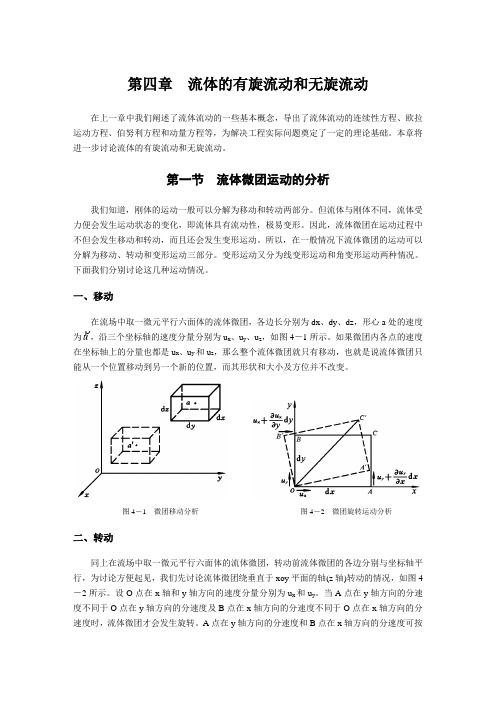
一、移动在流场中取一微元平行六面体的流体微团,各边长分别为dx 、dy 、dz ,形心a 处的速度为u,沿三个坐标轴的速度分量分别为u x 、u y 、u z ,如图4-1所示。
如果微团内各点的速度在坐标轴上的分量也都是u x 、u y 和u z ,那么整个流体微团就只有移动,也就是说流体微团只能从一个位置移动到另一个新的位置,而其形状和大小及方位并不改变。
图4-1 微团移动分析4-2 微团旋转运动分析二、转动同上在流场中取一微元平行六面体的流体微团,转动前流体微团的各边分别与坐标轴平行,为讨论方便起见,我们先讨论流体微团绕垂直于xoy 平面的轴(z 轴)转动的情况,如图4-2所示。
设O 点在x 轴和y 轴方向的速度分量分别为u x 和u y 。
当A 点在y 轴方向的分速度不同于O 点在y 轴方向的分速度及B 点在x 轴方向的分速度不同于O 点在x 轴方向的分速度时,流体微团才会发生旋转。
A 点在y 轴方向的分速度和B 点在x 轴方向的分速度可按泰勒级数展开,并略去高阶无穷小量而得到,它们分别为x xu u d y y ∂∂+和y yu u d xx ∂∂+,它们相对于O 点的对应分速度(相对于O 点的线速度)分别为x xu d y ∂∂和y yu d x∂∂,所以它们相对于O 点的角速度(逆时针方向旋转为正)应为A 点上xu x x xu ∂∂=∂∂y y d /dB 点上 yuy y y u ∂∂-=∂∂-x x d /d 而对于微团中其它各点绕z 轴转动的角速度(如C 点等)则是由该点y 向的分速度在x 轴方向的变化量和x 向的分速度在y 轴方向的变化量共同产生的。
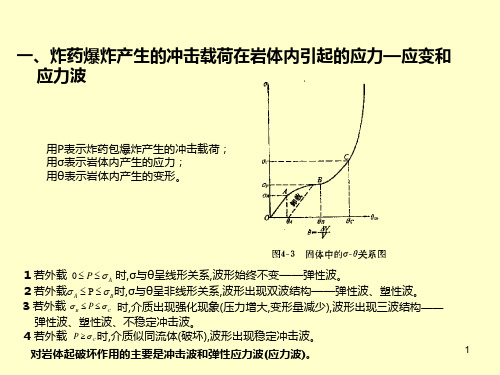




五、岩石的蠕变1、蠕变特征①岩石蠕变的概念在应力不变的情况下,岩石变形随时间t 而增长的现象。
即 d 随时间而变化。
σdt②岩石蠕变类型有两种类型:稳定型蠕变ε非稳定型蠕变a 、 稳定型蠕变 :在恒定εⅡ应力作用下,变形速率Ⅰ随时间递减,最终趋于Ⅰ零,即d0 ,变形区dtt域稳定。
一般在较小应力下或硬岩中。
b 、 非稳定型蠕变 :岩石在恒定应力作用下,岩石变形随时间不断增 长,直至破坏。
一般为软弱岩石或应力较大。
③蠕变曲线变化特征岩石的蠕变曲线可分为三个阶段:Ⅰ阶段:初期蠕变。
应变-时间曲线向下弯曲,应变速率d由大变dt小。
属弹性变形。
Ⅱ阶段:等速蠕变。
εⅢⅡⅠTCBP UA VεQeR0 t应变-时间曲线近似直线,应变随时间呈近于等速增长。
出现塑性。
Ⅲ阶段:加速蠕变。
应变-时间曲线向上弯曲,其应变速率加快直至破坏。
应指出,并非所有的蠕变都能出现等速蠕变阶段,只有蠕变过程中结构的软化和硬化达到动平衡,蠕变速率才能保持不变。
在Ⅰ阶段,如果应力骤降到零,则-t 曲线具有 PQR形式,曲线从 P 点骤变到 Q 点,PQ=e为瞬时弹性变形,而后随时间慢慢退到应变为零,这时无永久变形,材料仍保持弹性。
在Ⅱ阶段,如果把应力骤降到零,则会出现永久变形,其中TU=e。
④不同应力下的蠕变岩石蠕变速率与应力大小有直接关系。
低应力时,应变速度变化缓慢,逐渐趋于稳定。
应力增大时,应变速率增大。
高应力时,蠕变加速,直至破坏。
应力越大,蠕变速率越大,反之愈小。
b bε2520 b1815 b10baa a-稳定蠕变 ( 不破坏)tb-非稳定蠕变( 蠕变破坏)岩石长期强度:指岩石由稳定蠕变转为非稳定蠕变时的应力分界值。
即,岩石在长期荷载作用下经蠕变破坏的最小应力值(或)岩石极限长期强度:指长期荷载作用下岩石的强度。
2、蠕变经验公式由于岩石蠕变包括瞬时弹性变形、初始蠕变、等速蠕变和加速蠕变,则在荷载长期作用下,岩石蠕变的变形可用经验公式表示为:=e + (t) +M t + T(t )e-瞬时变形;(t ) -初始蠕变; M t-等速蠕变;T (t )-加速蠕变。
流体力学总结第一章流体及其物理性质1. 流体:流体是一种受任何微小剪切力作用都能连续变形的物质,只要这种力继续作用,流体就将继续变形,直到外力停顿作用为止。
流体一般不能承受拉力,在静止状态下也不能承受切向力,在任何微小切向力的作用下,流体就会变形,产生流动 2. 流体特性:易流动(易变形)性、可压缩性、粘性 3. 流体质点:宏观无穷小、微观无穷大的微量流体。
4. 流体连续性假设:流体可视为由无数连续分布的流体质点组成的连续介质。
稀薄空气和激波情况下不适合。
5. 密度0limV m m V V δδρδ→==重度0lim V G Gg V Vδδγρδ→===比体积1v ρ=6. 相对密度:是指*流体的密度与标准大气压下4︒C 时纯水的密度〔1000〕之比w wS ρρρ=为4︒C 时纯水的密度13.6Hg S = 7. 混合气体密度1ni ii ρρα==∑8. 体积压缩系数:温度不变,单位压强增量引起的流体体积变化率。
体积压缩系数的倒数为体积模量1P PK β=9. 温度膨胀系数:压强不变,单位温升引起的流体体积变化率。
10. 不可压缩流体:流体受压体积不减少,受热体积不膨胀,密度保持为常数,液体视为不可压缩流体。
气体流速不高,压强变化小视为不可压缩流体 11. 牛顿内摩擦定律:du dyτμ=黏度du dyτμ=流体静止粘性无法表示出来,压强对黏度影响较小,温度升高,液体黏度降低,气体黏度增加μυρ=。
满足牛顿内摩擦定律的流体为牛顿流体。
12. 理想流体:黏度为0,即0μ=。
完全气体:热力学中的理想气体第二章流体静力学1. 外表力:流体压强p 为法向外表应力,内摩擦τ是切向外表应力〔静止时为0〕。
2. 质量力〔体积力〕:*种力场对流体的作用力,不需要接触。
重力、电磁力、电场力、虚加的惯性力 3. 单位质量力:x y z Ff f i f j f k m==++,单位与加速度一样2m s 4. 流体静压强:1〕流体静压强的方向总是和作用面相垂直且指向该作用面,即沿着作用面的内法线方向2〕在静止流体内部任意点处的流体静压强在各个方向都是相等的。
第四章 扭转§4—1 工程实例、概念一、工程实例1、螺丝刀杆工作时受扭。
2、汽车方向盘的转动轴工作时受扭。
3、机器中的传动轴工作时受扭。
4、钻井中的钻杆工作时受扭。
二、扭转的概念受力特点:杆两端作用着大小相等方向相反的力偶,且作用面垂直杆的轴线。
变形特点:杆任意两截面绕轴线发生相对转动。
轴:主要发生扭转变形的杆。
§4—2 外力偶矩、扭矩一、外力:m (外力偶矩)1、已知:功率 P 千瓦(KW ),转速 n 转/分(r /min ; rpm)。
外力偶矩:m)(N 9549⋅=nPm 2、已知:功率 P 马力(Ps),转速 n 转/分(r /min ;rpm)。
外力偶矩:m)(N 7024⋅=nPm 二、内力:T (扭矩) 1、内力的大小:(截面法)mT m T mx==-=∑002、内力的符号规定:以变形为依据,按右手螺旋法则判断。
(右手的四指代表扭矩的旋转方向,大拇指代表其矢量方向,若其矢量方向背离所在截面则扭矩规定为正值,反之为负值。
)3、注意的问题:(1)、截开面上设正值的扭矩方向;(2)、在采用截面法之前不能将外力简化或平移。
4、内力图(扭矩图):表示构件各横截面扭矩沿轴线变化的图形。
作法:同轴力图:§4—3 薄壁圆筒的扭转 一、薄壁圆筒横截面上的应力(壁厚0101r t ≤,0r :为平均半径) 实验→变形规律→应力的分布规律→应力的计算公式。
1、实验:2、变形规律:圆周线——形状、大小、间距不变,各圆周线只是绕轴线转动了一个不同的角度。
纵向线——倾斜了同一个角度,小方格变成了平行四边形。
3、切应变(角应变、剪应变):直角角度的改变量。
4、定性分析横截面上的应力(1) 00=∴=σε ;(2)00≠∴≠τγ因为同一圆周上切应变相同,所以同一圆周上切应力大小相等。
⑶ 因为壁厚远小于直径,所以可以认为切应力沿壁厚均匀分布,而且方向垂直于其半径方向。
第4章 变形率和旋率有限变形:与t 有关,t 作为参变量。
——变形几何学 现在把时间考虑进去,研究变形的速度问题。
对时间求导数:两种描述法对时间求导数有区别,速度是求物质导数,固定K X ,对时间求偏导数——变形运动学。
§4.1 物质变形梯度的物质导数Lagrange 描述法:),(t X x x K k k =(物质)变形梯度张量:Grad kk KKx X ∂=⊗∂∂==∂F i I xF x X物质导数:()|KX t∂=∂F F (“K X |”表示保持K X 不变) 2(,)(Grad t t t t ∂∂=∂∂∂∂∂==∂∂∂∂∂==∂Xx X Xx x X X v v X§4.2 速度梯度张量变形梯度张量的物质导数∂∂∂===⋅∂∂∂v v x FG F X x X(1) 定义:∂=∂vG x称为速度梯度张量 grad =vl k kl v G ,=由(1),可得:1-=⋅G FF ,k l k l v =⊗G e e 速度梯度张量ⅢXⅠXⅡX1d X0=tG 比F用处更大。
§4.3 线元d x 的物质导数初始构形中的线元d X , 现时构形中的线元 d xd d =x F X求:d x 对时间的物质导数:(d )(d )d d x F X FX G F X ===⋅⋅ 则(d )d x G x =⋅ 反映了线元的变化速度。
空间线元的物质导数等于速度梯度与空间线元的点积。
§4.4 G 的加法分解F 用极分解,1-F 存在而G 用加法分解,1-G 不一定存在=+G D Ω 分解对称部分和反对称部分T 1()2=+D G G T 1()2=-ΩG G )(21,,k l l k kl v v D += )(21,,k l l k kl v v -=Ω变形率张量:D整旋率张量:Ω (物质旋率)(d )d d =+⋅x D x Ωx 1.变形率张量D 。
二阶对称张量,有三个相互垂直的主方向 (1,2,3)αα=n ,主值αD(a D α)α=⋅⊗D n n((d d d D x D x α)ααββα)αα⋅=⊗⋅=⋅D x n n n n由上式看出,D 为变形率张量,αD 为αn 方向变形速率,αn 为变形率标架。
2.旋率张量Ω,反对称张量,只有三个独立的分量*d d d ⋅==⨯Ωx x ωx 写为只要:321Ω=ω,132Ω=ω,21Ω=3ω,则上式成立。
ω称为轴矢量,转动角速度。
§4.5 变形速度张量Euler 描述法:222)d (d d )d ()d (L x x L l l k kl -=-δ求物质导数:l k kl l k kl l k kl x x x xx x tl t L l t d d d d )d d (d d)d (d d )d d (d d 222δδδ+===- ,d d k k K K x x X =,,,,,d d d d d k k K K k K K k l l K K k l lxx X v X v x X v x ====则 22,,T d(d d )()d d d 12d d (())22d d k l l k k l kl k l l L v v x x tD x x -=+==+=D G G xD x或写成 )(21,,k l l k v v +称为Euler 变形速度张量。
D (前面称为变形率张量),有了Euler 变形速度张量便可知)d d (d d 22L l t-。
线元l d 的伸长率:l k kl x x D l t l l t d d 2)d (d dd 2)d (d d 2=⋅= 除以2)d (2l ,则:l k kl l k kl n n D lx l x D l l t =⋅=d d d d d )d (d d(其中k n ,l n 分别为l d 在k 和l 方向的方向余弦)知道D 后,任何d x 的单位长度的变化率可用D 表示出来。
Lagrange 描述法:2T d(d )2d d d 2d d (d d )l t===xD xXF DF X x F X (*)∴Larange 变形速度张量为:T =⋅⋅EF D F 另推:Green 变形张量:C2222d d d d d d d (dl d )d d d d d KL K L KL K LKL K Ll L C X X X X L C X X t-=-δ-=⋅=⋅⋅X CX (**)比较(*)与(**)式,Green 变形张量的物质导数T 22==⋅⋅CE F D F §4.6 应变速度张量Lagrange 描述法: Green 应变张量:1()2=-E C I 求物质导数:T 12==⋅⋅EC FD FLagrange 应变速度张量:=Lagrange 变形速度张量。
另推:T TT 111()()222==⋅=+⋅EC F F F F F FT T T T T T 1()21()2=⋅⋅+⋅⋅=+=⋅⋅F G F F G F F G G FF D FEuler 描述法: Euler 型应变张量:11()2-=-e I B (Almansi 应变张量) (前面:1-B 称为Cauchy 变形张量)11T 1()()---=B F F求物质导数:1-T 1-T 111()[()()]22-⋅⋅--⋅=-=-+eB F F F F 1-=FF I ,则 110--+⋅=FFF F 则 11--=-⋅FF G 同样:TTT-=-⋅FG F则:T 111[]2--=+⋅eG B B G 又 12-=-+Be I则:TT 1()()2=+-+eG G G e eG T ()=-+D G e eGEuler 应变速度张量e 与Euler 变形速度张量不同。
即使0=D ,e也不一定为零。
若0=D (即线元长度不变化)则T=-=G G Ω(只有旋率张量)0≠e (应变仍存在)∴=⋅-⋅eΩe e Ω 不为零。
§4.7 各种旋率张量1. 主旋率张量T 1()2=-ΩG G ——物质旋率,,1()2kl kl k l l k v v Ω=-Ω=-grange 旋率张量设123,,e e e 固定在空间的标架——绝对标架eF 的极分解:=F QUF VQ =U 的主方向123M ,M ,M 也构成标架——Lagrange 标架,U 是变化的,则对应的Lagrange 标架也变化,该变化引起的旋转变化率称为Lagrange 旋率。
L =⋅M Q e (Q L 是一个正交张量,只是标架转动)T d ()d L L L t=⋅=⋅⋅M Q e Q Q M (T ()L =⋅e Q M ) T ()L L L =⋅ΩQQ 称为Lagrange 旋率张量。
可证LΩ是反对称张量L Q 是正交张量,即 T ()L L ⋅=Q Q I ∴L Ω是反对称张量。
3. Euler 旋率张量V 的三个主方向,123m m m 构成Euler 标架,m1x2x3x 1M2M3M3e2e1eT T T ()()0()0L L L L L L +=+=QQ Q Q ΩΩE =m Q i (E Q 正交张量)T d ()d E E E t==m Q e Q Q m T ()E E E =ΩQQ 称为Euler 旋率张量。
4. 伸长率标架旋率(变形率)变形率:D也有三个方向123n n n 构成一个标架nD =n Q eT d d d ()d D D D D tt===n Q e n Q e Q Q nT ()D D D =ΩQQ 称为伸长率标架旋率。
5. 相对旋率张量:R ΩEuler 标架相对于Lagrange 标架的转动速度。
M 表示Lagrange 标架,m 表示Euler 标架。
Q :表示从Lagrange 标架到Euler 标架的转动(与极分解Q 相同)m QM =求相对运动,视M 为不动的标架(实际上在动) ∴相对旋率:T R =⋅ΩQQ Q 为正交张量,R Ω为反对称张量。
§4.8 主旋率和相对旋率的关系T 1()2ΩG G =-——物质旋率T R ===ΩQQ();F QU VQ 相对旋率 F 的极分解:F QUFQU QU ==+又 FGF = 则 11G FF(QUQU )F --==+又 1T 11T UF U F Q Q ---===则 T 1T G QQQUU Q -=+ 1T R -=+ΩQUU Q 同理:T T 1T ()R -=+G ΩQU UQ∴ T 11T 1122R --=-=+-Ω(G G )ΩQ(UUU U )Q t :时间在动力学中确定与时间有关。
在静力学中,该时间概念有的所不同,认为荷载增量,应变增量,变形增量,——增量理论,就提出了有变形率、应变率问题,借用时间t 来考虑增量问题,其实不与时间紧密相关。