下载文档原格式
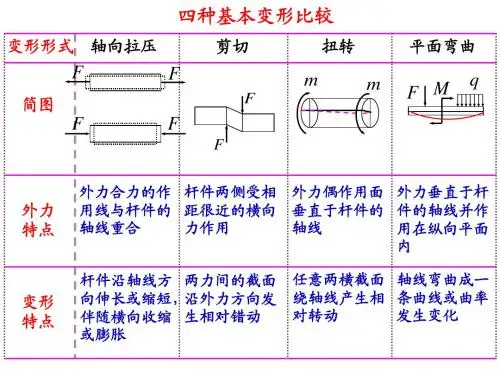
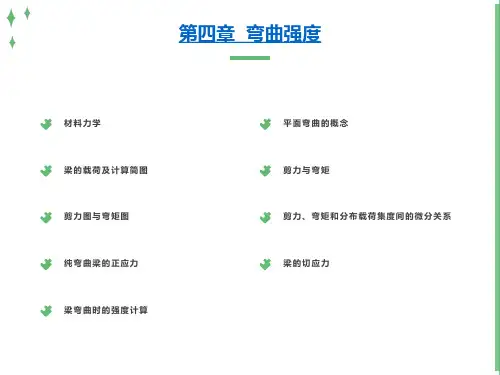
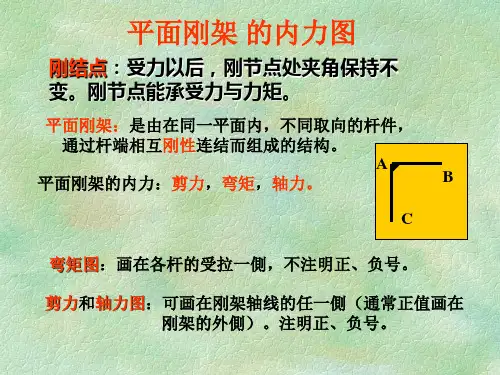
产生平面弯曲的充分条件和必要条件在数学和几何学中，平面弯曲是一个非常有趣且复杂的概念。
要了解产生平面弯曲的充分条件和必要条件，我们需要深入探讨这个主题，并从简单到复杂地逐步展开。
在本文中，我将逐步讨论平面弯曲的定义、充分条件和必要条件，并共享我对这个主题的个人观点和理解。
1. 平面弯曲的定义让我们回顾一下平面弯曲的定义。
在数学中，一个曲线或曲面称为“弯曲”，是指它在某一点的曲率不为零。
曲率是描述曲线“弯曲程度”的一个重要概念，它可以通过曲线的切线和曲率圆来进行定义。
要判断一个平面是否弯曲，我们就需要考察其曲率是否存在，以及曲率的大小和变化情况。
2. 充分条件我们来讨论产生平面弯曲的充分条件。
在几何学中，充分条件是指当一个条件成立时，结论一定成立。
对于平面弯曲来说，产生平面弯曲的充分条件包括但不限于：- 曲线或曲面存在非零曲率，即曲线或曲面在某一点的切线与曲率圆有交点。
- 曲线或曲面有较大的二阶导数，即曲线或曲面的变化率较大。
- 曲线或曲面有较大的弯曲程度，即曲线或曲面的弯曲程度不为零。
综合以上条件，我们可以得出产生平面弯曲的充分条件是曲线或曲面在某一点存在非零的曲率，并且有较大的弯曲程度和变化率。
3. 必要条件除了充分条件之外，我们还需要讨论产生平面弯曲的必要条件。
必要条件是指当结论成立时，某一条件一定成立。
对于平面弯曲来说，产生平面弯曲的必要条件是：- 曲线或曲面在某一点的曲率不为零。
- 曲线或曲面的切线存在曲率圆，即切线和曲率圆有交点。
- 曲线或曲面的曲率变化率不为零。
通过以上讨论，我们可以得出产生平面弯曲的必要条件是曲线或曲面在某一点存在非零的曲率，并且曲率有变化。
个人观点和理解从上面的讨论可以看出，产生平面弯曲的充分条件和必要条件在一定程度上是相互关联的。
在实际问题中，我们需要综合考虑这些条件，并运用适当的数学工具来进行分析和证明。
产生平面弯曲的条件还与空间的曲率和弯曲程度有密切关系，因此需要在实际问题中进行具体分析和推导。
