当前位置：文档之家 › 第四章弯曲挠度3-Lu

第四章弯曲挠度3-Lu

  • 格式：ppt
  • 大小：838.00 KB
  • 文档页数：48

下载文档原格式

  / 48

合集下载

挠度

挠度

挠度
科技名词定义
中文名称：挠度
英文名称：deflection
定义：结构构件的轴线或中面由于弯曲引起垂直于轴线或中面方向的线位移。

所属学科：水利科技（一级学科）；工程力学、工程结构、建筑材料（二级学科）；工程力学（水利）（三级学科）
本内容由全国科学技术名词审定委员会审定公布
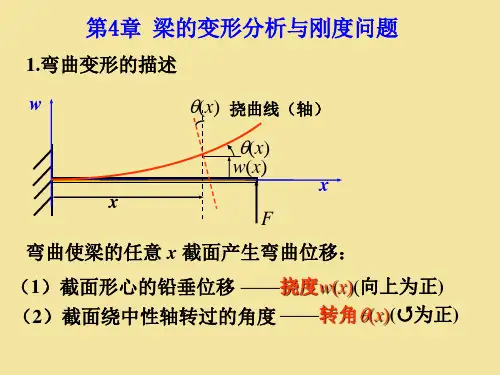
挠度（德语 Durchbiegung，法语la flèche）——弯曲变形时横截面形心沿与轴线垂直方向的线位移称为挠度，用y表示。

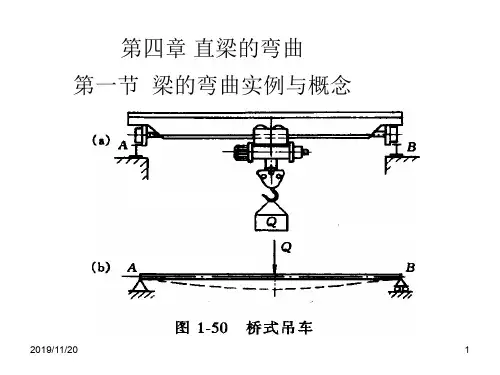
简言之就是指梁、桁架等受弯构件在荷载作用下的最大变形，通常指竖向方向y轴的,就是构件的竖向变形。

挠曲线——如图，平面弯曲时，梁的轴线将变为一条在梁的纵对称面内的平面曲线，该曲线称为梁的挠曲线。

挠度与荷载大小、构件截面尺寸以及构件的材料物理性能有关。

挠度——弯曲变形时横截面形心沿与轴线垂直方向的线位移称为挠度，用 y表示。

转角——弯曲变形时横截面相对其原来的位置转过的角度称为转角，用θ表示。

挠曲线方程——挠度和转角的值都是随截面位置而变的。

在讨论弯曲变形问题时，通常选取坐标轴x向右为正，坐标轴y向上为正。

选定坐标轴之后，梁各横截面处的挠度y将是横截面位置坐标x的函数，其表达式称为梁的挠曲线方程，即
y = f ( x ) 。

显然，挠曲线方程在截面x处的值，即等于该截面处的挠度。

根据微积分知识，挠曲线的斜率为
因工程实际中梁的转角θ之值十分微小，可近似认为
可见，挠曲线在截面位置坐标x处的斜率，或挠度y对坐标x的一阶导数，等于该截面的转角。

关于挠度和转角正负符号的规定：在如图6-1选定的坐标系中，向上的挠度为正，逆时针转向的转角为正。

化工机械设备基础 第四章 弯曲

化工机械设备基础 第四章 弯曲


0
RA 0.8 M 0 M RA 0.8 6.25 0.8 5kN
所得结果均为正，说明所 设的剪力和弯矩的方向（转 向）与实际相同。
第二节 剪力和弯矩
第二节 剪力和弯矩
结论： （1）梁任意横截面上的剪力，数值上等于该截 面一侧所有外力的代数和； （2）梁任意横截面上的弯矩，数值上的等于该 截面一侧所有外力对该截面形心力矩的代数和。
6求最大转角和最大挠度由图可见左右两支座处的转角的绝对值相等均为最大值分别以x0及xl代入上式可得最大转角为?最大挠度在梁距中点即xl2处其值为eiqlba243max?eiqlvvlx384542max?三用叠加法求解梁的变形当梁上同时作用几个载荷时可先求出各个载荷单独作用下梁的挠度和转角然后将它们代数相加即可得到几个载荷同时作用时梁的挠度和转角
i 1
第六节 强度计算
为保证梁的安全工作，必须保证其在许用应力 之内工作，其应力条件为：
M max max [ ] Wz
第六节 强度计算
三、静力学关系
从纯弯曲的梁中截开一 个横截面如图419所示。 在截面中取一截面积dA。 由于梁弯曲时x轴方向合 力为零，合力矩为M。
dA 0
A
ydA M
A

E

y

A
ydA yc A 0
静矩
第四节 纯弯曲时正应力
一、几何关系 二、物理关系

y


E
E

y
三、静力学关系
ydA M
A
第四节 纯弯曲时正应力
求解得应力计算式：

My
2
y dA
A
2 A
挠度

挠度


dw1 dx
1 0
得：
f中与 fmax相差
位移计算中的叠加原理
1.叠加原理（对线弹性材料，小变形）
由于内力 因此
是载荷
的线性函数。
同理，结构中的位移 （如 u,, w, ） 也是载荷
的线性函数，故也有
w wF wq wm
F q m
称为叠加原理
2.弯曲位移计算的载荷叠加法 利用基本变形表13.2
F

Fb h
l
解：曲梁压平产生弯曲变形，梁中产生弯曲应力。
压平后与刚平面接触——地面对梁有均布支持力q。
F
F 由平衡条件得：
ql 2F, q 2F
q
l
例题
例 题 13-12
F
Fb
ql 2F, q 2F
h
l

均布载荷简支梁
F
l
q
的弯曲挠曲线为：
F w qx (l3 2lx2 x3) 24EI
与w轴及m的符号规定有关挠曲线近似微分方程ei计算梁的位移的积分法挠曲线近似微分方程eidxeidxdwcxdxdxei其中cd为积分常数对分段的mx每段有2个常数若分n段有2n个常数
第4章 梁的变形分析与刚度问题
1.弯曲变形的描述
w
(x) 挠曲线（轴）
(x)
w(x) x
x F
弯曲使梁的任意 x 截面产生弯曲位移：
挠度连续 转角连续
w w i xxi
ቤተ መጻሕፍቲ ባይዱ
i1 xxi
i xxi
i1 xxi
仅挠度连续，转角不连续
A w1(x) w2(x) C lB l
B点挠度连续 w1 xl w2 xl
化工设备机械基础-弯曲扭矩

化工设备机械基础-弯曲扭矩



1 4
P

L

1 4

27.5
2.4

16.6kN.m
由型钢表查得16号工字钢的Wz=141cm3
max

M max WZ

16.5103 141106
117.86MPa 120MPa
2019/11/20
37
例3-6：选择工字钢型号。
P1
P2
已知：
P1 15kN , P2 21kN
a RA 4.83m q
M max

RA (a

2)

1 2
qa2

6.04kN
m
2019/11/20
27
第四节 弯曲时横截面上的正应力及其分布规律
一、纯弯曲的变形特征
2019/11/20
28
二、中性层的概念及性质:中性层 中性轴
mn
a
a
o
o
b
b
mn
变形前
x 中性轴
z y
现象：
① mm,nn 变 形 后 仍 为 直 线。
2019/11/20
剪力斜率：d
2M (x) dx2

dQ(x) dx

q(x)
23
若梁上无均布荷载，剪 力图为一平行于x轴水平 线。集中力偶作用处剪 力图无变化，弯矩图出 现突变，突变的绝对值 等于集中力偶的数值。
弯矩斜率：dM (x) Q(x) dx
2019/11/20
剪力斜率：d 2M (x) dx2

RA x2
P(x2
a)

Pb l x2
第四章(弯曲挠度3-Lu)

第四章(弯曲挠度3-Lu)

§4-9 用积分法计算梁旳挠度与转角
对于等截面梁，EI = 常数。
E I w "= - M (x)
EIw EI M ( x )dx C
EIw [ M (x)dx]dx Cx D
式中C, D 由梁支座处旳已知位移条件即位 移边界条件拟定。
HOHAI UNIVERSITY
EIw EI M ( x )dx C
C wc2(q)
c 2 (q)
HOHAI UNIVERSITY
3o 求 c、wc
A
c c (F ) c1(q) c2 (q)
F
C (F)
C (F )
B
C
qa 3 qa 3 qa 3
4 EI 6 EI 3EI
qa 3 4 EI
（b）
q
B
（d）
C
wc1(q) c1 (q )
wc wc (F ) wc1(q) wc2 (q)
EI 2
Fb 2l
x2
F 2
(
x
a
)2
C2
EIw2
Fb 6l
x3
F 6
(x
a)3
C2 x
D2
HOHAI UNIVERSITY
F
边界条件：x = 0 ，w1= 0。 x = l ，w2= 0。
a
b
A
CD
Bx
x
y
l
连续条件：x = a ，w1′= w2′， w1= w2
由连续条件，得：C1= C2， D1= D2
EIw [ M ( x)dx]dx Cx D
如：
p
A
B
p A
边界条件： wA=0 wB=0
边界条件： wA=0 θA=0
材料力学第4章-弯曲强度1

材料力学第4章-弯曲强度1


T

T

切应变
γ
φ r0 l
扭 转/薄壁圆轴的扭转
扭转回顾
剪切胡克定律
G
G——材料的剪切弹性模量


dy
dz
dx

切应力互等定理：二个相互垂直的截面上，垂直于两截 面交线的切应力大小相等，方向均指向或离开该交线。
扭 转/圆轴扭转时的应力和变形
扭转回顾
圆轴扭转时
横截面上切应力
FS FAy F1
剪力与弯矩
三、实用法则
左顺右逆，M为正。
弯矩：考虑横截面左侧梁段时，顺（逆）针旋转的外力
矩产生 +（-）弯矩，（右侧相反）， 代数和结果为 + (-)时，弯矩为 + (-) 注：对任一侧梁段，向上（下）的外力产生 +（-）弯矩
a F1
M M
F2
b
x FAy
FQ
FS
F FQ S
例 1 试求图示外伸梁A、D左与右邻截面上的FS和M。 qa qa q 解：2.求内力
2
D左邻截面：
FSD左 qa 1 4
a 2 )
C
A a a 1
4
D a
qa
B a 7
4
E
qa
3 4 1
4
qa
qa a
C
FAy
q A a FAy
FBy
qa
M D左 qa (a 5 4 qa
剪力图和弯矩图
三、列方程法作剪力图和弯矩图
例 2 作图示梁的内力图。 解： 1.求支反力 2.列内力方程
FS x ql 2 qx
q A
材料力学课件4第四章弯曲内力4-3(附录I)

材料力学课件4第四章弯曲内力4-3(附录I)


h
O
x
b
dA=b· dy
y dy y
O
h
x
b
bh I x = y dA= y bdy A h / 2 12
2 h/2 2
3
( 公式熟练掌握：宽×高3/12） 同理：
hb I y = x dA= x hdy A b / 2 12
2 b/2 2
3
例I-4：计算如图的惯性矩Ix , Iy,。 y d
将有关尺寸(mm)标在图中 y' C2
250
C1
O'
x
98 .3 26 .7
C3
26 .7
19 .21
y 0
A 24.1mm A x 4491(19.21 26.7) 2 2030 0 x
i i
.
4491 2 2030
将有关尺寸标在图中，标形心轴x-y轴 y y' 24 .1
Sx A
组合图形计算形心坐标的公式(I—2a)为：
x
A
xdA A

Sy A
S A
y ,i
Ax A
i i
y
A
ydA A
Sx Sx ,i A i yi A A A
(I—4)
形心坐标的公式(I—2a) 可改写为：
Sy Ax
常用，掌握
Sx Ay
(2) 由
Sx Ay
Sy Ax
2
y
bh h bh Sx Ay 2 3 6
h
C
b
h/3 x
补例：计算如图(a)的静矩Sz ,Sy, 图(b) Sz 。
材料力学 第4章 弯曲强度-3

材料力学 第4章 弯曲强度-3


z
z
h h/b = 2 wz=0.236
D
wz=0.141
b
h/b = 10 wz=0.527
材料
第四章 弯曲强度：梁的合理强度设计
力学
采用变截面梁
设计目标： 使梁所有横截面的最大正应力等于许用应力 —— 等强度梁
悬臂梁等强度设计
材料
第四章 弯曲强度：梁的合理强度设计
力学
实用近似等强度梁
✓ 确定FP加在辅助梁的什么位置
材料
第四章 弯曲强度：梁弯曲时的强度计算
力学
✓ 确定FP的位置 令： 解出 ： 得到 ：
材料
第四章 弯曲强度：梁弯曲时的强度计算
力学
✓ 确定辅助梁所需要的 工字钢型号
因此，Mmax=M (x=2.667 m)
材料
第四章 弯曲强度：梁弯曲时的强度计算
力学
✓ 确定辅助梁所需要的 工字钢型号
由强度条件
max

M max Wz
[ ]
由此，可以算出辅助梁所需要的弯曲截面模量：
Wz

M max (B)
[ ]

300kN 103 160MPa 106
1.875103 cm3
材料
第四章 弯曲强度：梁弯曲时的强度计算
力学
✓ 确定辅助梁所需要的工字 钢型号
由工字钢型钢表中查得 50a工字钢 Wz = 1.860×103 cm3 50b工字钢 Wz =1.940×103 cm3
(10×106)×(139) 403×105
(10×106)×(-61) 403×105
= 30.3 MPa = -69.0 MPa = 34.5 MPa = -15.2 MPa
化工设备机械基础第四章 弯曲

化工设备机械基础第四章 弯曲


IZ WZ ymax
bh bh 2 12 h 6 2
28
2.圆形及圆环形截面的惯性矩和抗弯截面模量
D
z
Iz

64
D ,
4
Wz

32
D ,
3
D d z
Iz

64
(D d )
4 4

64
D 4 (1 4 )
d ( ) D
Wz

32
D (1 )
3 4
A 2、截取m-m截面左段。 B
x
m
L
RA
A
RB
剪力 Fs ——使截面不产生移动 弯矩M ——使截面不产生转动 由 Y 0, 得到：
由 M o 0,
m
M
Pb Fs RA L
RA
x
Fs
m
得到：
1
Pb M RA x x L
m
A
o
M
3、截取m-m截面右段梁: 由作用力与反作用力，得
载荷
q ( x) 0
q C 0 q C 0
F
Mo
水平直线
Fs 图 + or 上斜直线 下斜直线
斜直线
F
(剪力图 无突变)
M 图
or
下凸 抛物线
上凸 抛物线
F处有尖角
Mo
26
My Iz
M——横截面上的弯矩 y ——所求点到中性轴的距离 IZ ——横截面对中性轴Z的惯性距

M
横截面上的正应力分布 横截面上最大正应力为
q B x 2a
RB
x
a
A
弯曲4-5、6、7

弯曲4-5、6、7


F压机 ≥ 1.2 ~ 1.3（F自 + FY） ( )
对于校正弯曲 对于校正弯曲 校正
F压机 ≥ 1.2 ~ 1.3) F校 (
第四章 弯曲
第六节 弯曲件的工艺性
第六节 弯曲件的工艺性
定义: 指弯曲件结构形状、尺寸精度要求、 定义: 指弯曲件结构形状、尺寸精度要求、 材料选用及技术要求是否适合于弯曲加工 的工艺要求。 的工艺要求。 一、弯曲件的精度 一般弯曲件的经济公差等级在IT13级以下， 一般弯曲件的经济公差等级在IT13级以下， 公差等级 级以下 角度公差大于15´ 大于15 角度公差大于15´。 二、弯曲件的材料 弯曲件的材料 三、弯曲件的结构工艺性
rmin / t 大，回弹
第四章 弯曲
三、弯曲件的结构工艺性 1.弯曲件的弯曲半径 1.弯曲件的弯曲半径 弯曲件的 2.弯曲件的形状 2.弯曲件的形状 弯曲件的 3.弯曲件直边高度 3.弯曲件直边高度 弯曲件 4.弯曲件上孔的位置 4.弯曲件上孔的位置 弯曲件上 5.弯曲件上增添工艺孔和工艺槽 5.弯曲件上增添工艺孔和 弯曲件上增添工艺孔 6.定位工艺孔 6.定位工艺孔
第四章 弯曲
第五节 弯曲力的计算
二、校正弯曲时弯曲力计算
F = qA
F——校正弯曲应力； 校正弯曲应力； 校正弯曲应力 A——校正部分投影面积； 校正部分投影面积； 校正部分投影面积 q——单位面积校正力，其值见下表。 单位面积校正力， 单位面积校正力 其值见下表。
第四章 弯曲
第五节 弯曲力的计算
第六节 弯曲件的工艺性
5.弯曲件上增添工艺孔和工艺槽 5.弯曲件上增添工艺孔和工艺槽 为了防止在尺寸突变的尖角处出现撕裂， 为了防止在尺寸突变的尖角处出现撕裂，应 尺寸突变的尖角处出现撕裂 使突变处离开弯曲线，或在尺寸突变处预冲工 离开弯曲线 使突变处离开弯曲线，或在尺寸突变处预冲工 艺槽、工艺孔。 艺槽、工艺孔。
15第十五讲(弯曲位移和积分法)

15第十五讲(弯曲位移和积分法)


b x2 F C1 EIw1 l 2 b x EIw C1 x D1 1 F l 6
3
b x 2 F x a F EIw2 C2 l 2 2
2
b x 3 F x a EIw2 F C2 x l 6 6 D2
横力弯曲时，尽管剪切变形对梁的变形也会产生影响，但 在一般工程中影响较小（长高比较大），因此
1
1 M x x x EI
三峡大学 工程力学系
材料力学教案
第十五讲：弯曲位移及积分法
几何方面，平面曲线的曲率可写作
1 w x 1 w2


3/ 2

三峡大学 工程力学系
材料力学教案
第十五讲：弯曲位移及积分法
例题 试求图示等直梁的挠曲线方程和转角方程，并确定
其最大挠度wmax和最大转角qmax。
三峡大学 工程力学系
材料力学教案
第十五讲：弯曲位移及积分法
解：该梁的弯矩方程为
M x ql 1 q x qx 2 lx x 2 2 2 2
三峡大学 工程力学系
材料力学教案
第十五讲：弯曲位移及积分法
两段梁的挠曲线近似微分方程亦需分段列出，并分别进行积分： 左段梁 0 x a
右段梁 a x l
挠曲线近似微分方程
b M 1 x F x EI w1 l 积分得 b M 2 x F x F x a EI w2 l
材料力学教案 第四章我们学到
第十五讲：弯曲位移及积分法
（1）弯曲变形的应力计算及其强度问题。
三峡大学 工程力学系
材料力学教案
第十五讲：弯曲位移及积分法

4弯曲强度解析

q(x) dx
dx
M Fs
O
M dM
Fs dFs
q(x)
Fy 0 ：FS (x) FS (x) dFS (x) q(x) • dx 0
dFS (x) q(x)
dx
MO
0 ：M (x) dM (x)
M (x)
FS (x) • dx
1 2
q(x) • dx2
0
dM (x)
dx 《材料力学》 刘加一
M 0 : M 《材料力学C》 刘加一 F（B l x) F a x 0 M F（B l x) F a x FA9x
§4-2 平面弯曲梁的内力
①剪力：平行于横截面的内力
符号规定：凡使梁段产生顺时针方向转动趋势的剪力为正，
反之为负
FS
FS
FS
FS
剪力为正
剪力为负
②弯矩：绕截面转动的内力
《材料力学》 刘加一
24
§4-2 平面弯曲梁的内力
例4-2-6
3kN
外伸梁AB承受6kN荷载m 如图所示，作该梁的FS—M图。
2kN /m
解： 1、求支反力
A C
B D
FA 7.2kN FB 3.8kN
1m
4m
FA
FS
4.2 (kN)
+
E
_
3
x=3.1m
1m
FB
_
3.8
2、判断各段FS、M图形状： CA和DB段：q=0，FS图为水 平线，M图为斜直线。 AD段：q<0， FS 图为向下斜 直线， M图为上凸抛物线。
剪力、弯矩方程：
MFS
(x) (x)
F F
x
Fx A

第四篇(弯曲挠度3Lu)


2EI
B
a
C
B
F
B
C
M=Fa
HOHAI UNIVERSITY
A1
Fa 2 2EI
,
A1
Fa 3 3EI
F
A wA1 θA1
A2
B
Fa 2 4EI
A wB
A2
B
Ba
Fa 3 6EI
Fa 3 4EI
5Fa3 12 EI
B a
A3
B
Fa 2 2EI
A
A2
B
Ba
Fa 3 4EI
Fa 3 2EI
ql 3 6 EI
ql 4 wc1(q) 8EI
2 AB变形，BC不变形（刚化）。
c 2 (q)
B (q)
ml 3EI
1 2
qa
2
2a
qa3
A
3 EI
3EI
wc2(q) B (q) a
qa4
3EI
q
B
（c）
q
B
（d）
C
C
wc1(q) c1 (q )
qa2/2
B
（e）
C wc2(q)
c 2 (q)
HOHAI UNIVERSITY
3o 求 c、wc
A
c c (F ) c1(q) c2 (q)
F
C (F)
C (F )
B
C
qa3 qa3 qa3 4EI 6 EI 3EI
qa3 4 EI
（b）
q
B
（d）
C
wc1(q) c1 (q )
wc wc (F ) wc1(q) wc2 (q)
HOHAI UNIVERSITY

材料力学附录挠度表

材料力学附录挠度表
在材料力学中，挠度表是用来计算物体的弯曲变形程度的参考表格。

挠度是指物体在受力作用下发生的弯曲变形的程度，也可以理解为物体在外力作用下的弯曲程度。

挠度表通常列出了不同形状和材料的物体在不同受力情况下的挠度计算公式或系数。

以下是一个简化的挠度表示例：
1. 材料：钢
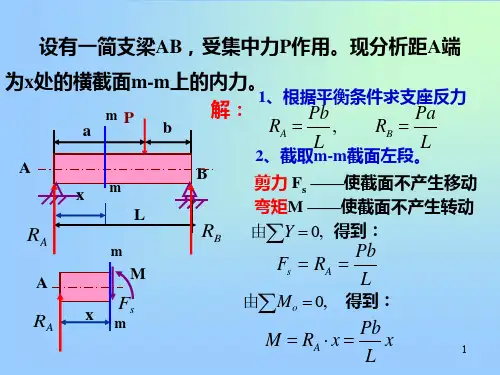
- 悬臂梁的挠度公式：δ = (WL^3) / (3EI)
- 支承梁的挠度公式：δ = (5WL^4) / (384EI)
其中，δ为挠度，W为受力点的载荷，L为梁的长度，E为弹性模量，I为截面惯性矩。

2. 材料：木材
- 悬臂梁的挠度公式：δ = (WL^3) / (48EI)
- 支承梁的挠度公式：δ = (7.5WL^4) / (384EI)
其中，δ为挠度，W为受力点的载荷，L为梁的长度，E为弹性模量，I为截面惯性矩。

3. 材料：铝合金
- 悬臂梁的挠度公式：δ = (WL^4) / (8EI)
- 支承梁的挠度公式：δ = (W*L^3) / (48EI)
其中，δ为挠度，W为受力点的载荷，L为梁的长度，E为弹性模量，I为截面惯性矩。

需要注意的是，挠度表中给出的公式或系数只是近似计算的结果，实际情况会受到许多其他因素的影响，如材料的非线性、梁的支撑方式等。

因此，在实际应用中，可能需要考虑更复杂的挠度计算方法或使用专业的材料力学软件进行分析。

10第四章弯 曲


冲压工艺及冲模设计—王志刚
第四章 弯 曲
20
第二节 最小弯曲半径 第 四 章 弯 曲
冲压工艺及冲模设计—王志刚
第四章 弯 曲
21
第二节 最小弯曲半径 第 四 章 弯 曲
二、影响最小弯曲半径的因素
1、材料的力学性能 材料的塑性愈好，许可的相对弯曲半径愈小。 2、弯曲中心角 α 的大小
理论上： 弯曲变形区局限于圆角区域，
冲压工艺及冲模设计—王志刚
第四章 弯 曲
17
第一节 弯曲变形过程及变形特点 第 四 章 弯 曲
小结：
弯曲概述： 第一节 弯曲变形过程及变形特点
一、弯曲变形过程
1、弯曲变形时板材变形区受力情况 2、弯曲变形过程
二、弯曲变形的特点
1、弯曲圆角部分是弯曲变形的主要区域 2、弯曲变形区内存在中性层 3、变形区材料厚度变薄和增长的现象 4、变形区板料剖面的畸变、翘曲、起皱和破裂 5、弯曲变形区中性层内移
冲压工艺及冲模设计—王志刚
第四章 弯 曲
9
第一节 弯曲变形过程及变形特点 第 四 章 弯 曲
2.弯曲变形过程
弹性弯曲变形： 弯曲圆角半径r很大， 弯曲力矩很小 弹-塑性弯曲变形： 内外表面 力臂L
塑性变形
毛坯内部 弯曲力矩
弯曲力 塑性弯曲变形： 板料截面全部进入塑性变形状态 贴模：板料与凸 、凹模完全贴紧
直边部分不参与变形，似乎变形 程度只与相对弯曲半径 r / t 有关， 而与弯曲中心角无关。 由于材料的相互牵制作用，接近圆角的直边也参与了变 实际上： 形，扩大了弯曲变形区的范围，分散了集中在圆角部分的弯 曲应变，使圆角外表面受拉状态有所缓解，从而有利于降低 最小弯曲半径的数值。
α

150508第十三讲：弯曲挠度

w x F
A
max
x
B w max
l
解：建立坐标系如图
x处弯矩方程为： M ( x) F (l x)
转角和挠曲线方程分别为：
列挠度微分方程并积分两次： EI " M ( x) F ( x l ) Fx 2 EI ' Flx C1 2 Fx3 Flx 2 EI C1 x C2 6 2
l/2
q
q
l/2
B 8 EI Ⅱ： l 3 q 2 C 2 B 6 EI
l l q 2 7 ql 4 C 2 B l B 8EI 2 6 EI 384 EI 4 3 l q 2
A
B
l/2
2. 挠度和转角的近似微分方程
dx
x
A
F x ω
B

y
ds

B1
d
d
1）力学关系： 2）几何关系：
1
M EI

1

1

2 32

平面曲线的曲率
M ( x) M ( x) EI EI
(1)自然（重力）坐标
x x
M ( x) EI
'
F ( x 2 2lx) 2 EI
F ( x 3 3lx 2 ) 6 EI
由边界条件决定积分常数：
' |x 0 0 ，得：C1 0； |x 0 0 ，得：C2 0
FL2 x l时， max B 2 EI 3 FL x l时， max B 3EI
q
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

( x a )2
w2
Fb( l 2 b2 )
Fb
x
6 EIl
6 EIl
x3 F 6 EI
( x a )3
当a b时，wmax应在AD段。
F
a
b
由w1 0，x0
l2 b2 。 3
A
x
y
CD l
Bx
wmax
w1
x x0
Fb（l 2
b
） 2
3 2
。
9 3EIl
wc
w1
x
l 2
Fb（3l 2 4b2）。 48EI
1
w
<<1
( x )
1 w2
3 2
1 M(x)
( x) EI z
A y
w M x
EI z
θ
p
C
w
p
C
θ
B x
HOHAI UNIVERSITY
O
x
O
x
M
M
y
M<0
w" > 0
M
M
y
M>0
w"< 0
w M x
EI z
w M x
EI z
—— 挠曲线近似微分方程
HOHAI UNIVERSITY
0.0625 Fbl 2 。 EI
a
b
A
CD
Bx
x
y
l
因此，受任意荷载的简支梁，只要挠曲线上没有 拐点，均可近似地将梁中点的挠度作为最大挠度。
HOHAI UNIVERSITY
总结：
➢挠曲线的微分方程：E I w "= - M (x)
➢数学求解： EIw EI M( x)dx C
EIw1
Fb l
x
HOHAI UNIVERSITY
EIw1
Fb l
x
F
a
b
EI w 1
EI 1
Fb 2l
x2
C1
A
CD
Bx
x
EIw 1
Fb 6l
x3
C1x
D1
y
l
Fb DB : M ( x ) x F ( x a )
l
EI w 2
Fb l
x
F(
x
a
)
EIw2
EI 2
Fb 2l
x2
F 2
(
HOHAI UNIVERSITY
当F作 用 于 梁 中 点C时 ，wmax wc。
当F右 移 至B点 时 ，b 0，x0 0.577l。
wmax的 位 置 距 梁 中 点 仅 0.077l。
令
b2 0,
wmax
Fbl 2 9 3 EI
0.0642 Fbl 2 。 EI
F
wc
Fbl 2 16 EI
HOHAI UNIVERSITY
第四章 弯曲变形
—— 梁的挠度计算
HOHAI UNIVERSITY
§4-7 梁的变形
θ
p
A
C
w
p
B x
C
θ
y
在平面弯曲情况下，梁的轴线在形心主惯性平
面内弯成一条平面曲线。此曲线称为梁的挠曲线。
当材料在弹性范围时，挠曲线也称为弹性曲线。
HOHAI UNIVERSITY
§4-9 用积分法计算梁的挠度与转角
对于等截面梁，EI = 常数。
E I w "= - M (x)
EIw EI M( x )dx C
EIw [ M (x)dx]dx Cx D
式中C, D 由梁支座处的已知位移条件即位 移边界条件确定。
HOHAI UNIVERSITY
EIw EI M( x )dx C
θ
p
A
C
w
p
B x
y
C
θ
1、挠度: 梁的截面形心在垂直于轴线方向的线位
移w。
w= w(x)——挠曲线方程(挠度方程)。向下为正.
2、转角：梁的截面绕中性轴转过的角度θ。
小变形时，θ≈tanθ=dw (x)/dx=w'(x)——转角方 程。顺时针为正。
HOHAI UNIVERSITY
§4-8 梁的挠曲线近似微分方程
EIw [ M(x)dx]dx Cx D
如：
p
A
B
p A
边界条件： wA=0 wB=0
边界条件： wA=0 θA=0
HOHAI UNIVERSITY
例1：一悬臂梁在自由端受集中力作用，求梁的 转角方程和挠度方程。并求最大转角和最大挠度。
设梁的抗弯刚度为EI。
F
A
B
l
HOHAI UNIVERSITY
x a )2
C2
EIw 2
Fb 6l
x3
F 6
(x
a)3
C2 x
D2
HOHAI UNIVERSITY
F
边界条件：x = 0 ，w1= 0。 x = l ，w2= 0。
a
b
A
CD
Bx
x
y
l
连续条件：x = a ，w1′= w2′， w1= w2
由连续条件，得：C1= C2， D1= D2
再由边界条件，得：C1= C2= Fb（l2-b2）/ 6l
EI 2EI
A
Flx 2 Fx 3
w
y
2EI 6 EI
F
Bx
θmax
wmax
l
当 x = l 时：
max
w
xl
ห้องสมุดไป่ตู้
Fl 2 2 EI
Fl 3 wmax w xl 3EI
HOHAI UNIVERSITY
例2：一简支梁受均布荷载作用，求梁的转角方程 和挠度方程，并确定最大挠度和A、B截面的转角。 设梁的抗弯刚度为EI。
q
A
B
l
HOHAI UNIVERSITY
解:1°建立坐标系。求支座反力。列弯矩方程：
FAy
FBy
1 2
ql
A
M ( x) ql x qx2
q l
Bx
2
2y
2o 梁的挠曲线微分方程为
EIw ql x qx2
2
2
积分 EIw ql x2 qx3 C 2 2 23
ql x3
qx4
EIw
Cx D
2 23 234
HOHAI UNIVERSITY
边界条件
x0: w0 xl: w0
q
A
θA
y
wmax θB
Bx
l
得:C ql 3 24 , D 0
w
ql 3
ql
x2
q
x3
24EI 4EI 6 EI
ql 3
ql
w
x
x3
q
x4
24EI 12EI 24EI
5ql 4
wmax
w
D1=D2=0 因此，梁各段的转角方程和挠度方程为：
AD :
w1
1
Fb( l 2 b2 6 EI
)
Fbx 2 2 EIl
w1
Fb( l 2 b2 ) x Fb
6 EIl
6 EIl
x3
HOHAI UNIVERSITY
DB :
w2
2
Fb( l 2 b2 ) 6 EIl
Fb 2 EIl
x2
F 2 EI
解：
A
1o M( x ) F( l x )
l
2o EIw M ( x ) y
Fl Fx
积分：
EIw' EI Flx Fx2 2 C
EIw Flx2 Fx3 Cx D 2 23
边界条件:
x 0:
w 0 w0
C0
D0
F Bx
HOHAI UNIVERSITY
w Flx Fx 2
x
l 2
384EI
A
x0
ql 3 24EI
B
xl
ql3 24EI
HOHAI UNIVERSITY
例3：已知F、EI，求梁的转角方程和挠度方程
及wmax 。
A
解:1°建立坐标系。
F
a
b
CD
Bx
求支座反力。
x
y
l
FAy
Fb l
,
FBy
Fa l
2°分段求出弯矩方程及w′、w。
AD :
M ( x ) Fbx , l