20.5 等腰梯形的判定(含答案)
- 格式:doc
- 大小:420.50 KB
- 文档页数:9
亳州十二中学教学案主备人:张振贵合备人:丁传宇张启文陈洪刚日期:46姓名班级学科数学教学内容16.3等腰梯形的判定教材分析等腰梯形的判定定理是由两个操作引入,教学时可以类比平行四边形的教学展开,在学生直观感知的基础上,再进行严格的推理证明,应该让学生依照定理的证明在当堂完成学情分析学生学习了等腰梯形的概念,以及等腰梯形的性质,在此基础上,学习等腰梯形的判定,从性质引入判定,学生更容易接受。
检测预习导学效果(要点)1、等腰梯形的判定方法有哪些?2、如何证明等腰梯形的判定方法?教学过程教学目标教师活动学生活动反思一、温故知新[活动1] 1.什么样的四边形叫梯形?什么样的梯形是直角梯形、等腰梯形?2.等腰梯形有哪些性质?[活动1]回顾等腰梯形的性质,并回答老师的提问。
试验探究,发现猜想:经历操作、发现、猜想,培养学生自主发现问题和合作交流的能力[活动2]1、我们已经掌握了等腰梯形的性质,那么又如何来判定一个梯形是等腰梯形呢?今天我们就共同来研究这个问题。
2、在同一底边上的两个内角相等的梯形是等腰梯形。
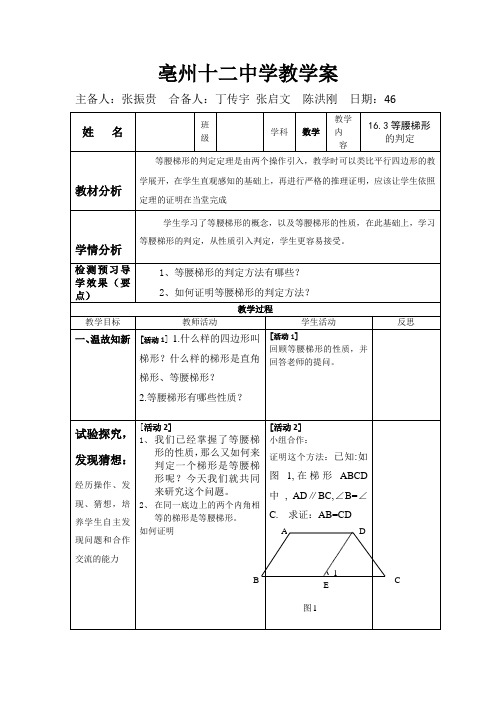
如何证明[活动2]小组合作:证明这个方法:已知:如图1,在梯形ABCD中, AD∥BC,∠B=∠C. 求证:AB=CD[活动3][活动3]AB CD图1E1合作交流,证明猜想:培养学生的逻辑思维能力;对角线相等的梯形是等腰梯形如何证明这个方法,请同学们小组合作探究已知:如图4梯形ABCD中,AD∥BC,对角线AC=BD.求证:梯形ABCD是等腰梯形.。
巩固练习,强化新知1.在四边形ABCD 中,∠A:∠B:∠C:∠D =2:4:4:2,则四边形ABCD是()A.任意四边形B.平行四边形C.直角梯形D.等腰梯形3.下列命题是假命题的是()A.等腰梯形的两条对角线相等B.对角线相等的四边形是等腰梯形C.等腰梯形是轴对称图形D.在同一底上的两个角相等的梯形是等腰梯形4.如图,在梯形ABCD中,AD∥BC, ∠ABC=60°,BD 平分∠ABC, BC=2AB.求证:四边形ABCD是等腰梯形。


等腰梯形的性质和判定适用精选文件资料分享等腰梯形的性质和判断§1.4 等腰梯形的性质和判断一、预习导学 1 、______________ _________________的图形叫做等腰梯形。
2 、____________相等的____________ ___叫做等腰梯形 ; 3 、依据等腰梯形的定义,一个图形要成为等腰梯形 , 第一它一定是 _____, 还要具备 _____相等 ; 4 、由等腰三角形的判判定理猜想等腰梯形的判断定理:定理的证明:已知:求证:(解析:本题可以从以下的三个角度着手证明(附三种方法的图形)。
)证法一:证法二:证法三:5、定理的书写格式∵∴_________________________ 6、等腰梯形的性质 1 、定理 1、等腰梯形同一底上的两底角相等。
定理 2 、等腰梯形的两条对角线相等。
2 、证明等腰梯形的性质二、自主研究如图,已知在梯形 ABCD中, AD∥BC,AB=DC,对角线AC和 BD订交于点 O,E 是 B C边上的一个动点(点E 不于 B、C 两点重合),EF∥BD交 AC于点 F。
EG∥AC交 BD于点 G。
(1)、求证:四边形 EFOG的周长等于 2OB;(2)、请将上述题目的条件“梯形A BCD 中, AD∥B C,AB=DC”改为另一种四边形,其余条件不变,使得结论“四边形EFOG的周长等于2OB”仍成立,并将改编后的题目画出图形,写出已知、求证,不用证明。
三、反响练习1、如图,等腰梯形 ABCD中, AD∥BC,AB=CD。
点 E 是 AD延长线上一点,DE=B C.(1)求证:∠ E=∠ DBC;(2)判断△ ACE的形状(不需要说明原由).2.如图2,在梯形ABCD中,AD∥BC,点 E 是BC边的中点,EM⊥AB,EN⊥CD,垂足分别为M、N且EM=EN.求证:梯形ABCD 是等腰梯形。
3.证明等腰梯形一底边的中点到另一底两端的距离相等。


等腰梯形的性质定理和判定定理及其证明西麓中学吴九成教学目标:知识目标:理解和掌握等腰梯形的性质定理的内容及简单的应用;能力目标:通过动手操作,探索等腰梯形的性质及其证明方法,初步培养学生探索问题和研究问题的能力;情感目标:营造一个相互协作的课堂气氛,引领学生自主探究、集体讨论,激发学生的学习热情;教学重点与难点:1、等腰梯形性质的探究及证明;2、等腰梯形性质定理的简单应用。
教学过程:1、复习旧知,引入新课填空(1)的四边形是平行四边形;(2)的四边形是平行四边形;(3)的四边形是平行四边形;(4)的四边形是平行四边形;(5)的四边形是平行四边形;(6)一组对边平行,一组对边相等的四边形是平行四边形;用举反例的方法举出有一组对边平行,一组对边相等但并不是平行四边形的图形即等腰梯形,从而由这个错误的判定引出梯形、等腰梯形、直角梯形的定义;我们这节课就来研究等腰梯形的性质。
2、自主探索、提出猜想把学生分成以四个人一组的若干小组,提供给每个小组一个等腰梯形的模型,让同学们用各种数学工具通过各种数学方法,如翻折、旋转等来探索等腰梯形有哪些性质?同学们可能会得出下面一些结论:(1)两腰相等;(2)两个底角相等;(3)等腰梯形是轴对称图形,不是中心对称图形;(4)两条对角线相等;…………结论(1)由等腰梯形的定义可以得到而不用证明;结论(2)的证明探索:的两种思路:)一是把两个角转化到同一个三角形中,用“等边对等角C二是把两个角转化到两个全等三角形中,用“全等三角形的对应角相等”证明;完善结论后得到:等腰梯形的性质定理 等腰梯形的同一条底边上的两个内角相等。
结论(3):观察翻折、旋转的动画演示后,由轴对称图形和中心对称图形的定义可以直接得到:等腰梯形是轴对称图形,经过两底中点的直线是它的对称轴。
等腰梯形不是中心对称图形!结论(4)的证明可以让学生独立完成,请一个同学上黑板板书,其他同学自己在课堂练习本上完成。
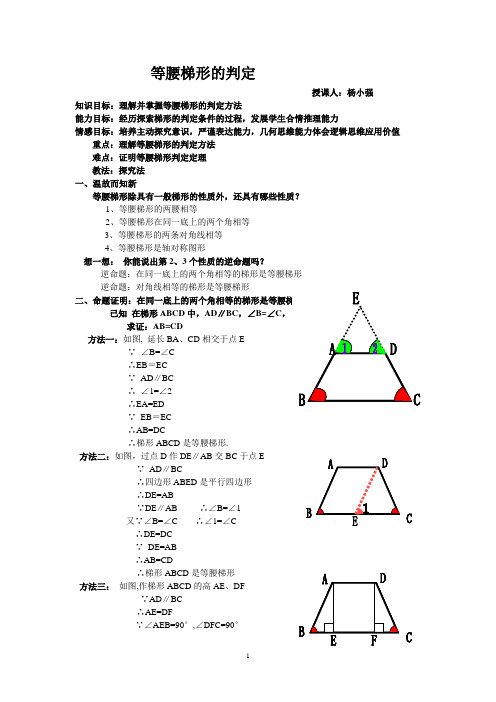
等腰梯形的判定授课人:杨小强知识目标:理解并掌握等腰梯形的判定方法能力目标:经历探索梯形的判定条件的过程,发展学生合情推理能力情感目标:培养主动探究意识,严谨表达能力,几何思维能力体会逻辑思维应用价值 重点:理解等腰梯形的判定方法 难点:证明等腰梯形判定定理 教法:探究法 一、温故而知新等腰梯形除具有一般梯形的性质外,还具有哪些性质? 1、等腰梯形的两腰相等2、等腰梯形在同一底上的两个角相等3、等腰梯形的两条对角线相等4、等腰梯形是轴对称图形想一想: 你能说出第2、3个性质的逆命题吗?逆命题:在同一底上的两个角相等的梯形是等腰梯形 逆命题:对角线相等的梯形是等腰梯形已知 在梯形ABCD 中,AD ∥BC ,∠B=∠C 求证:AB=CD方法一:如图, 延长BA 、CD 相交于点E ∵ ∠B=∠C∴EB =EC ∵ AD ∥BC ∴ ∠1=∠2 ∴EA=ED∵ EB =EC ∴AB=DC∴梯形ABCD 是等腰梯形.方法二:如图,过点D 作DE ∥AB 交BC 于点E ∵ AD ∥BC∴四边形ABED 是平行四边形 ∴DE=AB∵DE ∥AB ∴∠B=∠1又∵∠B=∠C ∴∠1=∠C∴DE=DC ∵ DE=AB ∴AB=CD∴梯形ABCD 是等腰梯形方法三: 如图,作梯形ABCD 的高AE 、DF ∵AD ∥BC ∴AE=DF∵∠AEB=90°,∠DFC=90°∴∠AEB=∠DFC∵∠B=∠C∴Rt △ABE ≌Rt △DCF(AAS) ∴AB=DC∴梯形ABCD 是等腰梯形.三、归 纳等腰梯形判定定理:在同一底上的两个角相等的梯形是等腰梯形 符号语言:如图 在梯形ABCD 中 ∵∠B =∠C ∴梯形ABCD 为等腰梯形 或者如图 在梯形ABCD 中 ∵∠BAD =∠CDA∴梯形ABCD 为等腰梯形 四、知识应用例1 如图,在梯形ABCD 中,AD ∥BC ,E 是BC 的中点,EF ⊥AB 于F ,EG ⊥CD 于G ,且EF=EG 。
数学学与练52编者:谢正和班级姓名内容:等腰梯形的判定【知识提要】(一)等腰梯形的判定1.两腰相等的梯形是等腰梯形.几何语言表示:∵在梯形ABCD中,AD =BC∴梯形ABCD是等腰梯形.2.同一底上的两个角相等的梯形是等腰梯形.几何语言表示:∵在梯形ABCD中,∠A =∠B∴梯形ABCD是等腰梯形.3.两条对角线相等的梯形是等腰梯形.几何语言表示:∵在梯形ABCD中,AC =BD∴梯形ABCD是等腰梯形.(二)解决梯形问题常用的方法解决梯形问题经常要根据条件添加辅助线,•把梯形转化为平行四边形或三角形问题解决,使一些分散的条件适当集中,再进行解答,学习过程中要注意积累.⑴“作高”:使两腰在两个直角三角形中;⑵“平行腰”:使两条腰在同一个三角形中;⑶“移对角线”:使两条对角线在同一个三角形中;⑷“延腰”:构造具有公共角的两个等腰三角形;⑸“等积变形”,连结梯形上底一端点和另一腰中点,并延长与下底延长线交于一点,构成三角形;【基础训练】一、选择填空题1.下列结论中,正确的是()A.等腰梯形的两个底角相等 B.两个底角相等的梯形是等腰梯形C.一组对边平行的四边形是梯形 D.两条腰相等的梯形是等腰梯形2.如图所示,等腰梯形ABCD的对角线AC,BD相交于点O,则图中全等三角形有()A.2对 B.3对 C.4对 D.5对A3.课外活动课上,•老师让同学们制作了一个对角线互相垂直的等腰梯形形状的风筝,其面积为450cm,则两条对角线所用的竹条长度之和至少为()A..30cm C.60cm D.4.等腰梯形上底,下底和腰分别为4,•10,•5,•则梯形的高为_________.5.一个等腰梯形的上底长为5cm,下底长为12cm,一个底角为60°,则它的腰长为____cm,周长为______cm.6.在四边形ABCD中,AD∥BC,但AD≠BC,若使它成为等腰梯形,则需要添加的条件是__ _____ _ __(填一个正确的条件即可).二、解答题7.如图所示,在等腰梯形ABCD中,AD∥BC,AD=DC,AB⊥AC,求∠BAD的度数C 8.在等腰梯形中,∠A = 150°,AB =10,BC =30,求AD;9.如图,在梯形ABCD中,AD∥BC,AB = 6,BC = 14,CD = 10,AD=6;求证:AB⊥BC.10.如图,在梯形ABCD 中,AD ∥BC ,AB =CD ,AC ⊥BD ,AD =6,BC =8,求梯形的高;11.如图,矩形ABCD 中,点E 、F 在边AD 上,AE =FD .求证:四边形EBCF 是等腰梯形.B12.如图,△ABC 中,AB =AC , DE ∥BC .求证: 四边形DBCE 是等腰梯形.13.如图,E 、F 分别是矩形ABCD 的对角线AC 和BD 上的点,且AE =DF . 求证: 四边形BCFE 是等腰梯形.B14.如图,梯形ABCD 中, AD ∥BC ,对角线AC 、BD 交于点O ,∠1=∠2. 求证: 四边形ABCD 是等腰梯形.【拓展提高】15.如图所示,在直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =24 cm ,BC =26 cm ,动点P 从A 点开始沿AD 边向D 以1 cm /s 的速度移动,动点Q 从C 开始沿CB 边向B 以3 cm /s •的速度移动,P 、Q 分别从点A 、C 同时出发,当其中一点到达顶点时,•另一点也随之停止运动,设运动时间为t (s ),问:(1)t 为何值时,四边形PQCD 为平行四边形? (2)t 为何值时,四边形PQCD 为矩形?(3)t 为何值时,四边形PQCD 为等腰梯形?(列方程求解)QP DC BA。
20.5 等腰梯形的判定一、填空题(每小题2分,共20分)1. 等腰梯形的上底和高相等,下底是上底的3倍,则它的下底上的角是 度。
2. 如图等腰梯形ABCD 中,AB //CD ,AD =BC ,对角线CA 平分∠BCD ,这个梯形的周长为26cm ,AB =6cm ,则CD = cm .D AB(第2题)(第4题)3.如图,梯形ABCD 中,BC AD //,1===AD CD AB ,︒=∠60B 直线MN 为梯形ABCD 的对称轴,P 为MN 上一点,那么PD PC +的最小值 .4.如图,等腰梯形ABCD 中,AD ∥BC ,∠B =45°,AE ⊥BC 于点E ,AE =AD =2 cm ,则这个梯形的中位线长为_____cm .5.等腰梯形的中位线长是15 ,一条对角线平分一个60°的底角,则梯形的周长为_______6.图⑴中的梯形符合____条件时,可以经过旋转和翻折形成图案⑵.7.如图示,是一块待开发的土地,规划人员把它分割成①号区,②号区,③号区三块,拟在①号区种花,②号区建房,③号区种树,已知图中四边形ABCD 与四边形EFGH 是两个相同的直角梯形,则①号区种花的面积是 .(第6题) (第7题) (第9题) 8.顺次连结等腰梯形四边中点所得的四边形是___形;9.如图,等腰梯形ABCD中,AB=DC,对角线AC、BD互相垂直,垂足为O,如果AD=2,BC=4,则梯形ABCD的面积是___;第3题⑴⑵(1)图10(3)(2)ABCDOEF10.如图10是由等长的木棒组成的图案,其中(1)有一个梯形,需要木棒7根;(2)有4个梯形,需要木棒11根;按此规律排列,图(3)有___个梯形,第n个图需要木棒___根.二、选择题(每小题3分,共30分) 11.下面命题错误..的是( ) A.等腰梯形的两底平行且相等B.等腰梯形的两条对角线相等C.等腰梯形在同一底上的两个角相等D.等腰梯形是轴对称图形12.如图,等腰梯形ABCD 中,AB ∥CD ,2AB CD =,AC 交BD 于点O ,点E 、F 分别为AO 、BO 的中点,则下列关于点O 成中心对称的一组三角形是( ). A .ABO CDO ∆∆与 B .AOD BOC ∆∆与 C .CDO EFO ∆∆与 D .ACD BCD ∆∆与 (第12题) (第13题) (第14题) 13.如图,等腰梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,则图中相等的线段共有( )A.2对; B.3对; C.4对; D.5对.14..如图,梯形ABCD中,AD∥BC,分别过AB上的四等分点P、M、R作上下底的平行线PQ,MN,RS分别交DC于Q,N,S,如果PQ=m,RS=n,则AD+BC等于( )A.12(m+n); B.m+n; C.2(m+n); D.4(m+n). 15.如果用两个相同的等腰梯形可以拼成一个菱形,那么这个梯形的腰等于( )A.上底的2倍; B.下底; C.中位线; D.上底与下底的和. 16.如图,M、N分别是梯形ABCD的对角线AC和BD的中点,设梯形两底的长分别是BCDAa、b,则MN等于( ) A.12a; B.12b; C.12(a+b); D.12(b-a).17.设梯形ABCD中,AD∥BC,∠B+∠C=90°,M、N分别是AD和BC的中点,则下列成立的式子是( )A.MN<12(BC-AD); B.MN=12(BC-AD); C.MN>12(BC-AD); D.不能确定.18.如图EF是梯形ABCD的中位线,设图中阴影部分的面积为S,则梯形ABCD的面积是( )A.2S; B.3S; C.4S; D.5S.19.等腰梯形的一个内角为45°,如果较短的底恰好等于梯形的高,那么较长的底是较短底的( ) A.32倍; B.2倍; C.3倍; D.4倍. 20.如图,设梯形ABCD的对角线AC和中位线MN相交于点P,给出以下结论:○1AP=PC;○2AD=2PN;○3BC=2MP;○4MP=2PN,其中正确的个数有( ) A.1个; B.2个; C.3个; D.4个 三、解答题(每题6分,共30分)21. 已知:如图,四边形ABCD 中,AB =DC,AC =DB ,AD ≠BC .求证:四边形ABCD 是等腰梯形.16题18题19题22.已知:如图,在梯形ABCD 中,AD ∥BC ,AB =DC ,P 是AD 中点. 求证:BP =PC .DACPB23.如图,在梯形ABCD 中,AD ∥BC ,AB =DC ,BD ⊥DC 于D ,且∠C =60°,若AD =5 cm ,求梯形的腰长.24.如图,等腰梯形ABCD 中,AD ∥BC ,AB =DC ,AC ⊥BD ,过D 点作DE ∥AC 交BC 的延长线于E 点.⑴求证:四边形ACED 是平行四边形; ⑵若AD =3,BC =7,求梯形ABCD 的面积.A1lBCDA D1C1B125.如图,在直角梯形ABCD 中,AB ∥DC ,∠ABC =90°,AB =2DC ,对角线AC ⊥BD ,垂足为F ,过点F 作EF ∥AB ,交AD 于点E ,CF =4cm . (1)求证:四边形ABFE 是等腰梯形; (2)求AE 的长.四、探索题(每题10分,共20分)26. 如图,已知四边形ABCD 及四边形外一直线l ,四个顶点A 、B 、C 、D 到直线l 的距离分别是a 、b 、c 、d.(1)观察图形,猜想得出a 、b 、c 、d 满足怎样的关系式?证明你的结论. (2)现将l 向上平移,你得到的结论还一定成立吗?请分情况写出你的结论.BA(第25题)CD FE27. 如图,等腰梯形ABCD 中,AD ∥BC ,M 、N 分别是AD 、BC 的中点,E 、F 分别是BM 、CM 的中点.(1)求证:四边形MENF 是菱形;(2)若四边形MENF 是正方形,请探索等腰梯形ABCD 的高和底边BC 的数量关系,并证明你的结论.E D A CF N MB参考答案一、1. 452. 83.3 4.4 5. 50 6. 腰和上底相等,底角为60º7. 396 8. 菱 9. 9 10. 8,(4n+3)二、11.A 12. C 13.D 14.B 15.D 16.D 17.B 18. C 19.C 20.C 三21.如图1 过D点作D E ∥AB 交BC 与点E, 则∠ABE =∠1.∵AB=DC,AC=DB,BC=CB,∴△ABC ≌△DCB (SSS ). ∴∠ABC =∠DCB .∴∠1=∠DCB .∴AB=DC =DE .∴四边形ABED 是平行四边形. ∴AD ∥BC,BE =AD . 又∵AD ≠BC ,∴点E、C 是不同的点,DC 不平行AB . ∴四边形ABCD 是等腰梯形.22. 在梯形ABCD 中,AD ∥BC ,∵ AB =DC ,∴ ∠A =∠D .∵ P 是AD 中点,∴ AP =DP .在△ABP 和△DCP 中,⎪⎩⎪⎨⎧=∠=∠=.,,DP AP D A DC AB ∴ △ABP ≌△DCP .∴ PB =PC .23. ∵ BD ⊥CD ,∠C =60°,∴ ∠CBD =30°.在等腰梯形ABCD 中,∠ABC =∠C =60°,∴ ∠ABD =∠CBD =30°.∵ AD ∥BC ,∴ ∠ADB =∠CBD . ∴ ∠ABD =∠ADB .∴ AB =AD =5(cm ).24. ⑴∵AD ∥BC ∴AD ∥CE 又∵DE ∥AC ∴四边形ACED 是平行四边形 ⑵过D 点作DF ⊥BE 于F 点 ∵DE ∥AC ,AC ⊥BD ∴DE ⊥BD ,即∠BDE =90° 由⑴知DE =AC ,CE =AD=3 ∵四边形ABCD 是等腰梯形 ∴AC =DB ∴DE =DB∴△DBE 是等腰直角三角形,∴△DFB 也是等腰直角三角形O 1D 1C 1B 1DA A 1ClOB∴DF =BF =21(7-3)+3=5 (也可运用:直角三角形斜边上的中线等于斜边的一半“) ()2553721DF BC)(AD 21ABCD =⨯+=∙+=梯形S 25. 过点D 作DG ⊥AB ,垂足为G .在直角梯形ABCD 中,∠DCB =∠CBA =90°. ∵ ∠DGB =90°,∴四边形DGBC 是矩形.∴ DC =BG .∵ AB =2CD ,∴AG =GB .∴ DA =DB ,∴ ∠DAB =∠DBA .又∵ EF ∥AB ,AE 与BF 相交于D 点,∴ 四边形ABFE 是等腰梯形.(2)解:∵ CD ∥AB ,∴CD CFAB AF=.∵ AB =2CD ,∴ AF =2CF . ∵ CF =4,∴AF =8. ∵ ∠CBA =90°,AC ⊥BF ,∴ Rt △BCF ∽Rt △ABF . ∴CF BFBF AF=,∴ BF 2=CF ·F A =4×8=32.∴BF =4 2 . ∵四边形ABFE 是等腰梯形,∴ AE = BF = 4 2 (cm ). 四、26. (1)a+c=b+d.证明:连结AC 、BD ,且AC 、BD 相交于O 点,OO 1为直角梯形BB 1D 1D 的中位线.所以2001=DD 1+BB 1=b+d ,同理2001=AA 1+CC 1=a+c , 所以a+c=b+d.(2)不一定成立.分别以下几种情况:①直线l 过A 点时,c=b+d ; ②直线l 过A 点与B 点之间时,c-a=b+d ;③直线过B 点时,c-a=d ;④直线l 过B 点与D 点之间时,a-c=b-d ; ⑤直线l 过D 点时,a-c=b ;⑥直线l 过C 点与D 点之间时,a-c=b+d ; ⑦直线l 过C 点时,a=b+d ;⑧直线l 在C 点上方时,a+c=b+d.27. (1)因为四边形ABCD 为等腰梯形,所以AB=CD ,∠A=∠D ,因为M 为AD 的中点,所以AM=DM ,所以△ABM ≌△DCM ,所以BM=CM.BA(第25题)CD FEG因为E 、F 为MB 、CM 中点,BE=EM ,MF=FC ,N 为BC 的中点, 所以EN=FN=FM=EM ,所以四边形ENFM 是菱形.(2) 连接MN ,因为BM=CM ,BN=NC ,所以MN ⊥BC ,所以MN 是梯形ABCD 的高,又四边形MENF 是正方形,所以△BMC 是直角三角形, 又N 是BC 的中点,所以MN =21BC .。