当前位置：文档之家 › 材料力学B试题7应力状态_强度理论.

材料力学B试题7应力状态_强度理论.

  • 格式：doc
  • 大小：582.00 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

材料力学考试题

材料力学考试题

2010—2011材料力学试题及答案A一、单选题（每小题2分，共10小题，20分）1、工程构件要正常安全的工作，必须满足一定的条件。

下列除（）项，其他各项是必须满足的条件。

A、强度条件B、刚度条件C、稳定性条件D、硬度条件2、内力和应力的关系是（）A、内力大于应力B、内力等于应力的代数和C、内力是矢量，应力是标量D、应力是分布内力的集度3、根据圆轴扭转时的平面假设，可以认为圆轴扭转时横截面（）。

A、形状尺寸不变，直径线仍为直线。

B、形状尺寸改变，直径线仍为直线。

C、形状尺寸不变，直径线不保持直线。

D、形状尺寸改变，直径线不保持直线。

4、建立平面弯曲正应力公式zIMy=σ,需要考虑的关系有（）。

A、平衡关系,物理关系，变形几何关系；B、变形几何关系，物理关系，静力关系；C、变形几何关系，平衡关系，静力关系；D、平衡关系, 物理关系，静力关系；5、利用积分法求梁的变形，不需要用到下面那类条件（）来确定积分常数。

A、平衡条件。

B、边界条件。

C、连续性条件。

D、光滑性条件。

6、图示交变应力的循环特征r、平均应力mσ、应力幅度aσ分别为（）。

A -10、20、10；B 30、10、20；C 31-、20、10；D 31-、10、20 。

7、一点的应力状态如下图所示，则其主应力1σ、2σ、3σ分别为（）。

A 30MPa、100 MPa、50 MPa B 50 MPa、30MPa、-50MPa C 50 MPa、0、-50Mpa、 D -50 MPa、30MPa、50MPa8、对于突加载的情形，系统的动荷系数为（）。

A、2B、3C、4D、59、压杆临界力的大小，（）。

A与压杆所承受的轴向压力大小有关； B 与压杆的柔度大小有关； C 与压杆材料无关； D 与压杆的柔度大小无关。

10、利用图乘法计算弹性梁或者刚架的位移，要求结构满足三个条件。

以下那个条件不是必须的（）A、EI为常量B、结构轴线必须为直线。

C、M图必须是直线。

材料力学第七章应力状态和强度理论

材料力学第七章应力状态和强度理论
2
x y 2 a 0 2
x y x y 2
x y
2
) x
2
2
例题1: 已知:单元体各侧面应力 x=60MPa,
求: (1) = - 450斜截面上的应力,(2)主应力和主平面
dA
y

x y
2
sin 2 xy cos2
y
yx
应力圆
y
1 R 2

x
y

2
4 2 xy
x
yx xy x
y
R c

x y
2
2
x
xy
x´
dA
yx
y´
y
x y 1 2 2 2

40

x y
2 0.431MPa
sin( 80 ) xy cos(80 )

C
C

C
例题3：已知梁上的M、Q，试用单元体表示截面上1、2、
3、4点的应力状态。
1
2 0
2
1点 2点
1 2 0 3
3Q ＝ 2A
M x Wz
2 xy
x y
2 20.6 0.69 60 0
17.2
x y
2 (
6.4MPa
2 34.4
max(min)
x
17.20
x y
2
) xy
2
2
x
66.4MPa
60 0 60 0 2 ( ) 20.6 2 2 2 66.4(6.4) MPa

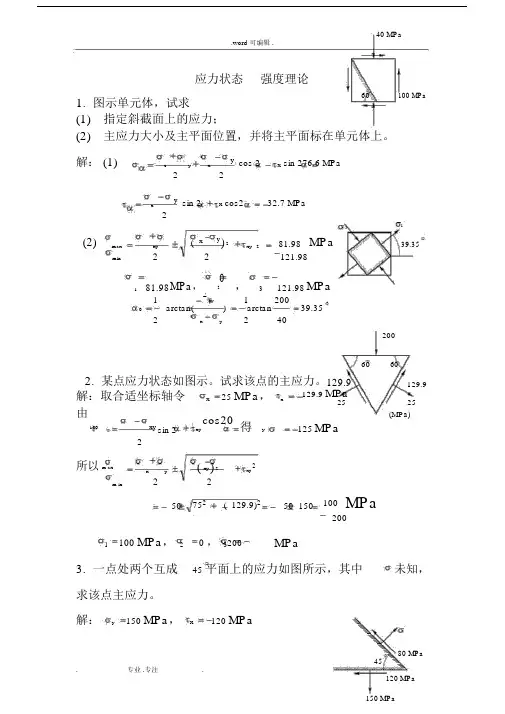
材料力学B试题7应力状态_强度理论.docx

材料力学B试题7应力状态_强度理论.docx

40 MPa.word 可编辑 .应力状态强度理论1. 图示单元体，试求60100 MPa(1)指定斜截面上的应力；(2)主应力大小及主平面位置，并将主平面标在单元体上。

解： (1)x y xy cos 2x sin 276.6 MPa22xy sin 2x cos232.7 MPa231 (2)max xy( x y) 2xy281.98MPa39.35min22121.98181.98MPa，2，3121.98MPa12xy12000arctan()arctan39.352x y24020060602. 某点应力状态如图示。

试求该点的主应力。

129.9129.9解：取合适坐标轴令x25 MPa，x由120xy sin 2xy cos20 得y2所以m axx y( xy ) 2xy 2m in 22129.9 MPa2525(MPa)125MPa50752( 129.9)250 150100 MPa2001 100MPa，20 ，3200MPa3. 一点处两个互成45 平面上的应力如图所示，其中未知，求该点主应力。

解：y150 MPa，x120 MPa.word 可编辑 .由得45xy sin 2xy cos 2x 15080 22x10MPa所以max xy(x y)2222xy min yx454545214.22 MPa 74.221214.22 MPa，20 ，45374.22MPa4.图示封闭薄壁圆筒，内径 d 100 mm，壁厚 t 2 mm，承受内压 p 4 MPa，外力偶矩 M e 0.192 kN·m。

求靠圆筒内壁任一点处的主应力。

0.19210 3解：xπ(0.10440.14)0.05 5.75MPat32x y pd MPa504tpd MPa1002tM e p M emax x y(x y ) 2xy2min22100.7 MPa 49.351100.7MPa，249.35 MPa，3 4 MPa5.受力体某点平面上的应力如图示，求其主应力大小。

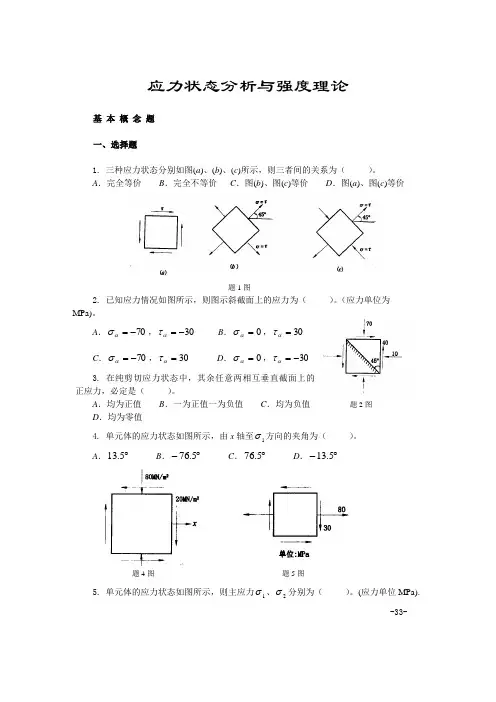
材料力学习题应力状态和强度理论

材料力学习题应力状态和强度理论

应力状态分析与强度理论基 本 概 念 题一、选择题1. 三种应力状态分别如图(a )、(b )、(c )所示，则三者间的关系为（ ）。

A ．完全等价B ．完全不等价C ．图(b )、图(c )等价D ．图(a )、图(c )等价题1图2. 已知应力情况如图所示，则图示斜截面上的应力为（ ）。

（应力单位为 MPa)。

A ．70-=ασ，30-=ατB ．0=ασ，30=ατC ．70-=ασ，30=ατD ．0=ασ，30-=ατ3. 在纯剪切应力状态中，其余任意两相互垂直截面上的 正应力，必定是（ ）。

A ．均为正值B ．一为正值一为负值C ．均为负值 题2图D ．均为零值4. 单元体的应力状态如图所示，由x 轴至1σ方向的夹角为（ ）。

A ．︒5.13 B ．︒-5.76 C ．︒5.76 D ．︒-5.13题4图 题5图5. 单元体的应力状态如图所示，则主应力1σ、2σ分别为（ ）。

(应力单位MPa). -33-A ．901=σ，102-=σB ．1001=σ，102-=σC ．901=σ，02=σD ．1001=σ，02=σ 6. 如图6所示单元体最大剪应力m ax τ为（ ）。

A ．100 MPaB ．50 MPaC ．25 MPaD ．0题6图 题7图7. 单元体如图所示，关于其主应力有下列四种答案，正确的是（ ）。

A ．1σ＞2σ，03=σ B ．3σ＜2σ＜0，03=σ01=σ C ．1σ＞0，2σ= 0，3σ＜0，1σ＜3σ D ．1σ＞0，2σ= 0，3σ＜0，1σ＞3σ8. 已知应力圆如图7-22所示，图(a )、(b )、(c )、(d )分别表示单元体的应力状态和A 截面的应力，则与应力圆所对应的单元体为( )。

A ．图(a )B ．图(b )C ．图(c )D ．图(d )题8图9. 在图示四种应力状态中，其应力圆具有相同的圆心和相同的半径是（ ）。

-34-题9图A ．图(a )、图(d )B ．图(b )、图(c )C ．图(a )、图(b )、图(c ) 、图(d )D ．图(a )、图(d )、图(b )、图(c )10. 如图所示，较大体积的钢块上开有一贯穿的槽，槽内嵌入一铝质立方体，铝块受到均布压力P 作用，假设钢块不变形，铝块处于（ ）。

材料力学 第07章 应力状态分析与强度理论

材料力学 第07章 应力状态分析与强度理论
2
sin2a t xy cos2a
18/95
7.2 平面应力状态分析 主应力 7.2.3 主平面的方位及极值正应力 s x s y s x s y sa cos2a t xy sin2a 2 2 s x s y ds a 上式对a 求导 2 sin2a t xy cos2a da 2 s x s y 若a a0时，导数为 0 sin2a 0 t xy cos2a 0 0 2 2t xy tan2a 0 s x s y
7.2.5 应力圆
t
sx
tyx
sy
sx txy sy
D(sx,txy) 1. 确定点 D (s ,t ) x xy
O
D'(sy,tyx)
C
s
2. 确定点D' (sy,tyx) tyx= －txy 3. 连接DD'与s 轴交于点C 4. 以 C 为圆心，CD（CD'） 为半径画圆。
26/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆
sx sy sz
sxs1 100 MPas 2
0 MPas 3 120 MPa
11/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态 三个主应力中仅有一个主应力不为零 单向应力状态
s1
s1
F
A
F
12/95
7.1 一点的应力状态的概念 单向、二向(平面)、三向(空间)应力状态
O
D'(sy,tyx)
C sx－ sx sy/2
s
27/95
7.2 平面应力状态分析 主应力 7.2.5 应力圆 利用应力圆确定角a 斜截面上的正应力和切应力

工程力学c材料力学部分第七章 应力状态和强度理论

工程力学c材料力学部分第七章 应力状态和强度理论

无论是强度分析还是刚度分析，都需要求出应力的极值， 无论是强度分析还是刚度分析，都需要求出应力的极值，为了找 到构件内最大应力的位置和方向 需要对各点的应力情况做出分析。 最大应力的位置和方向， 到构件内最大应力的位置和方向，需要对各点的应力情况做出分析。
受力构件内一点处所有方位截面上应力的集合，称为一点的 受力构件内一点处所有方位截面上应力的集合，称为一点的 研究一点的应力状态时， 应力状态 。研究一点的应力状态时，往往围绕该点取一个无限小 的正六面体—单元体来研究。 单元体来研究 的正六面体 单元体来研究。
σ2
σ2
σ1
σ1
σ
σ
σ3
三向应力状态
双向应力状态
单向应力状态 简单应力状态
复杂应力状态 主应力符号按代数值的大小规定： 主应力符号按代数值的大小规定：
σ1 ≥ σ 2 ≥ σ 3
平面应力状态的应力分析—解析法 §7−2 平面应力状态的应力分析 解析法
图(a)所示平面应力单元体常用平面图形(b)来表示。现欲求 )所示平面应力单元体常用平面图形( )来表示。现欲求 垂直于平面xy的任意斜截面 上的应力 垂直于平面 的任意斜截面ef上的应力。 的任意斜截面 上的应力。
二、最大正应力和最大剪应力
σα =
σ x +σ y
2
+
σ x −σ y
2
cos 2α − τ x sin 2α
τα =
令
σ x −σ y
2
sin 2α + τ x cos 2α
dσ α =0 dα
σ x −σ y
2
sin 2α +τ x cos2α = 0
可见在 τ α
=0

材料力学习题参考答案2011年7月-第22章应力状态和强度理论

材料力学习题参考答案2011年7月-第22章应力状态和强度理论

22-６ 图示受力板件，试证明A 点处各截面的正应力、剪应力均为零证明：若在尖点A 处沿自由边界取三角形单元体如图所示，设单元体 、面上的应力分量为、和、，自由边界上的应力分量为，则有由于、，因此，必有、、。

这时，代表A 点应力状态的应力圆缩为 坐标的原点，所以A 点为零应力状态。

22-7 图示槽形刚体，在槽内放置一边长为10mm 、的立方钢块，钢块顶面受到合力为P=8kN 的均布压力作用，试求钢块的三个主应力和最大剪应力。

已知材料的弹性模量GPa E 200=，泊松比3.0=μ。

解： 选取坐标轴x 、y 、z 如图。

x σ＝0， σz ＝－10101083⨯⨯＝－80MPa ，εy ＝1E 〔σy －μ（σz ＋σx ）〕＝1E〔σy －μσz 〕＝0 由此得 σy ＝μσz ＝0.3×（－80）=－24 MPa 。

Ｐxzyo将x σ、y σ、z σ按代数值大小排列，得三个主应力为 σ1＝0 、σ2 ＝－24 MPa 、σ3=－80 MPa 。

最大剪应力 τm a x =σσ132-＝280＝40 MPa 。

22-12 试比较图示正方形棱柱体在下列两种情况下的相当应力3xd σ：(a )棱柱体自由受压：(b )棱柱体在刚性方模内受压。

弹性常数E 、μ均为已知.解：对于图（a ）中的情况，应力状态如图（c ）对于图（b ）中的情况，应力状态如图（d ）所以，，22-20 N O.28a普通热轧工字钢简支梁如图所示。

今由贴在中性层上某点K处、与轴线夹45º角方向上的应变片测得ε45º=-260×10-6。

已知钢材的E=210GPa，μ=0.28。

求作用在梁上的载荷F P。

《材料力学》第7章-应力状态和强度理论-习题解

《材料力学》第7章-应力状态和强度理论-习题解
解：左支座为A，右支座为B，左集中力作用点为C，右集中力作用点为D。
支座反力: (↑)
=
（1）梁内最大正应力发生在跨中截面的上、下边缘
超过 的5。3％，在工程上是允许的。
（2）梁内最大剪应力发生在支承截面的中性轴处
(3)在集中力作用处偏外侧横截面上校核点a的强度
超过 的3.53%，在工程上是允许的。
解：坐标面应力:X（—0。05，0);Y（-0.2,0）
。根据以上数据作出如图所示的应
力圆。图中比例尺为 代表 。
按比例尺量得斜面的应力为：
按习题7—5得到的公式计算如下：
作图法(应力圆法)与解析法（公式法）的结果一致。
［习题7-7]试用应力圆的几何关系求图示悬臂梁距离自由端为 的截面上，在顶面以下 的一点处的最大及最小主应力,并求最大主应力与 轴之间的夹角。
解：
…………(1)
…………（2)
（1)、(2)联立,可解得 和 。
至此,三个面的应力均为已知：X（ ，0），Y（ ，0）（ , 均为负值）;
( ）。由X，Y面的应力就可以作出应力圆。
[习题7-12]一焊接钢板梁的尺寸及受力情况如图所示,梁的自重略去不计。试示 上 三点处的主应力。
解:（1）求 点的主应力
解：坐标面应力：X（15,15）,Y(0，-15）
第一强度理论：
因为 ， ，即 ，
所以 符合第一强度理论的强度条件，构件不会破坏，即安全.
第二强度理论：
因为 ,
，即 ，
所以 符合第二强度理论的强度条件，构件不会破坏，即安全。
[习题7—25]一简支钢板梁承受荷载如图a所示，其截面尺寸见图b。已知钢材的许用应力为 , .试校核梁内的最大正应力和最大切应力。并按第四强度理论校核危险截面上的a点的强度。注:通常在计算a点处的应力时，近似地按 点的位置计算。

材料力学试题带答案B

材料力学试题带答案B

试卷类型：B 卷一、判断题（判断以下论述的正误，认为正确的就在答题相应位置划“T”，错误的划“F”。

每小题 1分，共10 分）1.材料力学主要研究杆件受力后变形与破坏的规律。

（）2.工程构件正常工作的条件是必须同时满足必要的强度、刚度和稳定性。

（）3.由切应力互等定理可知，在相互垂直平面上，切应力总是成对出现，且数值相等，方向则共同指向该两平面的交线。

（）4.截面法是分析应力的基本方法。

（）5.只有静不定结构才可能有温度应力和装配应力。

（）6.圆轴扭转时，横截面上既有正应力，又有剪应力。

（）7.截面的主惯性矩是截面对通过该点所有轴的惯性矩中的最大值和最小值。

（）8.梁端铰支座处无集中力偶作用，该端的铰支座处的弯矩必为零。

（）9.若集中力作用处，剪力有突变，则说明该处的弯矩值也有突变。

（）10.在平面图形的几何性质中，静矩和惯性积的值可正、可负、也可为零。

（）二、填空题（本题共有10个空，填错或不填均不能得分。

每空2分，共20分）1.基本变形中：轴向拉压杆件横截面上的内力是，扭转圆轴横面上的内力是，平面弯曲梁横截面上的内力是和。

2.图所示铆钉联接件将发生挤压与剪切破坏，铆钉所受剪应力大小为，接触面上的挤压应力为。

(a)(b)PP3.EA称为材料的。

4.图示正方形截面简支梁，若载荷不变而将截面边长增加一倍，则其最大弯曲正应力为原来的倍，最大弯曲剪应力为原来的倍。

5.剪切的胡克定律表明：当应力不超过材料的pτ时，切应力τ与切应变γ成比例关系。

三、单项选择题（从下列各题四个备选答案中选出一个正确答案，并将其代号写在答题纸的相应位置。

答案选错或未选者，该题不得分。

每小题2分，共20分）1.下列结论中，只有哪个是正确的 。

A 材料力学的任务是研究材料的组成分析； B 材料力学的任务是研究各种材料的力学性能；C 材料力学的任务是在保证安全的原则下设计结构的构件；D 材料力学的任务是在即安全又经济的原则下，为设计结构构件提供分析计算的基本理论和方法。

材料力学 第七章 应力状态和强度理论

材料力学 第七章 应力状态和强度理论

y
2
2 xy
tan 2a0
2 xy x
y
max
1
2
3
主应力符号与规定： 1 2 3 （按代数值）
§7-3 空间应力状态
与任一截面相对应 的点，或位于应力 圆上，或位于由应 力圆所构成的阴影 区域内
max 1 min 3
max
1
3
2
最大切应力位于与 1 及 3 均成45的截面上
针转为正，顺时针转为负。
tg 2a 0
2 x x
y
在主值区间，2a0有两个解，与此对应的a0也有两个解，其中落
在剪应力箭头所指象限内的解为真解，另一解舍掉。
三、应力圆
由解析法知，任意斜截面的应力为
a
x y
2
a x
x
y
2
y cos2a
2
sin 2a x c
x s os2a
in
2a
广义胡克定律
1、基本变形时的胡克定律
1）轴向拉压胡克定律
x E x
横向变形
y
x
x
E
2）纯剪切胡克定律
G
y
x x
2、三向应力状态的广义胡克定律－叠加法
2
2
1
1
3
3
1
1
E
2
E
3
E
1
1 E
1
2
3
同理
2
1 E
2
3
1
广义胡克定律
3
1 E
3
1
2
7-5, 7-6
§7-4 材料的破坏形式
⒈ 上述公式中各项均为代数量，应用公式解题时，首先应写清已 知条件。

《材料力学》第1到8章复习题

《材料力学》第1到8章复习题

材料力学第一章复习题1，下列结论中正确的是（）A,内力是应力的代数和B,应力是内力的平均值C应力是内力的集度D内力必大于应力2. 一对自平衡的外载产生杆件的哪种基本变形只对杆件的某一局部存在影响。

( )A 拉伸与压缩B 剪切C扭转D弯曲3，已设计好的构件，若制造时仅对其材料进行更换通常不会影响其( )A稳定性 B 强度C几何尺寸D刚度4. 根据均匀性假设，可认为构件的下列各量中的( )在各点处都相同A屈服极限B材料的弹性常数C应力D应变第二章轴向拉伸压缩与剪切挤压的实用计算1.塑性材料的极限应力是A屈服极限B强度极限c比例极限D弹性极限2.脆性材料的极限应力是。

A屈服极限B比例极限C强度极限D弹性极限3.受轴向拉压的杆件内最大切应力为80 Mpa，则杆内最大正应力等于A160Mpa B 80Mpa C40Mpa D20Mpa4.在低碳钢Q235的拉伸试验中，材料暂时失去了抵抗变形能力是发生在哪个阶段A弹性B屈服C强化D缩颈断裂5材料进入强化阶段卸载，在室温中放置几天再重新加载可以获得更高的()。

A比例极限B强度极限C弹性变形D塑性变形6直径为d的圆截面钢杆受轴向拉力作用，已知其纵向线应变为e，弹性模量为E，杆轴力大小为()。

填空题(5.0分)7.在连接件上，剪切面和挤压面分别（)于外力方向8.连接件剪切强度的实用计算中去，许用切应力是由( )9.插销穿过水平放置的平板上的圆孔，在其下端受拉力F作用。

该插销的剪切面面积和挤压面面积分别等于( a)。

填空题(5.0分)10.低碳钢拉伸试验中滑移线是( )造成的。

11.外力消失后，变形也消失,这种变形为( )12.当延伸率小于( )时为脆性材料，当延伸率大于( )时为塑性材料13.一个结构中有三根拉压杆，设由这三根杆的强度条件确定的结构许用载荷分别为F1、F2、F3，且F1<F2<F3，则该结构的实际许可载荷[F]为判断题(5.0分)14低碳钢的抗拉能力小于抗剪能力（）A对 B 错15. 试求图中1-1，2-2，3-3截面上的轴力，并作轴力图。

德州学院,材料力学,期末试题7章习题讲解

德州学院,材料力学,期末试题7章习题讲解

德州学院,材料⼒学,期末试题7章习题讲解第七章⼒和应变分析强度理论 §7.1应⼒状态概述1.过受⼒构件内⼀点，取截⾯的不同⽅位，这⼀点在各个⾯上的（D ）. （A ）正应⼒相同，切应⼒不同；（B ）正应⼒不同，切应⼒相同；（C ）正应⼒和切应⼒都相同；（D ）正应⼒和切应⼒都不同。

2.关于单元体的描述，下列正确的是A（A ）单元体的三维尺⼨必须是微⼩的；（B ）单元体是平⾏六⾯体；（C ）单元体必须是正⽅体；。

（D ）单元体必须有⼀对横截⾯。

3.对于图⽰承受轴向拉伸的锥形杆上的A 点，哪⼀种应⼒状态是正确的Dxτxx4.在单元体的主平⾯上（）。

（A ）正应⼒⼀定最⼤；（B ）正应⼒⼀定为零；（C）切应⼒⼀定最⼩；（D ）切应⼒⼀定为零。

§7.2⼆向应⼒状态实例1. Q235钢制成的薄壁圆筒形蒸汽锅炉，壁厚δ，内径D ，蒸汽压⼒p ，试计算锅炉壁内任意⼀点处的三个主应⼒。

注：薄壁圆筒受⼒均匀，因此，任意点的应⼒状态均相同。

1.求⽔平⽅向上的正应⼒σx2.求竖直⽅向上的正应⼒σy3.求垂直于纸⾯⽅向上的正应⼒σz 薄壁圆筒与纸⾯垂直⽅向上的σz 为零.总结：薄壁圆筒的三个主应⼒为：薄壁圆筒为两向应⼒状态注意事项：1.注意单位配套使⽤；2. 纵向截⾯上正应⼒是横截⾯正应⼒的两倍；3.按规定排列正应⼒。

课本215页例7.1如下由Q235钢制成的蒸汽锅炉，壁厚δ=10mm，内径D=1m，蒸汽压⼒p=3MPa，试计算锅炉壁内任意⼀点处的三个主应⼒。

经分析，薄壁圆筒为两向应⼒状态2. 圆球形容器的壁厚为δ，内径为D，内压为p，求容器内任意⼀点的应⼒。

注：薄壁圆球受⼒均匀，因此，任意点的应⼒状态均相同。

1.求⽔平⽅向上的正应⼒σx2.求竖直⽅向上的正应⼒σy3.求垂直于纸⾯⽅向上的正应⼒σz薄壁圆筒与纸⾯垂直⽅向上的σz为零.球形薄壁容器的三个主应⼒为：受内压的球形薄壁容器为⼆向应⼒状态§7.3 ⼆向应⼒状态分析——解析法⼆向应⼒状态下，单元体各⾯上应⼒分量皆为已知，如下图所⽰：求垂直于xy平⾯的任意斜截⾯ef上的应⼒及主应⼒和主平⾯⼀.符号规定1.正应⼒正负号规定2.切应⼒正负号规定使微元或其局部顺时针⽅向转动为正；反之为负。

家电公司研发部资料材料力学习题答案(七)

家电公司研发部资料材料力学习题答案(七)

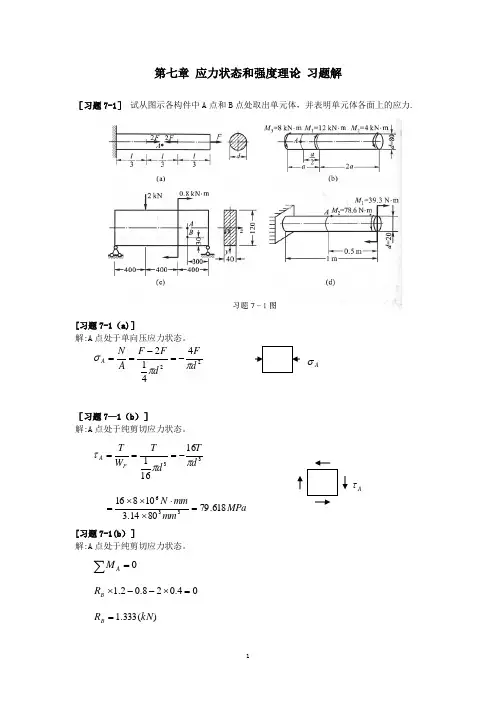
第七章 应力状态和强度理论7-1 围绕受力构件内某点处取出的微棱柱体的平面图如图所示，已知该点处于平面应力状态，AC 面上的正应力σ＝－14MPa ，切应力为零，试从平衡方程确定σx 和τx 值。

答：σx ＝37.9MPa ,τx ＝74.2MPa 解：利用公式求解x x x x x cos 2sin 222sin 2cos 22yyyαασσσσσατασστατα+-=+--=+代入数据得x x x x x 9292140.3430.94229200.940.3432σστστ+--=+⨯-⨯-=⨯+⨯σx ＝37.9MPa ,τx ＝74.2MPa7-2 试绘出图示水坝内A 、B 、C 三小块各截面上的应力（只考虑平面内受力情况）。

A: B: C:7-3 已知平面应力状态如图所示，已知σx ＝100MPa ，σy =40MPa,以及该点处的最大主应力σ1＝120MPa ，试用应力圆求该点处的τx 及另外两个主应力σ2，σ3和最大剪应力τmax。

答：MPa,60,0MPa,20max 32===τσσx τ＝40 MPa 解：由应力圆分析可得A BC题 7 - 2 图题 7 - 1 图111(100,),(40,),(,0)x x c D D C ττσ'-x 121004070MPa221207050MPa 705020MPayc c c r r σσσσσσσ++====-=-=∴=-=-=是平面应力状态3=0σ∴222x x 13max (100)40MPa120060MPa 22c r σττσστ∴=-+⇒=--===7-4 已知平面应力状态一点处互相垂直平面上作用有拉应力90MPa 和压应力50MPa ，这些面上还有剪应力，如果最大主应力为拉应力100MPa ，试求：(1) 上述面上的切应力； (2) 此平面上另一主应力； (3) 最大切应力平面上的正应力； (4) 最大切应力。

[材料力学]材料力学试题库精选题解精选题8_应力状态_强度理论.docx

[材料力学]材料力学试题库精选题解精选题8_应力状态_强度理论.docx

应力状态强度理论1.图示单元体，试求 (1) 指定斜截而丄的应力；(2) 主应力大小及主平而位置，并将主平而标在单元体上。

F<T r — CT V解：(1) (y (/ = — ----- + ---------- cos 2a 一 g sin 2& = 76.6 MPar r/ = ----- sin + r v cos2a =-32.7 MPaCc£X-50 ± 加 +(—129.9)2 = _50 ±1506=100 MPa, (r 2 = 0 , 6=-200 MPa解：b 、=150 MPa,「=—120 MPayx由 r = ----------- sin 2Q +「cos 2a = —~~— = -804522得 6 =-10 MPa3.—点处两个互成45°平面上的应力如图所示,其屮<7未知，求该点主应力。

max bmin81.98 MPa-121.98a = 81.98 MPa, <r 2 = 0 , cr 3 = -121.98 MPa^0=larctan(^^) = l arctan2 CT X -cr v 2402.某点应力状态如图示。

试求该点的主应力。

解：取合适坐标轴令6=25 MPa, r x =-129.9 MPa120"-- ----- sin 2a + T cos 2a = 0 得 = -125 MPa 2 -100MPa-200150 MPacr cr + cr所以max= __ ±2214.22MPa一74.226=214.22 MPa, cr2 = 0, <r3 = -74.22 MPa4.图示封闭薄壁圆筒，内径d=100 mm,壁厚f = 2 mm,承受内床“ =4 MPa, 外力偶矩M“=0・192 kN-mo求靠圆筒内壁任一点处的主应力。

解・・r常九严停32a=^- = 5Q MPax 4t<r v二四= 100 MPa、2tmax bmin 100.7MPa 49.356=100.7 MPa, 6=49.35 MPa, (r3 = -4 MPa5.受力体某点平面JL的应力如图示，求其主应力大小。

材料力学习题册答案-第7章-应力状态知识讲解

材料力学习题册答案-第7章-应力状态知识讲解

材料力学习题册答案-第7章-应力状态第七章应力状态强度理论一、判断题1、平面应力状态即二向应力状态，空间应力状态即三向应力状态。

(√)2、单元体中正应力为最大值的截面上，剪应力必定为零。

(√)3、单元体中剪应力为最大值的截面上，正应力必定为零。

(×) 原因：正应力一般不为零。

4、单向应力状态的应力圆和三向均匀拉伸或压缩应力状态的应力圆相同，且均为应力轴上的一个点。

(×)原因：单向应力状态的应力圆不为一个点，而是一个圆。

三向等拉或等压倒是为一个点。

5、纯剪应力状态的单元体，最大正应力和最大剪应力值相等，且作用在同一平面上。

(×)原因：最大正应力和最大剪应力值相等，但不在同一平面上6、材料在静载作用下的失效形式主要有断裂和屈服两种。

(√)7、砖,石等脆性材料式样压缩时沿横截面断裂。

(×)8、塑性材料制成的杆件，其危险点必须用第三或第四强度理论所建立的强度条件来校核强度。

(×) 原因：塑性材料也会表现出脆性，比如三向受拉时，此时，就应用第一强度理论9、纯剪应力状态的单元体既在体积改变，又有形状改变。

(×)原因：只形状改变，体积不变10、铸铁水管冬天结冰时会因冰膨胀被胀裂，而管内的冰不会被破坏，只是因为冰的强度比铸铁的强度高。

(×)原因：铸铁的强度显然高于冰，其破坏原因是受到复杂应力状态二、 选择题1、危险截面是（ C ）所在的截面。

A 最大面积B 最小面积C 最大应力D 最大内力2、关于用单元体表示一点处的应力状态，如下论述中正确的一种是( D )。

A 单元体的形状可以是任意的B 单元体的形状不是任意的，只能是六面体微元C 不一定是六面体，五面体也可以，其他形状则不行D 单元体的形状可以是任意的，但其上已知的应力分量足以确定任意方向面上的硬力3、受力构件内任意一点，随着所截取截面方位不同，一般来说（ D ） A 正应力相同，剪应力不同 B 正应力不同，剪应力相同 C 正应力和剪应力均相同 D 正应力和剪应力均不同4、圆轴受扭时，轴表面各点处于（ B ）A 单向应力状态B 二向应力状态C 三向应力状态D 各向等应力状态 5、分析处于平面应力状态的一点，说法正确的是（ B ）。

第十二章 应力状态和强度理论习题

第十二章 应力状态和强度理论习题
（3）求出该点的主应力与主平面位置（并在单元体上画出）。
试题答案：
解：(1)
(2)
(3)
， ，
8、求图示木梁截面 上点 与轴线成 角方向的线应变 。已知 ， ， ，材料的弹性模量 ，泊松比 。
试题答案：
解：在点B，正应力为零，只有切应力，为纯剪切应力状态。
，
9、设地层由石灰岩组成，其密度 ，泊松比 。计算离地面 深处的地压应力。
（2）
（3）
12、受内压的薄壁圆筒，已知内压为 ，平均直径为 ，壁厚为 ，弹性常数为 、 。试确定圆筒薄壁上任一点的主应力、主应变及第三、第四强度理论的相当应力。
解： ， ，
13、构件中危险点的应力状态如图所示。试选择合适的准则对以下两种情形作强度校核：1．构件为钢制
= 45MPa， = 135MPa， = 0， = 0，
1、层合板构件中微元受力如图所示，各层板之间用胶粘接，接缝方向如图中所示。若已知胶层剪应力不得超过1MPa。试分析是否满足这一要求。
解：
MPa
MPa，不满足。
2从构件中取出的微元受力如图所示，其中AC为无外力作用的自由表面。试求：x和xy。
解：应用应力解析公式，有
MPa
据此，解得
MPa
Mpa
3、已知一点的应力状态如图。试求其主应力及其方向角，并确定最大切应力值。
许用应力 = 160MPa。
2．构件材料为铸铁
= 20MPa， =25MPa， = 30MPa， = 0， = 30MPa。
解：
1． 强度满足。
2． 强度满足。
14、炮筒横截面如图示。在危险点处 ， ，第二个主应力 ，且垂直于图面。材料的 ，试用第三强度和第四强度理论进行强度校核。

材料力学 第七章 应力状态与强度理论

材料力学 第七章 应力状态与强度理论

取三角形单元建立静力平衡方程
n 0
dA ( xdA cos ) sin ( xdA cos ) cos ( y dA sin ) cos ( y dA sin ) sin 0
t 0
dA ( xdA cos ) cos ( xdA cos ) sin ( y dA sin ) sin ( y dA sin ) cos 0
2 2

cos 2 x sin 2
2 x y 2 x y ( ) ( cos 2 x sin 2 )2
2
2

x y
sin 2 x cos 2
( 0) (
x y
2
2
sin 2 x cos 2 )
max x y x y 2 x 2 2 min
2
max
1 3
2
例7-2 试求例7-1中所示单元体的主应力和最大剪应力。
（1）求主应力的值
x 10MPa, y 30MPa, x 20MPa max x y x y 2 2 x min 2
复杂应力状态下（只就主应力状态说明） 有三个主应力
1 , 2 , 3
1
E
由 1引起的线段 1应变 1
由 2引起的线段 1应变 1
2
由 3引起的线段1应变 1
3
E
E
沿主应力1的方向的总应变为：
1 1 1 1
1 42.4 1 3 2 0 MPa 由 max 3 2.4 2

材料力学-07-应力分析和强度理论

材料力学-07-应力分析和强度理论

§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法： 解析法
1.斜截面上的应力 1.斜截面上的应力
y
σx
a
τ yx
τ xy
σx α
τa
n
τ xy
σa
dA
x
σy
n
τ yx
σy
t
t
∑F = 0
∑F =0
13
§7-2 平面应力状态 平面应力状态--解析法 平面应力状态 解析法： 解析法
tan 2α0 = − 2τ xy
σ x −σ y
由上式可以确定出两个相互垂直的平面， 由上式可以确定出两个相互垂直的平面，分别 为最大正应力和最小正应力所在平面。 为最大正应力和最小正应力所在平面。 所以，最大和最小正应力分别为： 所以，最大和最小正应力分别为：
σmax = σ x +σ y
2 1 + 2 − 1 2
单元体
单元体——构件内的点的代表物， 单元体——构件内的点的代表物，是包围被研究点的 ——构件内的点的代表物 无限小的几何体。 常用的是正六面体。 无限小的几何体。 常用的是正六面体。 单元体的性质—— 平行面上，应力均布； 单元体的性质——1) 平行面上，应力均布； —— 2) 平行面上，应力相等。 平行面上，应力相等。
2 2
σy
τ xy
α
60 − 40 60 + 40 = + cos(−60o ) + 30 sin(−60o ) 2 2
σx
= 9.02 MPa
τα =
σ x −σ y
2 60 + 40 = sin(−60o ) − 30 cos(−60o ) 2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

应力状态 强度理论1. 图示单元体，试求(1) 指定斜截面上的应力；(2) 主应力大小及主平面位置，并将主平面标在单元体上。

解：(1)MPa 6.762sin 2cos 22=--++=ατασσσσσαx yx yxM P a7.322cos 2sin 2-=+-=ατασσταx yx (2)22min max )2(2xy y x y x τσσσσσσ+-±+=98.12198.81-=MPa 98.811=σMPa ，02=σ，98.1213-=σ35.3940200arctan 21)2arctan(210==--=y x xy σστα2.解：取合适坐标轴令25=x σ MPa ，9.129-=x τ 由02cos 2sin 2120=+-=ατασστxy yx得125-=yσMPa所以22min max )2(2xy y x y x τσσσσσσ+-±+=20010015050)9.129(755022-=±-=-+±-= MPa1001=σMPa ，02=σ，2003-=σ MPa3. 一点处两个互成 45平面上的应力如图所示，其中σ未知，求该点主应力。

解：150=y σ MPa ，120-=x τ MPaMPa由 ατασστ2cos 2sin 245xy yx +-=802150-=-=x σ得 10-=x σ MPa 所以22min max )2(2xyy x y x τσσσσσσ+-±+=22.7422.214-= MPa22.2141=σ MPa ，02=σ，22.743-=σ4. 图示封闭薄壁圆筒，内径100=d mm ，壁厚2=t mm ，承受内压4=p MPa ，外力偶矩192.0=e M kN ·m 。

求靠圆筒内壁任一点处的主应力。

解：75.505.032)1.0104.0(π10192.0443=⨯-⨯=x τMPa504==t pd x σ MPa1002==tpd y σ MPa35.497.100)2(222min max =+-±+=xy y x y xτσσσσσσ MPa7.1001=σ MPa ，35.492=σ MPa ，43-=σ MPa5. 受力体某点平面上的应力如图示，求其主应力大小。

解：取坐标轴使100=x σMPa ，20=x τατασσσσσα2sin 2cos 22x yx yx --++='45-M e40120sin 20120cos 21002100=--++=yyσσ得1.43=yσMPa22min max )2(2xy y x y x τσσσσσσ+-±+=77.3633.106=MPa 33.1061=σMPa ，77.362=σMPa ，03=σ6.解：22min max )2(2xyy x y x τσσσσσσ+-±+=16.4216.5216.47540252203022-=±=+±-=所以2.521=σMPa ，102=σMPa ，16.423-=σMPa2.47231max =-=σστMPa7. 图示工字形截面梁AB ，截面的惯性矩61056.72-⨯=z I m 4，求固定端截面翼缘和腹板交界处点a 的主应力和主方向。

解：17.361056.7207.075.0105063=⨯⨯⨯⨯=-σ MPa （压应力）8.81056.7203.01085301501050693=⨯⨯⨯⨯⨯⨯⨯=--τMPa22min max )2(2xy y x y x τσσσσσσ+-±+=2.3803.2-= MPa03.21=σ MPa ，02=σ，2.383-=σ MPa05.7717.368.82arctan 21)2arctan(210=⨯-=--=y x xy σστα50kN AB0.75mσ305.77τaσaσ18. 图示矩形截面拉杆受轴向拉力F ，若截面尺寸b 、h 和材料的弹性模量E ，泊松比ν均已知，试求杆表面 45方向线段AB 的改变量=∆AB L ？ 解：bhFx=σ，0=y σ，0=xy τ bh F2=ασ，bh F 22=+απσ（ 45=α所以)1(2)22(145v EbhFbh F bh F E -=-=νεEbF Ebh Fh AB L AB 2)1(2)1(2245ννε-=-⨯==∆ 9. 一边长为50 mm 的正方形硬铝板处于纯剪切状态，若切应力80=τ MPa ，并已知材料的弹性模量72=E GPa ，泊松比34.0=ν。

试求对角线AC 的伸长量。

解：8045=σMPa ，80135-= σMPa39451048.1)8034.080(10721-⨯=⨯+⨯=ε 25=AC L00105.01048.1253=⨯⨯=∆-AC Lmm10. 一变形体A 四周和底边均与刚性边界光滑接触，上边受均布压力0σ。

已知材料的的弹性模量E ，水平方向上的应变和应力。

解：0σσ-=y，z x σσ=，0==z x εε0)]([1=+-=z y x x E σσνσε，得到10-==ννσσσz x )121()]12([1)]([12000ννσννσνσσσνσε---=---=+-=E E E z x y y11. 设地层由石灰岩组成，其密度3105.2⨯=ρ kg/m 3，泊松比2.0=ν。

计算离地面200m 深处的地压应力。

解： 9.42008.9105.23-=⨯⨯⨯-=y σ MPaz x σσ=，0==zx εε0)]9.4(2.0[1=+-⨯-=z x x Eσσε得到22.1-==zx σσ MPa12. 一体积为101010⨯⨯ mm 3的立方铝块，将其放入宽为10 mm 的刚性槽中。

已知铝的泊松比ν33.0=解： 6001.001.010633-=⨯⨯-=σMPa,01=σ由0)6033.0(122=⨯+=σεE得8.192-=σ13. 直径为D 的实心圆轴，受外力偶e M 作用如图。

测得轴表面点A 与轴线成 45方向的线应变为ε，试导出用e M 、D 、ε表示的切变弹性模量G 的表达式。

解：τσ=-45，τσ-=45τνε)1(145+=E，所以ετG 2=又316D M e πτ=，所以ED M G e 38π=14. 直径100=d mm 的圆轴，受轴向拉力F 和力偶矩e M 作用。

材料的弹性模量200=E GPa ，泊松比3.0=ν。

现测得圆轴表面200mσxσzσy的轴向线应变6010500-⨯=ε，45方向的线应变64510400-⨯=ε，求F 和e M 。

解：7850=⋅=A E F ε kN 设力偶矩引起的切应力为ττσ+=-5045，τσ-=5045)(1454545 νσσε-=-E ]10)50(3.010)50[(102001669⨯-⨯-⨯+⨯=ττ610400-⨯=6.34=τ MPa ，又3)1.0(π16⨯=M τ8.6=e MkN ·m15. 直径100=d mm 的实心钢球，受静水压力42=p MPa 作用。

求直径和体积的缩减量。

设钢球的弹性模量210=E GPa ，泊松比3.0=ν。

解：因为42321-=-===q σσσ MPa所以333211024.042310210)3.021()(21-⨯-=⨯⨯⨯⨯--=++-=σσσνθE 533211108102108.16)]([1-⨯-=⨯-=+-=σσνσεE 得23310257.1100)6(1024.0--⨯-=⨯⨯⨯-==∆πθV Vmm 3351108100108--⨯-=⨯⨯-==∆d d εmm16. 边长10=a 0 mm 的立方体，已知弹性模量200=E GPa ，泊松比3.0=ν。

如将立方体沉入100 m 深的水中，求其体积变化。

解：因为1321-=-===gh ρσσσMPa)(21321σσσνθ++-=E 63106)3(102006.01-⨯-=-⨯⨯-=61.01.01.01066-=⨯⨯⨯⨯--==∆-V V θmm 3ττ17. 图示拉杆，F ，b ，h 及材料的弹性常数E 、ν均为已知。

试求线段AB 的正应变和转角。

解：bhF x =σ，bhF 213545==σσ所以)1(2)(!13545ννσσε-=-=bhEF E AB 又因为bhE F x =ε，bhEFv y -=ε所以bhEv F bhE vF bhE F AB )1()(45+-=+-== γϕ18. 图示曲拐ABC 在水平面内，悬臂端C 处作用铅垂集中力F 。

在上表面E 处，沿与母线成 45方向贴一应变片，已测得线应变45ε，求载荷F 值。

已知长度l 、a 、直径d 及材料的常数E 、v 。

解：应力状态如图示，332d Fl πσ=，316d Fa πτ=τσσ+=245，τσσ-=-245所以)(!454545--=σσεv E所以)1(16)1(16345v a v l dE F ++-=πε19. 三个弹性常数之间的关系：)]1(2/[ν+=E G 适用于 (A)任何材料在任何变形阶段； (B)各向同性材料在任何变形阶段；(C)各向同性材料应力在比例极限范围内； (D)任何材料在弹性变形范围内。

答：C20. 一实心均质钢球，当其外表面处迅速均匀加热，则球心O 点处的应力状态。

(A)单向拉伸应力状态； (B)二向拉伸应力状态； (C)三向等值拉伸应力状态； (D)三向压缩应力状态。

答：C/2στσ/2σ21. 混凝土立方体试样作单向压缩试验时，若在其上、下压板面上涂有润滑剂，则试样破坏时将沿纵向剖面裂开的主要原因。

(A)最大压应力； (B)最大切应力； (C)最大伸长线应变； (D)存在横向拉应力。

答：C22. 已知单元体的主应力为1σ，2σ，推证两相互垂直的截面上的正应力之和为常数 。

证：ασσσσσα2cos 222121-++=)90(2cos 222121︒+-++=ασσσσσβ=+=+21σσσσβα常数 得证。

23. 受内压的薄壁圆筒，已知内压为p ，平均直径为D ，壁厚为t ，弹性常数为E 、ν。

试确定圆筒薄壁上任一点的主应力、主应变及第三、第四强度理论的相当应力。

解：tpD 21=σ，tpD 42=σ，03=σ)2(4)42(1)(1211νννσσε-=-=-=tE pD t pD t pD E E)21(4)24(1)(1122νννσσε-=-=-=tE pD t pD t pD E EtEpD t pD E E 43]430[1)](0[1213ννσσνε-=-=+-=tpD231r3=-=σσσ])()()[(21213232221r4σσσσσσσ-+-+-=t pD 43=24. 图示正方形截面棱柱体，弹性常数E 、ν均为已知。