湖南省邵阳市数学八年级上学期期末专题复习 专题3:全等三角形
- 格式:doc
- 大小:1.21 MB
- 文档页数:18
2020-2021学年湖南省八年级上册数学(人教版)期末考试复习:第12章《全等三角形》解答题精选一.解答题(共25小题)1.(2020春•邵阳县期末)如图,AC平分∠BAD,CE⊥AB,CD⊥AD,点E、D为垂足,CF=CB.(1)求证:BE=FD;(2)若AC=10,AD=8,求四边形ABCF的面积.2.(2020春•澧县期末)如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.(1)Rt△ADE与Rt△BEC全等吗?并说明理由;(2)若DE=2,求DC的长.3.(2020春•岳阳期末)如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,且E为AB的中点.(1)求∠B的度数.(2)若DE=5,求BC的长.4.(2020春•长沙期末)如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F.DF的延长线交AC于点G.(1)若∠B=40°.求∠ADF的度数;(2)求证:FG=FE.5.(2020春•长沙期末)如图,在△ACD中,E为边CD上一点,F为AD的中点,过点A作AB∥CD,交EF的延长线于点B.(1)求证:△AFB≌△DFE;(2)若AB=6,DC=4CE,求CD的长.6.(2020春•开福区校级期末)如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,(1)求证:AD平分∠BAC;(2)已知AC=16,DE=4,求△ADC的面积.7.(2020春•天心区期末)如图,点A,B,C,D在同一直线上,AE∥DF,CE∥BF,AE=FD.求证:AB =CD.下面是推理过程,请将下列过程填写完整:证明:∵AE∥DF,∴∠A=∠D,().∵CE∥BF,∴∠ECA=∠FBD,又∵AE=DF,∴△AEC≌△DFB(),∴AC=DB,∴AC﹣=DB﹣,()∴AB=CD.8.(2020春•雨花区期末)如图,已知AB⊥CF于点B,DE⊥CF于点E,BH=EG,AH=DG,∠C=∠F.(1)求证:△ABH≌△DEG;(2)求证:CE=FB.9.(2020春•永州期末)如图,D为BC的中点,DE⊥AB于点E,DF⊥AC于点F,且DE=DF.试问:AB 与AC有什么关系?10.(2019秋•浏阳市期末)如图,AB=DE,AC=DF,BE=CF.求证:∠A=∠EGC=∠D.11.(2019秋•涟源市期末)如图,在△ABC中,∠BAC=90°,E为边BC上的任意点,D为线段BE的中点,AB=AE,EF⊥AE,AF∥BC.(1)求证:∠DAE=∠C;(2)求证:AF=BC.12.(2019秋•郴州期末)如图,点C、F在BE上,BF=EC,AB∥DE,且∠A=∠D,求证:AC=DF.13.(2019秋•慈利县期末)如图(1),AB=7cm,AC⊥AB,BD⊥AB垂足分别为A、B,AC=5cm.点P 在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动.它们运动的时间为t (s)(当点P运动结束时,点Q运动随之结束).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,并判断此时线段PC和线段PQ的位置关系,请分别说明理由;(2)如图(2),若“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,点Q的运动速度为xcm/s,其他条件不变,当点P、Q运动到某处时,有△ACP与△BPQ全等,求出相应的x、t的值.14.(2020春•岳麓区校级期末)如图,已知点A,C,D在同一直线上,BC与AF交于点E,AF=AC,AB =DF,AD=BC.(1)求证:∠ACE=∠EAC;(2)若∠B=50°,∠F=110°,求∠BCD的度数.15.(2020春•新邵县期末)如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;求证:CF=EB.16.(2019秋•耒阳市期末)如图:已知AB=AD,BC=DC,求证:∠B=∠D.17.(2019秋•娄底期末)已知:如图,点E,C在线段BF上,AC=DF,AC∥DF,BE=CF.求证:AB∥DE.18.(2020春•渌口区期末)如图,BD,CE分别是△ABC的高,且BE=CD,求证:Rt△BEC≌Rt△CDB.19.(2019秋•娄底期末)如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P 在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP 全等?20.(2019秋•永州期末)证明题:如图,在△ABC中,AB=AC,CD⊥AB于点D,BE⊥AC于点E,求证:CD=BE.21.(2019秋•慈利县期末)雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE=13AB,AF=13AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.22.(2019春•靖州县期末)如图,在Rt△ABC中,∠C=90°,E是AB上的点,且AE=AC,DE⊥AB交BC于D,AC=6,BC=8,CD=3.(1)求DE的长;(2)求△ADB的面积.23.(2018秋•安化县期末)如图,已知∠1=∠2,∠A=∠D,求证:CA=CD.24.(2019春•雨花区校级期末)如图,四边形ABCD中,AB=BC=2CD,AB∥CD,∠C=90°,E是BC 的中点,AE与BD相交于点F,连接DE(1)求证:△ABE≌△BCD;(2)判断线段AE与BD的数量关系及位置关系,并说明理由;(3)若CD=1,试求△AED的面积.25.(2019春•醴陵市期末)如图,在四边形ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于点E,AF⊥CD交CD的延长线于点F.求证:△ABE≌△ADF.2020-2021学年湖南省八年级上册数学(人教版)期末考试复习:第12章《全等三角形》解答题精选参考答案与试题解析一.解答题(共25小题)1.【解答】(1)证明:∵AC平分∠BAD,CE⊥AB,CD⊥AD,∴CD=CE,在Rt△CBE和Rt△CFD中,{CC=CCCC=CC,∴Rt△CBE≌Rt△CFD(HL),∴BE=FD;(2)解:在Rt△ACD中,∵AC=10,AD=8,∴CD=√102−82=6,∵AC=AC,CD=CE,∴Rt△ACD≌Rt△ACE(HL),∴S△ACD=S△ACE,∵Rt△CBE≌Rt△CFD,∴S△CBE=S△CFD,∴四边形ABCF的面积=S四边形AECD=2S△ACD=2×12×6×8=48.2.【解答】解:(1)结论:Rt△ADE≌Rt△BEC;理由如下:∵∠1=∠2,∴DE=CE,而∠A=∠B=90°,AE=BC∴在Rt△ADE和Rt△BEC中,{CC=CCCC=CC∴Rt△ADE≌Rt△BEC(HL);(2)∵Rt△ADE≌Rt△BEC,∴∠AED=∠BCE,∠ADE=∠BEC,又∵∠AED+∠ADE=90°,∠BEC+∠BCE=90°,∴2(∠AED+∠BEC)=180°,∴∠AED+∠BEC=90°,∴∠DEC=90°,∵DE=EC,DE=2,∴CD=√2DE=2√2.3.【解答】解:(1)∵DE⊥AB于点E,E为AB的中点,∴DE是线段AB的垂直平分线,∴DA=DB,∴∠2=∠B,∵∠C=90°,∴∠B=∠1=∠2=30°;(2)∵DE⊥AB,∠B=30°,∴BD=2DE=10,∵AD平分∠CAB,∠C=90°,DE⊥AB,∴DC=DE=5,∴BC=CD+BD=15.4.【解答】解:(1)∵AF平分∠CAB,∴∠CAF=∠DAF.在△ACF和△ADF中,∵{CC=CCCCCC=CCCC CC=CC,∴△ACF≌△ADF(SAS).∴∠ACF=∠ADF.∵∠ACB=90°,CE⊥AB,∴∠ACE+∠CAE=90°,∠CAE+∠B=90°,∴∠ACF=∠B,∴∠ADF=∠B=40°.②证明:∵∠ADF=∠B,∴DF ∥BC ,∵BC ⊥AC ,∴FG ⊥AC .∵FE ⊥AB ,又AF 平分∠CAB ,∴FG =FE .5.【解答】(1)证明:∵AB ∥CD , ∴∠ABF =∠DEF ,∠BAF =∠D , ∵F 为AD 的中点,∴AF =DF ,在△AFB 和△DFE 中,{∠CCC =∠CCCCCCC =CC CC =CC,∴△AFB ≌△DFE (AAS ),(2)∵△AFB ≌△DFE ,∴AB =DE =6,∵DC =4CE ,∴CE +6=4CE ,∴CE =2.∴CD =CE +DE =2+6=8.6.【解答】(1)证明:∵DE ⊥AB ,DF ⊥AC , ∴∠E =∠DFC =90°,在Rt △BED 和Rt △CFD 中{CC =CCCC =CC∴Rt △BED ≌Rt △CFD (HL ),∴DE =DF ,∵DE ⊥AB ,DF ⊥AC ,∴AD 平分∠BAC ;(2)解:∵DE =DF ,DE =4,∴DF =4,∵AC =16,∴△ADC 的面积是12×CC ×CC =12×16×4=32.7.【解答】证明:∵AE ∥DF ,∴∠A =∠D (两直线平行,内错角相等),∵CE ∥BF ,∴∠ECA =∠FBD ,在△AEC 和△DFB 中{∠CCC =∠CCC CC =CCCC =CC∴△AEC ≌△DFB (AAS ),∴AC =DB ,∴AC ﹣BC =DB ﹣BC (等式的性质),∴AB =CD ,故答案为:两直线平行,内错角相等,AAS ,BC ,BC ,等式的性质.8.【解答】(1)证明:∵AB ⊥CF ,DE ⊥CF ,∴∠DEG =∠ABH =90°,在Rt △ABH 和Rt △DEG 中,∵{CC =CC CC =CC, ∴Rt △ABH ≌Rt △DEG (HL ).(2)∵Rt △ABH ≌Rt △DEG (HL ).∴AB =DE ,在△ABC 和△DEF 中,∵{∠CCC =∠CCC =90°CC =CCCC =CC ,∴△ABC ≌△DEF (AAS ).∴BC =EF ,∴CE =FB .9.【解答】解:AB 与AC 相等,∵D 为BC 的中点,∴BD =CD ,∵DE ⊥AB 于点E ,DF ⊥AC 于点F ,∴∠BED =∠CFD =90°∵在Rt △BED 和Rt △CFD 中,{CC =CC CC =CC∴Rt △BED ≌Rt △CFD (HL )∴∠B =∠C ,∴AB =AC .10.【解答】证明:如图,∵BE =CF ,∴BC =EF ,在△ABC 和△DEF 中,{CC =CC CC =CC CC =CC,∴△ABC ≌△DEF (SSS ).∴∠A =∠D ,∠B =∠DEF .∴AB ∥DE ,∴∠A =∠EGC ,∴∠A =∠EGC =∠D .11.【解答】证明:(1)∵AB =AE ,D 为线段BE 的中点,∴AD ⊥BC ,(三线合一没有学习到,可以用全等证明)∴∠C +∠DAC =90°,∵∠BAC =90°∴∠BAD +∠DAC =90°∴∠C =∠BAD ,∵AB =AE ,AD ⊥BE ,∴∠BAD =∠DAE ,∴∠DAE =∠C(2)∵AF ∥BC∴∠F AE =∠AEB∵AB =AE∴∠B =∠AEB∴∠B =∠F AE ,且∠AEF =∠BAC =90°,AB =AE∴△ABC ≌△EAF (ASA )∴AC =EF12.【解答】证明:∵BF =EC (已知),即BC +CF =EF +FC ,∴BC =EF (等式性质).∵AB ∥DE ,∴∠B =∠E (两直线平行,内错角相等).在△ABC 和△DEF 中{∠C =∠CCC =CC CC =CC,∴△ABC ≌△DEF (AAS ).∴AC =DF (全等三角形对应边相等).13.【解答】解:(1)△ACP ≌△BPQ ,∵AC ⊥AB ,BD ⊥AB∴∠A =∠B =90°∵AP =BQ =2,∴BP =5,∴BP =AC ,在△ACP和△BPQ中,{CC=CC CC=CC CC=CC,∴△ACP≌△BPQ;∴∠C=∠BPQ,∵∠C+∠APC=90°,∴∠APC+∠BPQ=90°,∴∠CPQ=90°,∴PC⊥PQ;(2)存在x的值,使得△ACP与△BPQ全等,②若△ACP≌△BPQ,则AC=BP,AP=BQ,可得:5=7﹣2t,2t=xt 解得:x=2,t=1;②若△ACP≌△BQP,则AC=BQ,AP=BP,可得:5=xt,2t=7﹣2t解得:x=207,t=74.14.【解答】(1)证明:在△ABC和△FDA中,∵AB=FD,AC=F A,BC=DA,∴△ABC≌△FDA(SSS),∴∠ACE=∠EAC.(2)解∵△ABC≌△FDA,∠F=110°,∴∠BAC=∠F=110°,又∵∠BCD是△ABC的外角,∠B=50°,∴∠BCD=∠B+∠BAC=160°.15.【解答】证明:∵∠C=90°,∴DC⊥AC.∵AD 是∠BAC 的平分线,DE ⊥AB ,∴DC =DE .在Rt △DCF 和Rt △DEB 中,{CC =CC CC =CC, ∴Rt △DCF ≌Rt △DEB (HL ),∴CF =EB .16.【解答】证明:连接AC .在△ACB 和△ACD 中,{CC =CC CC =CC CC =CC,∴△ACB ≌△ACD (SSS ),∴∠B =∠D .17.【解答】证明:∵AC ∥DF ,∴∠ACB =∠DFE .又∵BE =CF ,∴BC =EF .在△ABC 和△DEF 中,{CC =CC CCCC =CCCC CC =CC∴△ABC ≌△DEF (SAS ).∴∠ABC =∠DEF ,∴AB ∥DE .18.【解答】证明:∵BD ,CE 分别是△ABC 的高,∴∠BEC =∠CDB =90°,在Rt △BEC 和Rt △CDB 中,{CC =CC CC =CC, ∴Rt △BEC ≌Rt △CDB (HL ).19.【解答】解:(1)经过1秒后,PB =3cm ,PC =5cm ,CQ =3cm ,∵△ABC 中,AB =AC ,∴在△BPD 和△CQP 中,{CC =CC CCCC =CCCC CC =CC,∴△BPD ≌△CQP (SAS ).(2)设点Q 的运动速度为x (x ≠3)cm /s ,经过ts △BPD 与△CQP 全等;则可知PB =3tcm ,PC =8﹣3tcm ,CQ =xtcm ,∵AB =AC ,∴∠B =∠C ,根据全等三角形的判定定理SAS 可知,有两种情况:②当BD =PC ,BP =CQ 时,②当BD =CQ ,BP =PC 时,两三角形全等;②当BD =PC 且BP =CQ 时,8﹣3t =5且3t =xt ,解得x =3,∵x ≠3,∴舍去此情况;②BD =CQ ,BP =PC 时,5=xt 且3t =8﹣3t ,解得:x =154; 故若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为154cm /s 时,能够使△BPD 与△CQP全等.20.【解答】证明:∵CD ⊥AB 于点D ,BE ⊥AC ,∴∠AEB =∠ADC =90°,又∠A =∠A ,AB =AC ,∴△ABE ≌△ACD (AAS ).∴CD =BE .21.【解答】解:雨伞开闭过程中二者关系始终是:∠BAD =∠CAD ,理由如下:∵AB =AC ,AE =13AB ,AF =13AC ,∴AE =AF ,在△AOE 与△AOF 中,{CC =CC CC =CC CC =CC,∴△AOE ≌△AOF (SSS ),∴∠BAD =∠CAD .22.【解答】解:(1)∵∠C =90°,DE ⊥AB ,∴∠C =∠AED =90°,在Rt △ACD 和Rt △AED 中,{CC =CCCC =CC ,∴Rt △ACD ≌Rt △AED (HL ),∴CD =DE =3;(2)∵∠C =90°,AC =6,BC =8,∴AB √CC 2+CC 2=10,∵DE =3,∴△ADB 的面积=12×10×3=15.23.【解答】证明:∵∠1=∠2,∴∠ACB =∠DCB .在△ABC 与△DBC 中,{∠C =∠CCCCC =CCCC CC =CC,∴△ABC ≌△DBC (AAS ),∴CA =CD .24.【解答】(1)证明:∵AB ∥CD ,∴∠ABE +∠C =180°,∵∠C =90°,∴∠ABE =90°=∠C ,∵E 是BC 的中点,∴BC =2BE ,∵BC =2CD ,∴BE=CD,在△ABE和△BCD中,{CC=CCCCCC=CCCC=CC,∴△ABE≌△BCD(SAS);(2)解:AE=BD,AE⊥BD,理由如下:由(1)得:△ABE≌△BCD,∴AE=BD,∵∠BAE=∠CBD,∠ABF+∠CBD=90°,∴∠ABF+∠BAE=90°,∴∠AFB=90°,∴AE⊥BD;(3)解:∵△ABE≌△BCD,∴BE=CD=1,∵AB=BC=2CD=2,∴CE=BC﹣BE=1,∴CE=CD,∴△AED的面积=梯形ABCD的面积﹣△ABE的面积﹣△CDE的面积=12(1+2)×2−12×2×1−12×1×1=32.25.【解答】证明:∵CA平分∠BCD,AE⊥BC于点E,AF⊥CD交CD的延长线于点F,∴AE=AF.在Rt△ABE与Rt△ADF中,{CC=CCCC=CC,∴Rt△ABE≌Rt△ADF(HL).。

《三角形全等的判定》知识全解课标要求1.探索几何的基本图形——三角形,探索全等三角形的基本性质、三角形全等的判定条件和其相互关系,及角平分线性质,进一步丰富对空间图形的认识和感受.2.在探索全等三角形的性质、与他人合作交流等活动过程中,发展合情合理,进一步学习有条理地思考与表达;在积累了三角形的性质的基础上,探索全等三角形的判定条件和角平分线性质及其逆运用.知识结构内容解析在一个三角形的三条边,三个角中任取三个元素,可以有下列组合;SAS、SSA、ASA、AAS、SSS、AAA,但其中SSA和AAA不能判定三角形全等。
◆如何选择三角形证全等(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等。
(2)可以从已知条件出发,看已知条件确定哪两个三角形可证它们全等;(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;(4)如果以上方法都行不通,可采用添加辅助线的方法,构造三角形全等。
重点难点本节的重点是:掌握三角形全等的判定定理,并灵活运用。
本节的难点是:在较复杂的图形中,找出证明两个三角形全等的条件,恰当的选择判定定理,正确地书写演绎推理过程。
教法导引1.注重培养探索归纳能力经历探究三角形全等条件的过程:由全等三角形的定义可以知道,由三条边对应相等、三个角对应相等能判定三角形全等,那么减少条件能否判定三角形全等呢?于是,依次探究:满足一个条件、两个条件、三个条件、……能否判定三角形全等.通过探究得到:满足一个条件、两个条件不能判定三角形全等;满足三个条件不一定能判定三角形全等,即“边边边”、“边角边”、“角边角”、“角角边”能判定三角形全等,“边边角”、“角角角”不能判定三角形全等.将三角形全等的判定方法运用于直角三角形,可以判定直角三角形全等;但对于满足斜边和直角边对应相等的两个直角三角形,就无法运用三角形全等的判定方法来进行判断了,因此应探究“斜边、直角边”能否判定直角三角形全等.2.注重培养推理能力本章要求学生有理有据地推理论证,精炼准确地表达推理过程,这对于学生比较困难,因此我们在教学中应采取以下措施突破难点:(1)注意减缓坡度,循序渐进.精心选择全等三角形的证明问题,开始阶段的例题,证明方向明确、过程简单,容易规范书写格式,主要让学生体会证明思路及格式.然后逐步增加题目的复杂程度,每一步都为下一步做准备,下一步又要注意复习前一步训练过的内容.(2)在不同的阶段,安排不同的内容,突出一个重点.先安排证明两个三角形全等,进而安排通过证明三角形全等证明两条线段或两个角相等,重点使学生熟悉证明的步骤和方法.最后安排的问题涉及前面学过的内容,重点培养学生分析问题,选择推理途径的证明能力.(3)注重分析思路注重分析思路,让学生学会思考问题.(4)注重规范书写格式注重规范书写格式,让学生学会清楚地表达思考的过程.3.注重联系实际从实际例子引入全等形的概念,易于学生理解概念,易于调动学生学习的积极性.从分析平分角仪器的原理引入角平分线的画法,通过确定集贸市场位置的问题引出“角的内部到角的两边的距离相等的点在角的平分线上”的结论,使学生感受理论来源于实际的需要.运用全等三角形可以解决实际中许多测量边、角的问题.学法建议学生在初一学习过三角形的相关知识,会作一个三角形等于已知三角形,本节是使学生在原有知识的基础上探索怎样判定三角形全等的判定条件及恰当地选择判定定理来判别两个三角形全等,并能灵活运用全等三角形的判定方法解决线段或者角相等的问题。


全等三角形八年级上册数学期末知识点复习
全等三角形八年级上册数学期末知识点复习
一、全等图形、全等三角形:
1.全等图形:能够完全重合的两个图形就是全等图形。
2.全等图形的性质:全等多边形的对应边、对应角分别相等。
3.全等三角形:三角形是特殊的多边形,因此,全等三角形的对应边、对应角分别相等。
同样,如果两个三角形的边、角分别对应相等,那么这两个三角形全等。
说明:全等三角形对应边上的高,中线相等,对应角的平分线相等;全等三角形的`周长,面积也都相等。
这里要注意:(1)周长相等的两个三角形,不一定全等;(2)面积相等的两个三角形,也不一定全等。
二、全等三角形的判定:
1.一般三角形全等的判定
(1)边边边公理:三边对应相等的两个三角形全等(“边边边”或“SSS”)。
(2)边角公理:两边和它们的夹角对应相等的两个三角形全等(“边角边”或“SAS”)。
(3)角边角公理:两个角和它们的夹边分别对应相等的两个三角形全等(“角边角”或“ASA”)。
(4)角角边定理:有两角和其中一角的对边对应相等的两个三角形全等(“角角边”或“AAS”)。
2.直角三角形全等的判定
利用一般三角形全等的判定都能证明直角三角形全等.
斜边和一条直角边对应相等的两个直角三角形全等(“斜边、直角边”或“HL”).
注意:两边一对角(SSA)和三角(AAA)对应相等的两个三角形不一定全等。
三、角平分线的性质及判定:
性质定理:角平分线上的点到该角两边的距离相等。
判定定理:到角的两边距离相等的点在该角的角平分线上。


2020-2021学年湖南省八年级上册数学(人教版)期末考试复习:第12章《全等三角形》选择题精选一.选择题(共35小题)1.(2020春•邵阳县期末)如图,OD平分∠AOB,DE⊥AO于点E,DE=4,点F是射线OB上的任意一点,则DF的长度不可能是()A.3 B.4 C.5 D.62.(2020春•桃江县期末)下列条件中,不能判定△ABC与△DEF一定全等的是()A.AB=DE,BC=EF,∠A=∠D=90°B.AB=DE,BC=EF,∠A=∠D=80°C.AB=DE,∠A=∠D=90°,∠B=∠E=40°D.BC=EF,∠A=∠D=80°,∠B=∠E=40°3.(2020春•开福区校级期末)如图,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD 于点G,则下列结论:①DF+AE>AD;②DE=DF;③AD⊥EF;④S△ABD:S△ACD=AB:AC,其中正确结论的个数是()A.1个B.2个C.3 个D.4个4.(2020春•雨花区期末)如图,已知△ABD≌△ACE,下列说法错误的是()A.∠B=∠C B.EB=DC C.AD=DC D.△EFB≌△DFC5.(2020春•雨花区校级期末)下列条件中能判定△ABC≌△DEF的是()A.AB=DE,BC=EF,∠A=∠D B.∠A=∠D,∠B=∠E,∠C=∠FC.AC=DF,AB=DE D.∠B=∠E,∠C=∠F,AC=DF6.(2019秋•浏阳市期末)若△ABC≌△DEF,则根据图中提供的信息,可得出x的值为()A.30 B.27 C.35 D.407.(2019秋•耒阳市期末)如图,AB=DE,∠A=∠D,添加以下条件,不能使△ABC≌△DEF的是()A.AC=DF B.BC=EF C.∠B=∠E D.∠C=∠F8.(2019秋•慈利县期末)如图,小周书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他的依据是()A.SAS B.ASA C.SSS D.AAS9.(2020春•开福区校级期末)如图,已知CD=CA,∠D=∠A,添加下列条件中的()仍不能证明△ABC≌△DEC.A.DE=AB B.CE=CB C.∠DEC=∠B D.∠ECD=∠BCA10.(2020春•天心区期末)对于任意△ABC(见示意图).若AD是△ABC的边BC上的中线,∠ADB、∠ADC的角平分线分别交AB、AC于点E、F,连接EF,那么EF、BE、CF之间的数量关系正确的是()A.BE+CF>EF B.BE+CF≥EF C.BE+CF<EF D.BE+CF=EF11.(2020春•天心区期末)如图,△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC =8,DE=3,则△BCE的面积等于()A.11 B.8 C.12 D.312.(2019秋•新化县期末)如图,在△ABC中,AB=6,BC=5,AC=4,AD平分∠BAC交BC于点D,在AB上截取AE=AC,则△BDE的周长为()A.8 B.7 C.6 D.513.(2019秋•新化县期末)如图,AB=AC,AE=AD,要使△ACD≌△ABE,需要补充的一个条件是()A.∠B=∠C B.∠D=∠E C.∠BAC=∠EAD D.∠B=∠E14.(2019秋•娄底期末)工人师傅经常利用角尺平分一个任意角,如图所示,∠AOB是一个任意角,在边OA,OB上分别取OD=OE,移动角尺,使角尺两边相同的刻度分别与D,E重合,这时过角尺顶点P的射线OP就是∠AOB的平分线.你认为工人师傅在此过程中用到的三角形全等的判定方法是这种作法的道理是()A.SAS B.ASA C.AAS D.SSS15.(2020春•岳阳期末)如图所示,∠C=∠D=90°添加一个条件,可使用“HL”判定Rt△ABC与Rt △ABD全等.以下给出的条件适合的是()A.AC=AD B.AB=AB C.∠ABC=∠ABD D.∠BAC=∠BAD16.(2018秋•炎陵县期末)如图,阿牛不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),他认为只须将其中的第2块带去,就能配一块与原来一样大小的三角形,阿牛这样做的理由是()A.SAS B.ASA C.AAS D.SSS17.(2019春•雨花区校级期末)如图,在△ABC中,∠A=50°,∠B=∠C,点D,E,F分别在边BC,CA,AB上,且满足BF=CD,BD=CE,∠BFD=30°,则∠FDE的度数为()A.75°B.80°C.65°D.95°18.(2018秋•雨花区期末)如图,点B、E,C,F在同一条直线上,AB=DE,要使△ABC≌△DEF,则需要再添加的一组条件不可以是()A.∠A=∠D,∠B=∠DEF B.BC=EF,AC=DFC.AB⊥AC,DE⊥DF D.BE=CF,∠B=∠DEF19.(2019春•赫山区期末)如图,OC为∠AOB的平分线,CM⊥OB于M,OC=5,OM=4,则点C到射线OA的距离为()A.2 B.3 C.4 D.520.(2018秋•南县期末)如图,给出的四组条件中,不能证明△ABC≌△DEF的是()A.AB=DE,BC=EF,AC=DF B.AB=DE,∠B=∠E,BC=EFC.AB=DE,AC=DF,∠B=∠E D.∠B=∠E,BC=EF,∠C=∠F.21.(2018秋•邵阳县期末)如图,已知AB=AC,BD=CD,E是AD上的一点,则下列结论中不成立的是()A.∠BAD=∠CAD B.∠BED=∠CED C.BE=CE D.AE=DE22.(2018秋•冷水江市期末)如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是()A.∠M=∠N B.AB=CD C.AM=CN D.AM∥CN23.(2018秋•冷水江市期末)下列叙述中:①任意一个三角形的三条高至少有一条在此三角形内部;②以a,b,c为边(a,b,c都大于0,且a+b>c)可以构成一个三角形;③一个三角形内角之比为3:2:1,此三角形为直角三角形;④有两个角和一条边对应相等的两个三角形全等;正确的有()个.A.1 B.2 C.3 D.424.(2018秋•古丈县期末)如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于()A.5 B.7 C.10 D.325.(2018秋•永定区期末)已知:如图,AB=AD,∠1=∠2,以下条件中,不能推出△ABC≌△ADE的是()A.AE=AC B.∠B=∠D C.BC=DE D.∠C=∠E26.(2018秋•凤凰县期末)下列说法正确的是()A.所有的等边三角形都是全等三角形B.全等三角形是指面积相等的三角形C.周长相等的三角形是全等三角形D.全等三角形是指形状相同大小相等的三角形27.(2018秋•武冈市期末)如图,已知AB=AD给出下列条件:(1)CB=CD(2)∠BAC=∠DAC(3)∠BCA=∠DCA(4)∠B=∠D,若再添一个条件后,能使△ABC≌△ADC的共有()A.1个B.2个C.3个D.4个28.(2019春•桑植县期末)下列命题中:①两直角边对应相等的两个直角三角形全等;②两锐角对应相等的两个直角三角形全等;③斜边和一直角边对应相等的两个直角三角形全等;④一锐角和斜边对应相等的两个直角三角形全等;⑤一锐角和一边对应相等的两个直角三角形全等.其中正确的个数有()A.2个B.3个C.4个D.5个29.(2018秋•永定区期末)如图,△ABC中,AD⊥BC,D为BC的中点,以下结论:(1)△ABD≌△ACD;(2)AB=AC;(3)∠B=∠C;(4)AD是△ABC的一条角平分线.其中正确的有()A.1个B.2个C.3个D.4个30.(2018春•长沙期末)如图,已知OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OBC=()A.95°B.120°C.50°D.105°31.(2018春•岳麓区校级期末)若△ABC≌△DEF,∠A=60°,∠B=50°,那么∠F的度数是()A.120°B.80°C.70°D.60°32.(2018春•涟源市期末)如图所示,在Rt△ACB中,∠C=90°,AD平分∠BAC,若CD=6,则点D 到AB的距离是()A.9 B.8 C.7 D.633.(2018春•娄星区期末)如图,PD⊥AB,PE⊥AC,垂足分别为D、E,且PD=PE,则△APD与△APE 全等的理由是()A.SAS B.AAA C.SSS D.HL34.(2017秋•开福区校级期末)如图,△ABC≌△EFD,且AB=EF,EC=4,CD=3,则AC=()A.3 B.4 C.7 D.835.(2017秋•新化县期末)四位同学做“读语句画图”练习.甲同学读语句“直线经过A,B,C三点,且点C在点A与点B之间”,画出图形(1);乙同学读语句“两条线段AB,CD相交于点P”画出图形(2);丙同学读语句“点P在直线l上,点Q在直线l外”画出图形(3);丁同学读语句“点M在线段AB的延长线上,点N在线段AB的反向延长线上”画出图形(4).其中画的不正确的是()A.甲同学B.乙同学C.丙同学D.丁同学2020-2021学年湖南省八年级上册数学(人教版)期末考试复习:第12章《全等三角形》选择题精选参考答案与试题解析一.选择题(共35小题)1.【解答】解:过D点作DH⊥OB于H,如图,∵OD平分∠AOB,DE⊥AO,DH⊥OB于H,∴DH=DE=4,∴DF≥4.故选:A.2.【解答】解:A、∵AB=DE,BC=EF,∠A=∠D=90°,∴根据HL证明Rt△ABC≌Rt△DEF,不符合题意;B、∵AB=DE,BC=EF,∠A=∠D=80°,根据ASS不能推出△ABC≌△DEF,故本选项符合题意;C、∵AB=DE,∠A=∠D=90°,∠B=∠E=40°,∴利用ASA能推出△ABC≌△DEF,故本选项不符合题意;D、∵BC=EF,∠A=∠D=80°,∠B=∠E=40°,∴利用AAS能推出△ABC≌△DEF,故本选项不符合题意;故选:B.3.【解答】解:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,∴∠AED=∠AFD=90°,DE=DF,故②正确;在Rt△AED和Rt△AFD中,∴Rt△AED≌Rt△AFD(HL),∴AE=AF,∵AD平分∠BAC,∴AD⊥EF,故③正确;∵在△AFD中,AF+DF>AD,又∵AE=AF,∴AE+DF>AD,故①正确;∵S△ABD,S△ACD,DE=DF,∴S△ABD:S△ACD=AB:AC,故④正确;即正确的个数是4个,故选:D.4.【解答】解:∵△ABD≌△ACE,∴∠B=∠C,AB=AC,AE=AD,∴AB﹣AE=AC﹣AD,∴BE=CD,在△EFB和△DFC中∴△EFB≌△DFC(AAS),无法证得AD=DC,∴正确的说法是A、B、D,错误的说法是C.故选:C.5.【解答】解:A、条件AB=DE,BC=EF,∠A=∠D不符合SAS,故A错误;B、条件∠A=∠D,∠C=∠F,∠B=∠E不符合AAS或ASA,故B错误;C、条件AC=DF,AB=DE不符合SAS或SSS,故C错误;D、条件∠B=∠E,∠C=∠F,AC=DF符合AAS的判定方法,故D正确.故选:D.6.【解答】解:∵△ABC≌△DEF,∴BC=EF=30,故选:A.7.【解答】解:∵AB=DE,∠A=∠D,∴当添加∠B=∠E时,可根据“ASA”判断△ABC≌△DEF;当添加∠C=∠F时,可根据“AAS”判断△ABC≌△DEF;当添加AC=DF时,可根据“SAS”判断△ABC≌△DEF.故选:B.8.【解答】解:小周书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是:两角及其夹边分别相等的两个三角形全等(ASA).故选:B.9.【解答】解:A.当DE=AB,CD=CA,∠D=∠A时,可得△ABC≌△DEC(SAS).B.当CE=CB,CD=CA,∠D=∠A时,不能得到△ABC≌△DEC.C.当∠DEC=∠B,CD=CA,∠D=∠A时,可得△ABC≌△DEC(AAS).D.当∠ECD=∠BCA,CD=CA,∠D=∠A时,可得△ABC≌△DEC(ASA).故选:B.10.【解答】证明:延长ED到H,使DE=DH,连接CH,FH,∵AD是△ABC的中线,∴BD=DC,∵DE、DF分别为∠ADB和∠ADC的平分线,∴∠1=∠4∠ADB,∠3=∠5∠ADC,∴∠1+∠3=∠4+∠5∠ADB∠ADC180°=90°,∵∠1=∠2,∴∠3+∠2=90°,即∠EDF=∠FDH,在△EFD和△HFD中,,∴△EFD≌△HFD(SAS),∴EF=FH,在△BDE和△CDH中,,∴△BDE≌△CDH(SAS),∴BE=CH,在△CFH中,由三角形三边关系定理得:CF+CH>FH,∵CH=BE,FH=EF,∴BE+CF>EF.故选:A.11.【解答】解:过E作EF⊥BC于F,∵CD是AB边上的高线,BE平分∠ABC,DE=3,∴EF=DE=3,∴△BCE的面积S,故选:C.12.【解答】解:∵AD是∠BAC的平分线,∴∠EAD=∠CAD在△ADE和△ADC中,,∴△ADE≌△ADC(SAS),∴ED=CD,∴BC=BD+CD=DE+BD=5,∴△BDE的周长=BE+BD+ED=(6﹣4)+5=7.故选:B.13.【解答】解:∠BAC=∠EAD,理由是:∵∠BAC=∠EAD,∴∠BAC+∠CAE=∠EAD+∠CAE,∴∠BAE=∠CAD,在△ACD和△ABE中,,∴△ACD≌△ABE(SAS),选项A、选项B,选项D的条件都不能推出△ACD≌△ABE,只有选项C的条件能推出△ACD≌△ABE,故选:C.14.【解答】解:依题意知,在△DOF与△EOF中,,∴△DOF≌△EOF(SSS),∴∠AOF=∠BOF,即OF即是∠AOB的平分线.故选:D.15.【解答】解:需要添加的条件为BC=BD或AC=AD,理由为:若添加的条件为BC=BD,在Rt△ABC与Rt△ABD中,∵,∴Rt△ABC≌Rt△ABD(HL);若添加的条件为AC=AD,在Rt△ABC与Rt△ABD中,∵,∴Rt△ABC≌Rt△ABD(HL).故选:A.16.【解答】解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,只有第2块有完整的两角及夹边,符合ASA.故选:B.17.【解答】解:∵∠B=∠C,∠A=50°∴∠B=∠C(180°﹣50°)=65°,∵∠BFD=30°,∠BFD+∠B+∠FDB=180°∴∠FDB=85°在△BDF和△CED中,,∴△BDF≌△CED(SAS),∴∠BFD=∠CDE=30°,又∵∠FDE+∠FDB+∠CDE=180°,∴∠FDE=180°﹣30°﹣85°=65°.故选:C.18.【解答】解:A、可用ASA判定两个三角形全等;B、根据SSS能判定两个三角形全等;C、无法判定两个三角形全等;D、根据SAS可以证明三角形全等.故选:C.19.【解答】解:如图,过C作CF⊥AO于F,∵OC为∠AOB的平分线,CM⊥OB,∴CM=CF,∵OC=5,OM=4,∴CM=3,∴CF=3,故选:B.20.【解答】解:A、由全等三角形的判定定理SSS能证明△ABC≌DEF,故此选项错误;B、由全等三角形的判定定理SAS能证明△ABC≌DEF,故此选项错误;C、由SSA不能证明△ABC≌DEF,故此选项正确;D、由全等三角形的判定定理ASA能证明△ABC≌DEF,故此选项错误;故选:C.21.【解答】解:在△ADB和△ADC中,,∴△ADB≌△ADC,∴∠BAD=∠CAD,∠BDE=∠CDE,在△EDC和△EDB中,,∴△EDC≌△EDB,∴BE=EC,∠BED=∠CED,故A、B、C正确,故选:D.22.【解答】解:A、∠M=∠N,符合ASA,能判定△ABM≌△CDN,故A选项不符合题意;B、AB=CD,符合SAS,能判定△ABM≌△CDN,故B选项不符合题意;C、根据条件AM=CN,MB=ND,∠MBA=∠NDC,不能判定△ABM≌△CDN,故C选项符合题意;D、AM∥CN,得出∠MAB=∠NCD,符合AAS,能判定△ABM≌△CDN,故D选项不符合题意.故选:C.23.【解答】解:∵锐角三角形的三条高都在三角形的内部,直角三角形有一条高在三角形的内部,两条在三角形的两边上,钝角三角形的一条高在三角形的内部,两条高在三角形的外部,∴①正确;∵当a=2,b=c=1时,满足a+b>c,但是边长为1、1、2不能组成三角形,∴②错误;∵设三角形的三角为3x°,2x°,x°,∴由三角形的内角和定理得:3x+2x+x=180,∴x=30,3x=90,即三角形是直角三角形,∴③正确;∵有两个角和一条边对应相等的两个三角形全等,∴④正确;故选:C.24.【解答】解:作EF⊥BC于F,∵BE平分∠ABC,EF⊥BC,ED⊥AB,∴EF=DE=2,∴△BCE的面积BC×EF=5.故选:A.25.【解答】解:∵∠1=∠2,∵∠1+∠DAC=∠2+∠DAC,∴∠BAC=∠DAE,A、符合SAS定理,即能推出△ABC≌△ADE,故本选项错误;B、符合ASA定理,即能推出△ABC≌△ADE,故本选项错误;C、不符合全等三角形的判定定理,即不能推出△ABC≌△ADE,故本选项正确;D、符合AAS定理,即能推出△ABC≌△ADE,故本选项错误;故选:C.26.【解答】解:A、所有的等边三角形都是全等三角形,错误;B、全等三角形是指面积相等的三角形,错误;C、周长相等的三角形是全等三角形,错误;D、全等三角形是指形状相同大小相等的三角形,正确.故选:D.27.【解答】解:由图形△ABC和△ADC有公共边,结合条件AB=AD,故可再加一组边,和公共边与已知一组边的夹角相等,即当CB=CD或∠BAC=∠DAC时△ABC≌△ADC,当∠B=∠D时,如图,连接BD,∵AB=AD,∴∠ABD=∠ADB,∴∠CBD=∠CDB,∴BC=DC,且AC=AC,∴△ABC≌△ADC(SSS),所以能使△ABC≌△ADC的条件有3个,故选:C.28.【解答】解:①两直角边对应相等,两直角相等,所以根据SAS可以判定两直角边对应相等的两个直角三角形全等.故①正确;②两锐角对应相等的两个直角三角形不一定全等,因为对应边不一定相等.故②错误;③斜边和一直角边对应相等的两个直角三角形,可以根据HL判定它们全等.故③正确;④一锐角和斜边对应相等的两个直角三角形,可以根据AAS判定它们全等.故④正确;⑤一锐角和一边对应相等的两个直角三角形,可以由“直角三角形两个锐角互余”的性质推知另一锐角对应相等,所以根据AAS,或ASA都可判定它们全等.故⑤正确.综上所述,正确的说法有4个.故选:C.29.【解答】解:∵AD=AD、∠ADB=∠ADC、BD=CD∴(1)△ABD≌△ACD正确;∴(2)AB=AC正确;(3)∠B=∠C正确;∠BAD=∠CAD∴(4)AD是△ABC的角平分线.故选:D.30.【解答】解:∵在△OAD和△OBC中,,∴△OAD≌△OBC(SAS)∴∠OBC=∠OAD,∵∠OAD=180°﹣∠O﹣∠D=95°,∴∠OBC=95°,故选:A.31.【解答】解:∵∠A=60°,∠B=50°,∴∠C=180°﹣∠A﹣∠B=70°,∵△ABC≌△DEF,∴∠F=∠C,∵∠C=70°,∴∠F=70°,故选:C.32.【解答】解:作DH⊥AB于H,∵AD平分∠BAC,∠C=90°,DH⊥AB,∴DH=DC=6,即点D到AB的距离是6,故选:D.33.【解答】解:∵PD⊥AB,PE⊥AC,∴∠ADP=∠AEP=90°,在Rt△ADP和△AEP中,∴Rt△ADP≌△AEP(HL),故选:D.34.【解答】解:∵△ABC≌△EFD,∴AC=DE,∵EC=4,CD=3,∴DE=7,∴AC=7,故选:C.35.【解答】解:观察图形可知,图形(1)、图形(2)、图形(3);都符合要求;图形(4)点N在线段AB的延长线上,点M在线段AB的反向延长线上,不符合要求.故画的不正确的是丁同学.故选:D.。



期末复习专题三:全等三角形与轴对称全等三角形1. 全等三角形的概念及性质;2. 三角形全等的判定;3. 角平分线的性质及判定。
知识点一:证明三角形全等的思路通过对问题的分析,将解决的问题归结到证明某两个三角形的全等后,采用哪个全等判定定理加以证明,可以按下图思路进行分析:⎧→⎧⎪⎪→⎨⎪⎪⎪→⎩⎪⎪→→⎧⎪⎪→⎧⎪⎪⎨⎨⎪→⎨⎪⎪⎪⎪⎪→⎩⎩⎪⎪→⎧⎪⎨→⎪⎩⎪⎩SAS SSSHL AAS SAS ASAAAS ASA AAS 找夹角已知两边找第三边找直角边为角的对边找任一角找夹角的另一边已知一边一角边为角的邻边找夹边的另一角找边的对角找夹边已知两角找任一对边 切记:“有三个角对应相等”和“有两边及其中一边的对角对应相等”的两个三角形不一定全等。
例1. 如图,,,,A F E B 四点共线,AC CE ⊥,BD DF ⊥,AE BF =,AC BD =。
求证:ACF BDE ∆≅∆。
知识点二:构造全等三角形例2. 如图,在ABC ∆中,BE 是∠ABC 的平分线, AD BE ⊥,垂足为D 。
求证:21C ∠=∠+∠。
例3. 如图,在ABC ∆中,AB BC =,90ABC ∠=。
F 为AB 延长线上一点,点E 在BC上,BE BF =,连接,AE EF 和CF 。
求证:AE CF =。
知识点三:常见辅助线的作法1. 连接四边形的对角线例4. 如图,AB //CD ,AD //BC ,求证:AB CD =。
2. 作垂线,利用角平分线的知识例5. 如图,,AP CP 分别是ABC ∆外角MAC ∠和NCA ∠的 平分线,它们交于点P 。
求证:BP 为MBN ∠的平分线。
例6. 如图,D 是ABC ∆的边BC 上的点,且CD AB =,ADB BAD ∠=∠,AE 是ABD ∆的中线。
求证:2AC AE =。
解答过程:延长AE 至点F ,使EF AE =,连接DF 在ABE ∆与FDE ∆中 AE FE AEB FED BE DE =⎧⎪∠=∠⎨⎪=⎩∴ABE FDE ∆≅∆(SAS) ∴B EDF ∠=∠ADF ADB EDF ∠=∠+∠,ADC BAD B ∠=∠+∠ 又ADB BAD ∠=∠ ∴ADF ADC ∠=∠AB DF =,AB CD = ∴DF DC =在ADF ∆与ADC ∆中 AD AD ADF ADC DF DC =⎧⎪∠=∠⎨⎪=⎩∴ADF ADC ∆≅∆(SAS) ∴AF AC = 又2AF AE = ∴2AC AE =。

第14章《全等三角形》期末总复习资料(通用5篇)第14章《全等三角形》期末总复习资料篇1本章需要理解掌握的知识点有:一、全等三角形的定义(能够完全重合的两个三角形叫做全等三角形);二、在全等三角形中找对应边和对应角1、公共边是对应边;2、对应角的对边是对应边;3、公共角是对应角;4、对顶角是对应角;5、对应边的对角是对应角。
三、全等三角形的性质:全等三角形的对应边相等、对应角相等。
全等三角形的周长相等、面积相等全等三角形的对应线段都相等四、判定三角形全等的方法:基本事实:sas,asa,sss, 定理aas,判定直角三角形全等的方法:基本事实:sas,asa,sss, 定理aas, hl五、证明题的思考思路:拿到证明题首先看是证明什么的,比如是要证明线段相等,那就要看这两条线段在哪两个三角形中,结合图形看一看这两个三角形是否全等,结合全等证明的依据看全等条件可够,不够的条件能否从其他已知条件中得到;再结合已知条件看从给的已知条件能得到什么,两头一凑,基本上证明思路就出来了。
六、证明角相等的依据1、由角平分线得角相等;2、同角或等角的余角相等3、同角或等角的补角相等3、由平行线得角相等或角的互补;4、三角形内角和是180度;5、全等三角形的对应角相等;6、三角形的外角等于与它不相邻的两内角和;七、证明线段相等的依据全等三角形的对应边相等八、证明角不等的依据三角形的外角大于与它不相邻的任一内角九、证明线段不等的依据三角形两边之和大于第三边图形平移不改变图形形状和大小,只改变位置。
第14章《全等三角形》期末总复习资料篇2教师在吃透教材、简析教材内容、教学目的、教学重点、难点的基础上,遵循整体构思、融为一体、综合论述的原则,分块写清,分步阐述教学内容,以进一步提高教学效果。
下面是由小编为大家带来的关于《全等三角形》,希望能够帮到您!尊敬的各位评委老师:大家好!今天我说课的题目是人教版数学八年级上册第十一章第1节《全等三角形》。
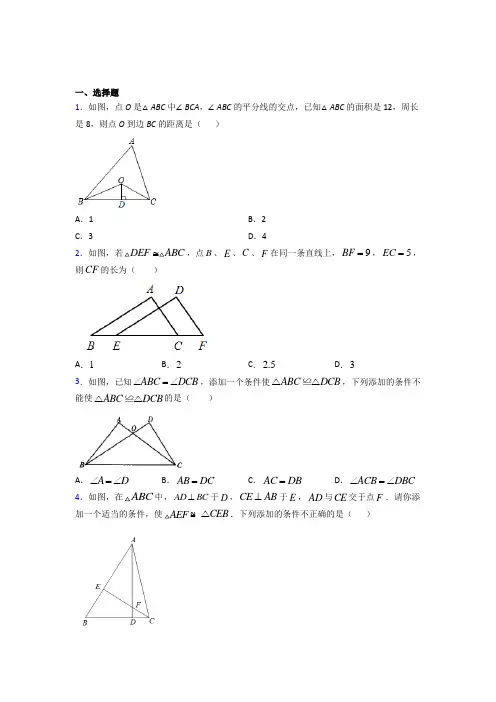
一、选择题1.如图,点O 是△ABC 中∠BCA ,∠ABC 的平分线的交点,已知△ABC 的面积是12,周长是8,则点O 到边BC 的距离是( )A .1B .2C .3D .42.如图,若DEF ABC ≅,点B 、E 、C 、F 在同一条直线上,9BF =,5EC =,则CF 的长为( )A .1B .2C .2.5D .33.如图,已知ABC DCB ∠=∠,添加一个条件使ABC DCB △△≌,下列添加的条件不能使ABC DCB △△≌的是( )A .A D ∠=∠B .AB DC = C .AC DB =D .ACB DBC ∠=∠ 4.如图,在ABC 中,AD BC ⊥于D ,CE AB ⊥于E ,AD 与CE 交于点F .请你添加一个适当的条件,使AEF ≌CEB △.下列添加的条件不正确的是( )A .EF EB = B .EA EC = C .AF CB =D .AFE B ∠=∠ 5.如图,在△ABC 中,AB=5,AC=3,AD 是BC 边上的中线,AD 的取值范围是( )A .1<AD <6B .1<AD <4C .2<AD <8 D .2<AD <4 6.在平面直角坐标系xOy 中,以原点O 为圆心,任意长为半径作弧,分别交x 轴的负半轴和y 轴的正半轴于A 点,B 点,分别以点A ,点B 为圆心,AB 的长为半径作弧,两弧交于P 点,若点P 的坐标为(m ,n),则下列结论正确的是( )A .m =2nB .2m =nC .m =nD .m =-n7.如图,BD 是四边形ABCD 的对角线, AD//BC ,AB AD <,分别过点A ,C 作AE BD ⊥,CF BD ⊥,垂足分别为点E ,F ,若BE DF =,则图中全等的三角形有( )A .1对B .2对C .3对D .4对8.如图,给出下列四组条件:①AB=DE ,BC=EF ,AC=DF ;②AB=DE ,∠B=∠E ,BC=EF ;③∠B=∠E ,BC=EF ,∠C=∠F ;④AB=DE ,AC=DF ,∠B=∠E .其中,能使△ABC ≌△DEF 的条件共有( )A .1组B .2组C .3组D .4组9.下列命题的逆命题是假命题的是( )A .直角三角形两锐角互余B .全等三角形对应角相等C .两直线平行,同位角相等D .角平分线上的点到角两边的距离相等 10.到ABC 的三条边距离相等的点是ABC 的( )A .三条中线的交点B .三条边的垂直平分线的交点C .三条高的交点D .三条角平分线的交点 11.如图,点C ,D 在线段AB 上,AC DB =,AE //BF ,添加以下哪一个条件仍不能判定△AED ≌△BFC ( )A .ED CF =B .AE BF =C .E F ∠=∠D .ED //CF二、填空题12.如图所示的是一张直角ABC 纸片(90C ∠=︒),其中30BAC ∠=︒,如果用两张完全相同的这种纸片恰好能拼成如图2所示的ABD △,若2BC =,则ABD △的周长为______.13.如图,在ABC 中,=6AB ,=4AC ,点D ,E 分别在边AB ,AC 上,2BD AE CE ===,//CE AB 交DE 的延长线于点F ,则CF 的长为_____________.14.如图,△ABC≌△DEF,由图中提供的信息,可得∠D=__________°.15.如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t(s),则当△ACP与△BPQ全等时,点Q的运动速度为__cm/s.∠'=___度.16.如图所示,ABC≅△AB C'',20∠'=︒,BABCAC△的面积是______ 17.如图,ABC中,∠C=90°,AD平分∠BAC,AB=5,CD=2,则ABD18.如图,在四边形ABCD 中,90A ∠=︒,3AD =,连接BD ,BD CD ⊥,ADB C ∠=∠.若P 是BC 边上一动点,则DP 长的最小值为_______.19.已知△ABC ≌△DEF ,△ABC 的三边分别为3,m ,n ,△DEF 的三边分别为5,p ,q .若△ABC 的三边均为整数,则m+n+p+q 的最大值为________.20.如图,//AD BC ,ABC ∠的角平分线BP 与BAD ∠的角平分线AP 相交于点P ,作PE AB ⊥于点E .若9PE =,则两平行线AD 与BC 间的距离为_______.21.如图,已知点(44)A -,,一个以A 为顶点的45︒角绕点A 旋转,角的两边分别交x 轴正半轴,y 轴负半轴于E 、F ,连接EF .当△AEF 直角三角形时,点E 的坐标是________.三、解答题22.(1)如图,∠MAB =30°,AB =2cm ,点C 在射线AM 上,画图说明命题“有两边和其中一边的对角分别相等的两个三角形全等”是假命题,请画出图形,并写出你所选取的BC 的长约为 cm (精确到0.lcm ).(2)∠MAB为锐角,AB=a,点C在射线AM上,点B到射线AM的距离为d,BC=x,若△ABC的形状、大小是唯一确定的,则x的取值范围是.23.在ABC中,AD是ABC的高,30B,52C︒∠=(1)尺规作图:作ABC的角平分线AE(2)求DAE∠的大小.24.如图,点P是锐角∠ABC内一点,BP平分∠ABC,点M在边BA上,点N在边BC上,且PM=PN.求证:∠BMP+∠BNP=180°.25.(1)问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点且∠EAF=60°,探究图中线段BE、EF、FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明ABE≌ADG,再证明AEF≌AGF,可得出结论,他的结论应是______________;(2)探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF12=∠BAD,上述结论是否仍然成立,并说明理由;(3)实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以45海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以60海里/小时的速度前进,2小时后,指挥中心观测到甲、乙两地分别到达E、F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.一、选择题1.如图,在△ABC 中,AB=AC ,AB >BC ,点D 在BC 边上,BD=12DC ,∠BED=∠CFD=∠BAC ,若S △ABC =30,则阴影部分的面积为( )A .5B .10C .15D .202.如图,在ABC 中,8AB AC ==厘米,6BC =厘米,点D 为AB 的中点.如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上,由C 点向A 点运动,为了使BPD CPQ △≌△,点Q 的运动速度应为( )A .1厘米/秒B .2厘米/秒C .3厘米/秒D .4厘米/秒 3.芜湖长江三桥是集客运专线、市域轨道交通、城市主干道路于一体的公铁合建桥梁,2020年9月29日公路段投入运营,其侧面示意图如图所示,其中AB CD ⊥,现添加以下条件,不能判定ABC ABD △≌△的是( )A .ACB ADB ∠=∠B .AB BD =C .AC AD = D .CAB DAB ∠=∠4.如图,,,AB AD CB CD AC BD ==、相交于点O ,则下列说法中正确的个数是( ) ①OD OB =;②点O 到CB CD 、的距离相等;③BDA BDC ∠=∠;④BD AC ⊥A .4B .3C .2D .15.如图,在ABC 和AEF 中,EAC BAF ∠=∠,EA BA =,添加下面的条件:①EAF BAC ∠=∠;②E B ∠=∠;③AF AC =;④EF BC =,其中可以得到ABC AEF ≌△△的有( )个.A .1B .2C .3D .46.下列说法正确的是( )①近似数232.610⨯精确到十分位;②2()2--38-2--38-③如图所示,在数轴上点P 所表示的数为15-;④用反证法证明命题“一个三角形最多有一个钝角”时,首先应假设“这个三角形中有两个钝角”;⑤如图,在ABC 内一点P 到这三条边的距离相等,则点P 是三个角平分线的交点.A .1B .2C .3D .47.点Р在AOB ∠的角平分线上,点Р到OA 边的距离等于5,点Q 是OB 边上的任意一点,则下列选项正确的是( )A .5PQ >B .5PO ≥C . 5PQ <D .5PO ≤ 8.如图,在Rt ABC △中,90C ∠=︒,CAB ∠的平分线交BC 于点D ,且DE 所在直线是AB 的垂直平分线,垂足为E .若3DE =,则BC 的长为( ).A .6B .7C .8D .99.如图,已知△ABC 的周长是20,OB ,OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于,且OD=2,△ABC 的面积是( )A .20B .24C .32D .4010.下列说法正确的是 ( )A .一直角边对应相等的两个直角三角形全等B .斜边相等的两个直角三角形全等C .斜边相等的两个等腰直角三角形全等D .一边长相等的两个等腰直角三角形全等 11.如图,已知,CAB DAE ∠=∠,AC AD =.下列五个选项:①AB AE =,②BC ED =,③C D ∠=∠,④B E ∠=∠,⑤12∠=∠,从中任选一个作为已知条件,其中能使ABC AED ≌△△的条件有( )A .2个B .3个C .4个D .5个二、填空题12.如图,AC=BC ,请你添加一个条件,使AE=BD .你添加的条件是:________.13.如图,在△ABC 中,∠ABC 的平分线与外角∠ACE 的平分线交于点D ,若∠D =20°,则∠A =_____.14.如图,△ABC ≌△A'B'C',其中∠A =35°,∠C =25°,则∠B'=_____.15.如图,四边形ABDC 中,对角线AD 平分BAC ∠,136ACD ∠=︒,44BCD ∠=︒,则ADB ∠的度数为_____16.如图,AD 为∠CAF 的角平分线,BD=CD ,∠DBC=∠DCB ,∠DCA=∠ABD ,过D 作DE ⊥AC 于E ,DF ⊥AB 交BA 的延长线于F ,则下列结论:①△CDE ≌△BDF ;②CE=AB+AE ;③∠DAF=∠CBD .其中正确的结论有_____.(填序号)17.如图所示,己知ABC ∆的周长是22,,OB OC 分别平分ABC ∠和ACB OD BC D ∠⊥,于,且3OD =,则ABC ∆的面积是__________.18.如图,在四边形ABCD 中,90A ∠=︒,3AD =,连接BD ,BD CD ⊥,BD 平分ABC ∠.若P 是BC 边上一动点,则DP 长的最小值为______.19.如图,射线OC 是∠AOB 的角平分线,D 是射线OC 上一点,DP ⊥OA 于点P ,DP =5,若点Q 是射线OB 上一点,OQ =4,则△ODQ 的面积是__________.20.如图,AB =8cm ,AC =5cm ,∠A =∠B ,点P 在线段AB 上以2cm/s 的速度由点A 向B 运动,同时,点Q 以x cm/s 的速度从点B 出发在射线BD 上运动,则△ACP 与△BPQ 全等时,x 的值为_____________21.如图,12∠=∠,要用“SAS ”判定ADC BDC ≌△△,则可加上条件__________.三、解答题22.如图,点A 、D 、B 、E 在一条直线上,BC 与DF 交于点G ,AD BE =,//BC EF ,BC EF =.求证:ABC DEF △≌△.23.如图,点E 在线段BD 上,已知,,AB AC AD AE BE CD ===.(1)求证:BAC EAD ∠=∠.(2)写出123∠∠∠、、之间的数量关系,并予以证明.24.如图,AB CB ⊥,DC CB ⊥,点E 、F 在BC 上,BE CF =,再添加一个什么条件后可推出AF DE =,写出添加的条件并完成证明.25.小敏在学习了几何知识后,对角的知识产生了兴趣,进行了如下探究:(1)如图1,∠AOB =90°,在图中动手画图(不用写画法).在∠AOB 内部任意画一条射线OC ;画∠AOC 的平分线OM ,画∠BOC 的平分线ON ;用量角器量得∠MON =______. (2)如图2,∠AOB =90°,将OC 向下旋转,使∠BOC =30°,仍然分别作∠AOC ,∠BOC 的平分线OM ,ON ,能否求出∠MON 的度数,若能,求出其值,若不能,试说明理由.一、选择题1.如图,AB ∥CD ,BE 和CE 分别平分∠ABC 和∠BCD ,AD 过点E ,且AD ⊥AB ,点P 为线段BC 上一动点,连接PE .若AD =14,则PE 的最小值为( )A .7B .10C .6D .52.芜湖长江三桥是集客运专线、市域轨道交通、城市主干道路于一体的公铁合建桥梁,2020年9月29日公路段投入运营,其侧面示意图如图所示,其中AB CD ⊥,现添加以下条件,不能判定ABC ABD △≌△的是( )A .ACB ADB ∠=∠B .AB BD =C .AC AD = D .CAB DAB ∠=∠3.如图,在ABC 中,AB AC =,点D ,E 在BC 上,连接AD ,AE ,若只添加一个条件使DAB EAC ∠=∠,则添加的条件不能为( )A .BD CE =B .AD AE =C .BE CD = D .DA DE = 4.如图,已知ABC DCB ∠=∠,添加一个条件使ABC DCB △△≌,下列添加的条件不能使ABC DCB △△≌的是( )A .A D ∠=∠B .AB DC = C .AC DB =D .ACB DBC ∠=∠ 5.工人师傅常用直角尺平分一个角,做法如下:如图所示,在∠AOB 的边OA ,OB 上分别取OM =ON ,移动直角尺,使直角尺两边相同的刻度分别与M ,N 重合(即CM =CN ).此时过直角尺顶点C 的射线OC 即是∠AOB 的平分线.这种做法的道理是( )A .HLB .SASC .SSSD .ASA6.如图,点O 在ABC 内,且到三边的距离相等.若110BOC ∠=°,则A ∠的度数为( )A .40︒B .45︒C .50︒D .55︒7.如图,在Rt ABC △中,90C ∠=︒,CAB ∠的平分线交BC 于点D ,且DE 所在直线是AB 的垂直平分线,垂足为E .若3DE =,则BC 的长为( ).A .6B .7C .8D .98.如图,已知∠A=∠D , AM=DN ,根据下列条件不能够判定△ABN ≅△DCN 的是( )A .BM ∥CNB .∠M=∠NC .BM=CND .AB=CD 9.如图,OB 平分∠MON ,A 为OB 的中点,AE ⊥ON ,EA=3,D 为OM 上的一个动点,C 是DA 延长线与BC 的交点,BC //OM ,则CD 的最小值是( )A .6B .8C .10D .1210.如图,在下列条件中,不能判断△ABD ≌△BAC 的条件是( )A .∠D=∠C , ∠BAD=∠ABCB .BD=AC , ∠BAD=∠ABC C .∠BAD=∠ABC , ∠BAD=∠ABCD .AD=BC ,BD=AC11.如图,在Rt ABC 和Rt ADE △中,90,,ACB AED AB AD AC AE ∠=∠===,则下列说法不正确的是( )A .BC DE =B .BAE DAC ∠=∠ C .OC OE =D .EAC ABC ∠=∠二、填空题12.如图,AC=BC ,请你添加一个条件,使AE=BD .你添加的条件是:________.13.如图,△ABC 中,∠ACB =90°,点D 在边AC 上,DE ⊥AB 于点E ,DC =DE ,∠A =32°,则∠BDC 的度数为________.14.如图,已知四边形,90,3,4,5,ABCD B AB BC AC ︒∠====180BAD CAD ︒∠+∠=,180BCD ACD ︒∠+∠=,则四边形ABCD 的面积是_________.15.如图,D ,E 分别是AB ,AC 上的点,AD=AE ,请添加一个条件,使得ABE ≌ACD .这个条件可以为_____(只填一个条件即可).16.如图,在△ABC 中,∠ACB =120°,BC =4,D 为AB 的中点,DC ⊥BC ,则点A 到直线CD 的距离是_____.17.如图,ABC 的三边AB 、BC 、CA 长分别是10、15、20,三条角平分线交于O 点,则::ABO BCO CAO S S S 等于__________.18.如图,在Rt ABC △中,90C ∠=︒,以顶点A 为圆心,任意长为半径画弧,分别交AC ,AB 于点M ,N ,再分别以点M ,N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,作射线AP 交BC 于点D .若3CD =,10AB =,则ABD △的面积是______.19.如图,已知ABC 的周长是8,OB ,OC 分别平分ABC ∠和ACB ∠,OD BC 于D ,且3OD =,ABC 的面积是______.20.如图,△ACB 和△DCE 中,AC =BC ,∠ACB =∠DCE =90°,∠ADC =∠BEC ,若AB =17,BD =5,则S △BDE =_______.21.如图,12∠=∠,要用“SAS ”判定ADC BDC ≌△△,则可加上条件__________.三、解答题22.如图,点C 在BE 上,AB ⊥BE ,DE ⊥BE ,且AB =CE ,AC =CD .判断AC 和CD 的关系并说明理由.23.如图所示,A ,C ,E 三点在同一直线上,且ABC DAE △△≌.(1)求证:BC DE CE =+;(2)当ABC 满足什么条件时,//BC DE ?24.如图,A 、D 、F 、B 在同一直线上,EF ∥CD ,AE ∥BC ,且AD =BF .求证:AE =BC25.如图,在四边形ABCD 中,//AD BC ,E 为AC 的中点,连接DE 并延长,交BC 于点F .(1)求证:DE EF =.(2)若12AD =,:2:3BF CF =,求BC 的长.。
湖南省数学八年级上学期期末复习专题3 全等三角形的性质、判定与应用姓名:________ 班级:________ 成绩:________一、单选题 (共10题;共30分)1. (3分)用两个全等的三角形一定不能拼出的图形是()A . 等腰三角形B . 直角梯形C . 菱形D .矩形2. (3分) (2020七下·张掖月考) 下列说法中正确的是()A . 面积相等的两个图形是全等形B . 周长相等的两个图形是全等形C . 所有正方形都是全等形D . 能够完全重合的两个图形是全等形3. (3分) (2018八上·达孜期中) 下列图形中有稳定性的是()A . 长方形B . 多边形C . 锐角三角形D . 平行四边形4. (3分) (2017八上·南宁期中) 如图所示,△ABC≌△CDA,且AB=CD,则下列结论错误的是()A . ∠1=∠2B . AC=CAC . ∠B=∠DD . AC=BC5. (3分)如图所示,某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是()A . 带①去B . 带②去C . 带③去D . ①②③都带去6. (3分) (2019八上·渝中期中) 下面是作角等于已知角的尺规作图过程,要说明∠A′O′B′=∠AOB,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是()A . 边边边B . 边角边C . 角边角D . 角角边7. (3分) (2020八上·裕安期末) 如图,点A,D,C,F在一条直线上,AB=DE,∠A=∠EDF,下列条件不能判定△ABC≌△DEF的是()A . AD=CFB . ∠BCA=∠FC . ∠B=∠ED . BC=EF8. (3分)如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD 的面积为y,则y与x之间的函数关系式是()A .B .C .D .9. (3分)已知点在线段的中垂线上,点在线段的中垂线外,则().A .B .C .D . 不能确定10. (3分)在正方形网格中,∠AOB的位置如图所示,到∠AOB两边距离相等的点应是()A . M点B . N点C . P点D . Q点二、填空题 (共6题;共24分)11. (4分) (2020八上·上虞月考) 下列命题中逆命题是真命题的是________.(写序号)( 1 )直角三角形两条直角边的平方和等于斜边的平方;( 2 )等腰三角形两腰上的高线相等;( 3 )若三条线段是三角形的三边,则这三条线段满足;( 4 )角的内部,到角两边距离相等的点在这个角的平分线上.( 5 )全等三角形的面积相等.12. (4分)(2020·温岭模拟) 如图,已知点E为矩形ABCD内的点,若EB=EC,则EA________ED(填“>”、“<”或“=”)13. (4分) (2019八上·宣城期末) 如图,,与交于点O,在不添加任何辅助线的前提下要使,则需添加条件________.14. (4分)如图,在四边形ABCD中,AB∥CD,连接BD.请添加一个适当的条件,使△ABD≌△CDB.(只需写一个)________15. (4分)(2012·贺州) 如图,在菱形ABCD中,边AB的垂直平分线与对角线AC相交于点E,∠ABC=140°,那么∠EDC=________.16. (4分) (2020八上·达拉特旗期中) 如图,在ΔAB C中,AD是∠BAC的平分线,AB=3cm,AC=2cm,则S△ABD:S△ACD=________.三、解答题 (共8题;共66分)17. (10分) (2020八上·中山期末) 如图,已知△ABC中,∠BAC=23°,∠BCA=125°。
湖南省邵阳市数学八年级上学期期末专题复习专题3:全等三角形
姓名:________ 班级:________ 成绩:________
一、单选题 (共4题;共8分)
1. (2分) (2018八上·梁园期末) 图中的两个三角形全等,则等于().
A .
B .
C .
D .
2. (2分) (2020八上·丹江口期末) 已知: .求作:一个角,使它等于 .步骤如下:如图,
( 1 )作射线
( 2 )以为圆心,任意长为半径作弧,交于,交于;
( 3 )以为圆心,为半径作弧,交于 ;
( 4 )以为圆心,为半径作弧,交弧于;
( 5 )过点作射线 .则就是所求作的角.请回答:该作图的依据是()
A .
B .
C .
D .
3. (2分) (2016八上·腾冲期中) 下列命题中,正确的是()
A . 形状相同的两个三角形是全等形
B . 面积相等的两个三角形全等
C . 周长相等的两个三角形全等
D . 周长相等的两个等边三角形全等
4. (2分)(2019·云南模拟) 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=4,则AE的长为()
A .
B . 2
C . 3
D . 4
二、填空题 (共3题;共3分)
5. (1分) (2019八上·正安月考) 已知等腰三角形ABC的周长为25,AB=10,则BC为________.
6. (1分) (2019七下·富宁期中) 小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块)你认为将其中的哪一块带去,就能配一块与原来一样大小的三角形?应该带________.依据________
7. (1分)(2018·东营) 如图,在Rt△ABC中,∠B=90°,以顶点C为圆心,适当长为半径画弧,分别交AC,BC于点E,F,再分别以点E,F为圆心,大于 EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=3,AC=10,则△ACD的面积是________.
三、解答题 (共2题;共10分)
8. (5分) (2016八上·怀柔期末) 如图,点C,D在线段BF上,AB∥DE,AB=DF,∠A=∠F,求证:BC=DE.
9. (5分) (2015八上·武汉期中) 已知:如图,在△ABC中,点D是BC的中点,过点D作直线交AB,CA
的延长线于点E,F.当BE=CF时,求证:AE=AF.
四、作图题 (共1题;共6分)
10. (6分) (2020八上·石景山期末) 已知:如图△ABC,直线l.求作:点P.使得点P在直线l上,且点P、点A、点B构成的三角形为等腰三角形(保留作图痕迹,不必写出作法).
解:
(1)满足条件的点共有________个;
(2)在图中用尺规作图作出满足条件的点P(保留作图痕迹,不必写出作法).
五、综合题 (共4题;共36分)
11. (10分)(2016·崂山模拟) 已知,如图,▱ABCD中,BC=8cm,CD=4cm,∠B=60°,点M从点D出发,沿DA方向匀速运动,速度为2cm/s,点N从点B出发,沿BC方向匀速运动,速度为1cm/s,过M作MF⊥CD,垂足为F,延长FM交BA的延长线于点E,连接EN,交AD于点O,设运动时间为t(s)(0<t<4),解答下列问题:
(1)当t为何值时,△AEM≌△DFM?
(2)连接AN,MN,设四边形ANME的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形ANME的面积是▱ABCD面积的?若存在,求出相应的t值,若不存
在,说明理由;
(4)连接AC,交EN于点P,当EN⊥AD时,求线段OP的长度.
12. (1分) (2020八上·兰山期中) 如图,在中,,平分,,
,则点D到的距离是________.
13. (15分) (2020八上·覃塘期末) 已知:,点A、B分别在射线OM、ON上(A、B均不与重合),以AB为边在∠MON的内部作等边三角形ABC,连接OC.
(1)如图1,当OA=OB时,求证:平分 .
(2)如图2,当OA≠OB时,过点C作CD⊥OM,CE⊥ON,垂足分别为D、E.求证:OD=OE.(注:四边形的内角和为 )
14. (10分)如图,已知直线l1:y=x+2与直线l2:y=﹣kx+4(k≠0)相交于点F,直线l1 , l2分别交x轴于点E,G.长方形ABCD的顶点C,D分别在l2和y轴上,顶点A,B都在x轴上,且点B与点E重合,点A与点O重合,长方形ABCD的面积是12.
(1)求k的值;
(2)求证:△EFG是等腰直角三角形;
(3)若长方形ABCD从原地出发,沿x轴正方向以每秒1个单位长度的速度平移,设移动时间为t秒,长方形ABCD与△EFG重叠部分的面积为S.
①当0≤t≤1时,求S的最大值;
②当1<t≤4时,直接写出S与t之间的函数关系式(要求写出自变量t的取值范围).
参考答案一、单选题 (共4题;共8分)
答案:1-1、
考点:
解析:
答案:2-1、
考点:
解析:
答案:3-1、
考点:
解析:
答案:4-1、考点:
解析:
二、填空题 (共3题;共3分)答案:5-1、
考点:
解析:
答案:6-1、
考点:
解析:
答案:7-1、
考点:
解析:
三、解答题 (共2题;共10分)
答案:8-1、
考点:
解析:
答案:9-1、
考点:
解析:
四、作图题 (共1题;共6分)
答案:10-1、
答案:10-2、
考点:
解析:
五、综合题 (共4题;共36分)答案:11-1、
答案:11-2、答案:11-3、
答案:11-4、考点:
解析:
答案:12-1、考点:
解析:
答案:13-1、
答案:13-2、考点:
解析:
答案:14-1、
答案:14-2、
考点:解析:。