微电子电路分析方法与定理

电子电路中的电路分析方法有哪些电路分析是电子电路中非常重要的一项技术，可以帮助工程师们理解电路的工作原理并解决电路中的问题。

本文将介绍一些常用的电路分析方法。

1. 网络定理网络定理是分析电子电路中的电压和电流分布的一种方法。

其中，基尔霍夫定律是最常用的网络定理之一。

它分为基尔霍夫电压定律（KVL）和基尔霍夫电流定律（KCL）。

KVL指出在闭合回路中电压的代数和为零，而KCL则表明在电路中的节点处电流的代数和为零。

通过使用这两个定律，工程师们可以建立方程组，进而求解电路中的未知电压和电流。

2. 等效电路模型等效电路模型是将复杂的电路简化为较为简单的等效电路，以便更好地进行分析。

最常用的等效电路模型包括电阻、电容和电感等元件。

通过将电路中的各个元件替换为其相应的等效电路模型，可以简化电路结构，并且能够更容易地进行分析和计算。

3. 超节点分析当电路中存在多个节点之间相同电压的情况时，可以使用超节点分析法。

超节点分析法将这些节点看作一个整体，从而简化分析过程。

通过识别并将这些节点连接起来，可以构建超节点方程，可以更简单地计算电路中的电压和电流。

4. 瞬态响应分析瞬态响应分析用于分析电路的初始和瞬时响应。

当电路中存在电源切换、电路开关或其他突变的情况时，瞬态响应分析可以帮助工程师们了解电路在这些变化下的响应情况。

通过对电路进行微分方程建模，可以求解电路中元件的电压和电流随时间的变化规律。

5. 频率响应分析频率响应分析主要用于分析电路对输入信号的频率变化的响应情况。

通过对电路进行频域分析，可以得到电路的频率响应曲线，从而了解电路对不同频率信号的传输、滤波和放大能力。

常用的频率响应分析方法包括幅频响应和相频响应。

6. 交流分析法交流分析法适用于分析交流电路，特别是在稳态条件下工作的交流电路。

通过将交流信号看作复数形式，并使用复数分析方法，可以更方便地求解交流电路中的电压、电流和功率等参数。

综上所述，电子电路中的电路分析方法有网络定理、等效电路模型、超节点分析、瞬态响应分析、频率响应分析和交流分析法等。

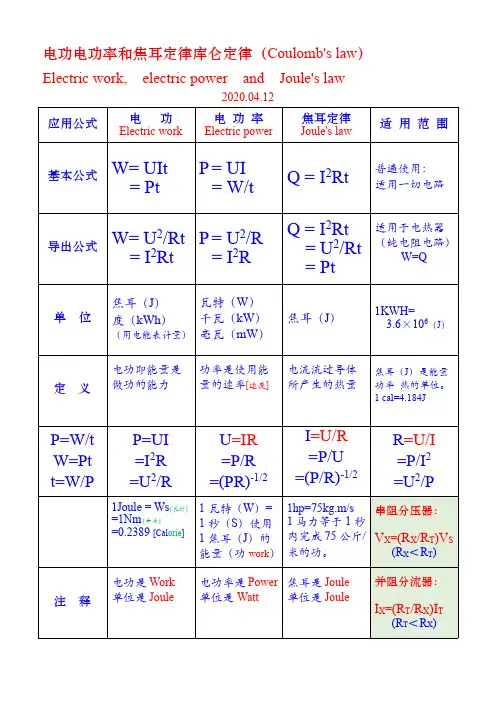
电功电功率和焦耳定律库仑定律（Coulomb's law）Electric work,electric power and Joule's law单位换算⑴1卡(Cal orie)=4.1858518焦耳(J)1焦耳(J)=0.23890000119卡(cal)⑵焦耳--卡路里：1千卡(KCAL)=4.184千焦耳(KJ)1千焦耳(KJ)=0.239千卡(KCAL)1卡=4.184焦耳1焦耳=0.2389卡⑶焦耳--瓦特：1焦耳(J)=1瓦特×秒(W·s)1度(1kw·h)=3.6×10^6焦耳(J)⑷焦耳--牛顿米：1焦耳(J)=1牛顿×米(N·m)名词解释：电功（W）：电流所做的功称为电功（The work done by current is called electric work）单位是焦耳（J）。

电量（Q）：单位是库伦（C）。

1库伦=6.25x1018个电子所带的电量。

1个电子所带的电量为1.6x10-19C。

电量quantity of electricity。

电流（I）：单位是安培（A）。

1安培（1A）=1秒（1S）通过给定截面的总电量是1库伦（1C）。

Q=W/t（W单位焦耳J，t单位秒s）电压（U）：单位是伏特（V）。

移动单位电荷所需要的能量叫电压。

V=W/Q（W单位焦耳J，Q单位库伦C）。

电阻（R）：单位是欧姆（Ω）。

某材料两端若加有1伏特（1V）的电压，如果材料中流过的电流是1安培（1A），则该材料的电阻值为1欧姆（1Ω）R=U/R。

电导G=1/R（S）。

重要定理（10个）⑴（电路）基尔霍夫定律（Kirchhoff laws）基尔霍夫第一定律（KCL）又称基尔霍夫电流定律所有进入某节点的电流的总和等于所有离开这节点的电流的总和。

假设进入某节点的电流为正值，离开这节点的电流为负值，则所有涉及这节点的电流的代数和等于零。

第1篇一、实验背景电路分析是电子技术领域的基础课程，通过对电路的基本原理和特性的研究，培养学生的电路分析和设计能力。

本次实验旨在通过实际操作，加深对电路分析理论的理解，提高电路实验技能。

二、实验目的1. 掌握电路分析方法，包括电路等效变换、电路分析方法、电路特性分析等；2. 学会使用常用电子仪器，如万用表、示波器等；3. 提高电路实验技能，培养严谨的科学态度和团队合作精神。

三、实验内容本次实验主要包括以下内容：1. 电路基本元件的测试与识别；2. 电路等效变换与简化；3. 电路分析方法的应用；4. 电路特性分析；5. 电路实验技能训练。

四、实验步骤1. 实验前准备：熟悉实验原理、步骤，准备好实验器材；2. 测试电路基本元件：使用万用表测试电阻、电容、电感等元件的参数；3. 电路等效变换与简化：根据电路图，运用等效变换和简化方法，将复杂电路转换为简单电路；4. 电路分析方法的应用：根据电路分析方法，分析电路的输入输出关系、电路特性等；5. 电路特性分析：通过实验，观察电路在不同条件下的工作状态，分析电路特性；6. 实验数据记录与分析：记录实验数据，分析实验结果，总结实验经验。

五、实验结果与分析1. 电路基本元件测试：通过测试，掌握了电阻、电容、电感等元件的参数，为后续电路分析奠定了基础；2. 电路等效变换与简化：成功地将复杂电路转换为简单电路，提高了电路分析的效率；3. 电路分析方法的应用：运用电路分析方法，分析了电路的输入输出关系、电路特性等，加深了对电路理论的理解；4. 电路特性分析：通过实验，观察了电路在不同条件下的工作状态，分析了电路特性，为电路设计提供了参考；5. 电路实验技能训练：通过实际操作，提高了电路实验技能，为今后的学习和工作打下了基础。

六、实验总结1. 本次实验加深了对电路分析理论的理解，提高了电路实验技能；2. 通过实验，学会了使用常用电子仪器，为今后的学习和工作打下了基础；3. 培养了严谨的科学态度和团队合作精神，提高了自身综合素质；4. 发现了自身在电路分析方面的不足，为今后的学习指明了方向。

电路实验报告戴维南定理（文章一）：验证戴维南定理实验报告（一）、实验目的1. 验证戴维南定理和诺顿定理的正确性，加深对该定理的理解。

2. 掌握测量有源二端网络等效参数的一般方法。

（二）、原理说明1. 任何一个线性含源网络，如果仅研究其中一条支路的电压和电流，则可将电路的其余部分看作是一个有源二端网络（或称为含源一端口网络）。

戴维南定理指出：任何一个线性有源网络，总可以用一个电压源与一个电阻的串联来等效代替，此电压源的电动势Us等于这个有源二端网络的开路电压Uoc，其等效内阻R0等于该网络中所有独立源均置零（理想电压源视为短接，理想电流源视为开路）时的等效电阻。

诺顿定理指出：任何一个线性有源网络，总可以用一个电流源与一个电阻的并联组合来等效代替，此电流源的电流Is等于这个有源二端网络的短路电流ISC，其等效内阻R0定义同戴维南定理。

Uoc（Us）和R0或者ISC（IS）和R0称为有源二端网络的等效参数。

2. 有源二端网络等效参数的测量方法(1) 开路电压、短路电流法测R0 在有源二端网络输出端开路时，用电压表直接测其输出端的开路电压Uoc，然后再将其输出端短路，用电流表测其短路电流Isc，则等效内阻为如果二端网络的内阻很小，若将其输出端口短路则易损坏其内部元件，因此不宜用此法。

(2) 伏安法测R0 用电压表、电流表测出有源二端网络的外特性曲线，如图3-1所示。

根据外特性曲线求出斜率tgφ，则内阻图3-1也可以先测量开路电压Uoc，再测量电流为额定值IN时的输出端电压值UN，则内阻为(3) 半电压法测R0 如图3-2所示，当负载电压为被测网络开路电压的一半时，负载电阻（由电阻箱的读数确定）即为被测有源二端网络的等效内阻值。

图3-2(4) 零示法测UOC 在测量具有高内阻有源二端网络的开路电压时，用电压表直接测量会造成较大的误差。

为了消除电压表内阻的影响，往往采用零示测量法，如图3-3所示。

零示法测量原理是用一低阻的稳压电源与被测有源二端网络进行比较，当稳压电源的输出电压与有源二端网络的开路电压相等时，电压表的读数将为“0”。

第一篇 电路分析基础【本篇介绍】该篇介绍电路分析的基本概念、基本理论、基本方法和基本定律。

该部分是电路分析的基础。

通过该部分的学习，使同学们掌握分析电路的基本知识与方法，为今后学习和工作打下基础。

第一章 电路的基本概念及基本定律1.1 教学目标本章教学主要目标是让学生掌握电路分析的一些基础知识—基本概念和基本定律。

在基本概念中要明确如何将实际电路转化为电路模型？电路分析中的基本变量有哪些？掌握电路分析的基本定律—基尔霍夫定律和欧姆定律，为学习后面各章打下基础。

1.2 教学内容（1） 电路模型（2） 电路基本变量（3） 基尔霍夫电压定律（KVL ）、基尔霍夫电流定律（KCL ）和欧姆定律 （4） 电路元件1.3 重点、难点指导1.3.1 电路模型。

电路模型就是把实际电路器件构成的电路进行抽象得出来的模型，俗称电路图。

对实际电路进行模型化处理的前提是：假设电路中的基本电磁现象可以分别研究，并且相应的电磁过程都集中在各理想元件内部进行。

即所谓的电路理论的集中化假设。

集中参数元件的主要特点是：元件外形尺寸与其正常工作频率所对应的波长而言小很多。

1.3.2 电路基本变量电路分析中的基本变量为电流、电压和功率，其中tt q t i d )(d )(=)(d )(d )(t q t w t u =)()(d )(d )(t i t u tt w t p ==在应用这些变量分析电路问题时，一定要注意以下三个问题：1. 在电路图中所用到的电流或电压，一定要先设定参考方向，这是求解电路的前提，否则所得结果的正、负值没有意义。

2. 一定要搞清楚某支路上电流和电压方向是关联还是非关联参考方向。

否则无法列出方程。

如图1-1所示，对于网络N 2而言，u 和i 方向是关联的；对于网络N 1而言，u 和i 方向是非关联的。

3. 在计算元件（或网络）的功率时，若u 和i则功率ui p =若u 和i 方向非关联，则功率应写为图1-1 参考方向示例ui p −=若p >0，则说明该元件（或网络）吸收功率；若p <0，则说明该元件（或网络）产生功率。

电路分析知识点总结高中一、电路基本知识1、电流、电压和电阻电流是电荷在电路中的流动，通常用符号I来表示，单位是安培(A)；电压是电路中的电势差，通常用符号V来表示，单位是伏特(V)；电阻是电路中阻碍电流通过的元件，通常用符号R来表示，单位是欧姆(Ω)。

2、基尔霍夫定律基尔霍夫定律包括基尔霍夫电流定律和基尔霍夫电压定律。

基尔霍夫电流定律指出在电路中任意一个节点处，进入该节点的电流之和等于离开该节点的电流之和；基尔霍夫电压定律指出在电路中任意一个闭合回路中，电压源的代数和等于电阻元件两端电压的代数和。

3、电路连接方式电路主要有串联、并联和混合连接方式。

串联是将电路中的元件依次连接在一起，电流流过这些元件时，将会依次经过每一个元件；并联是将多个元件的一端连接在一起，另一端连接在一起，这样电流就会同时流过这些元件；混合连接是将串联和并联方式进行结合，电路中既有串联又有并联。

4、电路中的电压源和电流源电压源是提供固定电压的元件，通常用符号E表示；电流源是提供固定电流的元件，通常用符号I表示。

电压源和电流源在电路中具有重要的作用，通过它们可以提供恒定的电压和电流。

二、电路分析方法1、节点分析节点分析是一种基于基尔霍夫电流定律的电路分析方法。

节点分析的基本思想是先选择一个节点作为参考节点，然后根据基尔霍夫电流定律列出各节点处电流的代数和等式，最后利用这些等式求解电路中各个节点的电流。

2、微分方程法微分方程法是一种用微分方程求解电路中电压和电流的方法。

它的基本思想是根据电路中元件的特性和基尔霍夫定律列出相应的微分方程，然后求解这些微分方程得到电路中电压和电流的变化规律。

3、戴维宁定理戴维宁定理是一种用于简化复杂电路的电路分析方法。

它的基本原理是将电路中的多个元件通过等效电压源和等效电阻替代，从而简化电路分析的过程。

4、电路的稳定性分析电路的稳定性分析是一种用于分析电路稳定性的方法。

它的基本思想是通过改变电路中元件的参数，来分析电路的响应和稳定性。

电路分析戴维南定理与电流计算电路分析是电子工程中非常重要的一部分，它涉及到电路中各个元件的性质和相互关系。

在进行电路分析的过程中，戴维南定理和电流计算是两个基本而关键的概念。

本文将对这两个概念进行详细的介绍和解析。

一、戴维南定理戴维南定理是电路分析中一个非常有用的工具，它可以帮助我们简化复杂的电路，并找到我们所关心的电流或电压数值。

戴维南定理的核心思想是将被测电阻或电源通过一个等效电阻或等效电源替代，从而简化电路的分析过程。

为了更好地理解戴维南定理，我们先来看一个具体的例子。

假设我们有一个包含多个电阻的电路，我们想要计算某一点的电流。

按照戴维南定理，我们可以先将该点与电路中其他分支断开，并用一个电压源来保持该点电势恒定。

接下来，我们需要计算在这个条件下，通过该点的电流。

这个电流即为我们所求的结果。

除了计算电流，戴维南定理也可以用于计算电压。

当我们想要计算电路中某一分支的电压时，可以使用戴维南定理化简电路，并计算在等效电路中的电压值。

二、电流计算电流是电子电路中最基本的物理量之一，它描述了电荷在电路中的流动情况。

在电路分析中，我们常常需要计算电流来确定电路的工作状态和性能。

通常情况下，计算电路中的电流有两种方法：理论计算和实验测量。

理论计算是通过应用基本电路定律和电路分析技巧，结合元件的参数和拓扑结构，来推导出电流的数学表达式。

实验测量则是通过使用电流计或多用表等测量设备，直接测量电路中各个分支的电流值。

在实际应用中，为了确保电流计算的准确性，我们需要注意以下几点：1. 元件参数的准确性：电流计算所依赖的电阻、电容、电感等元件参数应尽可能精确，以避免计算结果的误差。

2. 电路拓扑结构的分析：在进行电流计算之前，需要先了解电路的布置和拓扑结构，分析电路中的节点、支路和回路，以确保计算的有效性。

3. 使用正确的电路定律：在进行电流计算时，需要正确地应用欧姆定律、基尔霍夫定律等电路定律，以确保计算过程的准确性和一致性。

用电路分析方法解决电流和电压问题电路分析方法是解决电流和电压问题的重要工具。

无论是在电子工程领域还是日常生活中，我们都会遇到各种电路问题，如电流的大小、电压的稳定性等。

通过电路分析方法，我们可以准确地计算电路中的电流和电压，从而解决这些问题。

首先，我们需要了解电路中的基本元件。

电路由电源、电阻、电容和电感等元件组成。

电源提供电流，电阻控制电流的大小，电容和电感则影响电压的稳定性。

在电路分析中，我们需要根据电路中的元件参数，来计算电流和电压的数值。

其次，电路分析方法可以通过基本的电路定律来解决问题。

其中，欧姆定律是最基本的定律之一。

它表明电流和电压之间存在线性关系，即电流等于电压除以电阻。

通过欧姆定律，我们可以计算电路中的电流大小。

除了欧姆定律，基尔霍夫定律也是电路分析中常用的方法之一。

基尔霍夫定律分为两个定律：基尔霍夫第一定律和基尔霍夫第二定律。

基尔霍夫第一定律是能量守恒定律，它表明电路中的电流进入节点的总和等于离开节点的总和。

基尔霍夫第二定律是电压环路定律，它表明电路中的电压沿闭合回路的总和等于零。

通过基尔霍夫定律，我们可以建立方程组，从而解决电路中的电流和电压问题。

此外，电路分析方法还包括戴维南定理和诺顿定理。

戴维南定理是将电路中的元件转换为等效电源和等效电阻，从而简化电路分析。

诺顿定理则是将电路中的元件转换为等效电流和等效电阻。

通过戴维南定理和诺顿定理，我们可以将复杂的电路简化为简单的等效电路，从而更方便地计算电流和电压。

除了以上的基本方法，电路分析中还涉及到复杂的数学工具，如复数和拉普拉斯变换。

复数可以用来表示交流电路中的相位差和幅度，从而更准确地计算电流和电压。

拉普拉斯变换则可以将电路中的微分方程转换为代数方程，从而更简便地解决电路问题。

综上所述，电路分析方法是解决电流和电压问题的重要工具。

通过了解电路中的基本元件和运用电路定律，我们可以准确地计算电流和电压的数值。

此外，借助戴维南定理、诺顿定理以及复数和拉普拉斯变换等数学工具，我们可以更方便地解决复杂的电路问题。

电路分析电容与感应公式整理在电路分析中，电容和感应是非常重要的元件，它们在电路中起着关键的作用。

通过合理运用电容和感应的公式，我们可以更好地理解电路的行为和性质，进而设计和优化电路。

本文将对电容和感应的公式进行整理和总结，以便于电路分析的实践应用。

一、电容电容是一种储存电荷的元件，它由两个平行的导体板和介质组成。

电容的性质可以通过带电量（Q）和电压（V）之间的关系来描述。

根据电容的定义，电容的公式为：C = Q / V其中，C表示电容的大小，单位为法拉（F），Q表示电荷的大小，单位为库仑（C），V表示电容两端的电压，单位为伏特（V）。

根据电容的公式，我们可以推导出其他和电容相关的公式，例如：1. 带电量和电压的关系Q = C × V2. 电容的能量E = 1/2 CV^23. 电容的串并联关系对于串联电容，它们的电容值相加，即：1/C = 1/C1 + 1/C2 + ...对于并联电容，它们的电容值直接相加，即：C = C1 + C2 + ...二、感应感应是指当电流通过一根线圈时，线圈内会产生磁场，并且该磁场变化时会产生电流。

感应的公式可以由法拉第电磁感应定律得到，根据法拉第电磁感应定律，感应电动势（ε）与磁通量（Φ）的变化率成正比，即：ε = -dΦ/dt其中，ε表示感应电动势的大小，单位为伏特（V），Φ表示磁通量的大小，单位为韦伯（Wb），t表示时间，单位为秒（s）。

根据感应电动势的公式，我们可以推导出其他和感应相关的公式，例如：1. 磁通量和磁场的关系Φ = B × A其中，Φ表示磁通量的大小，单位为韦伯（Wb），B表示磁场的大小，单位为特斯拉（T），A表示面积，单位为平方米（m^2）。

2. 感应电动势和导线形状的关系ε = -dΦ/dt = -B × dA/dt根据导线的形状和磁场的变化状况，可以通过对面积的微分来求得感应电动势。

3. 磁通量和匝数的关系Φ = B × A = B × N × S其中，N表示线圈匝数，S表示线圈的截面积。