二部图应用

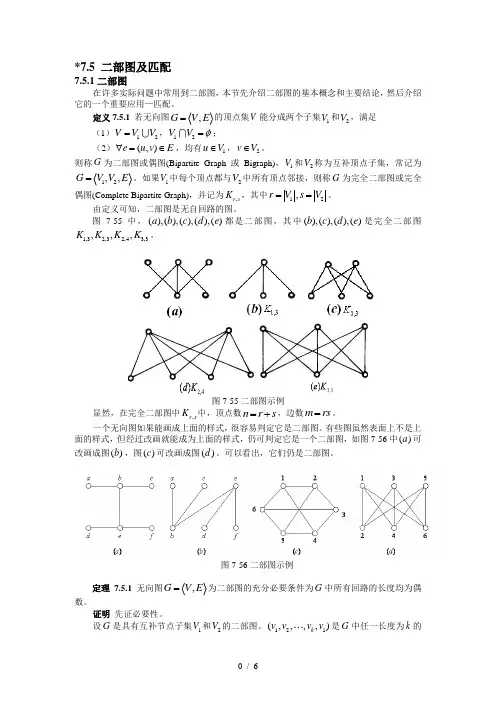
*7.5 二部图及匹配7.5.1二部图在许多实际问题中常用到二部图，本节先介绍二部图的基本概念和主要结论，然后介绍它的一个重要应用—匹配。

定义7.5.1 若无向图,G V E =的顶点集V 能分成两个子集1V 和2V ，满足（1）12V V V =，12V V φ=；（2）(,)e u v E ∀=∈，均有1u V ∈，2v V ∈。

则称G 为二部图或偶图(Bipartite Graph 或Bigraph)，1V 和2V 称为互补顶点子集，常记为12,,G V V E =。

如果1V 中每个顶点都与2V 中所有顶点邻接，则称G 为完全二部图或完全偶图(Complete Bipartite Graph)，并记为,r s K ，其中12,r V s V ==。

由定义可知，二部图是无自回路的图。

图7-55中，(),(),(),(),()a b c d e 都是二部图，其中(),(),(),()b c d e 是完全二部图1,32,32,43,3,,,K K K K 。

图7-55二部图示例显然，在完全二部图中,r s K 中，顶点数n r s =+，边数m rs =。

一个无向图如果能画成上面的样式，很容易判定它是二部图。

有些图虽然表面上不是上面的样式，但经过改画就能成为上面的样式，仍可判定它是一个二部图，如图7-56中()a 可改画成图()b ，图()c 可改画成图()d 。

可以看出，它们仍是二部图。

图7-56二部图示例定理7.5.1 无向图,G E =为二部图的充分必要条件为G 中所有回路的长度均为偶数。

证明 先证必要性。

设G 是具有互补节点子集1V 和2V 的二部图。

121(,,,,)k v v v v 是G 中任一长度为k 的回路，不妨设11v V ∈，则211m v V +∈，22m v V ∈，所以k 必为偶数，不然，不存在边1(,)k v v 。

再证充分性。

设G 是连通图，否则对G 的每个连通分支进行证明。

离散数学图论作业7-二部图匹配Problem1证明：一个无回路的简单连通图最多只有一个完美匹配。

（完美匹配指能饱和所有顶点的匹配）Problem2从下图G=(A,B,E)中，找出相对于匹配M(粗边的集合)的任意三条交错路径(alternating path)和至少两条增广路径(augmenting path)，然后利用增广路径扩大M来找到最大匹配。

a0 a1 a2 a3 a4 a5b0 b1 b2 b3 b4 b5Problem3对于哪些n值来说，下列图是存在完美匹配的二部图？a)K nb)C nc)Q n对于每一个二部图G=(A,B,E)，判断G是否有饱和A的匹配。

如果没有，请说明理由。

(1)(2)(3)(4)Problem5令k为一整数。

对于任意有限集合，证明对它的任意两个k划分都存在一个相同的代表集。

•集合的k划分指划分为大小相同的互不想交的k个子集，为简便起见，设集合的大小为k的整数倍从而每个子集均有相同个元素。

•一个划分的代表集指从每个子集中取出一个元素而构成的集合。

举例：集合{1,2,3,4}的一个2划分为A:{1,2}{3,4}。

此划分的代表集有{1,3},{2,3},{1,4},{2,4}，但{1,2}不是其代表集。

集合的另外一个划分为B:{2,3}{1,4}。

易见，A与B存在相同的代表集{1,3}。

Problem6假设某校计算机系学生选导师时出现了这样的情况：对于每一位学生，至少对k名导师感兴趣；对于每一位导师，至多有k名学生对他感兴趣。

假设每位导师只能指导1名学生，且每位学生也只能选择1名导师。

试证明：存在这样的匹配，使得每位学生都能选到自己感兴趣的导师。

证明一个6×6的方格纸板挖去左上角和右下角后不能用剪刀裁剪成若干1×2的小矩形。

基于二部图(Bipartite Network)的推荐算法不必考虑用户和项目的内容信息，它是一种结合物质扩散(Massive Diffusion)理论的推荐算法。

周涛[1]等人研究了一些物理学的知识，比如热传导理论以及物质扩散理论等，并将它们应用在推荐算法中，提出了这种基于二部图的推荐算法。

二部图是一种特殊的网络，它包含有两类不同类型节点，并且仅允许不同类型的节点之间可以有连线。

自然界许多问题可以利用二部图进行解决，比如性别关系、边着色问题等。

在二部图的应用中，同一类型节点之间的合作相互关系成为了研究领域的热点。

比如，可以利用由演员节点和演出剧目节点组成的二部图来研究演员之间在演出中的合作关系。

在一个具体的推荐系统中，可以把用户看作是一类节点，把项目看作是另一类节点。

通过由用户节点和项目节点组成的二部图，我们可以利用相邻的用户为目标用户推荐可能感兴趣的项目。

物质扩散类似于在复杂网络中的随机游走的概念。

它假设在一个系统中有着固定数量的“物质”在传递，并且在传递的过程中这些“物质”的总量始终保持守恒。

最后系统稳定状态的结果与节点的度数成正比。

在推荐系统中，我们认为目标用户所选择过的项目能够提供一定的推荐能力信息。

在操作过程中，首先为每个项目赋予初始资源1。

根据物质扩散的理论，物质的传递过程分两步走。

第一步，每个项目将自己的资源通过二部图的边均匀地分配给选择过该项目的每个用户，这样资源就从项目节点传递到了用户节点。

第二步，每个用户再将自己分配到的资源通过二部图的边平均分配给他选择过的项目，这样资源又传回到了项目节点。

虽然资源的总量在传递过程中是守恒的，但通过两次传递，每个项目所具有资源的分配状态发生了改变。

系统最后可以根据项目所拥有的资源的分布状态来计算它们之间的相似度，并确定最近邻集。

（引入具体的公式，并将改进的论文附上）文献[2]将物质扩散理论运用到了Item-based协同过滤推荐算法。

算法将选选项目的资源初始值都设为1，用稳定状态时两个项目的资源传递总量来表示它们之间的相似程度，最后利用这个相似度来计算目标用户的预测评分，并把评分较高的项目推荐给他。

二部图的匹配强迫数的开题报告一、研究背景和意义二部图匹配问题是图论中一个经典问题，它的应用非常广泛，例如在社交网络中，可以利用二部图匹配算法将人们匹配到最合适的伴侣；在作业调度中，可以将作业与合适的机器进行匹配，以实现最优的调度方案等。

在实际应用中，除了单纯的匹配问题外，还存在一些特殊的需求，例如希望匹配的结果中较为稳定，即不会随着数据的增长而发生大的变化。

而匹配的强迫数正好可以很好地解决这个问题。

二、研究内容和方法匹配强迫数（Match-forcing number）是一个二部图匹配中的概念，它定义为一个可完美匹配的子图中最小的点集合，使得将这些点从图中移除后，图不再存在完美匹配。

也就是说，这个点集合至少需要被匹配一次才能恢复完美匹配。

匹配强迫数的研究可以使得在匹配完成后进行更加稳定的分析，因此减少了应用上出现的风险。

在研究方法上，本研究主要参考了相关的论文和文章，从理论和实验两个方面进行探讨。

在理论方面，主要从图论的角度对问题进行解析，推导和证明相关结论，并且将结论和现有算法进行比较和分析。

在实验方面，本研究将使用实验数据对算法进行测试和评估，探讨其稳定性、鲁棒性和可靠性等特性，以期提出更好的算法和结果。

三、预期结果和研究意义预期结果为：（1）通过推导和证明，得到一些新的关于匹配强迫数的结论；（2）设计并实现一个高效的二部图匹配强迫数算法，并与现有算法进行比较；（3）通过大量实验数据，对算法的性能和稳定性进行评估和验证；（4）提出新的应用和解决方案，将匹配强迫数用于更广泛的问题和场景中。

研究意义为：（1）促进了对二部图匹配的研究和应用，优化了分析工具和算法，使得匹配结果更加稳定和可靠；（2）提出了一些新的关于匹配强迫数的结论并优化算法，可以推动其在实际应用中得到更加广泛的应用；（3）探讨了匹配强迫数在二部图匹配中的应用，可以拓展二部图匹配算法的实际应用场景。

平面二部图的完美匹配和分配格结构的开题报告一、研究背景图论是一门研究图与网络的学科，近年来受到越来越多的关注。

平面图是图论中的一类特殊的图，它们可以被嵌入或画成平面上。

平面图具有许多重要的性质和应用，例如欧拉定理、哈密顿路径和最小生成树等等。

平面图可以被分为二部图和非二部图。

二部图是指图中的顶点可以被划分为两个不相交的集合，且所有连接两个集合内顶点的边都不存在于同一个集合中。

平面二部图是一类特殊的二部图，其顶点和边可以被嵌入平面中，使得任意两条边没有穿过。

在平面二部图中，完美匹配和分配格结构是两个重要的概念。

完美匹配是二部图中的一个重要问题，其目的是找到一个匹配，使得所有顶点都在匹配中出现且不重复，也就是说，每个顶点只能在匹配中出现一次。

分配格结构是一个基于完美匹配的图形结构，它的目的是将二部图按照特定的规则划分为若干个格子，从而建立起一种特殊的排列方式。

二、研究内容本文主要研究平面二部图的完美匹配和分配格结构。

具体研究内容如下：1. 完美匹配的定义和性质首先介绍完美匹配的定义和性质。

针对平面二部图，讨论完美匹配的存在性和判定方法。

同时，分析完美匹配对二部图连通性的影响。

2. 分配格结构的定义和性质引入分配格结构的概念，讨论其定义和性质。

探讨分配格结构与完美匹配的关系，以及分配格结构的可计算性。

3. 完美匹配对分配格结构的影响研究完美匹配对分配格结构的影响，分析匹配与格子之间的对应关系。

同时，探讨完美匹配对分配格结构的优化作用。

4. 应用实例给出平面二部图完美匹配和分配格结构的两个应用实例。

第一个实例是一个基于电路的应用，利用完美匹配和分配格结构来优化电路布线。

第二个实例是基于组合优化的图像处理，通过完美匹配和分配格结构来实现最优的图像压缩方式。

三、研究意义本文将研究平面二部图的完美匹配和分配格结构，对深入理解平面图的结构和性质有很大的帮助。

同时，针对完美匹配和分配格结构的定义和性质，可以为后续的图论研究提供有益的参考。

关于二部图与匹配问题的探究一、二部图的基本观点二部图是一种特殊的图结构，其中的顶点可以被分为两个互不相交的集合（通常表示为U和V），集合U中的顶点与集合V中的顶点之间没有边相连。

二部图可以用数学方式表示为G=(U, V, E)，其中U和V表示两个顶点集合，E表示边的集合。

二部图的一个关键性质是，一个边的两个顶点务必分别属于两个不同的集合。

这个观点在实际中有浩繁应用，比如在婚姻匹配问题中，假设有一组男性和一组女性，我们可以用二部图来表示可能的婚姻干系。

二、匹配问题的定义与应用在二部图G=(U, V, E)中，我们称一个边的集合M为一个匹配，若果M中的边两两之间没有公共顶点。

换句话说，任意两条边都不毗连同一个顶点。

匹配问题的目标是找到一个具有最大边数的匹配M，或者找到一个最小边数的匹配。

匹配问题在实际中有浩繁应用。

例如，在网络中，我们可以将二部图中的两个顶点集合U和V分别表示为发送方和接收方，边表示毗连发送方和接收方的通信链路。

这时，匹配问题等价于如何合理分配通信链路，使得网络的容量得到最大利用。

另一个应用是在任务分配问题中。

假设有一组任务和一组工作者，每个任务需要特定的技能，每个工作者也具有特定的技能。

二部图可以用来表示任务与工作者之间的技能匹配状况。

匹配问题就变成了如何将任务分配给工作者，使得每个任务都能被合适的工作者完成。

三、匹配问题的经典算法与改进匹配问题的探究已经有了很长的历史，可以追溯到20世纪40时期。

最初，匈牙利算法是解决匹配问题最常用的算法之一。

该算法基于增广路径的观点，通过不息寻找增广路径并更新匹配，最终得到最大匹配。

然而，匈牙利算法存在一些局限性。

起首，它只能解决二部图中的最大匹配问题，不适用于其他相关问题。

其次，匈牙利算法的时间复杂度较高，不适用于大规模问题。

因此，探究者们提出了一系列改进算法，如Kuhn-Munkres算法和Hopcroft-Karp算法等。

Kuhn-Munkres算法是一种针对二部图的最大权匹配问题的改进算法。