高等固体物理4-维度

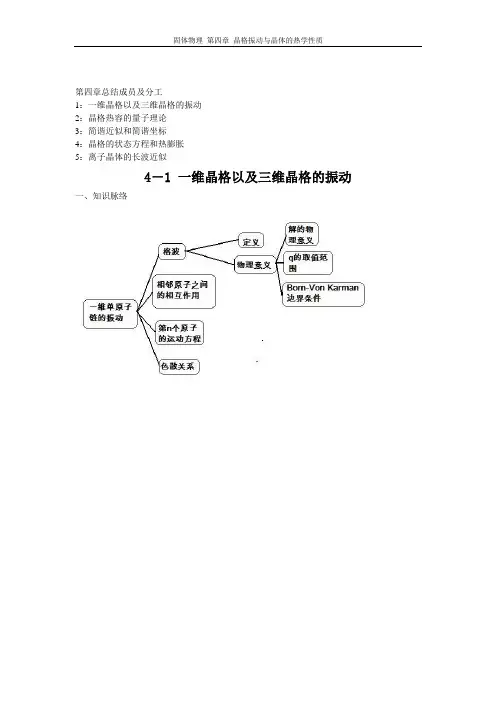
第四章总结成员及分工1：一维晶格以及三维晶格的振动2：晶格热容的量子理论3：简谐近似和简谐坐标4：晶格的状态方程和热膨胀5：离子晶体的长波近似4－1 一维晶格以及三维晶格的振动一、知识脉络二、重点1.格波的概念和“格波”解的物理意义(1)定义：晶格原子在平衡位置附近作振动时，将以前进波的形式在晶体中传播，这种波称为格波。

(2)物理意义：一个格波解表示所有原子同时做频率为ω的振动，不同原子之间有位相差。

相邻原子之间的位相差为aq 。

(3) q 的取值范围：－(π/a)<q ≤(π／a)这个范围以外的值，不能提供其它不同的波。

q 的取值及范围常称为布里渊区（Brillouin zones ）。

(4) Born-Von Karman 边界条件: 1)(=-Naq i e h Naq ⨯=π22.一维单原子链的色散关系22241[1cos ]sin ()2aq aq m m ββω=-=把 ω 与q 之间的关系称为色散关系(disperse relation)，也称为振动频谱或振动谱。

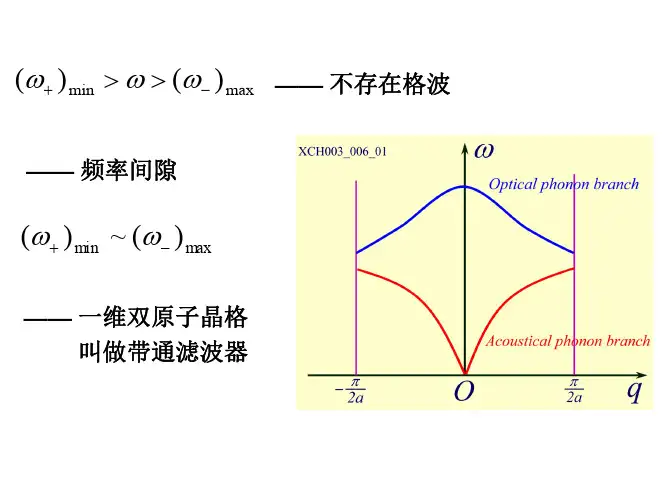
3.一维单原子链的运动方程相邻原子之间的相互作用βδδ-≈-=d dvF ad v d ⎪⎪⎭⎫ ⎝⎛=22δβ 第n 个原子的运动方程11()(2)n n n n i t naq nq m Ae ωμβμμμμ∙∙+--=+-=4.一维双原子链中两种原子的运动方程及其解（1）运动方程( equation))2(2221212n n n n M μμμβμ---=+++∙∙ )2(2221212n n n n M μμμβμ---=+++∙∙（2）方程的解(solution)])2([2q na t i n Ae -=ωμ ])12([12aq n t i n Be +-+=ωμ5.声学波与光学波的概念与物理意义（1）声学波与光学波的定义}]sin )(41[1{2/1222aq M m mM mM M m +-++=+βω }]sin )(41[1{2/1222aq M m mMmM M m +--+=-βω ω＋对应的格波称为光学波（optic wave ）或光学支（optic branch) ；ω－对应的格波称为声学波(acoustic wave)或声学支（acoustic branch ）（2）两种格波的振幅比aq m A B cos 222ββω--=⎪⎭⎫⎝⎛++aq m A B cos 222ββω--=⎪⎭⎫⎝⎛--（3）ω＋ 与ω－ 都是q 的周期函数)()(q aq --=+ωπω)()(q aq ++=+ωπω其中aq a22ππ≤〈-6.对色散关系的讨论（1）一维单原子链与一维双原子链的格波解的差异一维单原子链只有一支格波（一个波矢对应一个格波）— 声学波；而一维双原子链则有两支格波（一个波矢对应两个格波）— 声学波和光学波，两支格波的频率各有一定的范围：0)0()(min ==--ωω Maβπωω2)2()(max ==-- m aβπωω2)2()(min ==++ mMM m )(2)0()(max +==++βωω 在ω-max 与ω+min 之间有一频率间隙，说明这种频率的格波不能被激发。

four dimensions 翻译中文
四维空间是指在三维空间的基础上增加了一个附加的维度。

在物理学和数学中，四维空间通常用来描述时间的存在和运动。

四维空间可以用来解释一些现象，如相对论中的时空弯曲和宇宙的结构。

四维空间在几何学中也有应用。

它可以被用来描述一些复杂的几何形状，如四维超立方体（也称为tesseract）和四维球体。

这些形状在二维和三维空间中无法完全展示，而只能通过数学模型来描述。

在计算机图形学中，四维空间被用来进行3D动画和特效的计算。

通过在时间维度上进行变化，可以实现物体的运动和变形效果。

例如，通过在四维空间中定义一个物体的运动轨迹，可以让它在三维空间中沿着特定的路径移动。

在心理学和哲学中，四维空间也被用来思考时间的概念。

时间被认为是第四个维度，它与空间维度相互作用，影响物体的位置和状态。

通过将时间视为一个维度，我们可以更好地理解事件的顺序和发生。

四维空间是一个扩展了传统三维空间的概念，它在物理学、数学、几何学、计算机图形学以及哲学中都有广泛的应用。

通过引入额外的维度，我们可以更全面地描述物体的位置、运动和变化，以及时间的流逝。

2023年固体物理基础第三版（阎守胜著）课后题答案下载固体物理基础第三版（阎守胜著）课后答案下载第一章金属自由电子气体模型1.1 模型及基态性质1.1.1 单电子本征态和本征能量1.1.2 基态和基态的能量1.2 自由电子气体的热性质1.2.1 化学势随温度的变化1.2.2 电子比热1.3 泡利顺磁性1.4 电场中的`自由电子1.4.1 准经典模型1.4.2 电子的动力学方程1.4.3 金属的电导率1.5 光学性质1.6 霍尔效应和磁阻1.7 金属的热导率1.8 自由电子气体模型的局限性第二章晶体的结构2.1 晶格2.1.1 布拉维格子2.1.2 原胞2.1.3 配位数2.1.4 几个常见的布拉维格子2.1.5 晶向、晶面和基元的坐标2.2 对称性和布拉维格子的分类2.2.1 点群2.2.2 7个晶系2.2.3 空间群和14个布拉维格子2.2.4 单胞或惯用单胞2.2.5 二维情形2.2.6 点群对称性和晶体的物理性质 2.3 几种常见的晶体结构2.3.1 CsCl结构和立方钙钛矿结构 2.3.2 NaCl和CaF、2结构2.3.3 金刚石和闪锌矿结构2.3.4 六角密堆积结构2.3.5 实例，正交相YBa2Cu307-82.3.6 简单晶格和复式晶格2.4 倒格子2.4.1 概念的引入2.4.2 倒格子是倒易空间中的布拉维格子 2.4.3 倒格矢与晶面2.4.4 倒格子的点群对称性2.5 晶体结构的实验确定2.5.1 X射线衍射2.5.2 电子衍射和中子衍射2.5.3 扫描隧穿显微镜第三章能带论I3.1 布洛赫定理及能带3.1.1 布洛赫定理及证明3.1.2 波矢七的取值与物理意义3.1.3 能带及其图示3.2 弱周期势近似3.2.1 一维情形3.2.2 能隙和布拉格反射3.2.3 复式晶格3.3 紧束缚近似3.3.1 模型及计算3.3.2 万尼尔函数3.4 能带结构的计算3.4.1 近似方法3.4.2 n(K)的对称性3.4.3 n(K)和n的图示3.5 费米面和态密度3.5.1 高布里渊区3.5.2 费米面的构造3.5.3 态密度第四章能带论Ⅱ4.1 电子运动的半经典模型 4.1.1 模型的表述4.1.2 模型合理性的说明4.1.3 有效质量4.1.4 半经典模型的适用范围4.2 恒定电场、磁场作用下电子的运动4.2.1 恒定电场作用下的电子4.2.2 满带不导电4.2.3 近满带中的空穴4.2.4 导体、半导体和绝缘体的能带论解释 4.2.5 恒定磁场作用下电子的准经典运动 4.3 费米面的测量4.3.1 均匀磁场中的自由电子4.3.2 布洛赫电子的轨道量子化4.3.3 德哈斯一范阿尔芬效应4.3.4 回旋共振方法4.4 用光电子谱研究能带结构4.4.1 态密度分布曲线4.4.2 角分辨光电子谱测定n(K)4.5 一些金属元素的能带结构4.5.1 简单金属4.5.2 一价贵金属4.5.3 四价金属和半金属4.5.4 过渡族金属和稀土金属第五章晶格振动5.1 简谐晶体的经典运动5.1.1 简谐近似5.1.2 一维单原子链，声学支 5.1.3 一维双原子链，光学支 5.1.4 三维情形5.2 简谐晶体的量子理论5.2.1 简正坐标5.2.2 声子5.2.3 晶格比热5.2.4 声子态密度5.3 晶格振动谱的实验测定 5.3.1 中子的非弹性散射5.3.2 可见光的非弹性散射 5.4 非简谐效应5.4.1 热膨胀5.4.2 晶格热导率第六章输运现象6.1 玻尔兹曼方程6.2 电导率6.2.1 金属的直流电导率6.2.2 电子和声子的相互作用 6.2.3 电阻率随温度的变化 6.2.4 剩余电阻率6.2.5 近藤效应06.2.6 半导体的电导率6.3 热导率和热电势6.3.1 热导率6.3.2 热电势6.4 霍尔系数和磁阻第七章固体中的原子键合7.1 概述7.1.1 化学键7.1.2 晶体的分类7.1.3 晶体的结合能7.2 共价晶体7.3 离子晶体7.3.1 结合能7.3.2 离子半径7.3.3 部分离子部分共价的晶体7.4 分子晶体、金属及氢键晶体7.4.1 分子晶体7.4.2 量子晶体7.4.3 金属……第八章缺陷第九章无序第十章尺寸第十一章维度第十二章关联固体物理基础第三版（阎守胜著）：基本信息阎守胜，1938生出生，1962年毕业于北京大学物理系，现任北京大学物理学院教授，博士生导师，兼任中国物理学会《物理》杂志主编，他长期从事低温物理，低温物理实验技术，高温超导电性物理和介观物理方面的实验研究，并讲授大学生的固体物理学，低温物理学和现代固体物理学等课程。

【转载】【物理名词】06：四维时空四维设计名词解释经典物理学上的空间是三维空间。

自爱因斯坦狭义相对论以来，基于时间与空间相互纠缠的认识，将时间与空间统称为时空，时空有四个维度，其中三维为经验空间，一维为时间。

17世纪初，笛卡尔和伽利略做出了最奇异的发现：以空间为横轴、以时间为纵轴作一张图，于是穿过空间的运动成为图上的一条曲线。

在这里时间仿佛成了另一维空间，运动被冻结了，运动和变化的整个历史呈现在我们面前就像是静止不变的。

对此美国物理学家L·斯莫林认为，不应将时间转化为空间来表示。

我们知道，物质具有体积性质，没有体积的物质是不存在的，体积性质是用三维来描述的。

作为流体态物质的空间同样具有体积性质，即空间是三维的。

根据系统相对论，时间是空间的一种性质。

既然时间是空间的一种性质，那么，它就是三维空间范畴内的一个概念，而不可能独立于三维空间之外。

换言之，时间维度不能视为独立于三维空间之外的另外一维空间。

另外，观察者离不开时间，即观察者无法独立于四维时空系之外观察某个事物。

换言之，三维空间系下才存在观察者和时间。

因此，对于一个观察者来讲，四维时空系是不存在的。

可见，四维时空只是一种思维的产物，它没有任何物理意义。

语文教学：时空分析法——理解毛词的一把钥匙价量时空四维分析法时空分析法——理解毛词的一把钥匙李云东在中国古典诗词中，作家们运用充分的想象力，在写作中融入时间和空间，从而使意境和思想相融合，或伤感时间的流逝，青春的消逝，繁华的败落，或比对过往之事，暗喻眼前之心境。

或以“流水”、“落花”等物来暗喻，或以古事与今事对比呐喊抒情。

空间就更妙了，眼前之景，均是空间体现。

空间开阔，暗喻辽阔壮美之江山，细微之物，暗含纤美柔弱之柔情。

毛泽东的诗词，对空间和时间的把握，就极为高妙，赏析毛泽东的词，你会“感觉诗人是在和月亮、太阳、山川对话，整个生命都被放大了，放大到巨大的空间之后，就会感到骄傲、悲壮。

”（蒋勋）毛泽东的人格相对独立，个体生命的独立是值得称道的，体现在词中，就是一种精神的体现。

四维空间的物理学
四维空间是一个数学概念，指的是一个包含四个维度的空间，通常用来描述高维几何和物理学中的一些理论。

在物理学中，四维空间被广泛应用于相对论和量子场论等领域。

在相对论中，四维时空是描述物理事件的基本框架。

相对论将时间和空间合并成一个整体，称为时空。

时空可以被看作是一个四维的欧几里得空间，其中时间被视为第四个维度。

在相对论中，物理事件被描述为在时空中的点，这些点的坐标由四个数字组成，分别表示时间和三个空间维度上的坐标。

在量子场论中，四维空间也被广泛应用。

量子场论是描述基本粒子相互作用的理论，它将粒子视为在时空中的场。

在量子场论中，四维空间被用来描述场的传播和相互作用。

通过将场表示为四维空间中的函数，物理学家可以研究场的性质和行为。

除了相对论和量子场论，四维空间还被应用于其他物理学领域，如弦理论和宇宙学等。

在这些领域中，四维空间被用来描述物理现象和理论模型。

总的来说，四维空间是一个重要的数学概念，在物理学中有广泛的应用。

它为物理学家提供了一个描述物理现象的工具，帮助他们研究和理解自然界的基本规律。

固体物理总结绪论1研究对象及内容研究固体的结构及其组成粒子间相互作用与运动规律以阐明固态物质性能和用途的学科。

2 固体物理学发展的里程碑十八世纪：阿羽依（R. J. Ha üy 法）--坚实、相同、平行六面体的“基石”有规则重复堆积.十九世纪：布喇菲(A.Bravais法)--空间点阵学晶体周期性. 二十世纪初：X-射线衍射揭示晶体内部结构 量子理论描述晶体内部微观粒子运动过程近几十年：固体物理学→凝聚态物理：无序、尺度、维度、关联；晶体→凝聚态物质第一部分 晶体结构1 布喇菲点阵和初基矢量晶体结构的特点在于原子排列的周期性质。

布喇菲点阵是平移操作112233R n a n a n a =++所联系的诸点的列阵。

布喇菲点阵是晶体结构周期性的数学抽象。

点阵矢量112233R n a n a n a =++，其中，1n ，2n 和3n 均为整数，1a ，2a 和3a 是不在同一平面内的三个矢量，叫做布喇菲点阵的初基矢量，简称基矢。

初基矢量所构成的平行六面体是布喇菲点阵的最小重复单元。

布喇菲点阵是一个无限的分立点的列阵，无论从这个列阵中的哪个点去观察，周围点的分布和排列方位都是完全相同的。

对一个给定的布喇菲点阵，初级矢量可以有多种取法。

2 初基晶胞(原胞)初基晶胞是布喇菲点阵的最小重复单元。

初基晶胞必定正好包含布喇菲点阵的一个阵点。

对于一个给定的布喇菲点阵，初基晶胞的选取方式可以不只一种，但不论初基晶胞的形状如何，初基晶胞的体积是唯一的，()123c V a a a =⋅⨯。

3 惯用晶胞(单胞)惯用晶胞是为了反映点阵的对称性而选用的晶胞。

惯用晶胞可以是初基的或非初基的。

惯用晶胞的体积是初基晶胞体积的整数倍，c V nV =。

其中，n 是惯用晶胞所包含的阵点数。

确定惯用晶胞几何尺寸的数字叫做点阵常数。

4 维格纳-赛兹晶胞(W-S 晶胞)维格纳-赛兹晶胞是另一种能够反映晶体宏观对称性的晶胞，它是某一阵点与相邻阵点连线的中垂面(或中垂线)所围成的最小体积。

【高中物理】物理科学家利用量子霍尔效应发现“第四维度”新证据理论物理学家认为世界可能存在多达11个维度。

物理学家认为（至少在理论上），除了我们正常的三个维度外，世界可能还存在更高的维度。

第一条线索出现在1905年爱因斯坦探索狭义相对论的时候。

当然，我们一般所说的三个维度是指长度，宽度和高度。

而当我们谈论第四维的时候，这通常是指时空。

但在本文中，物理学家所指的第四维是超乎正常三维空间的空间维度。

物理学家所指的并不是一个平行宇宙，与大众科幻节目中所描述的第四维度并不相同。

即使我们宇宙或其他地方存有另一个维度，我们又与否必须前往这个一个涵盖它们的地方呢？对此，科学家也无法确认我们与否甚至可以体验至它们。

我们的大脑或许无能为力。

我们可以在数学层面叙述第四维，但我们可能将永远无法在物理范畴体验第四维。

虽说如此，这并没有阻止我们继续寻找更高维度的证据。

一个可以帮助我们更容易地理解思维的模型是：四维立方体或超立方体。

这是一个位于立方体内的立方体。

虽然是一个有用的比喻，但它并不存在于现实世界之中。

那么，科学家如何才能真正发现第四维呢？日前，两个分别位于美国和欧洲的独立研究小组已经完成了双重实验。

这两个实验都属2d，但都表明了4d世界的存有。

科学家主要就是利用了一种名叫量子霍尔效应的现象。

当电流旋转轴外磁场通过导体时，载流子出现偏移，旋转轴电流和磁场的方向可以产生一额外电场，从而在导体的两端产生电势差，这一现象就是霍尔效应。

耶鲁大学理论物理学家史蒂文格文解释量子霍尔效应霍尔效应的结果就是：电子卡在二维系统之内。

他们就可以朝两个方向移动。

量子霍尔效应出现在量子水平上，当材料处在非常低的温度时，或者就是受非常弱的磁场的影响时，量子霍尔效应就可以产生。

在这里，除了一件事情出现。

电压不是正常减少，而是逐级不升反降。

通过管制具备量子霍尔效应的电子，你同时可以测量它们。

按照数学计算，你会发现我们可以在4d系统内检测到量子霍尔效应。

固体物理思维
以下是固体物理思维的一些特点：
1. 晶体结构：固体物理思维强调对晶体结构的理解，包括原子的排列方式、晶格结构和晶体对称性等。

通过研究晶体结构，可以解释固体的物理性质和行为。

2. 能带理论：能带理论是固体物理中的重要概念，它描述了固体中电子的能量状态。

固体物理思维涉及到对能带结构、能带填充和能带隙等的理解，以解释固体的电导性、光学性质和磁性等。

3. 晶格振动：固体中的原子或离子在晶格中会进行振动，这种振动对固体的热学性质和晶格的稳定性有重要影响。

固体物理思维包括对晶格振动模式、声子和热容等的研究。

4. 晶体缺陷：晶体中可能存在各种缺陷，如点缺陷、线缺陷和面缺陷等。

固体物理思维关注这些缺陷对固体性质的影响，以及如何通过控制缺陷来改善材料的性能。

5. 量子力学：固体物理中的许多现象都需要用量子力学来解释，如电子的波粒二象性、量子态和量子隧道效应等。

固体物理思维需要掌握量子力学的基本概念和原理。

6. 实验与理论结合：固体物理思维强调实验和理论的结合。

通过实验观测和测量固体的性质，然后利用理论模型和计算来解释和预测实验结果。