逻辑学判定三段论有效性

推理结构三段论三段论推理是演绎推理中的一种简单推理判断。

他包括：一个包含大项和中项的命题（大前提）、一个包含小项和中项的命题（小前提）以及一个包含小项和大项的命题（结论）三部分。

三段论实际上是以一个一般性的原则（大前提）以及一个附属于一般性的原则的特殊化陈述（小前提），由此引申出一个符合一般性原则的特殊化陈述（结论）的过程。

三段论是人们进行数学证明、办案、科学研究等思维时，能够得到正确结论，的科学性思维方法之一。

是演绎推理中的一种正确思维的形式。

定义三段论推理是演绎推理中的一种简单推理判断。

它包含：一个一般性的原则（大前提），一个附属于前面大前提的特殊化陈述（小前提），以及由此引申出的特殊化陈述符合一般性原则的结论。

三段论推理：思维时，大脑首先用一个人为定义的内容极为明确的、囊括的范围比较大的总的原则A（简称“大前提”），再通过科学实验寻找另外一个概念小前提B，B的概念的全部内涵能够一定被包含在大前提A内、并且用文字描述的B的概念的内容时，不能人为与大前提A的内容本质完全一样（B简称小前提），然后按照小前提B如果属于大前提A 范围内，那么B的性质一定与大前提的性质一样，而得到可靠而正确的判断，此思维过程叫做正确的下结论C过程——科学术语叫做“三段论推理”。

注：由此“三段论”方法判断出的新结论，还可以成为人们下一步进行研究的新起点。

“三段论”思维，B必须有的坚实的“论据”，否则得到的结论C就可以说是错误的。

爱因斯坦的《相对论》C的得来也是依靠“三段论推理”。

凡是违背“三段论”原则的思维都是不可能得到可靠的结论。

三段论是人们进行数学证明、办案、科学研究等思维时，能够得到正确结论，的科学性思维方法之一。

是演绎推理中的一种正确思维的形式。

举例1、思维过程比喻：桌子上有碗——全家的碗一定在桌子上——红葡萄一定在碗里——红葡萄一定在桌子上，不需要开飞机满世界寻找。

图12、（如图1）生物包括所有的动物和不吃肉的动物等等，动物都属于生物A，其中，只有一部分动物吃肉，老虎属于吃肉动物（最小的圈）；所以看见新的圈被大的全包括“得出”老虎属于生物的结论。

三段论的有效式和推理形式一、引言三段论是一种重要的推理方法，在逻辑学和哲学中被广泛应用。

它由三个命题组成，包括一个前提、一个中间命题和一个结论。

三段论推理有不同的有效式和推理形式，本文将深入探讨这些内容。

二、三段论的基本结构三段论的基本结构由三个命题组成，它们可以是陈述句、条件句或假设句。

这三个命题分别被称为前提（major premise）、中间命题（minor premise）和结论（conclusion）。

2.1 前提前提是三段论的第一个命题，也是推理的基础。

它包含一般性的信息，是在推理中用来支持结论的命题。

2.2 中间命题中间命题是三段论的第二个命题，它连接前提和结论。

中间命题通常是一个特殊性质或例子，它通过与前提进行对比或对比来支持结论。

2.3 结论结论是三段论的最后一个命题，它是根据前提和中间命题得出的结论。

结论是推理的结果，它应该是从前提和中间命题推导出来的合理结论。

三、三段论的有效式三段论有几种有效式，其中最常见的是AAA式、EAE式、AEE式和EIO式。

3.1 AAA式AAA式是最简单的三段论有效式，其中所有的命题都是陈述句，且都是肯定命题。

例如：1.所有A都是B。

2.所有B都是C。

3.所有A都是C。

AAA式的有效性在于，当前提和中间命题都是真时，结论必定是真的。

3.2 EAE式EAE式是一种三段论有效式，其中所有的命题都是陈述句，且都是否定命题。

例如：1.没有A是B。

2.所有B都不是C。

3.没有A是C。

EAE式的有效性在于，当前提和中间命题都是真时，结论必定是真的。

3.3 AEE式AEE式是一种三段论有效式，其中前提是陈述句，中间命题是假设句，结论是陈述句。

例如：1.所有A都是B。

2.没有B是C。

3.没有A是C。

AEE式的有效性在于，当前提和中间命题都是真时，结论必定是真的。

3.4 EIO式EIO式是一种三段论有效式，其中前提是假设句，中间命题是陈述句，结论是否定命题。

例如：1.没有A是B。

三段论格的证明范文三段论是一种基本的推理形式，可以通过推理论证来证明其有效性。

以下是一个超过1200字的三段论证明的示例：三段论是一种基本的推理形式，由一个前提（主前提）和一个中间前提组成，通过推理得出一个结论。

它是逻辑学中的一种重要推理规则，广泛应用于各个领域的推理和论证中。

在这个证明中，我们将证明三段论的有效性。

首先，我们来定义三段论的三个组成部分：主前提、中间前提和结论。

主前提是一个普遍真理的陈述，中间前提是一个特殊情况的陈述，结论是由主前提和中间前提推导出的结论。

在三段论中，结论被认为是有效的，如果它可以通过主前提和中间前提的逻辑关系得出。

接下来，我们将使用一个具体的例子来证明三段论的有效性。

假设主前提是：“所有人类都是动物”，中间前提是：“约翰是人类”，那么结论就是：“约翰是动物”。

首先，根据主前提，“所有人类都是动物”，我们可以得出约翰是动物的推论。

这是因为约翰是人类，而人类是动物，所以约翰是动物。

这个推理是合乎逻辑的，因为它符合主前提中的普遍真理。

其次，再次看一下中间前提，“约翰是人类”。

根据这个陈述，我们可以得出约翰是动物的结论。

这是因为约翰属于人类这个特殊情况，而人类是动物，所以约翰是动物。

这个推理也是合乎逻辑的，因为它符合中间前提中的特殊情况。

通过以上两个推理，我们可以得出结论：“约翰是动物”。

这个结论是有效的，因为它是通过主前提和中间前提推导出来的。

这个推理符合逻辑，且在任意情况下都是有效的。

因此，通过上述例子，我们证明了三段论的有效性。

三段论是一种基本的推理形式，广泛应用于各个领域的推理和论证中。

它能够通过主前提和中间前提推导出有效的结论，因此在逻辑学中具有重要的地位。

总结起来，三段论是逻辑学中的一种基本推理形式。

它由主前提、中间前提和结论组成，通过逻辑推理得出一个有效的结论。

我们通过一个具体的例子证明了三段论的有效性。

三段论在各个领域的推理和论证中都有广泛的应用，它是逻辑思维和推理的重要工具。

三段论的无效式
三段论是逻辑学中常用的推理方式，但是有些情况下，三段论并不一定是有效的。

下面介绍三种常见的三段论无效式。

1. 假设前提无法成立
如果前提是错误的或者无法成立，那么三段论就是无效的。

例如：所有人都是魔法师。

汤姆是人。

因此，汤姆是魔法师。

这个推理显然是无效的，因为前提“所有人都是魔法师”是错误的。

2. 中间项没有联系
如果中间项与其他两个命题无法建立联系，那么三段论就是无效的。

例如：
所有狗都有尾巴。

所有鸟都有翅膀。

因此，狗和鸟有共同点。

这个推理是无效的，因为中间项“狗和鸟”与前提中的其他两项没有联系。

3. 两个前提之间没有联系
如果两个前提之间没有联系，那么三段论就是无效的。

例如：
所有人都需要呼吸氧气。

石头不需要呼吸氧气。

因此，石头不是人。

这个推理是无效的，因为两个前提之间没有联系，无法推导出结论。

总之，虽然三段论是一种常用的推理方式，但是需要注意前提的正确性和三个命题之间的联系，才能确保推理的有效性。

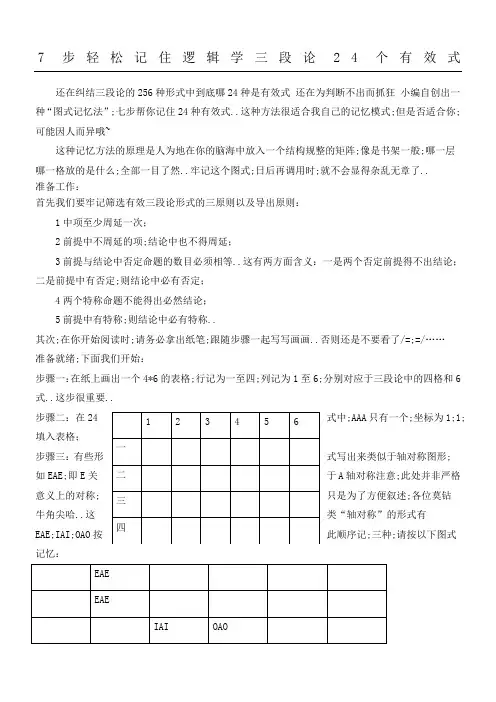
7步轻松记住逻辑学三段论24个有效式还在纠结三段论的256种形式中到底哪24种是有效式还在为判断不出而抓狂小编自创出一种“图式记忆法”;七步帮你记住24种有效式..这种方法很适合我自己的记忆模式;但是否适合你;可能因人而异哦~这种记忆方法的原理是人为地在你的脑海中放入一个结构规整的矩阵;像是书架一般;哪一层哪一格放的是什么;全部一目了然..牢记这个图式;日后再调用时;就不会显得杂乱无章了..准备工作：首先我们要牢记筛选有效三段论形式的三原则以及导出原则：1中项至少周延一次；2前提中不周延的项;结论中也不得周延；3前提与结论中否定命题的数目必须相等..这有两方面含义：一是两个否定前提得不出结论；二是前提中有否定;则结论中必有否定；4两个特称命题不能得出必然结论；5前提中有特称;则结论中必有特称..其次;在你开始阅读时;请务必拿出纸笔;跟随步骤一起写写画画..否则还是不要看了/=;=/……准备就绪;下面我们开始：步骤一：在纸上画出一个4*6的表格;行记为一至四;列记为1至6;分别对应于三段论中的四格和6式..这步很重要..步骤二：在24式中;AAA只有一个;坐标为1;1;填入表格；步骤三：有些形式写出来类似于轴对称图形;如EAE;即E关于A轴对称注意;此处并非严格意义上的对称;只是为了方便叙述;各位莫钻牛角尖哈..这类“轴对称”的形式有EAE;IAI;OAO按此顺序记;三种;请按以下图式记忆：注：联想记忆：在对当关系矩阵中;E命题是处于I命题上一层的;因此此处EAE处于IAI上一层..仅适用于此步骤..步骤四：如果我们把三段论的每个形式的三个字母;如EAE;分为左、中、右三部分的话;那么：左边两个相同的只有AAI;它分布于表格的1、2、4行;即一、二、四格;第三格是无意义的；此步骤仅需要文字记忆;请自行把AAI填入第一步画好的表格中..建议坐标：1;33.14;1步骤五：同理;右边两字母相同的有AII;AEE;AOO按顺序记;请按照下列图式记忆：步骤六：有两种形式是四格通用的;即EAO;EIO;请按照下列图式记忆：基础图形：对当关系方阵步骤七：经过上面六个步骤;我们已经写出了1+5+3+5+8=22个形式;剩下的只剩一种形式：AEO;填入最后两个空;即第二格和第四格空缺位置即可..如此一来;24个形式便都记下来了..在最后考试时;先把这个表格写在草稿纸上;再去根据表格里的形式做题;就清晰很多..像是中学时考数学先把公式都写到草稿纸上是同一个道理..另外需要说明的是;记住这个表格只是基础;还需要配合你自己从表格里总结出来的各种规律;最后考试时才能百战不殆..。

三段论推论和结论在逻辑学中，三段论是一种常见的推理形式，由前提、推理规则和结论三部分组成。

其中，前提是作为推理基础的陈述，推理规则是用来推导出结论的逻辑规则，而结论则是通过前提和推理规则得出的推论。

三段论在日常生活中得到广泛应用，可以帮助我们进行合理的推理和论证。

三段论的推论过程是基于逻辑规则的。

在三段论中，推理规则是一种逻辑原则，用来从前提出发推导出结论。

常见的推理规则有假言推理、附言推理、假设推理等。

这些推理规则可以帮助我们根据已知的前提得出合理的结论。

例如，如果已知“A是B，B是C”，那么根据假言推理的推理规则，我们可以得出“A是C”的结论。

这种推理过程是基于逻辑的，可以使我们的思考更加准确和合理。

三段论的推论过程需要具备有效的前提。

前提是推理的基础，是推导结论的依据。

只有当前提是真实和有效的时候，才能得出正确的结论。

因此，在进行三段论推论时，我们需要确保前提的准确性和可靠性。

如果前提存在错误或者不完整，那么得出的结论也就会失去可靠性。

因此，在进行推论时，我们需要对前提进行仔细的分析和评估，确保它们的有效性。

三段论的结论需要根据前提和推理规则得出。

结论是推论的最终结果，是通过前提和推理规则得出的逻辑推理。

一个有效的结论应该是与前提和推理规则相吻合的，能够合理地解释前提中的信息。

在得出结论之前，我们需要对前提进行分析，并根据推理规则进行推导。

只有在推理过程正确无误的情况下，才能得出准确的结论。

总的来说，三段论是一种常见的推理形式，可以帮助我们进行合理的推理和论证。

它的推论过程是基于逻辑规则的，需要具备有效的前提，并根据前提和推理规则得出结论。

三段论的应用范围广泛，可以用于日常生活中的思考和论证，也可以应用于学术研究和科学推理中。

通过运用三段论的推论和结论，我们可以提高思维的逻辑性和合理性，从而做出更准确和科学的判断。

在逻辑学领域，三段论概念最早由亚里士多德提出，在今天仍然是传统逻辑和现代逻辑的重要组成部分；在法学领域，司法三段论是西方近代法治理想所凝结的法律推理模式，是大陆法系司法判决推理的主要形式。

逻辑三段论（为区别司法三段论，本文把逻辑学中的三段论称为“逻辑三段论”。

下同）与司法三段论可谓既有联系，又有区别。

正确地理解和把握二者的关系，对于合理地分析司法三段论，客观地认识逻辑学在法律实践和法律研究中的作用，具有十分重要的意义。

一、已有认识的不足在逻辑科学中，三段论概念具有确定的含义和所指。

由包含一个共同项的两个直言命题出发得到一个新的直言命题的演绎推理，即直言三段论是最基本和最典型的表现形式。

如：所有的人都是要死的，（大前提）苏格拉底是人，（小前提）所以，他也是要死的。

（结论）形如（A →B ）∧(B →C)→(A →C)的推理，即假言连锁推理，因为B 的媒介作用类似于直言三段论中的中项，因此也称假言三段论。

此外，连锁三段论、关系三段论、模态三段论等也都是三段论的表现形式。

诸多三段论类型中，惟有直言三段论常被简称为三段论，其他类型的三段论不能作此省略。

在法律领域，对“三段论”这一名词人们也并不陌生，长期以来它都被看作是大陆法系司法判决推理的主要形式，称为司法三段论。

通常被描述为：法律规则（大前提）案件事实（小前提）裁决（结论）从逻辑三段论与司法三段论的结构来看，二者无疑都由大前提、小前提和结论三部分组成。

但这并不意味着，后者所涉及的推理模式就等同于前者。

正是在这一问题上，部分法学者的描述较为混乱。

例如，有学者指出，在“以事实为根据，以法律为准绳”的审判原则指导下，法官将法律规则适用于具体案件事实得出判决的逻辑推论过程，遵循如下推理模式：T →R S=T S →R该推理属于何种类型？答曰：“它是形式逻辑的一个公式，叫形式逻辑的三段论。

一个严格的逻辑三段论公式第一段：T →R ，叫大前提，第二段：S=T ，叫小前提，第三段：S →R ，是得出的推论。

三段论的逻辑框架引言三段论是一种重要的逻辑推理方式，它由古希腊哲学家亚里士多德提出并系统化。

三段论由三个命题组成，包括前提（premise）和结论（conclusion），它们之间通过中项（middle term）进行推理。

三段论以其简洁、准确的形式在逻辑学和思维训练中广泛应用，有助于分析和推导。

三段论的结构三段论由三个命题构成，其中包括两个前提命题和一个结论命题。

下面是三段论的基本结构：1.前提1：Major Premise（大前提）：包含一个普遍命题，它揭示了一般情况或规律。

2.前提2：Minor Premise（小前提）：包含一个特殊命题，它是对大前提中普遍概念的具体应用。

3.结论：Conclusion（结论）：通过前提1和前提2之间的中项进行推理得出的结论。

三段论的逻辑框架可以用以下形式表示：1. 所有 A 是 B。

2. C 是 A。

3. 因此，C 是 B。

其中，A是中项，B是大前提的谓词（predicate），C是小前提的主词（subject）。

通过前提1和前提2之间的中项A，我们可以推导出结论C是B。

三段论的推理方式三段论的推理方式有三种，包括：1.全三段论：当前提1和前提2都为真时，结论也必然为真。

例如：“所有人都会死亡。

约翰是人。

因此，约翰会死亡。

”2.部分三段论：当前提1为真时，结论有可能为真。

例如：“所有鸟都会飞翔。

企鹅是鸟。

因此，企鹅会飞翔。

”在这个例子中，结论并不一定成立，因为并非所有鸟都会飞翔。

3.无效三段论：当前提1和前提2都为真时，结论却不一定为真。

例如：“所有狗都有四条腿。

这只猫有四条腿。

因此，这只猫是狗。

”在这个例子中，结论并不成立，因为并非所有有四条腿的动物都是狗。

三段论的应用三段论可以帮助我们进行逻辑分析和推理。

通过正确地应用三段论，我们可以从已知信息中推导出新的结论，从而更好地理解和解决问题。

在科学、哲学、法律、数学等领域中，三段论被广泛应用于论证和推理过程中。

直言三段论是所有前提都是直言命题的演绎推理。

所有动物都终有一死。

所有人都是动物。

所以，所有人都终有一死。

前两个命题叫做前提。

如果这个三段论是有效的，这两个前提逻辑上蕴涵了最后的命题，它叫做结论。

结论的真实性建立在前提的真实性和它们之间的联系之上：中项在前提中必须周延（distribute）至少一次，形成在结论中的主词和谓词之间的连接。

即使直言三段论是有效的，但如果有前提为假的话结论仍可能是假。

命题可以是全称的（universal）或特称的（particular），并且可以是肯定的或否定的。

所以有四种命题:A型：全称肯定的- “所有S都是P”，简写为SaP。

I型：特称肯定的- “有些S是P”，简写为SiP。

E型：全称否定的- “没有S是P”，简写为SeP。

O型：特称否定的- “有些S不是P”，简写为SoP。

在下列这个三段论中:下面讨论直言三段论的格。

先识别三种不同类型的项：大项、小项和中项。

作为结论中的谓词出现的项是大项。

在上述三段论中的P是大项。

小项是作为结论中的主词出现的项；此间S是小项。

通过排除法可知，中项是没有出现在结论中，却在每个前提中都出现一次的项；此间M是中项。

大项所在的前提叫大前提，小项所在的前提叫小前提。

直言三段论的格经由识别中项的四种可能排列而得到。

格用数字来表示：第1格第2格第3格第4格大前提M-P P-M M-P P-M小前提S-M S-M M-S M-S结论S-P S-P S-P S-P四个格之间可相互转换：第1格：不需转换。

第2格：对换大前提的前后两项的位置就变成第1格，对换小前提的前后两项的位置就变成第4格。

第3格：对换大前提的前后两项的位置就变成第4格，对换小前提的前后两项的位置就变成第1格。

第4格：对换大前提的前后两项的位置就变成第3格，对换小前提的前后两项的位置就变成第2格。

E和I命题对换前后两项的位置而保持同原命题等价。

A命题不能对换前后两项的位置，但可以在前项确实有元素存在的前提下，转换成与弱于原命题的I命题。