下载文档原格式
高斯-克吕格投影与UTM投影高斯-克吕格(Gauss-Kruger)投影与UTM投影（Universal Transverse Mercator，通用横轴墨卡托投影）都是横轴墨卡托投影的变种，目前一些国外的软件或国外进口仪器的配套软件往往不支持高斯-克吕格投影，但支持UTM投影，因此常有把UTM投影当作高斯-克吕格投影的现象。
从投影几何方式看，高斯-克吕格投影是“等角横切圆柱投影”，投影后中央经线保持长度不变，即比例系数为1；UTM投影是“等角横轴割圆柱投影”，圆柱割地球于南纬80度、北纬84度两条等高圈，投影后两条割线上没有变形，中央经线上长度比0.9996。
从计算结果看，两者主要差别在比例因子上，高斯-克吕格投影中央经线上的比例系数为1， UTM投影为0.9996，高斯-克吕格投影与UTM投影可近似采用 X[UTM]=0.9996 * X[高斯]，Y[UTM]=0.9996 * Y[高斯]，进行坐标转换（注意：如坐标纵轴西移了500000米，转换时必须将Y 值减去500000乘上比例因子后再加500000）。
从分带方式看，两者的分带起点不同，高斯-克吕格投影自0度子午线起每隔经差6度自西向东分带，第1带的中央经度为3°；UTM投影自西经180°起每隔经差6度自西向东分带，第1带的中央经度为-177°，因此高斯-克吕格投影的第1带是UTM的第31带。
此外，两投影的东伪偏移都是500公里，高斯-克吕格投影北伪偏移为零，UTM北半球投影北伪偏移为零，南半球则为10000公里。
高斯-克吕格投影与UTM投影坐标系高斯- 克吕格投影与UTM投影是按分带方法各自进行投影，故各带坐标成独立系统。
以中央经线（L0）投影为纵轴X，赤道投影为横轴Y，两轴交点即为各带的坐标原点。
为了避免横坐标出现负值，高斯- 克吕格投影与UTM北半球投影中规定将坐标纵轴西移500公里当作起始轴，而UTM南半球投影除了将纵轴西移500公里外，横轴南移10000公里。
地球椭球体(Ellipsoid)、大地基准面(Datum)及地图投影(Projection)三者的基本概念地球椭球体(Ellipsoid)众所周知我们的地球表面是一个凸凹不平的表面，而对于地球测量而言，地表是一个无法用数学公式表达的曲面，这样的曲面不能作为测量和制图的基准面。
假想一个扁率极小的椭圆，绕大地球体短轴旋转所形成的规则椭球体称之为地球椭球体。
地球椭球体表面是一个规则的数学表面，可以用数学公式表达，所以在测量和制图中就用它替代地球的自然表面。
因此就有了地球椭球体的概念。
地球椭球体有长半径和短半径之分，长半径(a)即赤道半径，短半径(b)即极半径。
f=（a-b）/a为椭球体的扁率，表示椭球体的扁平程度。
由此可见，地球椭球体的形状和大小取决于a、b、f 。
因此，a、b、f被称为地球椭球体的三要素。
对地球椭球体而言，其围绕旋转的轴叫地轴。
地轴的北端称为地球的北极，南端称为南极；过地心与地轴垂直的平面与椭球面的交线是一个圆，这就是地球的赤道；过英国格林威治天文台旧址和地轴的平面与椭球面的交线称为本初子午线。
以地球的北极、南极、赤道和本初子午线等作为基本要素，即可构成地球椭球面的地理坐标系统(A geographic coordinate system (GCS) uses a threedimensional spherical surface to define locations on the earth.A GCS includes an angular unit of measure, a prime meridian,and a datum (based on a spheroid).)。
可以看出地理坐标系统是球面坐标系统，以经度/维度（通常以十进制度或度分秒(DMS)的形式）来表示地面点位的位置。
地理坐标系统以本初子午线为基准（向东，向西各分了1800）之东为东经其值为正，之西为西经其值为负；以赤道为基准（向南、向北各分了900）之北为北纬其值为正，之南为南纬其值为负。
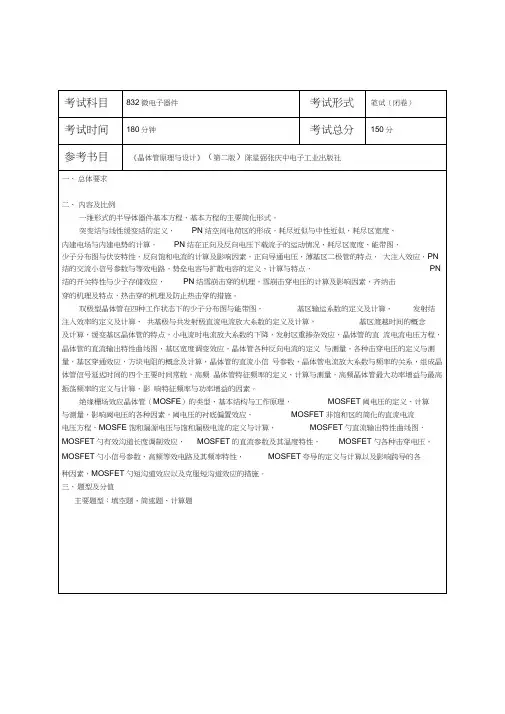
（3）测量结果的置信度2.3 除方法 2.4 2.5 均 2.6 合成 2.7 系统误差的判断及消除方法粗大误差的判断及剔除方法 等精度测量和不等精度测量 误差的合成（1）误差传递公式 （1）定义、特征、分类（2）发现方法、判据（3）削弱或消 （1）判别准则（2）剔除方法 （1）等精度测量结果的数据处理（2）不等精度测量的加权平 （2）各种函数关系（和差、积商、乘方开方、指数对数）的 2）分类（3）评定方法（4）合成 测量不确定度（1）基本概念（ 测量数据处理（1）有效数字及舍入处理（2）测量数据的表示方法（3）最小二乘法的基本 2.8 原理 3、时间与频率的测量 3.1时间与频率的测量原理 （1）模拟测量技术（ 3.2电子计数器的组成原理和主要测量功能 （1）3.3电子计数器的测量误差分析 （1）测频误差（ 较，中界频率 高分辨率时间和频率测量技术 （1）多周期同步测量技术（2）模拟内插法（3）游标法 微波频率测量技术 （1）变频法（2）置换法 频率稳定度测量的基本概念 （1）频率稳定度的表征（2）频稳的时域定义，阿仑方差的测 2）数字测量技术 测频（2）测周（3）测频比（4）测时间间隔 2）测周误差（3）测频和测周土 1误差的比 3.43.5 3.6 量。
3.7 调制域测量技术 （1）调制域测量的基本概念（2）无间歇计数器的实现 4、电压测量4.1交流电压的测量 （1）峰值、均值、有效值的 AC/DC 转换的原理（2）峰值电压表、均值电 压表及有效值电压表的刻度特性及误差分析（ 4.2直流电压的数字测量技术 （1） 斜式、三斜式等A/D 转换原理 4.3数字多用表（DMIM 及其变换技术 的组成特点及使用 4.4 DVM 的误差分析及自动化技术 部件的误差（4） DVM 勺自动校正技术（ 4.5电压测量的干扰及其抑制技术 措施（3）共模干扰的误差分析及抑制措施 5、信号波形测量（信号时域测量）5.1波形显示器件 CRT 结构及波形显示原理 （1） CRT 的组成及基本性能参数（2）光点扫描式 波形显示原理（3）扫描与同步（4）连续扫描和触发扫描 5.2波形模拟显示技术和通用示波器 （1）通用示波器的组成（2） Y （垂直）通道及其主要性 能（3） X （水平）通道的组成、触发电路、扫描发生器环的原理（ 4）多波形显示技术，双踪和双时 基显示原理 5.3波形取样技术及取样示波器 参数。
高斯-克吕格投影与UTM投影高斯-克吕格(Gauss-Kruger)投影与UTM投影（Universal Transverse Mercator，通用横轴墨卡托投影）都是横轴墨卡托投影的变种，目前一些国外的软件或国外进口仪器的配套软件往往不支持高斯-克吕格投影，但支持UTM投影，因此常有把UTM投影当作高斯-克吕格投影的现象。
从投影几何方式看，高斯-克吕格投影是“等角横切圆柱投影”，投影后中央经线保持长度不变，即比例系数为1；UTM投影是“等角横轴割圆柱投影”，圆柱割地球于南纬80度、北纬84度两条等高圈，投影后两条割线上没有变形，中央经线上长度比0.9996。
从计算结果看，两者主要差别在比例因子上，高斯-克吕格投影中央经线上的比例系数为1， UTM投影为0.9996，高斯-克吕格投影与UTM投影可近似采用 X[UTM]=0.9996 * X[高斯]，Y[UTM]=0.9996 * Y[高斯]，进行坐标转换（注意：如坐标纵轴西移了500000米，转换时必须将Y 值减去500000乘上比例因子后再加500000）。
从分带方式看，两者的分带起点不同，高斯-克吕格投影自0度子午线起每隔经差6度自西向东分带，第1带的中央经度为3°；UTM投影自西经180°起每隔经差6度自西向东分带，第1带的中央经度为-177°，因此高斯-克吕格投影的第1带是UTM的第31带。
此外，两投影的东伪偏移都是500公里，高斯-克吕格投影北伪偏移为零，UTM北半球投影北伪偏移为零，南半球则为10000公里。
高斯-克吕格投影与UTM投影坐标系高斯- 克吕格投影与UTM投影是按分带方法各自进行投影，故各带坐标成独立系统。
以中央经线（L0）投影为纵轴X，赤道投影为横轴Y，两轴交点即为各带的坐标原点。
为了避免横坐标出现负值，高斯- 克吕格投影与UTM北半球投影中规定将坐标纵轴西移500公里当作起始轴，而UTM南半球投影除了将纵轴西移500公里外，横轴南移10000公里。
3.2地球椭球体基本要素
3.2.1地球椭球体
我们称大地水准面包围形成的形体为大地球体。
由于地球体内部物质分布的不均匀，导致重力方向的变化，因此与重力方向成正交的大地水准面也是不规则的，仍不能利用数学方法表达。
大地水准面的形状虽然十分复杂，但从整体上看，起伏是微小的，它是一个接近绕自转轴（短轴）旋转的椭球体。
所以，在测量和制图中就用旋转椭球体来代替大地球体，这个旋转球体通常称为地球椭球体，简称椭球体。
地球椭球体表面是一个规则的数学表面。
椭球体的大小通常用两个半径：长半径a和短半径b或者由一个半径和扁率来决定。
扁率α表示椭球的扁平程度，扁率的计算公式为：α=（a-b）/a。
这些地球椭球体的基本元素a、b和α等，由于推求它的年代、使用的方法以及测定的地区不同，其结果并不一致，故地球椭球体的参数值有很多种，现将世界常用的地球椭球体的参数值列于表3-1。
表3-1各种地球椭球体模型的参数值
椭球体名称年代长半轴（m）短半轴（m）扁率
埃维尔斯特（Everest）1830 6377276 6356075 1：300.8
贝赛尔（Bessel）1841 6377397 6356079 1：299.15
克拉克（Clarke）1866 6378206 6356584 1：295.0
克拉克（Clarke）1880 6378249 6356515 1：293.5
海福特（Hayford）1910 6378388 6356912 1：297
克拉索夫斯基1940 6378245 6356863 1：298.3
I.U.G.G 1967 6378160 6356775 1：298.25
中国在1952年以前采用海福特椭球体，从1953—1980年采用克
拉索夫斯基椭球体。
随着人造地球卫星的发射，有了更精密的测算地球形体的仪器。
1975年第16届国际大地测量及地球物理联合会上通过国际大地测量协会第一号决议中公布的地球椭球体称为GRS （1975），中国自1980年开始采用GRS（1975）新参考椭球体系。
由于地球椭球长半径与短半径的差值很小，所以当制作小比例尺地图时，往往把它当作球体看待，这个球体的半径为6371km。
3.2.2地图比例尺
地图比例尺是指地图上某线段的长与相应的实地水平距离之比，即地图比例尺=图上长度/相应实地水平距离。
例如一幅地图的比例尺是1:50000，则图上两点间为1cm时，实地两点间的距离为50000cm。
根据地图的目的和要求不同，地图比例尺也有大小之分。
分母小则比值大，比例尺也就大；分母大则比值小，比例尺就小。
地图比例尺常以图形结合文字、数字表示下面将分别说明。
1）数字比例尺
数字比例尺就是简单的分数或比例，可表示为1:1000000或
1/1000000，最好用前者。
这意味着，在地图上（沿特定线）的长度1mm、1cm或1英寸（分子），代表在地球表面上的1000000mm、1000000cm或1000000英寸（分母）。
2）文字比例尺
文字比例尺就是描述图上距离与实地距离之间的关系。
例如，1:1000000这一数字比例尺可描述为“图上1mm等于实地lkm”。
3）图解比例尺或直线比例尺
图解比例尺或直线比例尺是在地图上绘出的直线段，常常绘于图例方框中或图廓下方，表示图上长度相当于实地距离的单位。
4）面积比例尺
面积比例尺是图上面积与实地面积之比，表示图上1单位面积（平方厘米）与实地同一种平方单位的特定数量之比。
3.2.3高程
高程（Elevation）是指某点沿铅垂线方向到基准面的距离，是测绘用词，俗称海拔高度。
如图3-2所示，P0P0’；为大地水准面，地面点A和点B到P0P0’的垂直距离H A和H B分别为A、B两点的高度。
地面点到任一水准面的高程称为相对高程。
在图3-2中，A、B两点至任一水准面的垂直距离和P1P1’即为H A’、H B’即为A、B两点的相对高程。
本文摘自：
《地理信息系统原理与实践》，吴秀芹主编，清华大学出版社，2011.11 ISBN：978-7-302-26238-1。
