圆锥的投影、截交线及轴侧图
- 格式:ppt
- 大小:3.74 MB
- 文档页数:21

中职——机械制图课件第五章第六章第五章轴测投影学习要点:主要学习绘制轴测图的基本方法,对发展空间思维和想象能力会有很大的促进。
案例导入:将物体连同其参考直角坐标系一起,沿不平行于任一坐标平面的方向,用平行投影法将其投影在单一投影面上所得到的图形,称为轴测投影图,简称为抽测图(如图5-1)。
1.轴间角在4-1中,轴测轴之间的夹角∠X1O1Y1、∠Y1O1Z1、∠X1O1Z1称为轴间角。
2.轴向伸图缩系数轴测轴上的单位长度与相应直角坐标轴上的单位长度的比值轴向伸图缩系数。
在空间三坐标轴上,分别取长度OA、OB、OC,它们的轴测投影长度为O1A1、O1B1、O1C1,令p=,q=,r=,则p、q、r分别称为OX、OY、OZ轴的轴向伸缩系数。
轴测投影按如前所述,分为正轴测投影和斜轴测投影。
每类再根据轴向伸缩系数的不同又分为三种:正(或斜)等轴测图p1=q1=r1正(或斜)二轴测图p1=r1≠q1正(或斜)三轴测图p1≠r1≠q1在轴测投影中,工程上应用最广泛的是正等测和斜二测。
如图5-2为长度均为a的正方体的两种轴测图。
在轴测投影中,工程上应用最广泛的是正等测和斜二测。
如图5-2为长度均为a的正方体的两种轴测图。
轴测投影的基本性质1.物体上相互平行的线段的轴测投影仍相互平行;2.物体上平行于坐标轴的直线段的轴测投影仍与相应的轴测轴平行;3.物体上两平行线段或同一直线上的两线段长度之比,其轴测投影保持不变。
正等测的三个轴间角相等,如图5-3∠X1O1Y1=∠Y1O1Z1=∠X1O1Z1=120°正等测的轴向伸缩系数也相等p1=q1=r1=0.82为了作图方便,一般采用简化轴向伸缩系数,p=q=r,即凡平行于各坐标轴的尺寸都按原尺寸作图。
形体的直观形象没有影响。
轴间角:∠X1O1Y1=∠Y1O1Z1=∠X1O1Z1=120°轴向变形系数:p=q=r=0.82简化轴向变形系数:p=q=r=11.平面立体正等轴测图的画法(1)在视图上建立坐标系;(2)画出正等测轴测轴;(3)按坐标关系画出物体的轴测图。

形体的表面交线圆锥的截交线掌握圆锥截交线的分析方法;掌握圆锥截交线的求解步骤。
目的和要求圆锥的截交线圆锥面的截交线因截平面与锥轴的相对位置不同,截交线可以是圆、椭圆、抛物线、双曲线或相交二直线。
平面与圆锥面交线的轴测图、投影图和截交线的形状如下。
垂直于轴线与素线都相交平行于一条素线平行于两条素线过锥顶截平面位置θ=0°θ<αθ=αθ>α截交线形状圆椭圆抛物线双曲线相交二直线轴测图投影图圆锥的截交线曲面立体截交线的特殊点:1.极限点 确定曲线范围的最高、最低、最前、最后、最左和最右点。
2.转向点 曲线上处于曲面投影转向线上的点,它们是区分曲线可见与不可见部分的分界点。
3.特征点 曲线本身具有特征的点,如椭圆长短轴上四个端点。
4.结合点 截交线由几部分不同线段(曲线、直线)组成时结合处的那些点。
对于特殊点,根据现有的知识凡是能求出来的都应求出来。
圆锥的截交线圆锥面的截交线因截平面与锥轴的相对位置不同,截交线可以是圆、椭圆、抛物线、双曲线或相交二直线。
平面与圆锥面交线的轴测图、投影图和截交线的形状如下。
垂直于轴线与素线都相交平行于一条素线平行于两条素线过锥顶截平面位置θ=0°θ<αθ=αθ>α截交线形状圆椭圆抛物线双曲线相交二直线轴测图投影图圆锥的截交线例1. 求圆锥截切后的投影。
作图步骤:1.空间分析、投影分析;2.求出所有的特殊点;3.补画若干一般位置点;4.光滑连线,并判别可见性;5.整理轮廓线。
圆锥的截交线例2. 求圆锥截切后的投影。
作图步骤:1.空间分析、投影分析;2.求出所有的特殊点;3.补画若干一般位置点;4.光滑连线,并判别可见性;5.整理轮廓线。
课 程 小 结1. 圆锥截交线的三种情况——圆、椭圆、抛物线、 双曲线、三角形;2. 圆锥截交线的作图步骤:(1)空间分析、投影分析;(2)求出所有的特殊点;(3)补画若干一般位置点;(4)光滑连线,并判别可见性;(5)整理轮廓线。

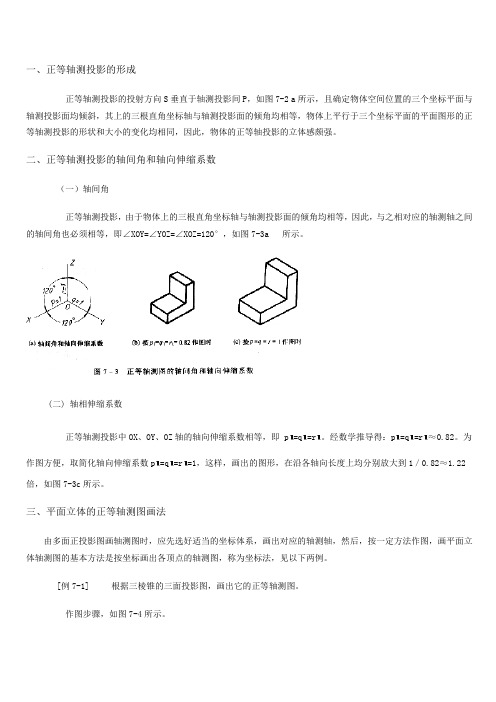
一、正等轴测投影的形成正等轴测投影的投射方向S垂直于轴测投影间P,如图7-2 a所示,且确定物体空间位置的三个坐标平面与轴测投影面均倾斜,其上的三根直角坐标轴与轴测投影面的倾角均相等,物体上平行于三个坐标平面的平面图形的正等轴测投影的形状和大小的变化均相同,因此,物体的正等轴投影的立体感颇强。
二、正等轴测投影的轴间角和轴向伸缩系数(一)轴间角正等轴测投影,由于物体上的三根直角坐标轴与轴测投影面的倾角均相等,因此,与之相对应的轴测轴之间的轴间角也必须相等,即∠XOY=∠YOZ=∠XOZ=120°,如图7-3a 所示。
(二) 轴相伸缩系数正等轴测投影中OX、OY、OZ轴的轴向伸缩系数相等,即 p=q=r。
经数学推导得:p=q=r≈0.82。
为作图方便,取简化轴向伸缩系数p=q=r=1,这样,画出的图形,在沿各轴向长度上均分别放大到1/0.82≈1.22倍,如图7-3c所示。
三、平面立体的正等轴测图画法由多面正投影图画轴测图时,应先选好适当的坐标体系,画出对应的轴测轴,然后,按一定方法作图,画平面立体轴测图的基本方法是按坐标画出各顶点的轴测图,称为坐标法,见以下两例。
[例7-1] 根据三棱锥的三面投影图,画出它的正等轴测图。
作图步骤,如图7-4所示。
[例7-2] 根据六棱柱的三面投影图,画出它的正等轴测图。
作图步骤,如图7-5所示。
本题关键在于选定坐标轴和坐标圆点,如先确定顶面各点的坐标,可避免画不必要的作图线。
四、曲面立体的正等轴测图的画法(一)坐标平面(或其平面)上的圆的正等轴测投影坐标平面(或其平行面)上圆的正等轴测投影为椭圆。
立方体平行于坐标平面的各表面上的内切圆的正等轴测投影,如图7-6所示。
从图7-6中可以看出:(1)分别平行于坐标平面的圆的正等轴测投影均为形状和大小完全相同的椭圆,但其长轴和短轴方向各不相同。
(2)各椭圆的长轴方向垂直于不属于轴测投影(即轴测轴),且在菱形(圆的外切正方形的轴测投影)的长对角线上;短轴方向平行于不属于此坐标平面的那根坐标轴的轴测投影(即轴测轴),且在菱形的短对角线上。


单元四基本体及其截断体的投影项目描述:任何机体,不管其形状多么复杂,都可以看成是由圆柱、圆锥、圆球、棱柱、棱锥等单一几何形体(基本体)按一定方式组合而成,它们是构成形体的基本单元。
本项目中通过介绍各种基本几何体及截断体的投影特征,学习基本几何体的画法及表面取点方法;学习基本几何体及截断体尺寸标注方法。
项目目标:1、掌握平面立体和曲面立体的种类及其三视图画法。
2、掌握平面立体和圆柱体表面取点、取线的作图方法。
3、能正确、完整的标注基本及其切口穿孔的尺寸。
4、掌握截切基本体交线的画法。
能力目标:1、学会运用投影原理分析基本体及其三视图。
2、培养运用投影原理绘制基本体三视图的能力。
3、掌握基本几何体表面求点方法。
任务一平面立体根据表面性质的不同,基本体分为平面立体和曲面立体两类。
立体表面全部由平面所围成的立体,称为平面立体。
如棱柱和棱锥等。
图4-1 基本体组成的机体一、六棱柱三视图及斜截六棱柱的三视图画法棱柱由两个底面和棱面组成,棱面与棱面的交线称为棱线,棱线互相平行。
棱线与底面垂直的棱柱称为正棱柱。
图4-2a所示为一正六棱柱。
由上、下两个底面(正六边形)和六个棱面(长方形)组成。
设将其放置成上、下底面与水平投影面平行,并有两个棱面平行于正投影面面。
(a) (b) 立体图 (c)投影图图4-2 正六棱柱投影及表面上的点的三视图1.六棱柱的三视图分析上、下两底面均为水平面,它们的水平投影重合并反映实形,正面及侧面投影积聚为两条相互平行的直线。
六个棱面中的前、后两个为正平面,它们的正面投影反映实形,水平投影及侧面投影积聚为一直线。
其他四个棱面均为铅垂面,其水平投影均积聚为直线,正面投影和侧面投影均为类似形。
(1)俯视图六棱柱的俯视图是正六边形,是六棱柱顶面和底面的重合投影,反映顶、底面的实形。
正六边形的六条边是六个侧面垂直于顶、底面的积聚性投影。
(2)主视图六棱柱的主视图由三个矩形线框组成。
中间的矩形线框为前、后侧面的重合投影,反映实形。