高一数学必修一和四期末测试模拟题

人教版高一数学必修1必修4期末测试卷附答案人教版高一数学必修1必修4期末测试卷姓名：__________ 班级：___________ 学号：____________ 分数：______________一、选择题（每题5分，共40分）1.集合A={x∈N*｜-1<x<3}的子集的个数是（。

）。

A。

4.B。

8.C。

16.D。

322.函数f(x)=1/(1-x)+lg(1+x)的定义域是（。

）。

A。

(-∞,-1)。

B。

(1,+∞)。

C。

(-1,1)U(1,+∞)。

D。

(-∞,+∞)3.设a=log2,c=5-1/3,b=ln22，则（。

）。

A。

a<b<c。

B。

b<c<a。

C。

c<a<b。

D。

c<b<a4.函数y=-x^2+4x+5的单调增区间是（。

）。

A。

(-∞,2]。

B。

[-1,2]。

C。

[2,+∞)。

D。

[2,5]5.已知函数f(x)=x^2-2ax+3在区间(-2,2)上为增函数，则a的取值范围是（。

）。

A。

a≤2.B。

-2≤a≤2.C。

a≤-2.D。

a≥26.下列函数中，既是偶函数，又在区间(0,+∞)上单调递减的函数是（。

）。

A。

y=x-2.B。

y=x-1.C。

y=x^2.D。

y=x^37.若函数f(x)=x/(2x+1)(x-a)为奇函数，则a=（。

）。

A。

1/2.B。

2/3.C。

3/4.D。

1/88.已知α是第四象限角，XXX(π-α)=5/12，则sinα=（。

）。

A。

1/5.B。

-1/5.C。

5.D。

-59.若tanα=3，则sinαcosα=（。

）。

A。

3.B。

3/2.C。

3/4.D。

9/410.sin600°的值为（。

）。

A。

3/2.B。

-3/2.C。

-1/2.D。

1/211.已知cosα=3/5，π/4<α<π，则XXX(α+π/4)=（。

）。

A。

1.B。

-1.C。

5/8.D。

-5/812.在△ABC中，sin(A+B)=sin(A-B)，则△ABC一定是（。

高一数学上册必修一、必修四期末测试卷高一数学三新班期末测试注意事项：1.考试范围为必修一和必修XXX的三角函数及三角恒等变换。

2.本试卷共有选择题、填空题和解答题三种题型，共计16个小题。

3.考试建议用时为60分钟+10分钟（附加题），满分100分。

一、选择题（共8个小题，每小题5分，共40分）1.如果集合U={1,2,3,4,5,6,7,8}，A={2,5,8}，B={1,3,5,7}，那么A∩B的值为（）。

A、{5}B、{1,3,7}C、{2,8}D、{1,2,3,5,7,8}2.设函数f(x)=1/(1+x)-x，则f(x)的表达式为（）。

A、1/(1-x)B、1/(1+x)C、1-xD、1+x/(1-x)3.函数y=1-x/(1+x)是（）。

A、奇函数B、偶函数C、既是奇函数又是偶函数D、非奇非偶函数4.已知f(x)=x-ax+bx+2，且f(-5)=17，则f(5)的值为（）。

A、-13B、13C、-19D、195.若f(x)=-x+2ax与g(x)=2a/(x+1)在区间[1,2]上都是减函数，则a的值范围是（）。

A、(-1,)∪(,1)B、(-1,)∪(,1]C、（，1）D、(,1]6.三个数0.76，60.7，log0.7(6)的大小关系为（）。

A、60.7<0.76<log0.7(6)B、0.7<log0.7(6)<60.76<60.7C、log0.7(6)<0.76<60.7D、0.7<0.76<60.7<log0.7(6)7.已知α是第四象限的角，则cos(α-2π/5)=（）。

A、-sin4π/5B、-sin8π/5C、±cos4π/5D、±cos8π/58.已知sin(π+α)=2/5，且α是第四象限的角，则cos(α-2π/5)=（）。

A、-3/5B、-4/5C、3/5D、4/5二、填空题（共4个小题，每小题5分，共20分）9.函数y=log1/(3x-2)的定义域是（）。

高一数学（必修一，必修四）期末练习题一．A 卷1．0390sin 的值为（ ） A.23 B.23- C.21- D.21 2．若sin 0α<，tan 0α>，则角α的终边在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．函数x x x f cos sin 2)(=是 ( ) A ．最小正周期为2π的奇函数 B ．最小正周期为2π的偶函数 C ．最小正周期为π的奇函数D ．最小正周期为π的偶函数4．设M 和m 分别是函数1)62cos(31--=πx y 的最大值和最小值，则M+m 等于（ ）A.32B.32-C. 34- D.2-5．已知角α的终边经过点)3,1(P ，则α2cos 的值为 ( ) A. 21-B. 23-C . 21 D. 236. tan(40)-，tan38，tan56的大小关系是（ ）A ．tan(40)tan 38tan 56->>B ．tan 56tan 38tan(40)>>-C ．tan 38tan(40)tan 56>->D ．tan 56tan(40)tan 38>->7．将函数sin 2y x =的图象向左平移6π个单位，所得图象的函数解析式为（ ） A ．sin 26y x π⎛⎫=+⎪⎝⎭C ．sin 26y x π⎛⎫=-⎪⎝⎭B ．sin 23y x π⎛⎫=+⎪⎝⎭D ．sin 23y x π⎛⎫=-⎪⎝⎭8．在ABC ∆中，若135cos ,53cos ==B A ，则C sin 的值为（ ）A. 6556-B. 6556C. 6563D.6516-9．为了得到函数)32sin(π-=x y 的图象，只需把函数x y 2sin =的图象 ( )A. 向左平移3π个长度单位 B. 向右平移3π个长度单位C. 向左平移6π个长度单位 D. 向右平移6π个长度单位 10．对于函数)62sin(2π+=x y ，则下列结论正确的是 ( )A .)(x f 的图象关于点)0,3(π对称 B.)(x f 在区间]6,3[ππ-递增C .)(x f 的图象关于直线12π-=x 对称 D. 最小正周期是2π11.105sin 15cos 75cos 15sin +=12. 已知扇形的半径为2，圆心角是3π弧度，则该扇形的面积是 . 13. 函数x x y 2cos 2sin =的最小正周期是 ，最大值是 。

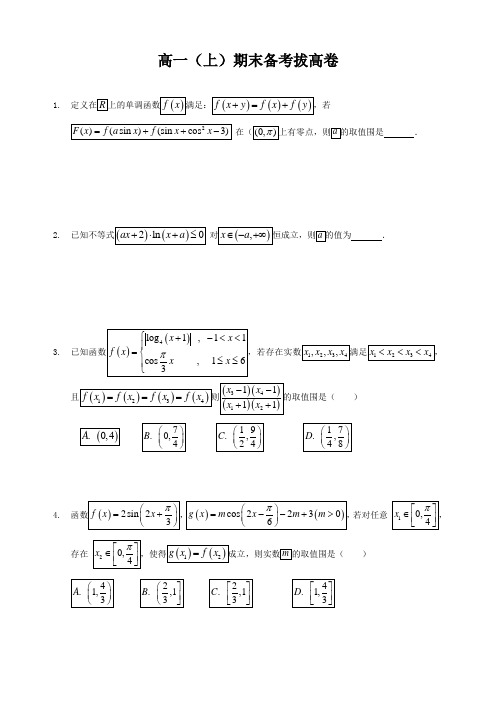
高一（上）期末备考拔高卷1.的取值围是．2.的值为．3.）4.若对任意存在）5. 函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示． （Ⅰ）求函数()f x 的解析式；（Ⅱ）若函数()2321212F x fx mf x ππ⎡⎤⎛⎫⎛⎫=-+-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦在区间0,2π⎡⎤⎢⎥⎣⎦上有四个不同零点，数m 的取值围．6. 已知二次函数()2f x ax bx c =++．（1）若0a c =>，()11f =，对任意 []2,2x ∈-，()f x 的最大值与最小值之和为()g a ，求()g a 的表达式；（2）若,,a b c 为正整数，函数()f x 在11,44⎛⎫- ⎪⎝⎭上有两个不同零点，求a b c ++的最小值．7. 已知函数()()224f x x x a a a a R =-+-∈．（Ⅰ）当1a =-时，求()f x 在[]3,0-上的最大值和最小值； （Ⅱ）若方程()0f x =有3个不相等的实根123,,x x x ，求123111x x x ++的取值围．参考答案1.的取值围是．∴f（asinx）+f（sinx+cos2x﹣3）=0在（0，π）上有解；2.的值为．【解析】∴当1a x a -<<- 时，()ln 0y x a =+<， 当1x a >-时，()ln 0y x a =+>，又()()2ln 0ax x a +⋅+≤对(),x a ∈-+∞恒成立，① 若0a >，2y ax =+与()ln y x a =+均为定义域上的增函数， 在(),x a ∈-+∞上，可均大于0，不满足题意；② 若0a =，则2ln 0x ≤对()0,x ∈+∞不恒成立，不满足题意； ∴0a <． 作图如下：由图可知，当且仅当方程为()ln y x a =+的曲线与方程为2y ax =+的直线相交于点A ，即满足()20ln 0ax x a +=⎧⎪⎨+=⎪⎩时，()()2ln 0ax x a +⋅+≤对(),x a ∈-+∞恒成立，解方程()20ln 0ax x a +=⎧⎪⎨+=⎪⎩得21x a x a⎧=-⎪⎨⎪=-⎩，解得1a =-．故答案为：﹣1．3. 已知函数()()4log 1 , 11cos , 163x x f x x x π⎧+-<<⎪=⎨≤≤⎪⎩，若存在实数1234,,,x x x x 满足1234x x x x <<<，且()()()()1234f x f x f x f x===则()()()()34121111x xx x--++的取值围是（）(). 0,4A7. 0,4B⎛⎫⎪⎝⎭19. ,24C⎛⎫⎪⎝⎭17. ,48D⎛⎫⎪⎝⎭【解析】题意，可得12331012x x x-<<<<<<，4962x<<，则()()4142log1log1x x+=+，即为()()4142log1=log1x x-++，可得()()12111x x++=，由cos3y xπ=的图象关于直线3x=对称，可得346x x+=，则()()()()()()2343433312115653411x xx x x x xx x--=-=--=--+++在31,2⎛⎫⎪⎝⎭递增，即有()()()()34121111x xx x--++的取值围是（0，）．故选B．4.函数()2sin23f x xπ⎛⎫=+⎪⎝⎭，()()cos22306g x m x m mπ⎛⎫=--+>⎪⎝⎭，若对任意10,4xπ⎡⎤∈⎢⎥⎣⎦，存在20,4xπ⎡⎤∈⎢⎥⎣⎦，使得()()12g x f x=成立，则实数m的取值围是（）4. 1,3A⎛⎫⎪⎝⎭2. ,13B⎛⎤⎥⎝⎦2. ,13C⎡⎤⎢⎥⎣⎦4. 1,3D⎡⎤⎢⎥⎣⎦【解析】解：当x∈[0，]时，2x+∈[，]，sin（2x+）∈[，1]，f （x ）=2sin （2x +）∈[1，2]，同理可得2x ﹣∈[﹣，]，cos （2x ﹣）∈[，1]，g （x ）=mcos （2x ﹣）﹣2m +3∈[﹣+3，﹣m +3]，对任意x 1∈[0，]，存在x 2∈[0，]，使得g （x 1）=f （x 2）成立，∴，求得1≤m ≤，故选：D ．5. 函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示． （Ⅰ）求函数()f x 的解析式；（Ⅱ）若函数()2321212F x fx mf x ππ⎡⎤⎛⎫⎛⎫=-+-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦在区间0,2π⎡⎤⎢⎥⎣⎦上有四个不同零点，数m 的取值围．【解析】（Ⅰ）根据f （x ）=Asin （ωx +φ）的部分图象知，A=1，=﹣=，∴T=π，∴ω==2；由“五点法画图”知，2×+φ=，解得φ=；∴函数f （x ）=sin （2x +）；（Ⅱ）∵f （x ﹣）=sin （2x ﹣+）=sin2x ，∴函数F （x ）=3[f （x ﹣）]2+mf （x ﹣）+2=3sin 2（2x ）+msin2x +2；在区间[0，]上有四个不同零点，设t=sin2x ，由x ∈[0，]，得2x ∈[0，π]，即sin2x ∈[0，1]， ∴t ∈[0，1]，令F （x ）=0，则3t 2+mt +2=0在[0，1]上有两个不等的实数根， 令g （t ）=3t 2+mt +2则由，解得﹣5＜m ＜﹣2； ∴实数m 的取值围是﹣5＜m ＜﹣2．6. 已知二次函数()2f x ax bx c =++．（1）若0a c =>，()11f =，对任意 []2,2x ∈-，()f x 的最大值与最小值之和为()g a ，求()g a 的表达式；（2）若,,a b c 为正整数，函数()f x 在11,44⎛⎫-⎪⎝⎭上有两个不同零点，求a b c ++的最小值． 【解析】（1）a=c ＞0，f （1）=1，则a +b +a=1，b=1﹣2a ，∴f （x ））=ax 2+（1﹣2a ）x +a=a +，当1﹣≤﹣2，即0＜a ≤时，g （a ）=f （﹣2）+f （2）=10a ；当﹣2＜1﹣≤0，即＜a ≤时，g （a ）=f （1﹣）+f （2）=a ﹣+3，当a ＞时，g （a ）=f （1﹣）+f （﹣2）=9a ﹣﹣1，综上所述，g （a ）=；（2）函数f （x ）在（﹣，）上有两个不同零点x 1，x 2，则x 1+x 2=﹣＜0，＞x 1x 2=＞∴a ＞16c ，由根的分布可知f （﹣）=a ﹣b +c ＞0，即a +16c ＞4b ，∵a ，b ，c 为正整数，∴a +16c ≥4b +1 f （0）=c ＞0，△＞0，b ，∴a +16c ＞8+1，可得（）2＞1，∵a ＞16c ，∴＞1， ∴，∴a ＞25，∴a ≥26， ∴b≥，∴b ≥11，c ≥1． f （x ）=26x 2+11x +1，经检验符合题意，故a +b +c 的最小值为38．7. 已知函数()()224f x x x a a a a R =-+-∈．（Ⅰ）当1a =-时，求()f x 在[]3,0-上的最大值和最小值； （Ⅱ）若方程()0f x =有3个不相等的实根123,,x x x ，求123111x x x ++的取值围． 【解答】（Ⅰ）∵，∴=，x∈[﹣2，0]时，4≤f（x）≤5，x∈[﹣3，﹣2]时，2≤f（x）≤5，∴f（x）min=f（﹣3）=2，f（x）max=f（0）=5；（Ⅱ）∵f（x）=，①若a＞0，∵方程f（x）=0有3个不相等的实根，故x＜2a时，方程f（x）=﹣x2+2ax+a2﹣4a=0有2个不相等的实根，x≥2a时，方程f（x）=x2﹣2ax+a2﹣4a=0有1个不相等的实根，∴，解得：2＜a＜4，不妨设x1＜x2＜x3，则x1+x2=2a，x1x2=﹣a2+4a，x3=a+2，∴++=+=﹣＞，∴++的围是（，+∞），②若a＜0，当x＞2a时，方程f（x）=x2﹣2ax+a2﹣4a=0的判别式小于0，不符合题意；③a=0时，显然不和题意，故++的围是（，+∞）．。

人教版高一数学必修1必修4期末测试卷姓名____________班级___________学号____________分数______________一、选择题（每题5分，共40分）1 ．集合A ＝{x ∈N ﹡｜－1<x<3)的子集的个数是（ ）A ．4B ．8C ．16D ．322 ．函数1()lg(1)1f x x x =++-的定义域是（ ）A ．(,1)-∞-B ．(1,)+∞C ．(1,1)(1,)-+∞ D ．(,)-∞+∞3 ．设2135,2ln ,2log -===c b a,则（ ）A ．c b a <<B ．a c b <<C ．b a c <<D ．a b c <<4 ．函数245y x x =-++（ ）A ．(],2-∞B ．[]1,2-C ．[)2,+∞D ．[]2,55 ．已知函数2()23f x x ax =-+在区间()2,2-上为增函数,则a 的取值范围是 （）A ．2a ≤B ．22a -≤≤C ．2a ≤-D 2a ≥6 ．下列函数中,既是偶函数,又在区间(0,)+∞上单调递减的函数是 （ ）A ．2y x -=B ．1y x -=C ．2y x =D ．13y x =7 ．若函数))(12()(a x x xx f -+=为奇函数,则a =（ ）A ．21 B ．32 C ．43 D ．18 ．已知α是第四象限角,5tan()12πα-=,则sin α= （ ）A ．15B ．15-C ．513D ．513-9 ．若tan 3α=,则sin cos αα=（ ）A ．32 B 3C ．33D ．3410．sin600︒的值为（ ）A 3B ．3C ．12-D ．1211．已知3cos 5α=,0πα<<,则πtan()4α+=（ ）A ．15 B ．-1 C ．17D ．7-12．在ABC ∆中,sin(A+B)=sin(A-B),则ABC ∆一定是（ ）A ．等腰三角形B ．等边三角形C ．直角三角形D ．锐角三角形二、填空题（每题5分，共30分） 13．函数y =的定义域为______________.14．用二分法求方程x 3-2x-5=0在区间[2,3]上的近似解,取区间中点x 0=2.5,那么下一个有解区间为_____________.15．若圆心角是2弧度的扇形的弧长是cm 15,则扇形的面积是______________ 16．若3cos 5α=-,且3(,)2παπ∈,则tan α=___________________ 三、解答题（每题10分，共30分） 17．已知α为锐角,且tan()24πα+=.(Ⅰ)求tan α的值; (Ⅱ)求sin 2cos sin cos 2αααα-的值.18．已知函数2()sin 22sin f x x x =-(I)求函数()f x 的最小正周期.(II)求函数()f x 的最大值及()f x 取最大值时x 的集合.19．已知:()132sin cos 322+-+=x x x f ()R x ∈.求:(Ⅰ)()x f 的最小正周期; (Ⅱ)()x f 的单调增区间;(Ⅲ)若x ∈[4π-,4π]时,求()x f 的值域. 20．求函数)46tan(3xy -=π的周期及单调区间．21．已知||2,||3,a b a ==与b 的夹角为120°｡(I)求()()23a b a b -⋅+的值;(II)当x 为何值时,xa b -与3a b +垂直｡22．已知向量)3,cos 2(2x a =→-,)2sin ,1(x b =→-,函数→-→-⋅=b a x f )(,(Ⅰ)求函数)x (f 的最小正周期和值域;(Ⅱ)在∆ABC 中,c b a ,,分别是角C B A ,,的对边,且3)(=C f ,1=c ,32=ab ,且b a >,求b a ,的值。

2019-2020学年高一数学上册期末模拟卷（3）参考答案与试题解析一．选择题（共12小题，每小题5分，共60分）1．（2019秋•鲁山县校级月考）已知集合A＝{x|x2﹣3x+2＝0}，B＝{x|0＜x＜6，x∈N}，则满足A⊆C⊆B的集合C的个数为（）A．4B．8C．7D．16【解析】解：集合A＝{x|x2﹣3x+2＝0}＝{1，2}，B＝{x|0＜x＜6，x∈N}＝{1，2，3，4，5}，∴满足A⊆C⊆B的集合C有：{1，2}，{1，2，3}，{1，2，4}，{1，2，5}，{1，2，3，4}，{1，2，3，5}，{1，2，4，5}，{1，2，3，4，5}，共8个．故选：B．【点睛】本题考查满足条件的集合的个数的求法，是基础题，解题时要认真审题，注意子集定义、列举法的合理运用．2．（2020•攀枝花一模）函数f（x）＝的部分图象大致是（）A．B．C．D．【解析】解：因为f（﹣x）＝＝﹣f（x），所以函数f（x）为奇函数，图象关于原点对称，排除D，又当x小于0趋近于0时，f（x）＜0，故排除B，又f（﹣π）＝＝＞0，据此排除C．故选：A．【点睛】本题考查了函数的图象及其变换．属中档题．3．（2019秋•常州期中）已知函数y＝f（x），y＝g（x），两者的定义域都是I，若对于任意x∈I，存在x0，使得f（x）≥f（x0），g（x）≥g（x0），且f（x0）＝g（x0），则称f（x），g（x）为“兄弟函数”，已知函数f（x）＝x2+2px+q（p，q∈R），是定义在区间上的“兄弟函数”那么函数f（x）在区间的最大值为（）A．3B．C．D．13【解析】解：∵＝，（当且仅当x＝，即x＝2时，等号成立）．∴g（x）在x＝2处取得最小值3；又∵f（x）与g（x）是定义在区间[，3]上的“兄弟函数”，∴f（x）在x＝2处取得最小值3；∴f（x）＝x2+px+q＝（x﹣2）2+3．∴函数f（x）在区间的最大值为f（）＝．故选：C．【点睛】本题考查函数的最值，考查新定义，考查函数的单调性，考查学生的计算能力，属于中档题．4．（2019秋•荆州区校级月考）已知定义在R上的函数f（x）满足对任意x∈R都有f（1+x）+f（1﹣x）＝0成立，且函数f（x+1）的图象关于直线x＝﹣1对称，则f（2019）＝（）A．0B．2C．﹣2D．﹣1【解析】解：∵函数f（x+1）的图象关于直线x＝﹣1对称，∴函数f（x）的图象关于y轴对称，∴f（x）＝f（﹣x），又f（1+x）+f（1﹣x）＝0，∴f[1+（x+1）]+f[1﹣（x+1）]＝0即f（x+2）+f（﹣x）＝0，∴f（x+2）＝﹣f（﹣x）＝﹣f（x），∴f[（x+2）+2]＝﹣f（x+2）＝f（x）即f（x+4）＝f（x），∴函数f（x）的一个周期T＝4，∵f（1+x）+f（1﹣x）＝0，当x＝0时有f（1）＝0，则f（﹣1）＝0，f（3）＝0．∴f（2019）＝f（4×504+3）＝f（3）＝0．故选：A．【点睛】本题主要考查函数周期的求解，根据条件推导f（x+T）＝f（x）的形式是解决本题的关键．另可借助图象法快速求解．5．（2019秋•上城区校级月考）设函数f（x）的定义域为R，满足，且当x∈（0，1]时，f（x）＝x（x﹣1）．若对任意x∈[m，+∞），都有，则m的最小值是（）A．B．C．D．【解析】解：∵，∴f（x）＝2f（x+1）当x∈（0，1]时，f（x）＝x（x﹣1）∈[，0]，x∈（﹣1，0]时，x+1∈（0，1]，f（x）＝2f（x+1）＝2（x+1）x∈[，0]，x∈（﹣2，﹣1]时，x+1∈（﹣1，0]，f（x）＝2f（x+1）＝4（x+2）（x+1）∈[﹣1，0]，将函数大致图象在数值上画出，如图x∈（﹣2，﹣1]时，令4（x+2）（x+1）＝﹣，解得：x1＝，x2＝﹣，若对任意x∈[m，+∞），都有f（x）≥﹣，所以m≥﹣，故选：A．【点睛】考查二次函数图象的平移，由，得f（x）＝2f（x+1），即每次向左移动一个单位，函数值域缩小一倍，利画出图形，用数形结合求解．6．（2020•天河区一模）已知x1＝1n，x2＝e，x3满足e＝lnx3，则下列各选项正确的是（）A．x1＜x3＜x2B．x1＜x2＜x3C．x2＜x1＜x3D．x3＜x1＜x2【解析】解：依题意，因为y＝lnx为（0，+∞）上的增函数，所以x1＝1n＜ln1＝0；因为y＝e x为R上的增函数，且e x＞0，所以0＜x2＝e，＜e0＝1；x3满足e＝lnx3，所以x3＞0，所以＞0，所以lnx3＞0＝ln1，又因为y＝lnx为（0，+∞）的增函数，所以x3＞1，综上：x1＜x2＜x3．故选：B．【点睛】本题考查了指数函数，对数函数的单调性，函数值的大小比较等，属于中档题．7．（2019秋•泸州月考）已知函数f（x）＝log3x的图象与函数g（x）的图象关于直线y＝x对称，函数h （x）是最小正周期为2的偶函数，且当x∈[0，1]时，h（x）＝g（x）﹣1，若函数y＝k•f（x）+h（x）有3个零点，则实数k的取值范围是（）A．（1，2log73）B．（﹣2，﹣2log53）C．（﹣2log53，﹣1）D．（﹣log73，﹣）【解析】解：由函数f（x）＝log3x的图象与函数g（x）的图象关于直线y＝x对称，得g（x）＝3x，函数h（x）是最小正周期为2的偶函数，当x∈[0，1]时，h（x）＝g（x）﹣1＝3x﹣1，函数y＝k•f（x）+h（x）有3个零点，即k log3x＝﹣h（x）有3个不同根，画出函数y＝k log3x与y＝﹣h（x）的图象如图：要使函数y＝k log3x与y＝﹣h（x）的图象有3个交点，则k＜0，且，即﹣2＜k＜﹣2log53．∴实数k的取值范围是（﹣2，﹣2log53）．故选：B．【点睛】本题考查函数零点与方程根的关系，考查数形结合的解题思想方法与数学转化思想方法，是中档题．8．（2019秋•天河区校级月考）黄金三角形有两种，其中底和腰之比为黄金分割比的黄金三角形被认为是最美的三角形，它是顶角为36°的等腰三角形（另一种是顶角为108°的等腰三角形），例如，正五角星由5个黄金三角形和一个正五边形组成，如图所示，在一个黄金三角形ABC中，，根据这些信息，可得sin234°＝（）A．B．C．﹣D．﹣【解析】解：由图可知，∠ACB＝72°，且cos72°＝＝．∴cos144°＝2cos272°﹣1＝﹣．则sin234°＝sin（144°+90°）＝cos144°＝﹣．故选：C．【点睛】本题考查三角函数的恒等变换，考查解读信息与应用信息的能力，是中档题．9．（2019秋•黄州区校级月考）将函数的图象向右平移个单位，得到函数g（x）的图象，则下列说法不正确的是（）A．B．g（x）在区间上单调递减C．是g（x）图象的一条对称轴D．是g（x）图象的一个对称中心【解析】解：将函数f（x）＝sin（2x﹣）的图象向右平移个单位长度，得到函数y＝g（x）＝sin[2（x﹣）﹣]＝sin（2x﹣），对于A，g（）＝sin（2×﹣）＝sin＝1，正确；对于B，令2kπ+≤2x﹣≤2kπ+，k∈Z，解得：kπ+≤x≤kπ+，k∈Z，可得函数在[，]单调递减，由＜，可得g（x）在区间上单调递减，正确；对于C，由于g（﹣）＝sin[2×（﹣）﹣]＝sin（﹣）＝﹣1，故正确；对于D，由于g（）＝sin（2×﹣）＝sin（﹣）≠0，故错误；故选：D．【点睛】本题主要考查了三角函数的图象和性质，三角函数图象的平移，考查了逻辑推理能力和运算求解能力．10．（2019秋•天津期中）已知菱形ABCD的边长为2，∠BAD＝120°，点E，F分别在边BC，DC 上，，．则＝（）A．B．C．D．【解析】解：根据题意，分别以直线AC，BD为x，y轴，建立如图所示平面直角坐标系，根据菱形ABCD的边长为2，∠BAD＝120°可求出以下几点的坐标：B，C（1，0），，∵，，∴，∴，，∴，∴．故选：A．【点睛】本题考查了通过建立坐标系，利用坐标解决向量问题的方法，根据点的坐标可求向量的坐标，中点坐标和定比分点坐标公式，向量数量积的坐标运算，考查了计算能力，属于中档题．11．（2019春•聊城期末）已知sin（α﹣β）＝，sin2β＝，α，β，则α+β＝（）A．B．C．或D．或【解析】解：sin2β＝，β，即2β∈[，π]，可得cos2β＝﹣＝﹣，sin（α﹣β）＝，α，β，即有α﹣β∈[，]，即α﹣β∈[，π]，cos（α﹣β）＝﹣＝﹣，由α+β＝α﹣β+2β∈[π，2π]，cos（α+β）＝cos[（α﹣β）+2β]＝cos（α﹣β）cos2β﹣sin（α﹣β）sin2β＝﹣•（﹣）﹣•＝，可得α+β＝．故选：B．【点睛】本题考查三角函数的和差公式，考查同角的平方关系，以及角的变换，考查运算能力，属于中档题．12．（2019•烟台二模）已知函数y＝f（x）的定义域为R，f（x+1）为偶函数，且对∀x1＜x2≤1，满足，若f（3）＝1，则不等式f（log2x）＜1的解集为（）A．（，8）B．（1，8）C．（0，）∪（8，+∞）D．（﹣∞，1）∪（8，+∞）【解析】解：∵f（x+1）为R上的偶函数，∴f（﹣x+1）＝f（x+1），∴函数f（x）关于直线x＝1对称．对∀x1＜x2≤1，满足＜0，等价于∀x1＜x2≤1，f（x2）＜f（x1），即函数f（x）在x≤1时，函数f（x）单调递减．若f（3）＝1，则不等式f（log2x）＜1⇔f（log2x）＜f（3）．∴3＞log2x＞﹣1，解得：8．∴不等式f（log2x）＜1的解集为．故选：A．【点睛】本题考查了究函数的单调性奇偶性、方程与不等式的解法、等价转化方法，考查了推理能力与计算能力，属于难题．二．填空题（共4小题，每小题5分，共20分）13．（2019春•越城区校级月考）二次函数f（x）＝ax2+bx+c，且a+b+c＝1，则max{a，b，c}的最小值为（max{a，b，c}表示a，b，c中的最大数）．【解析】解：令t＝min{a，b}，求t的max．由a，c的对称性，不妨假设c≥a，即2a+b≤1，则t＝min{a，b}由b2≥4ac，得：（2a+b）2≥4a，由于求t的最大值，只需考虑a，b＞0（不然则t＝min{a，b}≤0）此时由（2a+b）2≥4a，得：1≥4t，故t≤，∴max{min{a，b，c}}＝．故答案为：．【点睛】本题考查三个数的最大值的最小值的求法，考查二次函数的性质等基础知识，综合程度较高，考查化归与转化思想，考查运算求解能力，属于难题．14．（2019•浙江模拟）已知实数f（x）＝，若关于x的方程f2（x）+f（x）+t＝0有三个不同的实根，则t 的取值范围为（﹣∞，﹣2]．【解析】解：原问题等价于f2（x）+f（x）＝﹣t有三个不同的实根，即y＝﹣t与y＝f2（x）+f（x）有三个不同的交点，当x≥0时，y＝f2（x）+f（x）＝e2x+e x为增函数，在x＝0处取得最小值为2，与y＝﹣t只有一个交点．当x＜0时，y＝f2（x）+f（x）＝lg2（﹣x）+lg（﹣x），根据复合函数的单调性，其在（﹣∞，0）上先减后增．所以，要有三个不同交点，则需﹣t≥2，解得t≤﹣2．【点睛】本题考查了函数与方程的综合运用，属难题．15．（2019秋•临沂期中）设△ABC的内角A，B，C的对边分别为a，b，c，已知a，b，c依次成等比数列，且cos（A﹣C）﹣cos B＝，则sin C＝．【解析】解：∵cos（A﹣C）﹣cos B＝，∴cos（A﹣C）+cos（A+C）＝，得cos A cos C＝．∵a，b，c成等比数列，∴b2＝ac，∴sin2B＝sin A sin C，则cos A cos C﹣sin A sin C＝﹣sin2B，∴﹣cos B＝，即，解得cos B＝，∴B＝，则sin B＝．∴，又cos A cos C＝，∴cos A cos C+sin A sin C＝1，即cos（A﹣C）＝1，∵﹣＜A﹣C＜，∴A﹣C＝0，则A＝C＝，∴sin C＝．故答案为：．【点睛】本题考查三角形的解法，考查两角和与差的三角函数的应用，考查计算能力，是基础题．16．（2019秋•嘉善县校级月考）已知平面向量，，且||＝2，||＝1．若平面向量满足||＝||，则||的最大值．【解析】解：由||＝2，||＝1．得2+2+2•＝4，2+2﹣2•＝1，两式相加得2（2+2）＝5，又||＝||，所以||﹣||≤||＝||，即||≤||+||，当且仅当与反向时等号成立，而5＝2（2+2）≥（||+||）2，当且仅当||＝||时等号成立，||2≤（||+||）2≤5，当且仅当与反向，||＝||时等号成立，则||的最大值为．故答案为：．【点睛】本题考查了平面向量的模，基本不等式、三角不等式的应用，是中档题．三．解答题（共6题，第17题10分，第18~22题每题12分，共70分）17．（2019秋•徐州期中）已知集合A＝{x|3≤3x≤27}，B＝{x|1＜log2x＜2}．（1）分别求A∩B，（∁R B）∪A；（2）已知集合C＝{x|2a＜x＜a+2}，若C⊆A，求实数a的取值范围．【解析】解：（1）因为A＝{x|3≤3x≤27}＝{x|1≤x≤3}，B＝{x|1＜log2x＜2}＝{x|2＜x＜4}，所以A∩B＝{x|2＜x≤3}，从而（∁R B）∪A＝{x|x≤3或x≥4}．（2）当2a≥a+2，即a≥2时C＝∅，此时C⊆A，符合条件；当2a＜a+2，即a＜2时，C≠∅，要使C⊆A，只需即．故要使C⊆A，实数a的取值范围是{a|a≥2或}．【点睛】本题考查交集、补集、并集的求法，考查交集、补集、并集定义等基础知识，考查运算求解能力，是基础题．18．（2019秋•碑林区期中）已知函数．（1）求函数的定义域；（2）判断函数f（x）的奇偶性，并进行证明；（3）若f（x）＜m2﹣2am+1，对所有x∈[﹣1，1]，a∈[﹣1，1]恒成立，求实数m的取值范围．【解析】解：（1）∵f（x）＝，∴＞0，∴﹣2＜x＜2；∴定义域为（﹣2，2）．（2）∵定义域关于原点对称，且f（﹣x）＝＝＝﹣f（x）；故函数f（x）为奇函数．（3）设u＝，y＝；f（x）是由两个函数复合而成的，由于u＝＝﹣1在（﹣2，2）上是减函数；y＝；在（0，+∞）上也是减函数；由复合函数单调性知，f（x）在（﹣2，2）上是增函数．∴f（x）在[﹣1，1]上是增函数．所以f（x）在[﹣1，1]上的最大值为f（1）＝1，所以要使f（x）＜m2﹣2am+1对所有x∈[﹣1，1]，a∈[﹣1，1]恒成立，只要m2﹣2am+1＞1，即m2﹣2am＞0恒成立．令g（a）＝m2﹣2am＝﹣2ma+m2，则g（a）min＞0，即，解得m＞2或m＜﹣2．故实数m的取值范围是{m|m＞2或m＜﹣2}．【点睛】本题考查了对数函数及其应用，函数的奇偶性，函数的单调性，函数恒成立问题，属于中档题．19．（2019•西湖区校级模拟）已知f（x）是定义在R上的奇函数，且x＜0时，f（x）＝（）（x+1）．（1）求f（0），f（1）；（2）求函数f（x）的解析式；（3）若f（a﹣1）＜1，求实数a的取值范围．【解析】解：（1）因为f（x）为R上的奇函数，所以f（0）＝0，f（1）＝﹣f（﹣1）＝﹣＝﹣1；（2）设x＞0，则﹣x＜0，所以f（x）＝﹣f（﹣x）＝﹣＝﹣2x﹣1，又由（1）知f（0）＝0，所以f（x）＝；（3）①当a﹣1＞0即a＞1时，f（a﹣1）＜1⇔﹣2（a﹣1）﹣1＜1，解得a＞1；②当a﹣1＝0即a＝1时，f（a﹣1）＜1⇔0＜1，成立；③当a﹣1＜0即a＜1时，f（a﹣1）＜1⇔＜1，解得0＜a＜1；综上实数a的取值范围为（0，+∞）．【点睛】本题考查了函数的奇偶性，考查了奇函数对称区间上的解析式的求法，考查了不等式的解法．考查推理运算能力．属于中档题．20．（2019秋•无锡期中）为了丰富学生活动，在体育课上，体育教师设计了一个游戏，让甲、乙、丙三人各抓住橡皮带的一端，甲站在直角△ABC斜边AC的中点F处，乙站在B处，丙站在C处游戏开始，甲不动，乙、丙分别以v（m/s）和2v（m/s）的速度同时出发，匀速跑向终点A和B．运动过程中绷紧的橡皮带围成一个如图所示的△DEF．（规定：只要有一人跑到终点游戏就结束，且0＜v≤3（m/s））．已知AB长为40m，BC长为80m，记经过t（s）后△DEF的面积为S（m2）．（1）求S关于t的函数表达式，并求出t的取值范围；（2）当游戏进行到10s时，体育教师宣布停止，求此时S（m2）的最小值．【解析】解：（1）AC＝＝40，sin A＝＝，sin C＝，S△ABC＝＝1600，t秒后，AD＝40﹣vt，BD＝vt，BE＝80﹣2vt，CE＝2vt，AF＝CF＝20，故S△BDE＝•BD•BE＝﹣v2t2+40vt，S△ADF＝AD•AF•sin A＝800﹣20vt，S△CEF＝CF＝20vt，∴S△DEF＝S△ABC﹣S△BDE﹣S△ADF﹣S△CEF＝1600﹣（﹣v2t2+40vt）﹣（800﹣20vt）﹣20vt＝v2t2﹣40vt+800，即S（t）＝v2t2﹣40vt+800，（0＜t≤）．（2）设BD＝vt＝x，则S＝x2﹣40x+800＝（x﹣20）2+400，∵0＜v≤3，t＝10，故0＜x≤30，∴当x＝20时，S取得最小值400．故S的最小值为400．【点睛】本题考查了函数解析式的求解，函数最值的计算，属于中档题．21．（2019秋•香坊区校级月考）已知函数＝（，，（1）求函数f（x）在[0，π]上的单调递增区间和最小值．（2）在△ABC中，a，b，c分别是角A，B，C的对边，且f（B）＝2，，求cos A的值．【解析】解：（1）根据题意得；f（x）＝＝＝＝＝＝，令，∵x∈[0，π]，函数f（x）在[0，π]上的单调递增区间为[0，]；最小值为﹣2．（2）∵，∵∵∴＝＝∴，∴＝＝，∴．【点睛】第（1）向量的数量积运算要正确，否则后续全错．第（2）问关键要正弦定理把边的关系转化为角的关系，难点在凑角的技巧上．22．（2019春•雨花区校级期中）已知向量＝（，1），＝（cos，），记f（x）＝．（1）求函数f（x）的最小正周期和单调递增区间；（2）将函数y＝f（x）的图象向右平移个单位得到y＝g（x）的图象，讨论函数y＝g（x）﹣k在的零点个数．【解析】解：（1）∵向量＝（，1），＝（cos，），记f（x）＝．∴f（x）＝•cos+＝sin+cos+＝sin（+）+，∴最小正周期T＝＝4π，2kπ﹣≤+≤2kπ+，则4kπ﹣≤x≤4kπ+，k∈Z．故函数f（x）的单调递增区间是[4kπ﹣，4kπ+]，k∈Z；（2）∵将函数y＝f（x）＝sin（+）+的图象向右平移个单位得到函数解析式为：y＝g（x）＝sin[（x﹣+）]+＝sin（﹣）+，∴则y＝g（x）﹣k＝sin（x﹣）+﹣k，∵x∈[0，]，可得：﹣≤x﹣≤π，∴﹣≤sin（x﹣）≤1，∴0≤sin（x﹣）+≤，∴若函数y＝g（x）﹣k在[0，]上有零点，则函数y＝g（x）的图象与直线y＝k在[0，]上有交点个数即为零点个数，∴当≤k＜时，函数y＝g（x）﹣k在的零点个数是2；当0≤k＜或k＝时，函数y＝g（x）﹣k在的零点个数是1．【点睛】本题是中档题，考查向量的数量积的应用，三角函数的化简求值，函数的单调增区间的求法，函数零点的判断方法，考查计算能力．。

高一数学必修一、必修四期末试卷高一数学期末试卷（必修一、必修四）一、选择题（本大题共10小题，每小题4分，共40分）1.函数y=2x+1+3-4x的定义域为（）A.(-∞,)B.[-1,2]C.(-∞,]∪[2,∞)D.(-∞,-1)∪(2,∞)2.函数y=-2sin(x+π/4)的周期，振幅，初相分别是（）A.2π，2，-π/4B.4π，-2，-π/4C.4π，2，-π/4D.2π，2，-π/43.设f(x)=3+3x-8,用二分法求方程3+3x-8=0在x∈(1,2)内近似解的过程中得f(1)0,f(1.25)<0，则方程的根落在区间（）A.（1,1.25）B.（1.25,1.5）C.（1.5,2）D.不能确定4.函数f(x)=sinx·cosx是(。

)B.周期为π的奇函数5.已知函数f(x)=4+ax-1的图象恒过定点p，则点p的坐标是（）B.（1.4）6.给出命题(。

)(1)零向量的长度为零，方向是任意的.(3)向量AB与向量BA相等.(4)若非零向量AB与CD是共线向量，则A，B，C，D四点共线.以上命题中，正确命题序号是D.（1）和（4）7.函数y=(2a-3a+2)a是指数函数，则a的取值范围是（）A.a>0,a≠18.若α是第一象限角，则sinα+cosα的值与1的大小关系是(。

)A.sinα+cosα>19.在△ABC中，若sinC=2cosAsinB，则此三角形必是()D.等腰直角三角形10.如图，在△ABC中，AD、BE、CF分别是BC、CA、AB上的中线，它们交于点G，则下列各等式中不正确的是()C.DG=AG二、填空题（本大题共4小题，每小题4分，共16分）1.52.π/43.1.25,1.54.π的奇函数5.（1,4）6.（1）和（4）7.a>0,a≠18.sinα+cosα>19.等腰直角三角形10.无法填空4sinα-2cosα=5cosα+3sinα的解为______。

数 学（必修1,4 ）试 题一、选择题：（每题5分，满分60分）1.已知α是第四象限角，且cos 02α>，则2α所在的象限是（ ）A. 第一象限角B. 第二象限角C. 第三象限角 D . 第四象限角3. 下列命题正确的是（ ）A 若→a ·→b =→a ·→c ，则→b =→cB 若||||b -=+，则→a ·→b =0C 若→a //→b ，→b //→c ，则→a //→cD 若→a 与→b 是单位向量，则→a ·→b =14．函数y= | lg （x-1）| 的图象是 （ ）5. 已知a 、b 是非零向量且满足(2)-⊥a b a ，(2)-⊥b a b ，则a 与b 的夹角是A ．6πB ．3πC ．32πD ．65π6.下列函数为偶函数，且在(),0-∞上单调递增的函数是（ ）A. ()23f x x =B. ()3f x x -=C. ()12xf x ⎛⎫= ⎪⎝⎭ D. ()ln f x x =8.已知3.0log a 2=，3.02b =，2.03.0c =，a,b,c 的大小关系是 （ ）A 、a c b >>B 、c a b >>C 、c b a >>D 、a b c >>二、填空题：（每题5分，满分25分）13.在边长为1的正三角形ABC 中，设3,2==，则=∙BE AD15．给出下列命题：①()sin 100-<； ②函数y ＝sin(2x ＋5π4)的图像关于点,08π⎛⎫- ⎪⎝⎭对称； ③将函数y ＝cos(2x －π3)的图像向左平移π3个单位，可得到函数y ＝cos2x 的图像； ④函数tan 24y x π⎛⎫=+ ⎪⎝⎭的最小正周期是4π.其中正确的命题的序号是 .三、解答题：（本题满分76分，要求写出必要的步骤和过程）16. (12分)化简与计算(1)14731622329log log log log log log ⎛⎫ ⎪⎝⎭-++⨯ （2）已知2tan =α，求)sin()tan()23sin()2cos()sin(αππαπααπαπ----+---的值17.61)2()32(,34=+∙-==b a b a（1）求与的夹角θ；（2b ；（3）若,,b BC a AB ==求三角形ABC 的面积.18.已知21tan ,2)4tan(==+∏βα (1)求)2tan(α的值.（2求)cos(sin sin 2cos sin 2)sin(βαβαβαβα++-+的值.20.（本小题满分13分）已知函数2()2sin ()24f x x x π=+，[,]42x ππ∈. （1）求函数()f x 的单调区间和最值；（2）若不等式()2f x m -<在[,]42x ππ∈上恒成立，求实数m 的取值范围.。

高一数学第一学期期末考试题一、 选择题1、已知集合{},5<∈=x Z x M 则下列式子正确的是（ ）A ．M ∈5.2B ．M ⊆0C ．M ⊆}0{D ．M ∈}0{2、下列四个图象中，是函数图象的是 （ ）A ．（1） B.（1）（3）（4） C.（1）（2）（3） D.（3）（4）3、已知角α的终边过点P （-4，3），则ααcos sin 2+的值为（ ）A ．54- B ．53 C ．52D ．24、设)2,0(πα∈，若53sin =α，则)4cos(2πα+等于（ ）A ．57B ．51C ．57- D ．51-5、若θθcos sin ⋅>0,则θ在（ ）A ．第一、二象限B ．第一、三象限C ．第一、四象限D ．第二、四象限6、函数log (2)1a y x =++的图象过定点（ ）A.（1，2）B.（2，1）C.（-2，1）D.（-1，1）7、已知2log 3=a ，那么6log 28log 33-用a 表示为（ ）A.2-aB.25-aC.2)(3a a a +-D.132--a a8．已知)(x f 是偶函数，且0>x 时，ax x x f +=2)(，若2)1(=-f ，则)2(f 的值是（）A ．1-B ． 1C ． 3D ． 69、若a 、b 是任意实数，且a >b ,则（ ）A. a 2>b 2B. ab <1 C. ()lg a b ->0 D.12a ⎛⎫ ⎪⎝⎭<12b⎛⎫⎪⎝⎭10、已知54cos ),0,2(=-∈x x π，则=x 2tan （ ）A ．247B ．247- C ．724 D ．724-（1） （2） （3） （4）11、要得到)42cos(π-=x y 的图像只需要将函数x y 2cos =的图像（ ） A ．向左平移8π个单位 B ．向右平移8π个单位 C ．向左平移4π个单位 D ．向右平移4π个单位 12、函数)20,0,)(sin(πϕωϕω<≤>∈+=R x x y 的部分图象如图，则（ ）A ．4,2πϕπω==B ．6,3πϕπω==C ．4,4πϕπω==D ．45,4πϕπω== 二、填空题 13、函数()()1log 143++--=x x x x f 的定义域是 。