7.1生活中的不等式

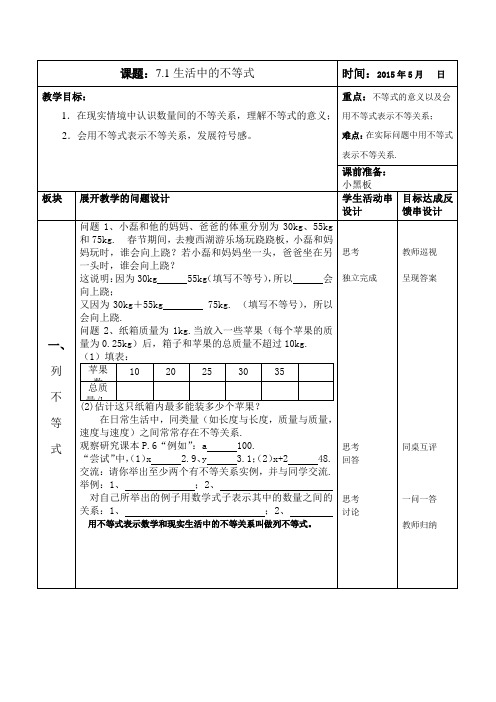
7.1生活中的不等式目标要求：1．在现实情境中认识数量间的不等关系，理解不等式的意义；2．会用不等式表示不等关系.过程性目标：1．引导学生分析具体事例，从对具体事例的分析中得到不等量关系；2．通过分析、抽象得到不等式的概念情感态度目标：1．在对实际问题的数量关系进行比较分析、作出推断的过程中，提高学生参与数学活动，乐于接触社会环境中数学信息的兴趣；2．为学生创设学数学、用数学的情境，让学生体验用数学知识解决实际问题的方法．重点和难点重点：不等式的意义以及会用不等式表示不等关系；难点：在实际问题中用不等式表示不等关系.一、情境创设（体会生活中的不等关系）：1、小磊和他的妈妈、爸爸的体重分别为30kg、55kg和75kg.春节期间，去瘦西湖游乐场玩跷跷板，小磊和妈妈玩时，谁会向上跷？若小磊和妈妈坐一头，爸爸坐在另一头时，谁会向上跷？这说明：因为30kg55kg（填写不等号），所以会向上跷；又因为30kg＋55kg75kg. （填写不等号），所以会向上跷.2、一只纸箱质量为1kg.当放入一些苹果（每个苹果的质量为0.25kg）后，箱子和苹果的总质量不超过10kg.（1）填表：苹果数10 20 25 30 35总质量/kg(2)估计这只纸箱内最多能装多少个苹果？二、学习新知：（一）认识不等号：> 大于；< 小于；≠ 不等于；≤ 小于或等于（不大于）；≥ 大于或等于（不小于）（二）认识不等式：用不等号表示不等关系的式子叫做不等式.1. 下列式子中，哪些是不等式？哪些不是?(1) –2 < 0 ；(2) 2a > 3-a ；(3)3x+5；(4) ≥0；(5) s = vt；(6) ；(7) 3 > 5；(8) 5x≤4x-1.2. 用“<，>，≤，≥”填空：(1) －0.3___0；(2) 5____ ；(3) 4 ；(4)－；(5) x 2 0 (6)(7) - x 2 0 （8）x 2 -1 （9）- x 2 23. 用不等式表示：（1）x小于-6 （2）x+1大于0 （3）x 大于或等于5（4）x 小于或等于-8 （5）x 不大于6 （6）x 不小于-2（7）x 是正数（8）x 是负数（9）x 是非负数(10) x与5的和大于2 （11）x与a的差小于2 （12）x与y的差是负数（13）x 与y的和是非负数（14）x的2倍与5的和是正数（15）x 与3的差是负数（16）x 的3倍与y的2倍的和是非负数（三）用不等式表示下列数量之间的关系（将文字语言转化为不等式）：1. 某种客车坐有x人，它的最大载客量为40人．2. 小明每天跑步x 分钟，学校规定每位学生每天跑步时间不少于30分钟．3. 某校男子跳高记录是1.75 米，小强在今年的运动会上打破了校纪录．教后反思：在现实生活中认识数量之间的不等关系，理解了不等式的意义，学生学会了用不等式表示不等关系，这节课内容学生接受起来还是属于较简单的。

不等式（组）在实际生活中的应用不等式（组）在实际生活中的应用不等式：概念定义：一般地，用符号“<”（或“≤”），“>”（或“≥”）,“≠”连接的式子叫做不等式。

用不等号连接的，含有一个未知数，并且未知数的次数都是1，系数不为0，左右两边为整式的式子叫做一元一次不等式。

不等式性质（1）不等式的两边都加上（或减去）同一个数(或式子)（0除外），不等号的方向不变。

（2）不等式的两边都乘以（或除以）同一个正数，不等号的方向不变。

（3）不等式的两边都乘以（或除以）同一个负数，不等号的方向改变。

用字母表示不等式的性质1.性质1：如果a>b,那么（a±c>b±c)。

2.性质2：如果a>b，c>0，那么ac>bc(或a/c>b/c)。

3.性质3：如果a>b，c<0，那么ac<="" c不等式解集一个有未知数的不等式的所有解，组成这个不等式的解集。

求不等式解集的过程叫做解不等式。

不等式的解集可以在数轴上直观地表示出来，形象地说明不等式有无限多个解。

不等式组：概念定义：一般地，关于同一个未知数的几个一元一次不等式合在一起，就组成一个一元一次不等式组。

不等式组的解集一元一次不等式组中各个不等式的解集的公共部分，叫做这个一元一次不等式组的解集。

求不等式组解集的过程，叫做解不等式组。

常见解法取解集的方法可归纳为：两大取大，两小取小，大小小大取中间，大大小小取空集。

特殊不等式组解（1）关于x不等式（组）：{x≥a} { x≤a}的解集为：x=a。

（2）关于x不等式（组）：{xa} 的解集是空集。

在数轴上表示解集时应注意：大于向右画，小于向左画；有等号的画实心圆点，无等号的画空心圆圈。

一元一次不等式组解应用题的一般步骤1、审：审清题意，弄懂已知什么，求什么，以及各个数量之间的关系。

2、设：只能设一个未知数，一般是与所求问题有直接关系的量。

现实生活中的不等式现实生活的实际问题中有很多的不等关系，同窗们多留意，观看身旁的事物，会发觉数学就在咱们的身旁。

一、天气预报的不等关系例1、据丽水气象台“天气预报”报导，今天的最低气温是17℃，最高气温是25℃，那么今天气温t （℃）的范围是（ ）（A ）t ＜17 （B ）t ＞25 （C ）t=21 （D ）17≤t≤25解：最低气温是17℃，指气温t≥17，最高气温是25℃，指t≤25，因此，气温t （℃）的范围是17≤t≤25，应选（D ）。

二、跷跷板中的不等关系例2、图1是甲、乙、丙三人玩跷跷板的示用意（支点在中点处），那么甲的体重的取值范围在数轴上表示正确的选项是（ ）（ A ） （B ）（C ） （D ）解：图1的左图中，甲沉下去，可知甲的体重大于40kg；图1的右图中，丙沉下去，甲的体重小于50kg ，设甲的体重为xkg ，那么40＜x ＜50，在数轴上表示，应选（C ）。

例2、2006浙江丽水）依照神舟六号船环境操纵与生命保障系统的设计指标，要求神舟六号飞船返回舱的温度在21°C±4°C 之间，那么该返回舱中温度t(°C)的范围是（ ）（A ）17≤t≤25 （B ）25≤t≤17 （C ）t≥17（D ）t≤25解：温度在21°C±4°C之间，确实是指在（21°C－4°C）和（21°C＋4°C）之间，即在17°C 与25°C 之间，应选（A ）。

三、天平中的不等关系例3、依照以下图所示，对a 、b 、c 三中物体的重量判定正确的选项是 ( ）甲乙40kg 丙50kg 甲 图1 4050 40 5040 50 40 50（A ）a ＜c （B ）a ＜b （C ）a ＞c （D ）b ＜c 解：由左图可知，2a ＝3b ，由右图可知，2b ＝3c ，即：⎩⎨⎧==cb b a 9664，得：4a ＝9c ，因此a ＞c ，应选（C ）。

生活中的不等式教学设计一．教材分析不等式是解决实际问题的一种数学模型，它不仅是初中阶段学习的重点内容，而且也是后面学习函数等知识的基础.它是在学习了一元一次方程、二元一次方程组之后的后续内容，贯穿于数学学习的始终,起着横贯上下的作用.本节是本章的第一课时，主要学习一个概念,不等式的概念。

二．学情分析学生在小学对不等量关系、数量大小的比较等知识已经有所了解,但对含有未知数的不等式还是第一次接触，本节就是对“不等”这一概念进一步明确，使它成为一种有效的数学模型.学生在列不等式时，对数量关系中的“不大于”、“不小于”、“负数”、“非负数”等数学术语的含义不能准确理解，在把用文字语言表述的不等关系转化为用符号表示的不等式时有一定困难.由于不等式定义概念是学习不等式的重要基础，因此这是是本节课教学中的重点；而如何根据具体的情景列出不等式，这将是我们本节课研究的难点.三．教学目标依据《教学大纲》及对教材的分析，结合学生已有的知识储备及年龄特征，本节课的教学目标是：（1）在现实情境中认识数量间的不等关系，理解不等式的意义；（2）会用不等式表示不等关系。

（3）经历由具体问题建立不等式的过程，初步体会不等式是刻画现实世界的一种数学模型四．教学重点、难点教学重点：了解不等式的意义，会用不等式表示不等关系。

教学难点：在实际问题中用不等式表示不等关系。

五．教学策略本着“以学生的发展为本”的教育理念，同时也为了使学生积极主动的参与课堂活动，充分发挥学生的主观能动性。

本节课主要采用了引导探究，小组活动，合作交流的教学方式，通过设置数学活动问题串，引导学生思考，增加学生参与课堂的机会及体验获取知识的过程，本节课还采用多媒体的动画效果进行直观教学，有效地调动学生学习数学的积极性。

六．教学准备每人准备一盒牛奶七．教学过程设计7.1 创设情境引入新课播放视频《小羊肖恩减肥》，提出以下问题：问题（1）动画片中的小羊们机智而又团结，请问小羊们机智在何处?（2）当天平平衡时，两边物体质量相等，那我们是如何刻画相等关系的呢？（3）当拿掉一些砖头后，“天平”为什么会倾斜？意图：通过动画片拉近与学生的距离，通过动画片中的一个片段，天平的平衡到不平衡，自然从相等关系过渡到不等关系。

八年级下册数学课本目录苏科第七章一元一次不等式7.1生活中的不等式7.2不等式的解集7.3不等式的性质7.4解一元一次不等式7.5用一元一次不等式解决问题7.6一元一次不等式组7.7一元一次不等式与一元一次方程、一次函数第八章分式8.1分式8.2分式的基本性质8.3分式的加减8.4分式的乘除8.5分式方程第九章反比例函数9.1反比例函数9.2反比例函数的图象与性质9.3反比例函数的应用第十章图形的相似10.1图上距离与实际距离10.2黄金分割10.3相似图形10.4探索三角形相似的条件 10.5相似三角形的性质 10.6图形的位似10.7相似三角形的应用第十一章图形与证明一 11.1你的判断对吗11.2说理11.3证明11.4 互逆命题第十二章认识概率 12.1等可能性12.2等可能条件下的概率一 12.3等可能条件下的概率二7.1用不等号表示不等关系的式子叫做不等式7.2不等式的性质：1不等式的两边都加上或减去同一个整式，不等号的方向不变。

2不等式的两边都乘或除以不为0正数，不等号的方向不变;不等式的两边都乘或除以负数，不等号的方向改变7.4解一元一次不等式的步骤与解一元一次方程类似。

但是，在不等式两边都乘或除以同一个不等于0的数时，必须根据这个数是正数，还是负数，正确地运用不等式的性质 2特别要注意在不等式两边都乘或除以同一个负数时，要改变不等号的方向7.5用一元一次不等式解决问题7.6由几个含有同一个未知数的一次不等式组成的不等式组叫做一元一次不等式组。

不等式组中所有不等式的解集的公共部分叫做这个不等式组的解集，求不等式组解集的过程叫解不等式组。

7.7一元一次不等式与一元一次方程、一次函数当一次函数中的一个变量的值确定时，可以用一元一次方程确定另一个变量的值;当已知一次函数中的一个变量范围时，可以用一元一次不等式组确定另一个变量取值的范围。

感谢您的阅读，祝您生活愉快。