图形的初步认识专题复习
- 格式:doc
- 大小:848.50 KB
- 文档页数:12


《图形认识初步》1、几何图形:我们把实物中抽象出来的各种图形叫做几何图形。
几何图形分为平面图形和立体图形。
(1)平面图形:图形所表示的各个部分都在同一平面内的图形,如直线、三角形等。
(2)立体图形:图形所表示的各个部分不在同一平面内的图形,如圆柱体。
2、常见的立体图形(1)柱体:A 棱柱---有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边互相平行,由这些面围成的几何体叫做棱柱。
B 圆柱---以矩形的一边所在直线为旋转轴,其余各边围绕它旋转一周二形成的曲面所围成的集合体叫做圆柱。
(2)椎体:A 棱锥—有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
B 圆锥—以直角三角形的一条直角边所在的直线为旋转轴,其余各边旋转一周而形成的曲面围成的几何体叫做圆锥。
(3)球体:半圆以它的直径为旋转轴,旋转一周而形成的曲面所围成的几何体叫做球体。
(4)多面体:围成棱柱和棱锥的面都是平的面,想这样的立体图形叫做多面体。
3、 常见的平面图形(1)多边形:由线段围成的封闭图形叫做多边形。
多边形中三角形是最基本的图形。
(2)圆:一条线段绕它的端点旋转一周而形成的图形。
(3)扇形:由一条弧和经过这条弧的端点的两条半径围成的图形叫做扇形。
4、 从不同方向观察几何体从正面、上面、左面三个不同方向看一个物体,然后描出三张所看到的图(分别叫做正视图、俯视图、侧视图),这样就可以把立体图形转化为平面图形。
例题:1、如图是一些小正方体所搭几何体的俯视图,小正方形中的数字表示该位置的小正方体的个数,请画出这个几何体的主视图和左视图:主视图 左视图例题:2、下列左图表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则该几何体的主视图为 ( )5、 立体图形的展开图有些立体图形是有一些平面图形围成的,把它们的表面适当剪开后在平面上展开得到的平面图形称为立体图形的展开图。

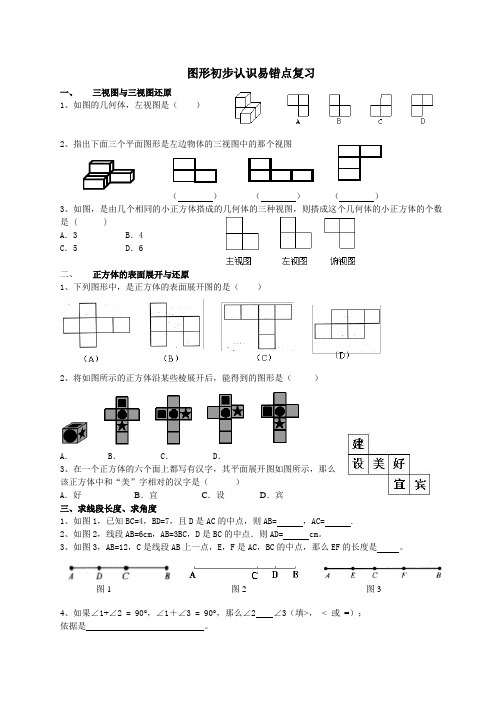
图形初步认识易错点复习一、三视图与三视图还原1、如图的几何体,左视图是()2、指出下面三个平面图形是左边物体的三视图中的那个视图()()()3、如图,是由几个相同的小正方体搭成的几何体的三种视图,则搭成这个几何体的小正方体的个数是 ( )A.3 B.4C.5 D.6二、正方体的表面展开与还原1、下列图形中,是正方体的表面展开图的是()2、将如图所示的正方体沿某些棱展开后,能得到的图形是()A. B. C. D.3、在一个正方体的六个面上都写有汉字,其平面展开图如图所示,那么该正方体中和“美”字相对的汉字是()A.好B.宜C.设D.宾三、求线段长度、求角度1、如图1,已知BC=4,BD=7,且D是AC的中点,则AB= ,AC= .2、如图2,线段AB=6cm,AB=3BC,D是BC的中点.则AD= cm。
3、如图3,AB=12,C是线段AB上一点,E,F是AC,BC的中点,那么EF的长度是。
4、如果∠1+∠2 = 90°,∠1+∠3 = 90°,那么∠2 ∠3(填>,< 或=);依据是。
图1 图2 图35、解答题(1)点C在线段AB上,AC=10cm,CB=8cm,点M、N分别是AC、BC的中点,求线段MN的长。
(2)如图,AB=12cm,点C是线段AB的中点,点D是线段CB的中点,求线段AD的长。
(3)如图,点C是线段AB的中点,点D是线段BC的中点,CD=5cm,求线段AD的长度。
(4)如图,已知点O是直线AB上一点,OD,OE分别是∠AOC,∠COB的平分线,∠AOD=50°。
(1)求∠BOE的度数;(2)试判断OD与OE是否垂直,并说明理由。
(5)如图,已知A、C、B三点共线,CE,CF分别是∠BCD,∠ACD的平分线,求∠ECF的度数。

初中数学中考复习考点知识与题型专题讲解专题15 图形的基本认识【知识要点】考点知识一立体图形⏹立体图形概念:有些几何图形的各部分不都在同一个平面内。
常见的立体图形:棱柱、棱锥、圆柱、圆锥、球等。
⏹平面图形概念:有些几何图形的各部分不都在同一个平面内。
常见的平面图形:线段、角、三角形、长方形、圆等【立体图形和平面的区别】1、所含平面数量不同。
平面图形是存在于一个平面上的图形。
立体图形是由一个或者多个平面形成的图形,各部分不在同一平面内,且不同的立体图形所含的平面数量不一定相同。
2、性质不同。
根据“点动成线,线动成面,面动成体”的原理可知,平面图形是由不同的点组成的,而立体图形是由不同的平面图形构成的。
由构成原理可知平面图形是构成立体图形的基础。
3、观察角度不同。
平面图形只能从一个角度观察,而立体图形可从不同的角度观察,如左视图,正视图、俯视图等,且观察结果不同。
4、具有属性不同。
平面图形只有长宽属性,没有高度;而立体图形具有长宽高的属性。
立方体图形平面展开图三视图及展开图三视图:从正面,左面,上面观察立体图形,并画出观察界面。
考察点:(1)会判断简单物体(直棱柱、圆柱、圆锥、球)的三视图。
(2)能根据三视图描述基本几何体或实物原型。
展开图:正方体展开图(难点)。
正方体展开图口诀(共计11种):“一四一”“一三二”,“一”在同层可任意,“三个二”成阶梯,“二个三”“日”相连,异层必有“日”,“凹”“田”不能有,掌握此规律,运用定自如。
⏹点、线、面、体几何图形的组成:点:线和线相交的地方是点,它是几何图形最基本的图形。
线:面和面相交的地方是线,分为直线和曲线。
面:包围着体的是面,分为平面和曲面。
体:几何体也简称体。
组成几何图形元素的关系:点动成线,线动成面,面动成体。
考点知识二直线、射线、线段⏹直线、射线、线段的区别与联系:【射线的表示方法】表示射线时端点一定在左边,而且不能度量。
经过若干点画直线数量:1.经过两点有一条直线,并且只有一条直线(直线公理)。

中考复习——七年级上第六章《图形的认识初步》专题总结一、知识网络1、通常画一个立体图形要分别从正面看、从左面看、从上面看.如从不同方向看图2就可得到三个图形.2、在研究直线、线段、射线的有关概念时,容易出现延长直线或延长射线之类的错误,在用两个大写字母表示射线时,忽视第一个字母表示的是这条射线的顶点.3、直线有这样一个重要性质:经过两点有一条直线,并且只有一条直线。
即两点确定一条直线。
线段有这样一条重要性质:两点的所有连线中,线段最短。
简单说成:两点之间,线段最短。
4、注意线段的中点是指把线段分成相等的两条线段的点;而连结两点间的线段的长度,叫做这两点的距离.这里应特别注意线段与距离的区别是,即距离是线段的长度,是一个量;线段则是一种图形,它们之间是不能等同的.5、在复习角的概念时,应注意理解两种方式来描述,即一种是有公共端点的两条射线组成的图形,叫做角;另一种是用旋转的观点来定义,即一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角。
角的两种定义都告诉我们这样一些事实:(1)角有两个特征:一是角有两条射线,二是角的两条射线必须有公共端点,两者缺一不可。
(2)由于射线是图2从正面看 从左面看 从上面看向一方无限延伸的,所以角的两边无所谓长短,即角的大小与它边的长短无关;(3)当角的大小一旦确定,它的大小就不因图形的位置、图形的放大或缩小而改变。
如一个37°的角放在放大或缩小若干倍的放大镜下它仍然是37°不能误认为角的大小也放大或缩小若干倍。
另外对角的表示方法中,当用三个大写字母来表示时,顶点的字母必须写在中间,在角的两边上各取一点,将表示这两个点的字母分别写在顶点字母的两旁,两旁的字母不分前后。
6、直线、射线、线段 基本概念直线公理:经过两点有且只有____条直线. 线段公理:两点之间,_________最短.[点拨] 两个点之间连线有很多条,但只有线段最短,把这条线段的长度,就叫做这两点之间的________.[总结] (1)当一条直线上有n 个点时,在这条直线上存在_____________条线段.下列说法中正确的是( )A 、延长射线OPB 、延长直线CDC 、延长线段CD D 、反向延长直线CD互余、互补(1)若∠1+∠2=90°,则∠1与∠2互为余角。
图形的初步认识复习3.图形变换思想。
在研究⾓的概念时,要充分体会对射线旋转的认识。
在处理图形时应注意转化思想的应⽤,如⽴体图形与平⾯图形的互相转化。
4.化归思想。
在进⾏直线、线段、⾓以及相关图形的计数时,总要划归到公式n(n-1)/2的具体运⽤上来。
⼀、本章的知识结构图⼆、知识回顾本章的主要内容是图形的初步认识,从⽣活周围熟悉的物体⼊⼿,对物体的形状的认识从感性逐步上升到抽象的⼏何图形。
通过从不同⽅向看⽴体图形和展开⽴体图形,初步认识⽴体图形与平⾯图形的联系。
在此基础上,认识⼀些简单的平⾯图形——直线、射线、线段和⾓。
⼀、⽴体图形与平⾯图形例1 (1)如图1所⽰,上⾯是⼀些具体的物体,下⾯是⼀些⽴体图形,试找出与下⾯⽴体图形相类似的物体。
(2)如图2所⽰,写出图中各⽴体图形的名称。
图1图2解:(1)①与d类似,②与c类似,③与a类似,④与b类似。
(2)①圆柱,②五棱柱,③四棱锥,④长⽅体,⑤五棱锥。
例2 如图3所⽰,讲台上放着⼀本书,书上放着⼀个粉笔盒,指出右边三个平⾯图形分别是左边⽴体图形的哪个视图。
图3解:(1)左视图,(2)俯视图,(3)正视图练习1.下图是⼀个由⼩⽴⽅体搭成的⼏何体由上⽽看得到的视图,⼩正⽅形中的数字表⽰该位置⼩⽴⽅块的个数,则从正⾯看它的视图为()2.如图,把左边的图形折叠起来,它会变成右边的正⽅体是右边的()3.如图,下⾯三个正⽅体的六个⾯按相同规律涂有红、黄、蓝、⽩、⿊、绿六种颜⾊,那么涂黄⾊、⽩⾊、红⾊的对⾯分别是()A.蓝、绿、⿊ B.绿、蓝、⿊ C.绿、⿊、蓝 D.蓝、⿊、绿4.若如下平⾯展开图折叠成正⽅体后,相对⾯上的两个数之和为5,求x+y+z的值。
5.⼀个物体从不同⽅向看的视图如下,画出该物体的⽴体图形。
⼆、直线、射线、线段(⼀).直线、射线、线段的区别与联系:从图形上看,直线、射线可以看做是线段向两边或⼀边⽆限延伸得到的,或者也可以看做射线、线段是直线的⼀部分;线段有两个端点,射线有⼀个端点,直线没有端点;线段可以度量,直线、射线不能度量。
个人收集整理资料,仅供交流学习,勿作商业用途7-4 第四章、图形认识初步专题复习姓名:第一部分:知识要点11、我们把实物中抽象的各种图形统称为几何图形。
几何图形分为立体图形和平面图形。
2、有些几何图形<如长方体、正方体、圆柱、圆锥、球等)的各部分不都在同一平面内,它们是立体图形。
3、有些几何图形<如线段、角、三角形、长方形、圆等)的各部分都在同一平面内,它们是平面图形。
4、将由平面图形围成的立体图形表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图。
b5E2RGbCAP5、长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等都是几何体。
几何体简称为体。
6、包围着体的是面,面有平的面和曲的面两种。
7、面与面相交的地方形成线<线有直的和曲的),线和线相交的地方是点<点无大小之分)。
8、点动成线,线动成面,面动成体。
9、几何图形都是由点、线、面、体组成的,点是构成图形的基本元素。
10、正方体的11种展开图:①“141型”,中间一行4个作侧面,上下两个各作为上下底面,•共有6种基本图形。
②“132型”,中间3个作侧面,共3种基本图形。
③“222型”,两行只能有1个正方形相连。
④、“33型”,两行只能有1个正方形相连。
11、经过两点有一条直线,并且只有一条直线。
简述为:两点确定一条直线<公理)。
12、当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点。
13、射线和线段都是直线的一部分。
14、点M把线段AB分成相等的两条线段AM和MB,点M叫做线段AB的中点。
15、两点的所有连线中,线段最短。
简单说成:两点之间,线段最短。
<公理)16、连接两点间的线段的长度,叫做这两点的距离。
17、一般地,用一个大写字母表示一个点,用两个大写字母<也就是两个点)或者一个小写字母来表示直线。
18、有公共端点的两条射线组成的图形叫做角,这个公共端点是角的顶点,这两条射线是角的两条边。
19、把一个周角360等分,每一份就是1度的角,记作1°;把一度的角60等分,每一份叫做1分的角,记作1′;把1分的角60等分,每一份叫做1秒的角,记作1″。
p1EanqFDPw20、角的度、分、秒是60进制的。
21、以度、分、秒为单位的角的度量制,叫做角度制。
22、从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线。
个人收集整理资料, 仅供交流学习, 勿作商业用途23、如果两个角的和等于90°<直角),就是说这两个叫互为余角,即其中的每一个角是另一个角的余角。
24、如果两个角的和等于180°<平角),就说这两个角互为补角,即其中一个角是另一个角的补角。
25、等角的补角相等,等角的余角相等。
知识要点2<1)、在几何里,我们常用字母表示图形。
如四边形ABCD <2)、一个点可以用一个大写字母表示,如点A <3)、一条直线可以用一个小写字母表示或用直线上两个点的大写字母表示,如直线l,或者直线AB <4)、一条射线可以用一个小写字母表示或用端点和射线上另一点来表示<端点字母写在前面),如射线l ,射线ABDXDiTa9E3d <5)、一条线段可以用一个小写字母表示或用它的端点的两个大写字母来表示,如线段l,线段AB 3、点和直线的位置关系有两种: ① 点在直线上,或者说直线经过这个点② 点在直线外,或者说直线不经过这个点。
4、线段的性质 <1)线段公理:两点之间的所有连线中,线段最短。
<2)两点之间的距离:两点之间线段的长度,叫做这两点之间的距离。
RTCrpUDGiT <3)线段的中点到两端点的距离相等。
<4)线段的大小关系和它们的长度的大小关系是一致的。
<5)线段的比较:1.目测法 2.叠合法 3.度量法5PCzVD7HxA 5、线段的中点: 点M 把线段AB 分成相等的两条相等的线段AM 与BM ,点M 叫做线段AB 的中点。
M 是线段AB 的中点AM=BM=AB<或者AB=2AM=2BM )6、直线的性质 <1)直线公理:经过两个点有且只有一条直线。
<2)过一点的直线有无数条<3)直线是是向两方面无限延伸的,无端点,不可度量,不能比较大小。
<4)直线上有无穷多个点。
<5)两条不同的直线至多有一个公共点。
jLBHrnAILg 知识要点3 1、角:有公共端点的两条射线组成的图形叫做角,两条射线的公共端点叫做这个角的顶点,这两条射线叫做这个角的边。
或:角也可以看成是一条射线绕着它的端点旋转而成的。
xHAQX74J0X 2、平角和周角:一条射线绕着它的端点旋转,当终边和始边成一条直线时,所形成的角叫做平角。
终边继续旋转,当它又和始边重合时,所形成的角叫做周角。
LDAYtRyKfE 角的表示:①用数字表示单独的角,如∠1,∠2,∠3等。
②用小写的希腊字母表示单独的一个角,如∠α,∠β,∠γ,∠θ等。
③用一个大写英文字母表示一个独立<在一个顶点处只有一个角)的角,如∠B ,∠C 等。
④用三个大写英文字母表示任一个角,如∠BAD ,∠BAE ,∠CAE 等。
Zzz6ZB2Ltk 注意:用三个大写英文字母表示角时,一定要把顶点字母写在中间,边上的字母写在两侧。
3、用一副三角板,可以画出15°,30°,45°,60°,75°,90°,105°,120°,135°,150°,165°dvzfvkwMI1M A B4、角的度量<1)、角的度量有如下规定:把一个平角180等分,每一份就是1度的角,单位是度,用“°”表示,1度记作“1°”,n 度记作“n °”。
rqyn14ZNXI 把1°的角60等分,每一份叫做1分的角,1分记作“1’”。
把1’ 的角60等分,每一份叫做1秒的角,1秒记作“1””。
<2)、角的性质 ① 角的大小与边的长短无关,只与构成角的两条射线的幅度大小有关。
② 角的大小可以度量,可以比较 ③ 角可以参与运算。
5、角的平分线 从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线。
OB 平分∠AOC∠AOB=∠BOC=∠AOC<或者∠AOC=2∠AOB=2∠BOC )6、余角和补角 ① 如果两个角的和是一个直角,这两个角叫做互为余角,简称互余,其中一个角是另一个角的余角。
用数学语言表示为如果∠α+∠β=90°,那么∠α与∠β互余;反过来,如果∠α与∠β互余,那么∠α+∠β=90°EmxvxOtOco ② 如果两个角的和是一个平角,这两个角叫做互为补角,简称互补,其中一个角是另一个角的补角。
用数学语言表示为如果∠α+∠β=180°,那么∠α与∠β互补;反过来如果∠α与∠β互补,那么∠α+∠β=180°SixE2yXPq5③ 同角<或等角)的余角相等;同角<或等角)的补角相等。
7、对顶角 ① 一对角,如果它们的顶点重合,两条边互为反向延长线,我们把这样的两个角叫做互为对顶角,其中一个角叫做另一个角的对顶角。
6ewMyirQFL 注意:对顶角是成对出现的,它们有公共的顶点;只有两条直线相交时才能形成对顶角。
② 对顶角的性质:对顶角相等如图,∠1和∠4是对顶角,∠2和∠3是对顶角。
∠1=∠4,∠2=∠3 8、平行线:1、概念:在同一个平面内,不相交的两条直线叫做平行线。
平行用符号“∥”表示,如“AB ∥CD ”,读作“AB 平行于CD ”。
kavU42VRUs 注意:① 平行线是无限延伸的,无论怎样延伸也不相交。
② 当遇到线段、射线平行时,指的是线段、射线所在的直线平行。
2、平行线公理及其推论<1)、平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
<2)、推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
<3)、补充平行线的判定方法:① 平行于同一条直线的两直线平行。
② 在同一平面内,垂直于同一条直线的两直线平行。
y6v3ALoS89③ 平行线的定义。
9、垂直:<1)、两条直线相交成直角,就说这两条直线互相垂直。
其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
M2ub6vSTnP 直线AB ,CD 互相垂直,记作“AB ⊥CD ”<或“CD ⊥AB ”>,读作“AB 垂直于CD ”<或“CD 垂直于AB ”)。
0YujCfmUCw <2)、垂线的性质:1 2 3 4 1°=60’,1’=60”性质1:平面内,过一点有且只有一条直线与已知直线垂直。
性质2:直线外一点与直线上各点连接的所有线段中,垂线段最短。
简称:垂线段最短。
点到直线的距离:过A 点作l 的垂线,垂足为B 点,线段AB 的长度叫做点A 到直线l 的距离。
同一平面内,两条直线的位置关系:相交或平行。
eUts8ZQVRd 第二部分:重点题型总结及应用题型一计算几何图形的数量1.数直线条数例1 已知n(n ≥2>个点P1,P2,P3,…,Pn 在同一平面上,且其中没有任何三点在同一直线上.设Sn 表示过这n 个点中的任意2个点所作的所有直线的条数,显然,S2=1,S3=3,S4=6,S6=10,…,由此推断,Sn =.sQsAEJkW5T 2.数线段条数例2 如图4—4—1所示,C 、D 为线段AB 上的任意两点,那么图中共有多少条线段? 例3 小明在看书时发现这样一个问题:在一次聚会中,共有6人参加,如果每两人都握一次手,共握几次手呢?小明通过认真思考得出了答案.为了解决一般问题,小明设计了下列图表进行探究:GMsIasNXkA 参加人数2 3 4 5 … 握手示意图握手次数 1 2+1=3 3+2+1=6 4+3+2+1=10 …3.数直线分平面的块数例4 豆腐是我们生活中的常见食品,常被分割成长方体或正方体的小块出售.现请你用刀切豆腐,每次切三刀,能将豆腐切成多少块?TIrRGchYzg .题型二两角互补、互余定义及其性质的应用例5 一个角的补角是这个角的4倍,求这个角的度数.例6 如果一个角的补角是120°,那么这个角的余角是( >A.30° B.60° C.90° D.150°例7 根据补角的定义和余角的定义可知,10°的角的补角是170°,余角是80°;15°的角的补角是165°,余角是75°;32°的角的补角是148°,余角是58°.…. 观察以上各组数据,你能得出怎样的结论?请用任意角α代替题中的10°、15°、32°的角来说明你的结论.7EqZcWLZNX题型三角的有关运算例8 如图4—4—3所示,AB和CD都是直线,∠AOE=90°,∠3°=∠FOD,∠1=27°20′,lzq7IGf02E求∠2、∠3的度数.例9 如图4—4—4所示,OB、OC是∠AOD内任意两条射线,OM平分∠AOB,ON平分∠COD,若∠MON=α,∠BOC=β,用α、β表示∠AOD.zvpgeqJ1hk.例10 (1>用度、分、秒表示54.12°. (2>32°44′24″等于多少度? (3>计算:133°22′43″÷3.NrpoJac3v1方法总结角的有关运算是指角的单位换算和角的加、减、乘、除运算.角度制的单位是 60进制的,和计量时间的时、分、秒一样.加减时,要将度、分、秒分别相加、相减,分、秒逢60要进位,而相减不够时要借1作60;度、分、秒形式乘一个数时,要将度、分、秒分别乘这个数,分、秒逢60进位;度、分、秒形式除以一个数时,也是将度、分、秒分别除以这个数,不过要将高位的余数转化成低位,与原位上的数相加后再除以这个数.1nowfTG4KI题型四钟表的时针与分针夹角问题例11 15:25时钟面上时针和分针所构成的角是度.题型五图形的转化例12 下列图形中不是正方体的平面展开图的是( >例13 如图4—4—6所示,将标号为A、B、C、D的正方形沿图中虚线剪开后,得到标号为P、Q、M、N的四组图形,试按照“哪个正方形剪开后得到哪组图形”的对应关系填空:A与对应;B与对应;C与对应;D与对应.fjnFLDa5Zo题型六方位角例14如图4—4—7所示,我海军的两艘军舰(分别在A、B两处>同时发现了一艘敌舰,其中A舰发现它在北偏东15°的方向上,B舰发现它在东北方向上,试画出这艘敌舰的位置(用字母C表示>.tfnNhnE6e5思想方法归纳1.分类讨论思想分类讨论,就是对问题所给对象的条件、结论、图形等不能进行统一研究时,就需要将研究对象按某个标准分类,然后对每一类分别研究得出每一类的结论,最后综合各类结果得到整个问题的解答.注意分类时要做到按同一标准且不重不漏.HbmVN777sL 例1 已知线段AB=8cm,在直线AB上画线段BC,使它等于3cm,求线段AC的长.例2 经过任意三点中的两点共可以画出的直线条数是( >A.1或3 B.3 C.2 D.12.数形结合思想数形结合思想就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来,通过“以形助数”或“以数解形”,即通过抽象思维与形象思维的结合,可以使复杂问题简单化、抽象问题具体化,从而起到优化解题途径的目的,线段、直线、角的重要性质也都是通过数形结合的思想体现的.V7l4jRB8Hs例3 如图4—4—11所示放置的三角板,把三角板较长的直角边从水平状态开始,在平面上沿着直线BC滚动一周,求B点转动的角度.83lcPA59W93.转化思想解决一个问题,往往是由未知向已知转化,由陌生向熟悉转化,由复杂向简单转化,转化思想贯穿整个数学学习的始终.mZkklkzaaP例4 将下列选项中的平面图形绕直线l旋转一周,可以得到如图4—4—13所示立体图形的是( >中考热点聚焦考点1 线段考点突破:线段问题在中考题中一般难度不大,解题时要结合图形,认真分析,问题便会迎刃而解.例1 <2018广东佛山,12,3分)已知线段AB=6,若C为AB中点,则AC=.<2018广西崇左,5,2分)在修建崇钦高速公路时,有时需要将弯曲的道路改直,依据是.考点2 余角和补角考点突破:此类题在中考中的考查为基础性题目,一般为选择题或填空题,只要牢记余角和补角的定义,便能准确求解.AVktR43bpw例2 <2018清远,6,3分)已知∠α=35°,则∠α的余角是< )A.35°B.55°C.65°D.145°<2018•南通)已知∠α=20°,则∠α的余角等于70°.<2018福建福州,5,4分)下列四个角中,最有可能与70°角互补的角是< )A.B.C.D.例3 如果∠α=60°,那么∠α的余角的度数是( >A.30° B.60° C.90° D.120°30°角的补角是( >A.30°角 B.60°角 C.90°角 D.150°角考点3 钟表上的角度问题考点突破:此类题是近几年中考中的热点问题,考查形式为选择题或填空题.解决此类问题需明确:在钟表上,1分钟分针走6°,1小时时针走30°.ORjBnOwcEd 例4 从3时到6时,钟表的时针旋转角的度数是( >A.30° B.60° C.90° D.120°考点4 从不同方向看立体图形考点突破:从不同方向看立体图形是中考的热点问题,几乎每套中考题中都会出现,解决问题时应发挥空间想象能力,把立体图形转化为平面图形.2MiJTy0dTT 例5如图4—4—15所示四个几何体中,从上面看得到的平面图形是圆的几何体共有( >A.1个 B.2个 C.3个 D.4个例6如图4—4—16所示的几何体是由7个大小相同的小正方体组成的,该几何体从上面看得到的平面图形为( >gIiSpiue7A综合验收评估测试卷一、选择题1. 下列说法正确的是( >A.平角是一条直线B.周角是一条射线C.用2倍的放大镜看1 cm的线段,这条线段变成了2 cmD.用2倍的放大镜看30°的角,这个角变成了60°2.下列说法正确的是( >A.直线AB与直线BA不是同一条直线B.线段AB与线段BA不是同一条线段C.射线OA与射线AO不是同一条射线D.射线OA与射线AO是同一条射线3. 如图4—4—17所示,AB=CD,则AC与BD的大小关系是( >A.AC>BD B.AC=BD C.AC<BD D.不能确定4. 如果线段AB=6 cm,BC=5cm,那么A、C两点间的距离是( >A.1 cm B.5.5 cm C.11 cm D.11 cm或1 cm5. 若∠α的补角是42°,∠β的余角是52°,则∠α和∠β的大小关系是( >A.∠α>∠β B.∠α<∠β C.∠α=∠β D.不能确定6. 如图4—4—18所示,∠1=15°,∠AOC=90°,B、O、D三点在一条直线上,则∠3等于( >uEh0U1YfmhA.75° B.105°C.15° D.165°7. 一个角和它的补角的度数比为1∶8,则这个角的余角为( >A.10° B.20° C.70° D.80°8. 如图4—4—19所示,已知∠AOC=∠BOD=∠78°,∠BOC= 35°,则∠AOD等于( >IAg9qLsgBXA.113° B.121° C.156° D.86°二、填空题9. 29°30′=度,18.25°=度分秒.10. 15分钟时间,时钟上的时针转了度,分针转了度.11. 如图4—4—20所示,由点B观测点A的方向是.12. 一个画家有14个棱长为1M的正方体,他在地面上把它们摆成如图4—4—21所示的形式,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为.WwghWvVhPE三、解答题13. 请仔细观察如图4—4—22所示的折纸过程,然后回答下列问题:(1>求∠2的大小.(2>∠1与∠3有何关系?(3>∠1与∠AEC,∠3与∠BEF分别有何关系?14. 如图4—4—23所示,已知AC=CD=DB,AC=2AM,BN=BM,如果MN=5cm,求AB、CN的长.asfpsfpi4k15. 如图4—4—24所示,一只蚂蚁从O点出发,沿北偏东30°方向爬行2.5 cm,碰到障碍物B后,又沿西北方向爬行3 cm到达C处.ooeyYZTjj1(1>画出蚂蚁爬行的路线;(2>求∠OBC的度数;(3>测出线段OC的长度(精确到0.1 cm>.申明:所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。