第四章《图形初步认识》复习(一)

课题 第四章 图形认识初步复习（两课时）【复习目标】:1.直观认识立体图形，掌握平面图形（线段、射线、直线）的基本知识；2.掌握角的基本概念，能利用角的知识解决一些实际问题。

【复习重点】: 线段、射线、直线、角的性质和运用【复习难点】:角的运算与应用；空间观念建立和发展；几何语言的认识与运用。

【导学指导】一、知识结构复习过程 一、知识梳理1、对于各种各样物体，我们数学主要是关注的是物体的 、 和 。

2、从实物中抽象出的各种图形统称 ；在各种几何图形中，若各部分不都在同一平面内我们称它们为 ；若各部分都在同一平面内，我们称它们为 。

3、 点、线、面、体与几何图形的关系： 点动成 ，线动成 ，面动成 。

其中 是构成图形的基本元素。

4、填写表格：5、经过两点有 且一条直线，简述为： 。

6、线段的最短性描述为、简单说成： 。

7、连接两点间的线段的 ，叫做这两点的距离。

89、线段中点：线段上的一点把一条线段分成 ，这一点叫这条线段的中点。

类似的还可以将线段三等分、四等分。

C 几何语言表达：如图，∵C 是线段AB 的中点。

∴ 或 AB=2 =2此图中存在着的和差关系：平面图形从不同方向看立体图形 展开立体图形 平面图形 几何图形 立体图形直线、射线、线段 角 两点之间，线段最短 线段大小的比较 角的度量角的比较与运算余角和补角 角的平分线等角的补角相等 等角的余角相等 两点确定一条直线 BA21==AC（第15题）1，若一个立体图形的正视图、左视图都是长方形,俯视图圆，则这个图形可能 （ ） A ．圆柱 B 球 C 圆锥 D 三棱锥2．你看这位（ ）A ．圆柱B ．棱锥C ．圆锥D ．球3．如图是一个正方形盒的展开图，若在其中的三个正方形A 、B 、C 、内分别填入适当的数，使得它们折成正方形后相对的面上的两个数互为相反数，则填入正方形A 、B 、C 内的三个数依次为 （ ） A ．1，2-，0 B ．0，2-，1 C ．2-，0，1 D ．2-，1，0 4．下列图形经过折叠不能围成三棱柱的是（ ）5．小丽制作了一个对面图案均相同的正方体礼品盒（如下左图所示），则这个正方体礼品盒的平面展开图可能是（ ）6．（6分）如图，分别画出他们的三视图。

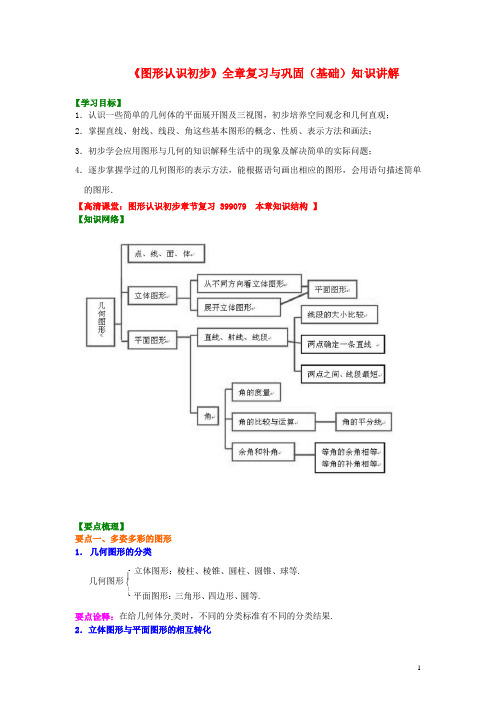
《图形认识初步》全章复习与巩固（基础）知识讲解【学习目标】1．认识一些简单的几何体的平面展开图及三视图，初步培养空间观念和几何直观； 2．掌握直线、射线、线段、角这些基本图形的概念、性质、表示方法和画法； 3．初步学会应用图形与几何的知识解释生活中的现象及解决简单的实际问题；4．逐步掌握学过的几何图形的表示方法，能根据语句画出相应的图形，会用语句描述简单的图形．【高清课堂：图形认识初步章节复习 399079 本章知识结构 】 【知识网络】【要点梳理】要点一、多姿多彩的图形 1． 几何图形的分类要点诠释：在给几何体分类时，不同的分类标准有不同的分类结果. 2．立体图形与平面图形的相互转化立体图形：棱柱、棱锥、圆柱、圆锥、球等. ⎧⎨⎩平面图形：三角形、四边形、圆等.几何图形⎧⎨⎩（1）立体图形的平面展开图：把立体图形按一定的方式展开就会得到平面图形，把平面图形按一定的途径进行折叠就会得到相应的立体图形，通过展开与折叠能把立体图形和平面图形有机地结合起来． 要点诠释：①对一些常见立体图形的展开图要非常熟悉，例如正方体的 11种展开图，三棱柱，圆柱等的展开图；②不同的几何体展成不同的平面图形，同一几何体沿不同的棱剪开，可得到不同的平面图形，那么排除障碍的方法就是：联系实物，展开想象，建立“模型”，整体构想，动手实践. （2）从不同方向看：主（正）视图---------从正面看 几何体的三视图 （左、右）视图-----从左（右）边看 俯视图---------------从上面看要点诠释：①会判断简单物体（直棱柱、圆柱、圆锥、球）的三视图. ②能根据三视图描述基本几何体或实物原型. （3）几何体的构成元素及关系几何体是由点、线 、面构成的.点动成线，线与线相交成点；线动成面，面与面相交成线；面动成体，体是由面组成. 要点二、直线、射线、线段1. 直线，射线与线段的区别与联系2. 基本性质(1)直线的性质:两点确定一条直线． (2)线段的性质:两点之间，线段最短． 要点诠释：①本知识点可用来解释很多生活中的现象. 如：要在墙上固定一个木条，只要两个钉子就可以了，因为如果把木条看作一条直线，那么两点可确定一条直线. ②连接两点间的线段的长度，叫做两点的距离. 3.画一条线段等于已知线段（1）度量法：可用直尺先量出线段的长度,再画一条等于这个长度的线段. （2）用尺规作图法：用圆规在射线AC 上截取AB=ａ，如下图：4．线段的比较与运算 （1）线段的比较：比较两条线段的长短，常用两种方法，一种是度量法；一种是叠合法. （2）线段的和与差：如下图，有AB+BC=AC ，或AC=a+b ；AD=AB-BD 。

图形的初步认识复习3.图形变换思想。

在研究⾓的概念时，要充分体会对射线旋转的认识。

在处理图形时应注意转化思想的应⽤，如⽴体图形与平⾯图形的互相转化。

4.化归思想。

在进⾏直线、线段、⾓以及相关图形的计数时，总要划归到公式n(n-1)/2的具体运⽤上来。

⼀、本章的知识结构图⼆、知识回顾本章的主要内容是图形的初步认识，从⽣活周围熟悉的物体⼊⼿，对物体的形状的认识从感性逐步上升到抽象的⼏何图形。

通过从不同⽅向看⽴体图形和展开⽴体图形，初步认识⽴体图形与平⾯图形的联系。

在此基础上，认识⼀些简单的平⾯图形——直线、射线、线段和⾓。

⼀、⽴体图形与平⾯图形例1 （1）如图1所⽰，上⾯是⼀些具体的物体，下⾯是⼀些⽴体图形，试找出与下⾯⽴体图形相类似的物体。

（2）如图2所⽰，写出图中各⽴体图形的名称。

图1图2解：（1）①与d类似，②与c类似，③与a类似，④与b类似。

（2）①圆柱，②五棱柱，③四棱锥，④长⽅体，⑤五棱锥。

例2 如图3所⽰，讲台上放着⼀本书，书上放着⼀个粉笔盒，指出右边三个平⾯图形分别是左边⽴体图形的哪个视图。

图3解：（1）左视图，（2）俯视图，（3）正视图练习1．下图是⼀个由⼩⽴⽅体搭成的⼏何体由上⽽看得到的视图，⼩正⽅形中的数字表⽰该位置⼩⽴⽅块的个数，则从正⾯看它的视图为（）2．如图，把左边的图形折叠起来，它会变成右边的正⽅体是右边的（）3．如图，下⾯三个正⽅体的六个⾯按相同规律涂有红、黄、蓝、⽩、⿊、绿六种颜⾊，那么涂黄⾊、⽩⾊、红⾊的对⾯分别是（）A．蓝、绿、⿊ B．绿、蓝、⿊ C．绿、⿊、蓝 D．蓝、⿊、绿4．若如下平⾯展开图折叠成正⽅体后，相对⾯上的两个数之和为5，求x＋y＋z的值。

5．⼀个物体从不同⽅向看的视图如下，画出该物体的⽴体图形。

⼆、直线、射线、线段（⼀）.直线、射线、线段的区别与联系：从图形上看，直线、射线可以看做是线段向两边或⼀边⽆限延伸得到的，或者也可以看做射线、线段是直线的⼀部分；线段有两个端点，射线有⼀个端点，直线没有端点；线段可以度量，直线、射线不能度量。