第23例材料蠕变分析实例

蠕变定义根据实验研究发现处于一定温度及定值静应力作用下，材料的变形将随着时间的延续而不断地慢慢增长，这一现象称为材料的蠕变。

它与塑性变形不同，塑蠕变曲线性变形通常在应力超过弹性极限之后才出现，而蠕变只要应力的作用时间相当长，它在应力小于弹性极限时也能出现。

金属、高分子材料和岩石等在一定条件下都具有蠕变性质。

蠕变材料的瞬时应力状态不仅与瞬时变形有关，而且与该瞬时以前的变形过程有关。

瞬时响应后随时间发展的蠕变一般可分成3个阶段：第一阶段是衰减蠕变，应变率（应变的时间变化率）随时间增加而逐渐减小；第二阶段是定常蠕变，应变率近似为常值；第三阶段是加速蠕变，应变率随时间逐渐增加，最后导致蠕变断裂。

同一材料在不同的应力水平或不同温度下，可处在不同的蠕变阶段。

通常温度升高或应力增大会使蠕变加快。

不同材料的蠕变微观机制不同。

引起多晶体材料蠕变的原因是原子晶间位错引起的点阵滑移以及晶界扩散等；而聚合物的蠕变机理则是高聚物分子在外力长时间作用下发生的构形和位移变化。

研究材料的蠕变性质对安全而经济地设计结构和机械零件具有重要意义。

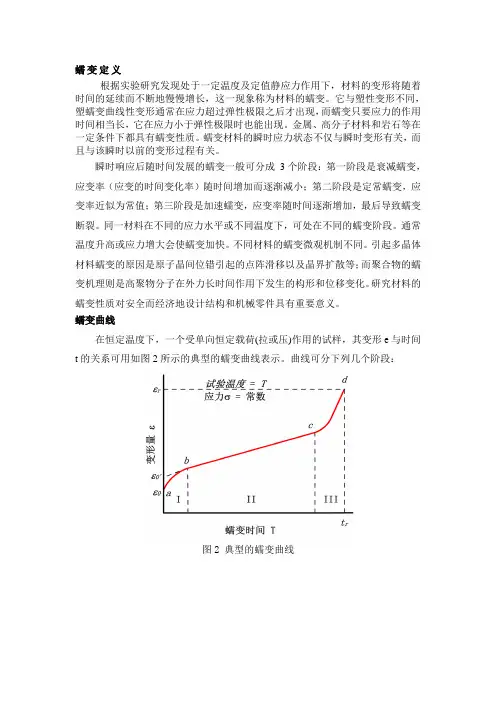
蠕变曲线在恒定温度下，一个受单向恒定载荷(拉或压)作用的试样，其变形e与时间t的关系可用如图2所示的典型的蠕变曲线表示。

曲线可分下列几个阶段：图2 典型的蠕变曲线第I阶段：减速蠕变阶段(图中AB段)，在加载的瞬间产生了的弹性变形e0，以后随加载时间的延续变形连续进行，但变形速率不断降低；第II阶段：恒定蠕变阶段，如图中曲线BC段，此阶段蠕变变形速率随加载时间的延续而保持恒定，且为最小蠕变速率；第III阶段：曲线上从C点到D点断裂为止，也称加速蠕变阶段，随蠕变过程的进行，蠕变速率显著增加，直至最终产生蠕变断裂。

D点对应的tr就是蠕变断裂时间，er是总的蠕变应变量。

温度和应力也影响蠕变曲线的形状。

在低温(<0.3Tm)、低应力下(曲线1)实际上不存在蠕变第III阶段，而且第II阶段的蠕变速率接近于零；在高温(>0.8Tm)、高应力下(曲线3)主要是蠕变第III阶段，而第II阶段几乎不存在。

材料的蠕变机制了解材料在高温下的变形机制材料的蠕变机制：了解材料在高温下的变形机制材料的蠕变（Creep）是指在高温和应力作用下，材料会逐渐发生形变和软化的现象。

蠕变机制的了解对于材料在高温环境下的设计和应用非常重要。

本文将探讨材料在高温下的变形机制，以及蠕变现象对材料性能的影响。

1. 引言随着工程领域对材料性能要求的提高，对于材料在极端条件下的变形行为的研究变得愈发重要。

高温下材料的蠕变现象是一项关键的考察对象，本文旨在深入探讨材料在高温环境下的变形机制，并分析其对工程应用的意义。

2. 材料在高温下的变形机制2.1 晶体滑移晶体滑移是一种经典的材料变形机制，在高温条件下尤其突出。

晶体原子通过在晶格面上滑移来改变位置，从而导致材料的塑性变形。

高温会增加晶体内的原子动能，使得晶体滑移更容易发生。

2.2 相互扩散在高温下，材料中的原子会因为动能提高而显示出相互扩散的特性。

相互扩散会导致晶界和晶体内部的松弛，进而引起材料的蠕变变形。

2.3 晶体再结晶晶体在高温和应力作用下可能发生再结晶，即原本晶体中的晶粒重新排列和重组。

这种再结晶过程也是材料蠕变的一个重要机制。

3. 蠕变对材料性能的影响3.1 强度和韧性的降低材料蠕变使得材料在高温下的强度和韧性均降低。

原子的扩散会导致材料晶界的松弛，晶体结构的破坏以及晶粒的再结晶，这些因素会使材料的强度降低。

3.2 变形速率蠕变行为与应力的大小、温度的高低以及时间的长短密切相关。

蠕变变形速率随温度的升高而增加，随应力的增加而加快。

这对一些高温工程应用中材料的耐久性和设计有着重要影响。

4. 变形机制的研究与应用4.1 实验方法通过高温实验设备对材料进行蠕变试验，可以模拟材料在高温下的变形行为。

通过测量变形曲线、变形速率和变形温度等参数，可以获取材料的蠕变特性。

4.2 材料改进与设计通过深入研究材料的蠕变机制，可以针对不同的应用需求改进和设计材料。

例如，在航空航天领域，对发动机叶片等高温结构部件材料的蠕变机制进行研究，以提高其抗蠕变性能。

高温环境下材料热蠕变行为的力学分析热蠕变是指在高温环境下，材料受到温度的变化而产生的形变现象。

在高温环境下，材料的原子或分子会发生较大幅度的热运动，导致材料发生蠕变变形。

理解和分析高温环境下材料的热蠕变行为对材料的设计和工程应用非常重要。

本文将进行力学分析，探讨高温环境下材料热蠕变行为的机制和影响因素。

首先，高温环境下材料热蠕变主要受到温度和应力的共同作用。

温度是引起热蠕变的主要原因，因为高温会使材料内部原子或分子的热运动剧烈增加。

而应力则是对材料施加的外部力，使材料发生变形。

热蠕变行为的机制可以分为几个方面：首先是晶粒滑移。

在高温下，材料的晶界可以发生滑移，从而使材料产生变形。

晶界滑移是材料热蠕变的主要机制之一，晶界的运动和滑移会导致材料局部发生变形。

其次是晶粒的生长和再结晶。

高温环境下，晶粒可以通过长大和再结晶来调整材料的组织结构，从而减小材料的变形和蠕变行为。

晶粒生长和再结晶可以优化材料的力学性能，减弱材料的蠕变行为。

此外，扩散也是高温热蠕变的机制之一。

材料中的原子或分子在高温下可以通过扩散移动，从而导致材料的蠕变行为。

扩散对材料的蠕变变形具有重要影响，可以导致材料发生局部变形和形状变化。

掌握材料热蠕变行为的力学分析方法可以更好地进行材料设计和应用。

具体的力学分析包括以下几个方面：首先是材料的热弹性性能分析。

热弹性性能是指材料在高温下的应力-应变行为。

通过测量材料在不同温度下的力学性能，可以确定材料的热蠕变特性和材料参数，从而提供材料设计和应用的依据。

其次是材料的蠕变行为建模和预测。

通过建立材料的蠕变行为数学模型，可以预测材料在高温环境下的蠕变变形和寿命。

常用的模型包括Norton、Bailey-Norton 和Manson-Haferd等模型，这些模型可以用于预测材料的蠕变变形和寿命，从而指导材料的设计和应用。

此外，热蠕变行为的力学分析还包括材料的应力松弛分析、材料的蠕变裂纹扩展分析等。

蠕变定义根据实验研究发现处于一定温度及定值静应力作用下，材料的变形将随着时间的延续而不断地慢慢增长，这一现象称为材料的蠕变。

它与塑性变形不同，塑蠕变曲线性变形通常在应力超过弹性极限之后才出现，而蠕变只要应力的作用时间相当长，它在应力小于弹性极限时也能出现。

金属、高分子材料和岩石等在一定条件下都具有蠕变性质。

蠕变材料的瞬时应力状态不仅与瞬时变形有关，而且与该瞬时以前的变形过程有关。

瞬时响应后随时间发展的蠕变一般可分成3个阶段：第一阶段是衰减蠕变，应变率（应变的时间变化率）随时间增加而逐渐减小；第二阶段是定常蠕变，应变率近似为常值；第三阶段是加速蠕变，应变率随时间逐渐增加，最后导致蠕变断裂。

同一材料在不同的应力水平或不同温度下，可处在不同的蠕变阶段。

通常温度升高或应力增大会使蠕变加快。

不同材料的蠕变微观机制不同。

引起多晶体材料蠕变的原因是原子晶间位错引起的点阵滑移以及晶界扩散等；而聚合物的蠕变机理则是高聚物分子在外力长时间作用下发生的构形和位移变化。

研究材料的蠕变性质对安全而经济地设计结构和机械零件具有重要意义。

蠕变曲线在恒定温度下，一个受单向恒定载荷(拉或压)作用的试样，其变形e与时间t的关系可用如图2所示的典型的蠕变曲线表示。

曲线可分下列几个阶段：图2 典型的蠕变曲线第I阶段：减速蠕变阶段(图中AB段)，在加载的瞬间产生了的弹性变形e0，以后随加载时间的延续变形连续进行，但变形速率不断降低；第II阶段：恒定蠕变阶段，如图中曲线BC段，此阶段蠕变变形速率随加载时间的延续而保持恒定，且为最小蠕变速率；第III阶段：曲线上从C点到D点断裂为止，也称加速蠕变阶段，随蠕变过程的进行，蠕变速率显著增加，直至最终产生蠕变断裂。

D点对应的tr就是蠕变断裂时间，er是总的蠕变应变量。

温度和应力也影响蠕变曲线的形状。

在低温(<0.3Tm)、低应力下(曲线1)实际上不存在蠕变第III阶段，而且第II阶段的蠕变速率接近于零；在高温(>0.8Tm)、高应力下(曲线3)主要是蠕变第III阶段，而第II阶段几乎不存在。

4.4蠕变分析4.4.1 蠕变理论4.4.1.1 定义蠕变是率相关材料非线性，即在常荷载作用下，材料连续变形的特性。

相反如果位移固定，反力或应力将随时间而变小，这种特性有时也称为应力松驰，见图4-18a。

图4-18应力松弛和蠕变蠕变的三个阶段如图4-18b所示。

在初始蠕变阶段，应变率随时间而减小，这个阶段一般发生在一个相当短的时期。

在第二期蠕变阶段，有一个常应变率，所以应变以常速率发展，在第三期蠕变阶段，应变率迅速增加直到材料失效。

由于第三期蠕变阶段所经历的时间很短，材料将失效，所以通常情况下，我们感兴趣的是初始蠕变和第二期蠕变。

ANSYS程序中的蠕变行为用来模拟初始蠕变和第二期蠕变。

蠕变系数可以是应力、应变、温度、时间或其它变量的函数。

在高温应力分析中(如核反应堆等)，蠕变分析非常重要。

例如，假设在核反应堆中施加了预荷载，以保证与相邻部件保持接触而不松开。

在高温下过了一段时间后，预荷载将降低(应力松驰)，可能使接触部件松开。

对于一些材料如预应力砼，蠕变也可能十分重要。

最重要的是要记住，蠕变是永久变形。

4.4.1.2 理论介绍蠕变方程：我们通过一个方程来模拟蠕变行为，此方程描述了在实验中观测到的主要特征（特别是在一维的拉伸实验中）。

这个方程以蠕应变率的方式表示出来，其形式如下：上式中，A、B、C、D是从实验中得到的材料常数，常数本身也可能是应力，应变，时间或温度的函数，这种形式的方程被称为状态方程。

上式中，当常数D为负值时，蠕应变率随时间下降，材料处于初始蠕变阶段，当D为0时，蠕应变率为常值，材料处于第二期蠕变阶段。

对于2－D或3－D应力状态，使用VON Mises方程计算蠕应变率方程中所使用的标量等效应力和等效应变。

对蠕变方程积分时，我们使用经过修改的总应变，其表达式为:经过修改的等效总应变为:其等效应力由下式算出：其中：G=剪切模量＝等效蠕应变增量由程序给出的某一种公式进行计算，一般为正值，如果在数据表中，则使用的是衰减的蠕应变率而不是常蠕变率，但这个选项一般不被推荐，因为在初始蠕变所产生的应力为主的情况下，它可能会严重的低估蠕变值。

高温环境下的材料蠕变行为分析高温环境下的材料蠕变行为是指在高温条件下，材料长期受到恒定应力或变应力作用下产生的时间依赖性塑性变形现象。

蠕变行为在工程设计、材料选择和材料寿命评估等方面具有重要的意义。

本文将分析高温环境下材料蠕变行为的原因及其对材料性能的影响。

首先，高温环境下材料蠕变行为的原因可以归结为材料内部的结构变化和界面扩散。

材料内部的结构变化主要包括晶格的位错运动和晶胞的形变。

在高温下，材料中的晶体结构受到热振动的影响，晶格上的位错会发生滑动、蠕变和爬行等运动，从而引起材料的塑性变形。

此外，高温下晶胞的形变也会造成材料的蠕变。

界面扩散是指材料内部原子或分子的迁移和固态扩散。

在高温条件下，原子或分子的活动性增加，扩散速率加快，导致材料的界面扩散现象增强。

界面扩散的结果是材料的晶粒长大、粒界清晰度降低以及晶体之间的结合强度减弱等，从而影响材料的力学性能。

其次，高温环境下的材料蠕变行为会对材料的性能产生一系列影响。

首先，蠕变会导致材料的变形。

高温环境下，由于长期受到应力作用，材料会发生塑性变形，产生蠕变。

蠕变不仅会改变材料的形状，还会导致材料的尺寸稳定性降低，形成材料的塌陷或组织结构的变形。

其次，蠕变会影响材料的力学性能。

高温蠕变引起的变形会导致材料的应力应变曲线产生漂移，降低材料的强度、韧性和抗疲劳性能。

此外，蠕变还会引起材料内部的显微结构损伤，如晶粒的长大、晶界断裂等，进一步降低材料的力学性能。

再次，蠕变会影响材料的寿命。

高温环境下的长期蠕变会引起材料的老化和疲劳，加速材料的疲劳破坏过程。

蠕变还会引起材料内部的应力分布不均匀，导致应力集中和裂纹的形成，进而降低材料的寿命。

最后，为了应对高温环境下的材料蠕变行为，可以采取以下措施。

首先，选择合适的材料。

在高温环境下，要选择具有良好抗蠕变性能的材料，如耐高温合金、陶瓷材料等。

这些材料具有较高的熔点和热稳定性，能够在高温下保持较好的力学性能。

其次，采用适当的工艺措施。

沥青蠕变案例嘿，咱来说说这个沥青蠕变的案例哈。

沥青这东西呢，在咱们的日常生活里可太常见了，像马路上的柏油马路啥的好多都是沥青铺的。

这个案例就是在一个特定的工程里发生的，具体是啥工程呢，就是一个比较大型的公路建设工程啦。

这个工程所在的地方气候有点复杂，夏天的时候超热，冬天的时候又冷得不行。

而且这个地方车流量还挺大的，对路面的压力不小呢。

二、问题详细描述那这个沥青就出问题啦。

沥青出现了蠕变现象，啥是蠕变呢？就是这个沥青在长期受到压力和温度变化的影响下，它就慢慢变形了。

你想啊，马路上的沥青变形了那可不得了。

路面就开始变得不平整了，有好多坑坑洼洼的地方。

汽车在上面走的时候，就像坐过山车似的，一颠一颠的。

这不仅影响了行车的舒适度，还存在安全隐患呢，万一因为路面不平导致车辆失控啥的，那可就糟了。

三、解决方案概述那肯定得想办法解决呀。

就打算对这个沥青路面进行修复和加固。

一种方法呢是在原来的沥青路面上再铺一层新的沥青，这就像是给路面穿了一件新衣服一样。

还有就是对路面进行一些特殊的处理，让沥青能够更好地抵抗压力和温度的变化。

四、实施步骤细节1. 首先得把路面清理干净，不能有杂物啥的。

那些小石子啊，灰尘啊，都得清掉。

就像咱们打扫房间一样，得把地扫干净了才能在上面铺东西嘛。

2. 然后开始准备新的沥青材料，这个沥青材料可得选好喽，要那种质量好的，能够适应这个地方的气候条件的。

3. 接着就开始铺新的沥青了，铺的时候得注意均匀，不能有的地方厚有的地方薄。

4. 在铺完沥青之后呢，还要用一些特殊的工具把路面压实，让沥青紧紧地贴在路面上。

五、成果与效果评估经过这么一番折腾之后呢，路面确实变得平整多了。

汽车在上面走的时候也平稳了。

从安全方面来说，也减少了很多因为路面不平而产生的风险。

而且经过一段时间的观察，发现这个新的沥青路面能够较好地抵抗温度和压力的变化，没有再出现明显的蠕变现象了。

六、遇到的问题与解决1. 在清理路面的时候，发现有些污渍特别难清理，就用了一些特殊的清洁剂来处理，费了好大的劲儿才把路面清理干净。

材料的蠕变性能研究及其应用材料的蠕变性能是指材料在长时间高温和持续应力下可能发生的形变现象。

它在工程设计和材料选择中具有重要的意义。

本文将分析材料的蠕变性能研究，探讨其应用领域，并介绍一些相关的实例。

一、蠕变性能研究1. 影响蠕变的因素材料的蠕变性能受多种因素的影响，包括温度、应力、加载时间和材料的化学成分等。

温度是蠕变的主要驱动力，高温会导致材料晶体结构发生改变，从而引起形变。

应力是指材料所受到的外力，而加载时间则是指在一定的温度和应力下所作用的时间。

2. 蠕变性能的测试方法为了研究材料的蠕变性能，科学家们发展了一系列的测试方法。

其中最常见的方法是蠕变实验，通过在高温下对材料施加恒定的力来观察其变形情况。

此外，还有一些间接的测试方法，如热蠕变微观分析和差热分析等。

3. 提高蠕变抗力的方法考虑到材料在高温和应力环境下可能发生的蠕变，科学家们还提出了一系列的方法来提高材料的蠕变抗力。

例如，通过控制材料的成分和晶体结构来提高其抗蠕变能力。

此外，采用表面涂层和添加合适的合金元素也可以改善材料的蠕变性能。

二、蠕变性能的应用1. 高温材料蠕变性能的研究对于高温材料的选择和改良具有重要的意义。

例如，在航空发动机和核能设备等高温环境中，需要使用能够承受长时间高温和持续应力的材料。

通过研究材料的蠕变性能，可以选择出适合特定环境的高温材料，并进行进一步的改良。

2. 地质工程在地质工程中，蠕变性能的研究也具有重要的应用价值。

例如，在地下隧道的建设过程中，需要选择能够承受地下高温和持续应力的材料，以确保隧道的安全性和稳定性。

通过对材料的蠕变性能进行研究，可以为地质工程提供重要的参考依据。

3. 材料设计材料的蠕变性能也对于材料的设计和开发具有指导意义。

通过研究材料的蠕变行为，可以优化材料的组成和结构，以提高其抗蠕变能力。

在材料开发过程中，这种研究方法可以帮助科学家们选择最合适的材料，并对其进行优化设计。

三、实际应用案例1. 航空发动机航空发动机工作时处于高温高压环境下，材料的蠕变性能对其工作性能和寿命有着重要影响。

蠕变分析4.4.1 蠕变理论4.4.1.1 定义蠕变是率相关材料非线性，即在常荷载作用下，材料连续变形的特性。

相反如果位移固定，反力或应力将随时间而变小，这种特性有时也称为应力松驰，见图4-18a。

图4-18 应力松弛和蠕变蠕变的三个阶段如图4-18b所示。

在初始蠕变阶段，应变率随时间而减小，这个阶段一般发生在一个相当短的时期。

在第二期蠕变阶段，有一个常应变率，所以应变以常速率发展，在第三期蠕变阶段，应变率迅速增加直到材料失效。

由于第三期蠕变阶段所经历的时间很短，材料将失效，所以通常情况下，我们感兴趣的是初始蠕变和第二期蠕变。

ANSYS程序中的蠕变行为用来模拟初始蠕变和第二期蠕变。

蠕变系数可以是应力、应变、温度、时间或其它变量的函数。

在高温应力分析中(如核反应堆等)，蠕变分析非常重要。

例如，假设在核反应堆中施加了预荷载，以保证与相邻部件保持接触而不松开。

在高温下过了一段时间后，预荷载将降低(应力松驰)，可能使接触部件松开。

对于一些材料如预应力砼，蠕变也可能十分重要。

最重要的是要记住，蠕变是永久变形。

4.4.1.2 理论介绍蠕变方程：我们通过一个方程来模拟蠕变行为，此方程描述了在实验中观测到的主要特征（特别是在一维的拉伸实验中）。

这个方程以蠕应变率的方式表示出来，其形式如下：上式中，A、B、C、D是从实验中得到的材料常数，常数本身也可能是应力，应变，时间或温度的函数，这种形式的方程被称为状态方程。

上式中，当常数D为负值时，蠕应变率随时间下降，材料处于初始蠕变阶段，当D为0时，蠕应变率为常值，材料处于第二期蠕变阶段。

对于2－D或3－D应力状态，使用VON Mises方程计算蠕应变率方程中所使用的标量等效应力和等效应变。

对蠕变方程积分时，我们使用经过修改的总应变，其表达式为:经过修改的等效总应变为:其等效应力由下式算出：其中：G=剪切模量＝等效蠕应变增量由程序给出的某一种公式进行计算，一般为正值，如果在数据表中，则使用的是衰减的蠕应变率而不是常蠕变率，但这个选项一般不被推荐，因为在初始蠕变所产生的应力为主的情况下，它可能会严重的低估蠕变值。