ansys高级非线性分析四蠕变教学文案

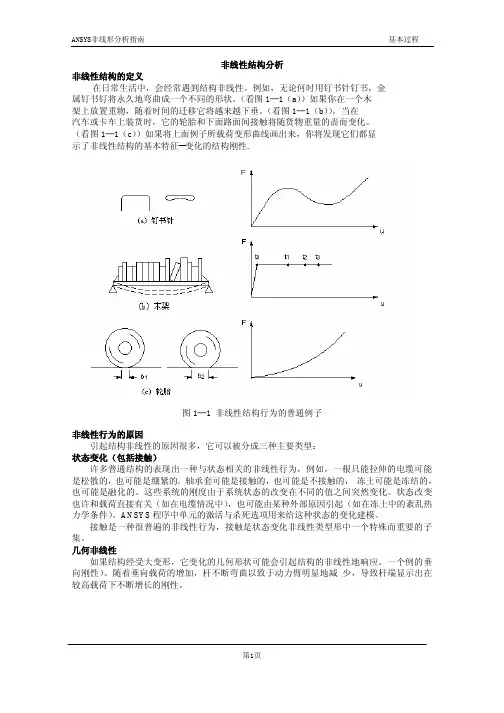
非线性结构分析非线性结构的定义在日常生活中，会经常遇到结构非线性。

例如，无论何时用钉书针钉书，金属钉书钉将永久地弯曲成一个不同的形状。

（看图1─1（a））如果你在一个木架上放置重物，随着时间的迁移它将越来越下垂。

（看图1─1（b））。

当在汽车或卡车上装货时，它的轮胎和下面路面间接触将随货物重量的啬而变化。

（看图1─1（c））如果将上面例子所载荷变形曲线画出来，你将发现它们都显示了非线性结构的基本特征--变化的结构刚性.图1─1 非线性结构行为的普通例子非线性行为的原因引起结构非线性的原因很多，它可以被分成三种主要类型：状态变化（包括接触）许多普通结构的表现出一种与状态相关的非线性行为，例如，一根只能拉伸的电缆可能是松散的，也可能是绷紧的。

轴承套可能是接触的，也可能是不接触的，冻土可能是冻结的，也可能是融化的。

这些系统的刚度由于系统状态的改变在不同的值之间突然变化。

状态改变也许和载荷直接有关（如在电缆情况中），也可能由某种外部原因引起（如在冻土中的紊乱热力学条件）。

ANSYS程序中单元的激活与杀死选项用来给这种状态的变化建模。

接触是一种很普遍的非线性行为，接触是状态变化非线性类型形中一个特殊而重要的子集。

几何非线性如果结构经受大变形，它变化的几何形状可能会引起结构的非线性地响应。

一个例的垂向刚性）。

随着垂向载荷的增加，杆不断弯曲以致于动力臂明显地减少，导致杆端显示出在较高载荷下不断增长的刚性。

图1─2 钓鱼杆示范几何非线性材料非线性非线性的应力──应变关系是结构非线性名的常见原因。

许多因素可以影响材料的应力──应变性质，包括加载历史（如在弹─塑性响应状况下），环境状况（如温度），加载的时间总量（如在蠕变响应状况下）。

牛顿一拉森方法ANSYS程序的方程求解器计算一系列的联立线性方程来预测工程系统的响应。

然而，非线性结构的行为不能直接用这样一系列的线性方程表示。

需要一系列的带校正的线性近似来求解非线性问题。

ANSYS教程，非线性结构分析过程尽管非线性分析比线性分析变得更加复杂，但处理基本相同。

只是在非线形分析的适当过程中，添加了需要的非线形特性。

非线性结构分析的基本分析过程也主要由建模、加载并求解和观察结果组成。

下面来讲解其主要步骤和各个选项的处理方法。

建模这一步对线性和非线性分析都是必需的，尽管非线性分析在这一步中可能包括特殊的单元或非线性材料性质，如果模型中包含大应变效应，应力─应变数据必须依据真实应力和真实（或对数）应变表示。

加载求解在建立好有限元模型之后，将进入ANSYS求解器(GUI：Main Menu | Solution)，并根据分析的问题指定新的分析类型(ANTYPE)。

求解问题的非线性特性在ANSYS中是通过指定不同的分析选项和控制选项来定义的。

非线性分析不同于线性分析之处在于，它通常要求执行多荷载步增量和平衡迭代。

下面就详细讲解一下进行非线性结构分析需要定义的各个求解选项、分析选项和控制选项是如何设置的，以及他们的意义是什么。

求解控制对于一些基本的非线性问题的分析选项，可以通过ANSYS提供的求解控制对话框中的选项设置来完成。

选择菜单路径：Main Menu | Solution | Analysis Type | Sol’n Controls，将弹出求解控制(Solution Controls)对话框，如下图所示。

从图中可以看出该对话框主要包括5个选项卡：基本选项（Basic）、瞬态选项（Transient）、求解选项（Sol’n Options）、非线性选项（Nonlinear）和高级非线性选项（Advanced NL）。

如果开始一项新的分析，在设置分析类型和非线性选项时，选择“Large Displacement Static”选项（不是所有的非线性分析都支持大变形）。

如果想要重新启动一个失败的非线性分析，则选择“Restart Current Analysis”选项。

选中下面的“Calculate prestress effects”单选按钮用于有预应力的模态分析时的预应力计算，具体内容见模态分析部分。

除去蠕变，这个模型的结果可靠性是不错的。

作了一系列接触问题，通过试验验证符合的很好。

模型解释：（1）一个弹性结构受压（接触）变形，到发生塑性变形。

（2）拿开压缩板，结构回弹，但不会回到原始位置。

（3）这时计算蠕变，释放掉应力。

（4）再压弹性结构到开始压缩位置。

比较这四步的接触力。

结果：第二，三步当然没有接触力，（若没有应力释放，第一、第四步接触力应一样，）有了应力释放，第四步接触力比第一步减小。

这个模型中的蠕变没用太好。

用的是隐式6号蠕变方程，蠕变是时间和应力的函数，参数是乱定的（应力释放太快）。

想请教有关蠕变方面的资料，尤其是材料蠕变方程选用及参数方面的资料。

/prep7!------------CuSn8----------ET,1,182,,,3mp,ex,1,115e9mp,prxy,1,0.3r,1,0.3TB,BKIN,1TBDA TA,1,470E6,0tm=100*SET,C1,1.5625E-14      !ASSIGN VALUE*SET,C2,1.5        !ASSIGN V ALUE*SET,C3,        !ASSIGN V ALUE*SET,C4,0        !ASSIGN V ALUETB,CREEP,1,,,6        !ACTIV ATE DA TA TABLETBDA TA,1,C1,C2,C3,C4      !DEFINE DATA FOR TABLE!-----------contact-----------------ET,9,169ET,10,171R,9,,,0.1,0.1,,!RMORE,,,1.0E20,0.0,1.0,!RMORE,0.0,0,1.0,0,0,0.5!RMORE,,,1.0,0.0MP,MU,9,0.0!----------------geometryk,,2k,,2,0.2k,,,0.2k,,-0.2k,,-0.2,1.2k,,,1k,,2,1.2k,,1,1k,,1.25,1k,,2,1L,8,9,k,,1.5,1.2k,,1.75,1.45L, 1, 2 L, 1, 4 L, 4, 5 L, 5, 11larc,7,12,11,0.25 larc,11,12,7,0.25L, 7, 10 L, 10, 9 L, 8, 6 L, 6, 3 L, 3, 2LFILLT,11,10,0.3, ,!*LFILLT,4,5,0.5, ,!*LFILLT,11,12,0.3, ,!*LFILLT,4,3,0.5, ,FLST,2,16,4 FITEM,2,12 FITEM,2,15 FITEM,2,11 FITEM,2,13FITEM,2,10FITEM,2,1FITEM,2,9FITEM,2,8FITEM,2,7FITEM,2,6FITEM,2,5FITEM,2,14FITEM,2,4FITEM,2,16FITEM,2,3FITEM,2,2AL,P51Xrect,1,3,1.45+0.001,1.5type,1mat,1esize,0.05amesh,all!---------contact------------ allstype,10mat,9real,9lsel,s,,,6,7nsll,s,1esln,s,0esurf,alltype,9mat,9real,9lsel,s,,,17nsll,s,1esln,s,0esurf,all!------boundarylsel,s,,,3nsll,,1d,all,uxd,all,uylsel,s,,,19nsll,,1cp,11,uy,allcplgen,11,ux*get,nmin,node,,num,min d,nmin,uxksel,s,,,10nslk*get,ndis,node,,num,minfini/soluantype,staticnlgeom,onautots,onallssaverate,offtime,1e-8d,nmin,uy,-0.3nsub,20outres,all,allsolve*get,rf1,node,nmin,rf,fy *get,dis1,node,ndis,u,ytime,2e-8d,nmin,uy,0.0nsub,20outres,all,allsolve*get,rf2,node,nmin,rf,fy*get,dis2,node,ndis,u,y!BFUNIF,TEMP,90rate,onTIME,tm!NSUBST,10OUTPR,BASIC,10 ! PRINT BASIC SOLUTION FOR EVERY 10TH SUBSTEP OUTRES,ESOL,1 ! STORE ELEMENT SOLUTION FOR EVERY SUBSTEP SOLVE*get,rf3,node,nmin,rf,fy*get,dis3,node,ndis,u,yrate,offtime,tm+1e-8d,nmin,uy,-0.3nsub,20outres,all,allsolve*get,rf4,node,nmin,rf,fy*get,dis4,node,ndis,u,y/EOFtime,11d,nmin,uy,-0.0nsub,20outres,all,allsolve*get,rf11,node,nmin,rf,fy*get,dis11,node,ndis,u,y/eoffini/post1*get,rf2,node,nmin,rf,fy fini/eof。

01112121222y y d N d d R d M d d R ελφ⎧⎫
⎧⎫⎡⎤⎧⎫=∆+⎨⎬⎨⎬⎨⎬⎢⎥
⎣⎦⎩⎭
⎩⎭⎩⎭ 改写为，
11112021222y y d N R d d d d M R d d εφλ-⎡⎤⎧⎫⎧⎫
⎧⎫=-⎨⎬⎨⎬⎨⎬⎢⎥
-⎩⎭⎩⎭⎩⎭
⎣⎦ 求解过程中，可控制d φy 的值，求出相应的0d ε及荷载增量比例因子d λ。

由于ij d 与截面应变平面有关，需要迭代才能使截面补平衡力12,R R 趋近于零。

图4-9 位移控制法 在结构分析中控制指定位移增量，则P —δ曲线的下降段不难求得。

将底端固定顶端自由的柱，在柱顶端施加水平荷载，将柱的加载点处换为支座，而分析时控制该支座位移并求出该支座的反力，图4—9表示了得到的全过程分析P-δ曲线。

对于一般结构，将刚度矩阵重新排列，使得选择的控制位移排到最后，将原矩阵分块表示成以下形式，
111211121
22222K K du P R K K du P R ⎡⎤⎧⎫⎧⎫⎧⎫=∆+⎨⎬⎨⎬⎨⎬⎢⎥⎣⎦⎩⎭⎩⎭⎩⎭
λ 改写方程为，
11
11121221
2222K P R K du du K P R K -⎡⎤⎧⎫⎧⎫⎧⎫
=-⎨⎬⎨⎬⎨⎬⎢⎥-∆⎩⎭⎣⎦⎩⎭⎩⎭
λ 需要指出的是，改写以后的系数矩阵是不对称的，也不是带状的，求解时需要较多的存储单元。

§4.5.4 修正完善后的弧长法 1．弧长法的基本原理
仍从结构增量平衡方程：{}{}{}11i i i i K w P g --=-∆∆λ∆。

ANSYS高级非线性分析四蠕变简介蠕变是物质受力作用下的长时间形变现象。

在工程领域中，蠕变是一个重要的现象，因为它可能导致结构疲劳、失效以及安全问题。

在工程设计中，了解和预测材料蠕变行为是非常重要的，特别是在高温环境下。

在这方面，ANSYS提供了强大的高级非线性分析工具，可以模拟和预测材料的蠕变行为。

ANSYS高级非线性分析ANSYS是一款流行的有限元分析软件，广泛应用于工程领域。

在高级非线性分析中，ANSYS可以模拟材料的非线性行为，包括蠕变。

蠕变分析是一种长时间的形变分析，可以用来评估材料和结构在高温条件下的稳定性。

ANSYS的高级非线性分析功能可以通过几个步骤来实现。

首先，需要定义材料的力学性质，包括弹性模量、屈服强度和蠕变参数等。

其次，需要定义结构的几何形状和边界条件。

然后，可以设置加载条件，包括时间和温度的变化。

最后，可以进行蠕变分析，并输出结果。

四蠕变四蠕变是一种特殊的蠕变现象，出现在某些金属材料中。

四蠕变是指材料在连续加载下显示出四个明显的蠕变阶段，其形变速率逐渐增加，并最终稳定在一个较高的速率上。

这种蠕变现象对于结构设计和材料选择具有重要意义。

ANSYS可以模拟和分析四蠕变现象。

在进行四蠕变分析时，需要输入材料的蠕变参数。

这些参数可以通过试验或经验获得。

通过分析材料的力学性质和加载条件，可以获得材料的蠕变行为，并预测材料在长时间形变下的稳定性。

ANSYS高级非线性分析四蠕变的应用ANSYS高级非线性分析四蠕变在工程设计中具有广泛的应用。

以下列举了几个常见的应用领域：1. 高温结构设计在高温条件下，材料的蠕变行为是一个重要的考虑因素。

使用ANSYS高级非线性分析四蠕变，可以模拟和预测高温结构的蠕变行为，从而在结构设计中选择合适的材料和几何形状。

2. 轴承和齿轮设计轴承和齿轮是机械系统中常见的零件，需要承受高强度和高载荷。

使用ANSYS高级非线性分析四蠕变，可以评估轴承和齿轮材料的蠕变行为，从而选择合适的材料和结构参数。

ANSYS结构⾮线性分析指南（⼀⾄三章）ANSYS结构⾮线性分析指南(⼀到三章)屈服准则概念：1.理想弹性材料物体发⽣弹性变形时，应⼒与应变完全成线性关系，并可假定它从弹性变形过渡到塑性变形是突然的。

2.理想塑性材料（⼜称全塑性材料）材料发⽣塑性变形时不产⽣硬化的材料，这种材料在进⼊塑性状态之后，应⼒不再增加，也即在中性载荷时即可连续产⽣塑性变形。

3.弹塑性材料在研究材料塑性变形时，需要考虑塑性变形之前的弹性变形的材料这⾥可分两种情况：Ⅰ.理想弹塑性材料在塑性变形时，需要考虑塑性变形之前的弹性变形，⽽不考虑硬化的材料，也即材料进⼊塑性状态后，应⼒不再增加可连续产⽣塑性变形。

Ⅱ.弹塑性硬化材料在塑性变形时，既要考虑塑性变形之前的弹性变形，⼜要考虑加⼯硬化的材料，这种材料在进⼊塑性状态后，如应⼒保持不变，则不能进⼀步变形。

只有在应⼒不断增加，也即在加载条件下才能连续产⽣塑性变形。

4.刚塑性材料在研究塑性变形时不考虑塑性变形之前的弹性变形。

这⼜可分两种情况：Ⅰ.理想刚塑性材料在研究塑性变形时，既不考虑弹性变形，⼜不考虑变形过程中的加⼯硬化的材料。

Ⅱ.刚塑性硬化材料在研究塑性变形时，不考虑塑性变形之前的弹性变形，但需要考虑变形过程中的加⼯硬化材料。

屈服准则的条件：1.受⼒物体内质点处于单向应⼒状态时，只要单向应⼒⼤到材料的屈服点时，则该质点开始由弹性状态进⼊塑性状态，即处于屈服。

2.受⼒物体内质点处于多向应⼒状态时，必须同时考虑所有的应⼒分量。

在⼀定的变形条件（变形温度、变形速度等）下，只有当各应⼒分量之间符合⼀定关系时，质点才开始进⼊塑性状态，这种关系称为屈服准则，也称塑性条件。

它是描述受⼒物体中不同应⼒状态下的质点进⼊塑性状态并使塑性变形继续进⾏所必须遵守的⼒学条件，这种⼒学条件⼀般可表⽰为f（σi j）＝C⼜称为屈服函数，式中C是与材料性质有关⽽与应⼒状态⽆关的常数，可通过试验求得。

屈服准则是求解塑性成形问题必要的补充⽅程。

ansys蠕变应变率命令流1.引言1.1 概述概述：蠕变应变是材料在长时间作用下产生的变形现象，它在工程领域具有重要的作用。

蠕变应变率是描述蠕变现象发生速率的参数，它反映了材料在一定应力下产生蠕变变形的能力。

ANSYS是一种常用的工程仿真软件，它提供了许多功能强大的命令流供用户使用。

其中，蠕变应变率命令流被广泛应用于材料蠕变性能的研究和工程实践中。

本文将对ANSYS蠕变应变率命令流进行详细介绍和使用方法的讲解。

通过学习和掌握这一命令流，工程师和研究人员可以更加准确地预测材料在长时间持续加载下的变形情况，为工程设计提供科学依据。

在介绍ANSYS蠕变应变率命令流之前，我们将先简要概述蠕变现象、蠕变应变和蠕变应变率的基本概念。

然后，我们将详细讲解蠕变应变率命令流的使用方法，包括命令的输入格式、参数的设置以及结果的分析等内容。

最后，我们将通过实例的展示和分析，进一步说明蠕变应变率命令流在实际工程中的应用价值。

通过本文的学习，读者将能够全面了解ANSYS蠕变应变率命令流的原理和功能，掌握蠕变应变率命令流的使用方法，并能够灵活应用于工程设计和材料研究中。

同时，本文也将对该命令流存在的一些局限性进行探讨，并对未来的研究方向进行展望。

1.2 文章结构本文主要介绍了ANSYS蠕变应变率命令流的使用方法。

文章共分为引言、正文和结论三个部分。

引言部分首先概述了本文的主题和目的。

其次，介绍了ANSYS蠕变应变率命令流在工程领域的重要性和应用背景。

最后，明确了本文的目的和意义，即通过详细介绍ANSYS蠕变应变率命令流的使用方法，为读者提供一个全面了解和掌握该技术的指南。

正文部分主要包括两个小节，分别是ANSYS蠕变应变率命令流的介绍和使用方法。

- 在2.1小节中，将详细介绍ANSYS蠕变应变率命令流的背景和原理。

首先，解释了蠕变现象的定义和原因。

接着，介绍了应变率是描述蠕变行为的重要参数。

随后，详细阐述了ANSYS蠕变应变率命令流在工程仿真中的作用和应用范围。

蠕变分析教学提纲蠕变分析4.4 蠕变分析4.4.1 蠕变理论4.4.1.1 定义蠕变是率相关材料非线性，即在常荷载作用下，材料连续变形的特性。

相反如果位移固定，反力或应力将随时间而变小，这种特性有时也称为应力松驰，见图4-18a。

图4-18 应力松弛和蠕变蠕变的三个阶段如图4-18b所示。

在初始蠕变阶段，应变率随时间而减小，这个阶段一般发生在一个相当短的时期。

在第二期蠕变阶段，有一个常应变率，所以应变以常速率发展，在第三期蠕变阶段，应变率迅速增加直到材料失效。

由于第三期蠕变阶段所经历的时间很短，材料将失效，所以通常情况下，我们感兴趣的是初始蠕变和第二期蠕变。

ANSYS程序中的蠕变行为用来模拟初始蠕变和第二期蠕变。

蠕变系数可以是应力、应变、温度、时间或其它变量的函数。

在高温应力分析中(如核反应堆等)，蠕变分析非常重要。

例如，假设在核反应堆中施加了预荷载，以保证与相邻部件保持接触而不松开。

在高温下过了一段时间后，预荷载将降低(应力松驰)，可能使接触部件松开。

对于一些材料如预应力砼，蠕变也可能十分重要。

最重要的是要记住，蠕变是永久变形。

4.4.1.2 理论介绍蠕变方程：我们通过一个方程来模拟蠕变行为，此方程描述了在实验中观测到的主要特征（特别是在一维的拉伸实验中）。

这个方程以蠕应变率的方式表示出来，其形式如下：上式中，A、B、C、D是从实验中得到的材料常数，常数本身也可能是应力，应变，时间或温度的函数，这种形式的方程被称为状态方程。

上式中，当常数D为负值时，蠕应变率随时间下降，材料处于初始蠕变阶段，当D为0时，蠕应变率为常值，材料处于第二期蠕变阶段。

对于2－D或3－D应力状态，使用VON Mises方程计算蠕应变率方程中所使用的标量等效应力和等效应变。

对蠕变方程积分时，我们使用经过修改的总应变，其表达式为:经过修改的等效总应变为:其等效应力由下式算出：其中：G=剪切模量＝等效蠕应变增量由程序给出的某一种公式进行计算，一般为正值，如果在数据表中，则使用的是衰减的蠕应变率而不是常蠕变率，但这个选项一般不被推荐，因为在初始蠕变所产生的应力为主的情况下，它可能会严重的低估蠕变值。

第四章材料非线性分析4。

1 材料非线性概述许多与材料有关的参数可以使结构刚度在分析期间改变。

塑性、非线性弹性、超弹性材料、混凝土材料的非线性应力—应变关系，可以使结构刚度在不同载荷水平下（以及在不同温度下）改变。

蠕变、粘塑性和粘弹性可以引起与时间、率、温度和应力相关的非线性。

膨胀可以引起作为温度、时间、中子流水平(或其他类似量)函数的应变。

ANSYS程序应可以考虑多种材料非线性特性：1．率不相关塑性指材料中产生的不可恢复的即时应变。

2．率相关塑性也可称之为粘塑性，材料的塑性应变大小将是加载速度与时间的函数.3．材料的蠕变行为也是率相关的,产生随时间变化的不可恢复应变，但蠕变的时间尺度要比率相关塑性大的多。

4．非线性弹性允许材料的非线性应力应变关系,但应变是可以恢复的。

5．超弹性材料应力应变关系由一个应变能密度势函数定义，用于模拟橡胶、泡沫类材料,变形是可以恢复的。

6．粘弹性是一种率相关的材料特性，这种材料应变中包含了弹性应变和粘性应变。

7．混凝土材料具有模拟断裂和压碎的能力.8．膨胀是指材料在中子流作用下的体积扩大效应。

4。

2 塑性分析4。

2。

1 塑性理论简介许多常用的工程材料，在应力水平低于比例极限时，应力—应变关系为线性的。

超过这一极限后，应力—应变关系变成非线性,但却不一定是非弹性的。

以不可恢复的应变为特征的塑性，则在应力超过屈服点后开始出现.由于屈服极限与比例极限相差很小，ANSYS程序在塑性分析中,假设这二个点相同，见图4—1。

图4-1 弹塑性应力—应变曲线塑性是一种非保守的(不可逆的），与路径相关的现象.换句话说，荷载施加的顺序，以及什么时候发生塑性响应，影响最终求解结果。

如果用户预计在分析中会出现塑性响应,则应把荷载处理成一系列的小增量荷载步或时间步,以使模型尽可能附合荷载-响应路径.最大塑性应变是在输出(Jobname.OUT）文件的子步信息中打印的。

在一个子步中，如果执行了大量的平衡迭代，或得到大于15%的塑性应变增量，则塑性将激活自动时间步选项［AUTOTS ］（GUI ：Main Menu 〉Solution 〉 Sol'n Control ：Basic Tab 或 Main Menu 〉Solution 〉Unabridged Menu> Time /Frequenc 〉Time and Substps)。