当前位置：文档之家 › 地质统计学与变差函数

地质统计学与变差函数

  • 格式：pdf
  • 大小：167.11 KB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

地质统计学.

地质统计学.

2、统计概率
频率：设随机事件A，在次试验中发生m次，其比值m/n称为随机事件A 的频率
显然 当重复试验的次数充分大时，随机事件A的频率（A）常常稳定在 一个确定的数字附近，这就是概率。
概率：在一定的相同条件下，重复作n次试验中发生了m次，当n充分大 时，随机事件A的频率m/n稳定在某一数字P附近，称数值P为该随机事件 的概率。 记为 P(A)=P
3、经典概率统计学所研究的变量原则上都是可以无限次重复试验或大量观 察的，但地质变量则不行。因为一旦在矿体某处取一样品后，严格说来， 就不可能在同一地方再次取到样品了。
4、经典统计学一般要求每次抽取样品必须是独立进行的，但地质变量在两 个相邻样品中的值就不见得一独立的，往往有某种成都的相关性。
地质统计学的优点
4、随机模拟
随机模拟是从一个随机函数(RF)模型中提取多个等 概率的所有随机变量（RV）的联合实现。 在随机模拟中，研究的内容包括随机模拟的定义及 其与插值的区别，随机模拟的基本原理，随机模拟 的分类，典型的随机模拟方法及其计算机实现。
本课程还将介绍地质统计学在储层建模中的应用 包括资料的准备建模的步骤，成果的显示等。
第二章 预备知识
一、概率论基础 二、随机变量及其概率分布 三、随机变量的数字特征 四、统计推断基础
一、概率论基础
1、随机事件 概率论是研究自然界偶然现象的科学，在概率论中把
偶然现象称为随机现象。 在自然界，介于“必然事件”和“偶然事件”之间的
即是“随机事件”。这类事件的特征是在一定条件下可 能发生，也可能不发生，或者在一定条件下有多个可能 发生的结果，而其结果事先不能预测。
3、不但可以进行样品的整体估计，最重要的是可以进行样品的局部估计
4、应用地质统计学方法得到的地质变量的精度比传统方法要精确，可以避 免系统误差。

第四、五讲 地质统计学理论基础

第四、五讲 地质统计学理论基础

当空间一点x固定之后，Z(x)（表示x点处的矿石 品位）就是一个随机变量，体现了其随机性。
在空间两个不同点x及x+h(此处h也是个三维向量
(hu,hv,hw)。它的模
h
h h h 2 2 2
u
v
w
表示x点与(x+h)点
的距离）处的品位Z(x)与Z(x+h)具有某种程度的
相关性，这就体现了其结构性的一面。
6/88
区域化变量的属性
• 1、空间局限性 • 2、连续性 • 3、异向性 • 4、相关性 • 5、叠加性
7/88
1、空间局限性
区域化变量被限制 于一定的空间，该 区间称为区域化变 量的几何域。例如， 矿体的范围，油藏 的范围，断块的范 围等都可以看成是 区域化变量的几何 域。
Z(xi)
Z(xk) Z(xj)
第三章 区域化变量与变差函数
区域化变量及其基本特征 变差函数的定义 变差函数曲线 变差函数的理论模型 变差函数的结构分析
1/88
第一节 区域化变量
区域化变量（Regionalized Variable) 是地质统计学研究的对象,它是一种在空
间上具有数值的实函数(G Matheron),也就 是说,它在空间的每一个点取一个确定的数 值,即当由一个点移到下一个点时,函数值 是变化的
2 (x, h) Var[Z(x) Z(x h)]
E[Z (x) Z (x h)]2 {E[Z (x)] E[Z(x h)]}2
Z(x1)
观测前是一个随机场，
Z(x2)Z(x7) NhomakorabeaZ(x3) Z(x6) Z(x8)
依赖于坐标（xu,xv,xw)
Z(x4) Z(x5)

地质统计学中变差函数参数估计的新方法

地质统计学中变差函数参数估计的新方法

本文1997年11月收到,张启芳编辑。

3本研究得到“九五”攻关课题(95-B02-02-02)资助。

地质统计学中变差函数参数估计的新方法3 黄诗峰 金菊良 段进军 文玉明(中国科学院地理研究所・北京・100101)　(河海大学・南京・210098)　(中国科学院地理研究所・北京・100101) 遗传算法是一种模拟生物进化规律的全局优化算法。

对传统的遗传算法进行改进,并应用于地质统计学变差函数参数估计中。

实例分析表明,该方法简便、通用,具有较高拟合精度,是非线性、不连续可微模型参数估计的方法。

关键词　地质统计学　变差函数　遗传算法　参数估计 地质统计学已广泛应用于空间分布数据的空间结构性和随机性分析及其最优线性无偏内插估计之中,在地质、地球化学领域得到大力推广[1],现也引起地球信息科学研究者的注意[2,3]。

变差函数(Var 2iogram )是地质统计学基本工具,其定义为:r (h )=12E [z (χ)-z (χ,h )]2(1) 式中,h 为距离滞后,或称步长,E 表示数学期望,z (x )为在位置x 处的变量值,z (x ,h )为在位置x 偏离h 处的变量值。

由于采样点往往是离散的,上式被改写为:r (h )=12N (h )∑N (h )i =1[z (χi )-z (χi +h )]2　(2)称为实验变差函数,式中,N (h )是距离等于h 的点对数,z (x i )为处于点x i 处变量实测值,z (x i +h )为与点x i 偏离h 处变量的实测值。

随着步长h 的变化可计算出一系列的变差函数值。

以h 为横坐标,r (h )为纵坐标作图,得到实验变差函数曲线。

变差函数理论模型有球状模型、指数模型、高斯模型、幂函数模型、对数函数模型、纯块金效应和空穴效应模型等。

其中球状模型应用最为广泛,大多数情况下可用球状模型进行拟合。

对于变异性很大的空间变量,其变差函数还常需采用多个模型进行套合模拟,如二级套合球状模型。

地质统计学(5)_变差函数及结构分析cjg2011

地质统计学(5)_变差函数及结构分析cjg2011

证：性质④
Ck’k(-h) =E[Zk’(x-h)Zk(x)]-mk’mk 令：y=x-h, 则x=y+h 代入上式得： Ck’k(-h) =E[Zk(y+h)Zk’(y)]-mk’mk= Ckk’(h) 因E[Zk(y+h)Zk’(y)]不一定等于E[Zk’(y+h)Zk(y)] ，故Ckk’(h)不一定等于 Ck’k(h) ，即交叉协方差函数Ckk’(h)对h和（-h）无对称性，这是较特殊的情 况。 因此，在两个变量出现迟后效应时，应采用交叉协方差函数进行研究。
证：性质⑤
2 k k (h ) = zk (x + h ) - z k (x )zk (x + h ) - zk (x )
= zk (x + h ) - mk - z k (x ) - mk zk (x + h ) - mk - z k (x ) - mk = zk (x + h ) - mk z k (x + h ) - mk - z k (x + h ) - mk z k (x ) - mk = zk (x + h )z k (x + h ) - mk mk - z k (x + h )z k ( x ) - mk mk = Ck k (0) - Ck k (h ) - Ckk (h ) + Ckk (0) = 2Ck k (0) - Ck k (h ) + Ckk (0) - zk ( x + h )z k (x ) - mk mk + z k (x )zk (x ) - mk mk - z k (x ) - mk z k (x + h ) - mk + z k (x + h ) - mk z k (x ) - mk

地质统计学原理

地质统计学原理

地质统计学原理
1 变差函数（Variogram）基础
变差函数是用来描述油藏属性空间变化的一种方法，可以定量的描述区域化变量的空间相关项。

变差函数的原理是空间上相近的样品之间的相关性强，而相距较远的样品之间的相关性较小，当超过一个最小相关性时，距离的影响就不大了。

这种空间上的相关性是各向异性的，因此需要从不同方向上描述某个属性的变差函数。

通过从输入数据中得到变差函数，在属性模型中利用变差函数建模，从而可以在最终模型中体现出实验数据的空间相关性。

1.1 变差函数原理与数据分析
1.1.1 变差函数的原理
变差函数图即变差函数与滞后距（空间的距离）的关系图。

计算方法是：对一组滞后距相近的数据，计算这组数据的变差，最后做出不同滞后距的变差曲线。

Sample variogram
从一组实验样本数据中计算结果。

Variogram model
根据理论变差函数模型拟合的结果。

Transition
曲线类型。

常用的变差函数类型有指数型、球状模型、高斯模型。

Plateau
在变差函数曲线上，随着横坐标距离的增加，纵坐标变差值不再增加，即为Plateau。

Range
变程：当曲线达到高台水平段（Plateau）时的距离。

变程范围之内，数据具有相关性，变程范围之外，数据之间互不相关，即变程之外的观测值不对估计结果产生影响。

1。

变差函数的概念与计算分析

变差函数的概念与计算分析

变差函数的概念与计算谷跃民编写在地质统计学随机模拟工作中，统计归纳区域变量的分布和变差函数，是用好随机模拟技术最关键的两项工作，其中区域变量分布统计比较容易理解，变差函数计算过程相对复杂，影响了解释人员对它的直观理解，为了使解释生产人员快速了解变差函数，准确使用相关工具软件，并能依据现有的资料和对工区地质情况的先验信息，统计归纳出合乎实际的变差函数，作者在学习相关知识的基础上，对学习材料进行了初步总结，试图用通俗的方式，对变差函数的概念和统计归纳方法与大家共同进行探讨。

一、变差函数的基本概念在地质统计学中，变差函数是最基本与最重要的模拟工具，它用于描述数据值的空间互相关，数据点在空间上相距越远，相关性就变得越小，变差函数就是模拟这种现象的数学函数，通常用一张图来展示，用X轴表示滞后距离，用Y轴表示方差，可以从区域变量抽取的样本值中计算归纳出来，见图1，它通过变程来反映变量的影响范围，V(h)为变差函数值，Lag(h)为滞后距。

变差函数可以用四个参数来描述：1、变差函数类型：决定了随着滞图1 变差函数图示后距的增加变差（方差）变化的快慢，在JASON STATMOD MC中，使用GAUSSIAN和EXPONENTIAL曲线类型；2、变程a：指的是在超过这个距离后，数据点之间就不再有明显的相关性，也称作影响距离；3、块金效应C0：表示在距离为0时的方差值，用来表示相距很近的两点的样品变化情况；4、先验方差：Sill=C+C0也叫基台值，它反映变量的变化幅度。

二、变差函数的估算与拟合1、变差函数的计算公式与估算变差函数的定义是：区域化变量Z(x)和Z(x+h)两点之差的方差之半，定义为Z(x)的变差函数，数学定义如下：h为滞后距。

如果有了区域化变量Z(x)的一部分采样，就可以估算该区域化变量的Z(x)变差函数，具体计算公式如下：i为样本序号。

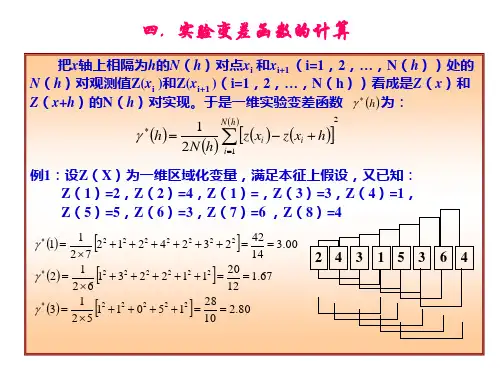
2、变差函数的估算示例为了能更直观、更深刻地体会它的具体意义，下面举两个计算实例，各具体计算两个变差函数值，通过具体计算过程，就会知道什么样的资料可以满足变差函数估算的要求，具体在资料条件会出现怎样的异常，这两个实例分别为两种区域变量类型，一个是垂向区域变量类型，可以理解为井曲线等，一个是平面区域变量类型，可以理解为孔隙度平面变化等。

地质统计学与随机建模原理2-变差函数

地质统计学与随机建模原理2-变差函数


m
m
,不存在
但：zx zx h y y 0 0 ，存在且为0
1） 二阶平稳假设的第二个条件可以推出本征假设条件之二 在二阶平稳假设满足时：
2 h zx zx h zx
2
由二阶平稳假设条件之二 Varz x =C（0），x ，当h=o
2Hale Waihona Puke D2 Z x 或 varZ x
2
D2 Z x VarZ x EZ x EZ x
2
2. 变差函数与变差图
假设空间点x只在一维的x轴上变化，我们把区域化变量Z（x）在x ，x+h两点处的值之差的方差之半定义为Z（x）在x 轴方向上的变差函数 ，记为r (x,h),即:
第二章 地质统计学理论基础
第一节 区域化变量的理论
一、随机场与区域化变量
1．定义：以空间点x的三个直角坐标xu, x v, xw为自变量的随机场
Z(xu,xv,xw）=Z(x）称为一个区域化变量。
[区域化变量具有两重性]：
观测前，将Z(x）看作随机场；观测后，将Z(x）看作一个普通的三元
实值函数。即空间点函数，一次观测后，就得到它的一个实现Z(x)。
二阶矩且平稳就够了。→ 二阶平稳（弱平稳）。
② 二阶平稳假设
满足下列两个条件 1）整个研究区内，Z（x）的数学期望存在，且等于常 数，
zx m(常数），x
2）整个研究区内，Z（x）的协方差函数存在且平稳（ 即只依赖于滞后h，而与x无关）
Covzx , zx h zx zx h zx zx h zx zx h m2 ch, x, h
如一维随机游走：
1 xi 1 Z n xi

地质统计学(3)_实验变差函数的计算cjg2011

地质统计学(3)_实验变差函数的计算cjg2011

1 2 v
2
1 C y t dydt 2 v v
2 —
C y tdydt
v
— —
2 v2
C y ydydy
v
C (V ,V ) C (v, v) 2 C (V , v)
以变差函数*表示为：
— — — C (0) （V ,V ) C (0) （v, v) 2C (0) （V , v) 2
n
Z v m cv, v
2



2
n 1 n 1 x z x i m z j m n j 1 n i 1
x z

1 n i 1 1 n n i 1
Cov xi , z x j z j 1 C xi x j cv, v j 1
n

1 n 1 Cov[ z y , z xi ]dy n i 1 v 1 n 1 Cov y xi dy cv, v n i 1 v
2 （V , v) (V ,V ) （v, v)
2 E
—
—
—
若v是n 个中心点 xi’ (i=1,2,…,n)的钻孔岩心的点集，则：
1 n z z xi n i 1

n
上述 公式仍然成立。
2
1 事实上： ( z ) z xi m ，而 E(Zv)=m
2 i V , xi V ,V i j xi x j

2010_03变差函数

2010_03变差函数
地质统计学 Geostatistics
Review of main points

地质统计学的发展、主要贡献者、主流软件 储层地质建模的意义和必要性 地质统计学能与不能 两个重要概念：

uncertainty， spatial correlation
Review of main points 回顾了概率论的一些基本的概念
110
110
105
105
105
100
100
100
95
95
95
90 90 95 100 105 1st of Pair 110 115 120
90 90 95 100 105 1st of Pair 110 115 120
90 90 95 100 105 1st of Pair 110 115 120
Tail
Head
Head
Combining Variogram Points


Each h-scatterplot is summarized by an average squared difference and the values are plotted together The h-scatterplots may be useful to view in presence of very few data

100
Semivariance
95
Graph summary statistic against h for many lags
90 90 95 100 105 1st of Pair 110 115 120
Variogram Calculation Pair Combinations h=200m

03变差函数

03变差函数

1 r ( x, h ) = Var [z ( x ) − z ( x + h )] 2 1 1 2 2 = Ε[z ( x ) − z ( x + h )] − {Ε[z ( x )] − Ε[z ( x + h )]} 2 2
1 2 (xi − x j ) γ (h ) = ∑ 2 N (h ) (i , j ) hi , j ≈ h
Spatial Continuity
variance or covariance


Correlation and hence covariance decrease as h (the separation) increases : measure of similarity Semivariance increases as h increases : dissimilarity
30
Total Variance
25
Semivariance
20 15
10 5 0 0 100 200
300 400 500 600
Lag (m)
Plot as a Function of Distance

Variogram function:
Each point corresponds to an h-scatterplot
Variogram Calculation (Difference)2 for h=100m
16 0 4 9
115
109
811054105103106
103
0 4
97
25
106
25
104
64 9
109
103
49

03地质统计学与变异函数

03地质统计学与变异函数




西南石油学院Βιβλιοθήκη 教务处地质统计学与变差函数

区域化变量

由于区域化变量具有上述特殊性质，经典概率统计方法不 能处理这类问题，而地质统计学中的一个基本工具——变 差函数（或叫变异函数、变程方差函数），就能较好地研 究区域化变量的特殊性质
从概率知道，要完整地描述一个随机变量的特征，必须给出它的 分布函数或分布密度，对于区域化变量也是一样。对于区域化变 量，最为重要的是它的平均值、方差和相关函数。它们都是由随 机变量的数字特征引伸出来的，二者很类似。不过随机变量的数 字特征是数值，而区域化变量的数字特征一般都是函数。因为， 从本质上看，区域化变量是一个随机函数，不是一个随机变量
西南石油学院
教务处
地质统计学与变差函数

地质统计学的诞生

G. 马特隆指出： “ 从历史的角度来看，地质统计学和采矿业 是同时出现的。就反映矿化空间特征而论，那些传统的方法 仍保持着它们的全部价值，现代的理论成就决不是要否定这 些方法，而是把它们当作出发点，并将其提到更高的科学水 平。 ” 地质统计学的诞生为在地质勘探和采矿工程中应用新 的统计学方法开拓了前景
西南石油学院 教务处


地质统计学与变差函数

地质统计学的现状及优点

优点
地质统计学之所以能得到迅速发展和广泛应用，是因为它与传统 的方法和经典概率统计方法在地质采矿的应用相比有一系列明显 的优点

地质统计学并不是将经典统计方法简单地用于地质、采矿领域， 而是从地质、采矿的实际出发，对原有的数学理论与方法加以选 择、创新，使之更有效地解决地质、采矿中的问题 它最大限度地利用勘探工程所提供的各种信息。在使用克立格法 估计矿床中某一块段变量的平均值时，充分考虑了待估块段与信 息样品之间的空间位置关系、信息样品彼此之间的空间位置关系 以及区域化变量空间分布的结构特征等方面的因素

地质统计学(1)_概 述

地质统计学(1)_概 述

第二节 地质统计学的研究现状及优点
一、研究现状
理论上的两大学派： • 以G. 马特隆为首的“枫丹白露地质统计学派”
– 以正态假设为基础的析取克立格法及条件模拟的研究，同时把主成分 分析和协同克立格法结合起来，提出多元地质统计学的基本思想，形 成了简单克立格、普通克立格、泛克立格以及析取克立格等一套理论 和方法
60
80
100
距离
这个例子直观地说明了经典统计不能反映矿化强度的空间变化性这一弱点。）
缺陷2：要求变量为纯随机变量，且服从 一定的已知概率分布，而地质变量明显地 既具有随机性，又具有结构性。
缺陷3：所研究的变量原则上可无限次重 复实验或大量观测。而地质变量不可能达 到，样品一但取出，不可能在同一处再获 得。
泛克里格法和K阶本征函数法等
（3）条件模拟
对矿床的条件模拟和对采矿过程的条件模拟
（4）平稳非线性地质统计学
条件数学期望、析取克里格法等
（5）非参数地质统计学
指示克立格法等
以平均品位考察问题的缺陷
问题1：样品的代表性问题：“承载、支撑、支架、支集”即钻孔 取心样品承载小，而块段承载大。两者不可能等同的结果是：低品位估 计过低，高品位估计过高。
问题2：品位空间变化问题：矿化的空间结构。如：走向上变化小 ，倾向变化大，权值不一样。
问题3：矿化强度的空间变化问题：离散度。这与问题2相关联，离 散度是衡量经济开采可行度的重要因素。
G 2
(0.50%)
d2 (60m)
G 7 (1.00%)
d7 (75m)
d6 (60m ) d9 (45m)
G 9
(0.70%) (0.60%)
G 3
G 6
(0.50%)

【免费下载】变差函数的概念与计算分析

【免费下载】变差函数的概念与计算分析

变差函数的概念与计算谷跃民编写在地质统计学随机模拟工作中，统计归纳区域变量的分布和变差函数，是用好随机模拟技术最关键的两项工作，其中区域变量分布统计比较容易理解，变差函数计算过程相对复杂，影响了解释人员对它的直观理解，为了使解释生产人员快速了解变差函数，准确使用相关工具软件，并能依据现有的资料和对工区地质情况的先验信息，统计归纳出合乎实际的变差函数，作者在学习相关知识的基础上，对学习材料进行了初步总结，试图用通俗的方式，对变差函数的概念和统计归纳方法与大家共同进行探讨。

一、变差函数的基本概念在地质统计学中，变差函数是最基本与最重要的模拟工具，它用于描述数据值的空间互相关，数据点在空间上相距越远，相关性就变得越小，变差函数就是模拟这种现象的数学函数，通常用一张图来展示，用X轴表示滞后距离，用Y轴表示方差，可以从区域变量抽取的样本值中计算归纳出来，见图1，它通过变程来反映变量的影响范围，V(h)为变差函数值，Lag(h)为滞后距。

变差函数可以用四个参数来描述：1、变差函数类型：决定了随着滞图1 变差函数图示后距的增加变差（方差）变化的快慢，在JASON STATMOD MC中，使用GAUSSIAN和EXPONENTIAL曲线类型；2、变程a：指的是在超过这个距离后，数据点之间就不再有明显的相关性，也称作影响距离；3、块金效应C0：表示在距离为0时的方差值，用来表示相距很近的两点的样品变化情况；4、先验方差：Sill=C+C0也叫基台值，它反映变量的变化幅度。

二、变差函数的估算与拟合1、变差函数的计算公式与估算变差函数的定义是：区域化变量Z(x)和Z(x+h)两点之差的方差之半，定义为Z(x)的变差函数，数学定义如下：h为滞后距。

如果有了区域化变量Z(x)的一部分采样，就可以估算该区域化变量的Z(x)变差函数，具体计算公式如下：i为样本序号。

2、变差函数的估算示例为了能更直观、更深刻地体会它的具体意义，下面举两个计算实例，各具体计算两个变差函数值，通过具体计算过程，就会知道什么样的资料可以满足变差函数估算的要求，具体在资料条件会出现怎样的异常，这两个实例分别为两种区域变量类型，一个是垂向区域变量类型，可以理解为井曲线等，一个是平面区域变量类型，可以理解为孔隙度平面变化等。

地质统计学反演中的变差函数简介及模型分类

地质统计学反演中的变差函数简介及模型分类

地质统计学反演中的变差函数简介及模型分类在地质统计学反演工作中，变差函数是一个重要的控制参数。

它是区域化变量空间变异性的一种度量，反映了空间变异程度随距离而变化的特征。

平时工作中，部分地球物理技术人员对该参数不易理解，本次就向大家简要介绍一下。

从直观上看，变差函数图展示的是方差与距离的交汇图。

观察下面三条曲线，如果你为这些不同的数据集制作变差函数，看起来将是什么样子呢？下图就是输出的变差函数图。

下图是一个典型变差函数图像，有一些重要参数控制。

重要参数变程(range)：指区域化变量在空间上具有相关性的范围。

在变程范围内，数据具有相关性，而在变程之外，数据之间互不相关，即在变程以外的观测值不对估计结果产生影响。

块金值(nugget)：变差函数如果在原点间断，这在地质统计学中被称为“块金效应”，表现为在很短的距离内有较大的空间变异性。

需要注意的是，它可以由地质的变异性造成，也可能是由于测量误差造成。

拱高：在取得的有效数据尺度上，可观测得到的变异性幅度大小。

基台值(sill)：基台值为变量在空间上总变异性的大小，即为变差函数在H大于变程的值，即块金值和拱高之和。

滞后距滞后是地质统计学术语，定义为沿关注的方向上网格节点的距离。

垂向滞后距：滞后距劈分的距离h通常与数据的采样间隔一致。

测井孔隙度曲线通常以0.5英尺为一个采样间隔，因此滞后距应该设置为0.5或者0.5的整数倍。

水平滞后距应该沿网格节点方向设置。

变程方向变程方向方向包含两个概念：垂向变程方向和水平变程方向众所周知，由于在大多数的项目研究中，井的不规则零散分布使我们很难得到一个很好的水平变差函数。

因此在EarthmodelFT软件中，没有提供水平方向变差函数的分析工具。

而在Jason软件中，通过对提取的面属性并结合地质认识分析，来得到水平方向的变差函数。

变差函数模型的分类在地质统计学研究过程中，需要进行数据的空间结构分析，拟合变差函数。

在实验变差函数图中，数据点相对较离散，因此需要拟合出一条最优的理论变差函数曲线。

地质统计学

地质统计学
下了较广泛的定义： “地质统计学就是随机函数的形式体系在勘探和 估计自然现象的应用” 。现在一般认为“地质统计学是以变差函数为基本工具，在研究区域 化变量的空间分布结构特征规律性的基础上， 综合考虑空间变量的随机性和结构性的一种数 学方法” 。地质统计学之所以得到迅速发展，是因为它又自身的明显的优点，主要表现在： （1）地质统计学从地质研究的实际出发，对原有的数学理论和方法加以选择和创新，使之 更有效的解决地质问题。 （2）能够最大限度的利用已知信息，充分考虑了未知地区与已知信息的空间关系及区域化 变量的结构特征。 （3）不仅可以进行整体估计，还可以进行局部估计。 （4）估计精度高，并能具体给出估计精度的概念，克立格方差是一个很好的度量估计精度 的概念。 （5）地质统计学方法与计算机相结合，并自动成图和拼图，从而省时和省力。 （6）随机模拟可以很好的再现地质变量的变化，从而为定量研究地质体提供了可靠保障和 有利基础。
一个随机函数。 简单地说依赖于参数的随机变量叫做随机函数。 当随机函数依赖多个自变量时，称为随机场。 2、 随机过程： 通常把只依赖于时间参数 t ( xi = t ) 的随机函数， 称作随机过程。 记为 Z (t , ω ) ， 简称 Z (t ) 。 当每次试验取得一个结果时， 随机过程变为一般的 t 的实值函数 f (t ) = Z (t , ω ) 。 当参数 t 取固定值时，随机过程变为一纯随机变量 Z (ω ) = Z (t 0 , ω ) 。当然随机过程中的参 数 t 也可以不是时间，而是其它含义，如深度等。 3、区域化变量 （Regionalized Variagram） G.马特隆将区域化变量定义为：一种在空间上具有数值的实函数，它在空间的每一个点 取一个确定的值，当由一个点移到另一个点时，函数值是变化的。 现在一般认为，区域化变量是指以空间点 X 的三个直角坐标 ( xu , xv , x w ) 为自变量的随 机场 Z ( x u , x v , x w ) = Z ( x) 。 区域化变量具有两重性： 观测前把它看成是随机场， 而观测后把它看成一个空间点函数。 区域化变量可以同时反映地质变量的结构性和随机性。当空间点 X 固定后，地质变量的 取值是不确定的， 可以看作一个随机变量， 体现在随机性； 另一方面， 空间两个不同点之间， 地质变量又具有某种自相关性，且一般而言，两点距离越小，相关性越好，反映了地质变量 的连续性和关联性，体现了结构性一面。正因为区域化变量具有这种特性，才使得地质统计 学具有强大生命力。 从地质学的观点来看，区域化变量可以反映地质变量的以下特征： ① 局部性：区域化变量只限于一定的范围内。这一范围称为区域化的几何域。区域化变 量一般按几何承载定义的，承载变了就会得到不同的区域化变量。 ② 连续性：不同的区域化变量具不同的连续性，可用变差函数描述。 ③ 导向性：当区域化变量在个方向上相同时，称各向同性，否则称各向异性。 ④ 可迁性：区域化变量在一定范围内具一定程度的空间相关性。当超出这个范围时，相 关性很弱甚至消失。这种性质用一般统计方法很难识别。 ⑤ 对任一区域化变量而言，特殊的变异性可迭加在一般规律之上。 上述这些特征， 经典概率统计方法很难处理， 而地质统计学中的基本工具——变差函数， 能较好地研究这些特殊性质。

Petrel建模中的几点认识

Petrel建模中的几点认识

Petrel建模中的几点认识引言20世纪初年代发展起来的以井资料为主的三维地质建模技术，目前已成为油田开发阶段油藏研究的重要手段之一。

Schlumberger公司的Petrel虽然在地震解释方面有不错的表现，但己经不再是仅仅定位在建模上的勘探开发一体化工具，建模仍然是它的突出特点。

在完成构造建模的基础上，分2个阶段进行建模:①采用针对离散变量(如岩相)的模拟方法，建立储层骨架模型;②在储层骨架边界的控制下，对储层连续性变量的模拟方法建立储层参数模型，相建模是2个阶段建模的关键。

笔者旨在探讨Petrel软件中进行相建模和变差函数求取中的几点认识。

1.相模型的建立相分布控制着砂体分布，只有砂体内才具有有效的储层参数，不同相的储层参数分布规律不同，相控建模过程充分体现了地质思维和地质知识，更增加了地质因素对于属性模型的控制。

尤其是对于成岩与后生改造作用不强的储层，原始沉积作用控制着储层宏观非均质性，沉积相带的交替是制约储层性质的根本因素叫，当没有相约束时，各个储层参数建模之间的差别相当大，用沉积相或者岩相约束进行相控建模成为必然选择。

相控建模时可采用沉积相约束和岩相约束2种方法，Petrel在相建模和属性建模中采用了GSLIB中成熟的技术和方法。

随机模拟的方法很多，目前应用最多、最成功的方法是序贯模拟方法，至于模拟相模型时采用哪种计算方法，这里不再赘述。

尽管Petrel提供了多达7种建立相模型的方法，笔者仅就实际操作过程中常用的3种进行讨论。

1.1手工勾绘沉积相图使用手工勾绘的沉积相图作为约束条件时，PeIrel中的相控建模，就变成了相带图的立体化，模拟出的孔、渗边界就是生硬的沉积相边界。

相的引入是作为参数模拟的边界条件，在不同相的内部实现参数模拟，笔者认为这种做法使Petrel的功能削弱了，可见，手工勾绘沉积相图只适于对随机模拟的相模型进行局部修改。

1.2采用岩相模型代替沉积相模型当没有足够细致的沉积微相研究时，模拟的沉积相模型的精细程度将有所欠缺，进而导致井间单砂体的连通性、砂体的尖灭及砂体内部的泥岩夹层等得不到很好的反映;相反，当用泥质含量曲线划分岩相时，模型的纵向分辨率可以直接和0.125m采样率的电测曲线进行对比，单砂体的连通性、砂体的尖灭等都得到很好的反映。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Geostatistical methods are optimal when data are - normally distributed and - stationary (mean and variance do not vary significantly in space) Significant deviations from normality and stationarity can cause problems, so it is always best to begin by looking at a histogram or similar plot to check for normality and a posting of the data values in space to check for significant trends. The posting above shows some hint of a SW-NE trend, which we will check later.
4
Exploratory Analysis of Example Data Our example data consist of vertically averaged porosity values, in percent, in Zone A of the Big Bean Field (fictitious, but based on data from a real field). Porosity values are available from 85 wells distributed throughout the field, which is approximately 20 km in east-west extent and 16 km north-south. The porosities range from 12% to 17%. Here are the data values posted at the well locations:
6
Spatial Covariance, Correlation and Semivariance You have already learned that covariance and correlation are measures of the similarity between two different variables. To extend these to measures of spatial similarity, consider a scatterplot where the data pairs represent measurements of the same variable made some distance apart from each other. The separation distance is usually referred to as “lag”, as used in time series analysis. We’ll refer to the values plotted on the vertical axis as the lagged variable, although the decision as to which axis represents the lagged values is somewhat arbitrary. Here is a scatterplot of porosity values at wells separated by a nominal lag of 1000 m:
C.V. Deutsch, 2002, Geostatistical Reservoir Modeling, Oxford University Press, 376 pages. o Focuses specifically on modeling of facies, porosity, and permeability for reservoir simulation. C.V. Deutsch and A.G. Journel, 1998, GSLIB: Geostatistical Software Library and User's Guide, Second Edition, Oxford University Press, 369 pages. o Owner's manual for the GSLIB software library; serves as a standard reference for concepts and terminology. P. Goovaerts, 1997, Geostatistics for Natural Resources Evaluation, Oxford University Press, 483 pages. o A nice introduction with examples focused on an environmental chemistry dataset; includes more advanced topics like factorial kriging. E.H. Isaaks and R.M. Srivastava, 1989, An Introduction to Applied Geostatistics, Oxford University Press, 561 pages. o Probably the best introductory geostatistics textbook; intuitive development of concepts from first principles with clear examples at every step. P.K. Kitanidis, 1997, Introduction to Geostatistics: Applications in Hydrogeology, Cambridge University Press, 249 pages. o A somewhat different take, with a focus on generalized covariance functions; includes discussion of geostatistical inversion of (groundwater) flow models. M. Kelkar and G. Perez, 2002, Applied Geostatistics for Reservoir Characterization, Society of Petroleum Engineers Inc., 264 pages. o Covers much the same territory as Deutsch's 2002 book; jam-packed with figures illustrating concepts. R.A. Olea, 1999, Geostatistics for Engineers and Earth Scientists, Kluwer Academic Publishers, 303 pages. o Step by step mathematical development of key concepts, with clearly documented numerical examples.
Some spatially autocorrelated parameters of interest to reservoir engineers: facies, reservoir thickness, porosity, permeability
2
Some Geostatistics Textbooks
5
Looking at the histogram (with a normal density superimposed) and a normal quantile-quantile plot shows that the porosity distribution does not deviate too severely from normality:
Links to some software and online resources are available at /~gbohling/geostats
3
Basic Components of Geostatistics (Semi)variogram analysis – characterization of spatial correlation Kriging – optimal interpolation; generates best linear unbiased estimate at each location; employs semivariogram model Stochastic simulation – generation of multiple equiprobable images of the variable; also employs semivariogram model
INTRODUCTION TO GEOSTATISTICS And VARIOGRAM ANALYSIS
C&PE 940, 17 October 2005
Geoff Bohling Assistant Scientist Kansas Geological Survey geoff@ 864-2093
Geostatistical routines are implemented in the major reservoir modeling packages like Petrel and Roxar’s Irap RMS; used in the generation of grids of facies, permeability, porosity, etc. for the reservoir.