喇叭天线的设计1206030201

手把手教你制作喇叭天线
1 喇叭天线简介
 喇叭天线简介常见的喇叭天线主要由角锥喇叭（矩形喇叭）和圆锥喇叭，分别如图1.1、1.2 所示：
 图1.1 角锥喇叭实物图
 图1.2 圆锥喇叭实物图
 从阻抗匹配的角度来理解，天线其实就是一个阻抗转换器，从传输线到自由空间（377 欧姆），一个通用的微波传输线就是波导（waveguide）一个空的引导电磁波传输的矩形管（hollowpipe），如果波导横截面的口径大于半个波长，那幺电磁波就能在其中以较低的损耗传输，并且如果波导终端打开，那幺电磁波就可以向自由空间辐射。

 喇叭就是一个渐变的波导，它增大了辐射口径，可以获得较高的增益，而且制作简单，性能稳定，即便在较恶劣的环境中也能获得较好的方向图，下面我们就自己动手设计一个角锥喇叭天线，设计中将要用到两个软件：
HDL_ANT 和CST（或HFSS），分别用于设计和仿真。

天线原理与设计—第六章口径天线和喇叭天线口径天线是一种特殊的天线，其工作原理是通过改变天线口径的大小以实现方向性辐射。

喇叭天线则是一种具有喇叭形状的天线，其主要功能是对电磁波进行聚焦或分散，从而实现天线的增益和波束的调控。

本章将介绍这两种天线的基本原理和设计方法。

6.1口径天线6.1.1口径天线的基本原理口径天线的基本原理是利用天线口径的大小来控制电磁波的发射和接收方向。

根据狄拉克定理，天线辐射的功率密度与天线口径的平方成正比。

因此，通过改变天线口径的大小，可以调整天线的辐射功率和波束的方向性。

一般情况下，口径天线的口径越大，辐射功率越大，波束的方向性越好。

6.1.2口径天线的设计方法口径天线的设计方法主要包括天线口径的确定和辐射模式的设计。

天线口径的确定需要考虑到工作频率、辐射功率和波束方向等参数。

一般情况下，口径天线的口径选取为波长的几倍，以保证天线的辐射效果和方向性。

辐射模式的设计则需要根据具体的应用要求，确定天线的辐射方式和波束的形状。

6.2喇叭天线6.2.1喇叭天线的基本原理喇叭天线是一种特殊形状的天线，其主要功能是将电磁波进行聚焦或分散，从而实现天线的增益和波束的调控。

喇叭天线的基本原理是利用喇叭形状的反射面将电磁波进行反射和聚集。

喇叭天线可以分为抛物面喇叭天线和双曲面喇叭天线。

抛物面喇叭天线主要用于聚焦电磁波，而双曲面喇叭天线主要用于分散电磁波。

6.2.2喇叭天线的设计方法喇叭天线的设计方法主要包括反射面的确定和波束的调控。

反射面的确定需要考虑到工作频率、波束宽度和聚焦距离等参数。

一般情况下，抛物面喇叭天线的反射面采用抛物线形状，双曲面喇叭天线的反射面采用双曲线形状。

波束的调控则需要通过反射面的形状和尺寸来实现，一般情况下，反射面的大小越大，波束的调控能力越好。

综上所述，口径天线和喇叭天线是一种特殊的天线，其工作原理是通过改变天线口径的大小和喇叭形状来实现方向性辐射和波束的调控。

口径天线通过改变天线口径的大小来控制电磁波的发射和接收方向，而喇叭天线则通过喇叭形状的反射面将电磁波进行聚焦或分散。

矩形口径喇叭天线设计
姓名：王亚勇
班级：通信0903
学号：U200913841
2012/5/14
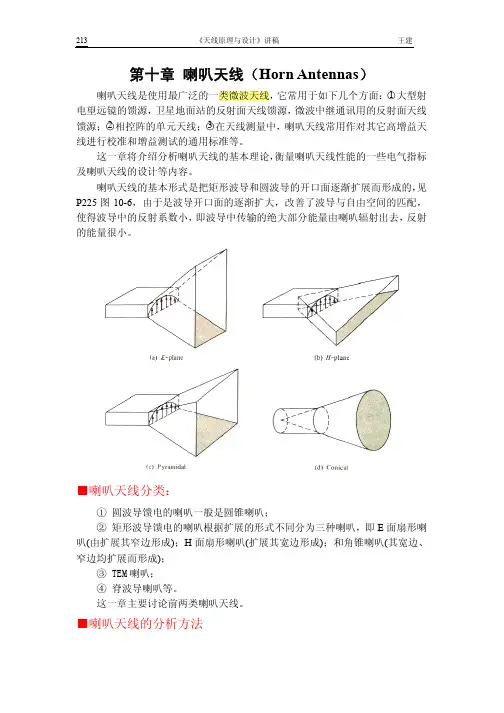
喇叭天线是一种广泛使用的微波天线，其优点是结构简单，频带宽，功率容量大，调整与使用方便，合理的选择喇叭尺寸可以获得良好的辐射特性，相当尖锐的主瓣和较高的增益。

因次，喇叭天线应用非常广泛，它是一种常见的天线增益测试用标准天线。

下面我们用HFSS来设计喇叭天线并对其相关特性和参数进行仿真。

一．实验目的
1.通过实验熟悉使用HFSS.
2.设计一个S频段最佳增益矩形喇叭天线，理解矩形天线的原理，
理解天线各种参数。

二．实验内容
1.打开并运行HFSS后，设置求解类型
2.创建喇叭模型，分别在z=0和z=plength平面上创建大小为
a*b和a1*b1的平面
3.创建WR430波导模型
4.创建同轴馈线（1）同轴线的外导体
（2）同轴线的内导体
5.布尔操作
6.设置天线表面的外表面为理想导体的边界条件
7.设置辐射边界条件
三．求解设置
四．实验结果分析
（1）定义辐射表面
（2）查看E面和H面的增益方向图
（3）查看三维方向下的增益方向图
（4）查看回波损耗S11扫频结果
分析结果看当 2.4Ghz时，S11为-15.356dB，天线的最大增益是20.2143dB，与设计要求的19dB接近，可见设计成功。

五，保存结果
至此，我们完成了矩形口径喇叭天线的设计分析，设计的喇叭天线的最大增益约为20db，与设计要求的19db 接近，最后，单击保存按钮，在选择主菜单上的EXIT命令，退出HFSS。

微波技能与天线课程安排——之阳早格格创做角锥喇叭天线姓名：吴爽教号：1206030201目录一．角锥喇叭天线前提知识34. 最好角锥喇叭近场 E里战 H里的主瓣宽度7二．角锥喇叭安排真例7一．角锥喇叭天线前提知识角锥喇叭是对付馈电的矩形波导正在宽边战窄边均按一定弛角弛启而产生的，如下图所示.矩形波导尺寸为a×b，喇叭心径尺寸为D H×D E，其E里(yz 里)真顶面到心径中面的距离为R ，H 里(xz 里)内真顶面到心径中面的距离为R E,H 里(xz 里)内真顶面到心径中面的距离为R H.1. 心径场角锥喇叭内的电磁场，暂时还已有庄重的剖析解截止，本果正在于，角锥喇叭正在 x战 y二个目标随喇叭的少度目标均是渐变而渐渐扩展的，果而要正在一个正接坐标系下供得角锥喇叭内的场的庄重剖析解是艰易的.常常近似天认为，矩形角锥喇叭中的电磁场具备球里波个性，而且假设角锥喇叭心径里上的相位分散沿x 战 y 二个目标均为仄圆律变更.按此假设，可写出角锥喇叭的心径场为：ηπβy X R y R x j H y E H e D x E E EH -==+-)2(022)cos(（1.1）如果是尖顶角锥喇叭，则 R H ＝ R E ，可用做尺度删益喇叭.假如楔形喇叭，则R H ≠R E .由此心径里场分散估计的近场与真测的截止符合的很好，道明白假设的心径场分解模型的精确性.2. 辐射场由角锥喇叭的心径场分散，仿照前里供 E 里战 H 里扇形喇叭近区辐射场的步调，便不妨供出角锥喇叭的近区辐射场表白式.由于估计历程较繁，那里间接给出截止.])cos 1([cos 2])cos 1([sin 200H E rj H E rj I I r e E j E I I re E j E θϕλθϕλβϕβθ+=+=-- （2.1） 其中：)]})()([)()({)]}()([)()({(213434)2/(1212)2/(2221u S u S j u C u C e u S u S j u C u C e R I H x H x R j R j H H+-+++-+=--βββββπ （2.3）)]}()([)()({211212)2/(2w S w S j w C w C e R I E Y R j E E +-+=-βββπ（2.4） H x Hx D D /cos sin /cos sin 21πϕθββπϕθββ-=+= (2.5)H H x H HH x H HH x H HH x H R R D u R R D u R R D u R R D u πβββπβββπβββπβββ/)2/(/)2/(/)2/(/)2/(21211111-=+=-=+= (2.6))sin sin 2()sin sin 2(21ϕθπβϕθπβE E E E E E R D R w R D R w -=+= （2.7）角锥喇叭的 E 里战 H 里场为： 02/||====ϕϕπϕθE E E E H E (2.8)正在角锥喇叭的 D E 、R E 、D H 、R H与扇形喇叭的相共时，不妨道明:■角锥喇叭正在 E 里的目标图与 E 里扇形喇叭的 E 里目标图相共；■角锥喇叭正在 H 里内的目标图与 H 里扇形喇叭正在 H 里内的目标图相共.决定(与γ/β =1 ).画出的幅度三维图及 E 里战 H 里目标图如下图所示：是指角锥喇叭的尺寸正在 H 里战 E 里分别与最好，即 λλ2322E Eop H HopD R D R ==43ϕπϕ= (3.1)那样，便可使角锥喇叭的删益为最大.4. 最好角锥喇叭近场 E 里战 H 里的主瓣宽度Z 由于正在相共的 R E 战 D E 条件下， 角锥喇叭的E 里目标图与 E 里扇形喇叭的E 里目标图相共，正在相共的 RH 战 DH 条件下，角锥喇叭的 H 里目标图与 H 里扇形喇叭的目标图相共，则最好角锥喇叭 E 里战 H 里目标图的主瓣宽度分别由式(4.1)战(4.2)表示，即：2θλ/D 1 rad=80λ/D 1(°) (4.1)2θλ/D 1 rad=54λ/D 1(°) (4.2)角锥喇叭做天线时，可按此央供安排.二．角锥喇叭安排真例1.处事频次教号：12060302011000+50+1500=2500MHZ波少λ波导的尺寸a,b应包管波导内只传输TE10波.果此采用λ=λ笔曲极化，电场目标笔曲于大天已给定波束宽度火仄里：2θλ/D1 rad=80λ/D1(°)供得 D1=0.9408m （2θ=10）笔曲里：2θλ/D1 rad=54λ/D1(°)供得 D2=0.42336m （2θ=15）决定尺寸D1，D2喇叭尺寸决定后，由喇叭最好尺寸公式：R H=D12/3λR E=D22/2λ供出喇叭的少度：R HR E对付于角锥喇叭天线，末尾决定其尺寸时，还要思量喇叭有波导正在颈部的尺寸协共问题，如下图所示：代进得到闭系式：考证：而将R E 建改为cm R H 51.2995116.0=9.182451.0212==D D G λπ=45.5 Db表里估计公式：角锥喇叭E 里目标图战H 里目标图分别为对付应的E 里扇形喇叭的E 里目标图战H 里扇形喇叭的H 里目标图.E 里目标图：其中：⎪⎭⎫ ⎝⎛--=θπsin 2222'1R D R k tH 里目标图：其中：⎪⎭⎫ ⎝⎛--=1'11'121R k kD kR t x π dt t x C x ⎰=02)2cos()(π <余弦Fresnel 积分>dt t x S x ⎰=02)2sin()(π<正弦Fresnel 积分> Matlab 源步调：E 里目标图clcclear%a=input('请输进角锥输进端宽度（H 里）单位mm a=') a=8.5;a=a*10.^(-3);%b=input('请输进角锥输进端宽度（E 里）单位mm b=') b=4;b=b*10.^(-3);%D1=input('请输进角锥心径宽度（H 里）单位mm A=') D1=94;D1=D1*10.^(-3);%D2=input('请输进角锥心径宽度（E 里）单位mm B=')D2=42.3;D2=D2*10.^(-3);%h=input('请输进喇叭心少度单位mm H=')h=227;h=h*10.^(-3);%f=input('请输进处事频次单位0.1MHZ f=')f=25500;f=f*10.^6;lamd=3*10.^8/f;R2=h/(1-b/D2);theta=-60:0.2:60;k=2*pi/lamd;theta1=theta.*pi/180;t1_1=sqrt(k/(pi*R2)).*(-(D2/2)-R2.*sin(theta1));t2_1=sqrt(k/(pi*R2)).*((D2/2)-R2.*sin(theta1)); EE=exp(j.*(k.*R2.*(sin(theta1))./2)).*F(t1_1,t2_1); FE=-j.*(a*sqrt(pi*k*R2)/8).*(-(1+cos(theta1))*(2/pi)*(2/pi).*EE);FE1=abs(FE);FE1=FE1./max(FE1);FEdB=20*log10(FE1);figure(1)plot(theta,FEdB);grid ontitle('角锥喇叭E里目标图')xlabel('Angle(\theta)/\ circ')ylabel('Gain(\theta)')H里目标图R1=h/(1-a/D1);theta=-60:0.2:60;k=2*pi/lamd;theta1=theta.*pi/180;kx_1=k.*sin(theta1)+pi/D1;kx_11=k.*sin(theta1)-pi/D1;f1=kx_1.*kx_1*R1/(2*k);f2=kx_11.*kx_11*R1/(2*k);t1_1=sqrt(1/(pi*k*R1)).*(-(k*D1/2)-kx_1*R1);t2_1=sqrt(1/(pi*k*R1)).*((k*D1/2)-kx_1*R1);t1_11=sqrt(1/(pi*k*R1)).*(-(k*D1/2)-kx_11*R1);t2_11=sqrt(1/(pi*k*R1)).*((k*D1/2)-kx_11*R1);FF=exp(j.*f1).*F(t1_1,t2_1)+exp(j.*f2).*F(t1_11,t2_11); FH=j.*(b/8).*sqrt((k*R1/pi)).*((1+cos(theta1)).*FF); FH1=abs(FH);FH1=FH1./max(FH1);FHdB=20*log10(FH1);figure(1)plot(theta,FHdB);grid ontitle('角锥喇叭H里目标图')xlabel('Angle(\theta)/\ circ')ylabel('Gain(\theta)')所用子函数F：%%F(t1,t2)=[C(t2)-C(t1)]-j[S(t2)-S(t1)] function y=F(t1,t2)C2=mfun('FresnelC',t2);C1=mfun('FresnelC',t1);S2=mfun('FresnelS',t2);S1=mfun('FresnelS',t1);y=(C2-C1)-j.*(S2-S1);end。

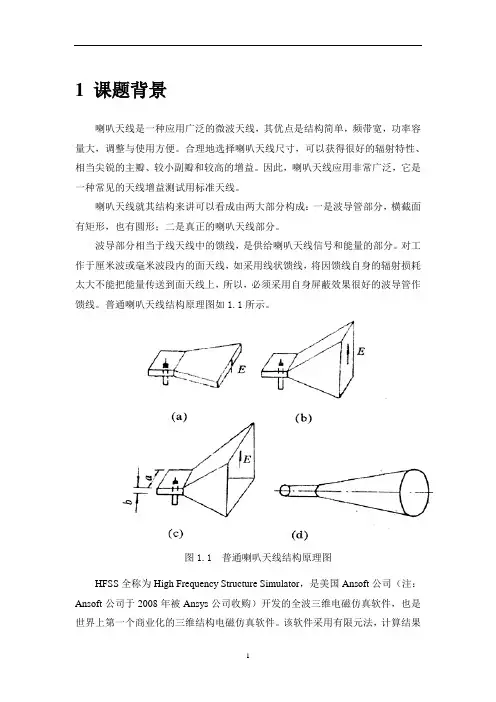
1 课题背景喇叭天线是一种应用广泛的微波天线，其优点是结构简单，频带宽，功率容量大，调整与使用方便。

合理地选择喇叭天线尺寸，可以获得很好的辐射特性、相当尖锐的主瓣、较小副瓣和较高的增益。

因此，喇叭天线应用非常广泛，它是一种常见的天线增益测试用标准天线。

喇叭天线就其结构来讲可以看成由两大部分构成：一是波导管部分，横截面有矩形，也有圆形；二是真正的喇叭天线部分。

波导部分相当于线天线中的馈线，是供给喇叭天线信号和能量的部分。

对工作于厘米波或毫米波段内的面天线，如采用线状馈线，将因馈线自身的辐射损耗太大不能把能量传送到面天线上，所以，必须采用自身屏蔽效果很好的波导管作馈线。

普通喇叭天线结构原理图如1.1所示。

图1.1 普通喇叭天线结构原理图HFSS全称为High Frequency Structure Simulator，是美国Ansoft公司（注：Ansoft公司于2008年被Ansys公司收购）开发的全波三维电磁仿真软件，也是世界上第一个商业化的三维结构电磁仿真软件。

该软件采用有限元法，计算结果精准可靠，是业界公认的三维电磁场设计和分析的工业标准。

HFSS采用标准的Windows图形用户界面，简洁直观；拥有精确自适应的场解器和空前电性能分析能力的功能强大后处理器；能计算任意形状三维无源结构的S参数和全波电磁场；自动化的设计流程，易学易用；稳定成熟的自适应网格剖分技术，结果准确。

使用HFSS，用户只需要创建或导入设计模型，指定模型材料属性，正确分配模型的边界条件和激励，准确定义求解设置，软件便可以计算并输出用户需要的设计结果。

HFSS软件拥有强大的天线设计功能，可以提供全面的天线设计解决方案，是当今天线设计最为流行的软件。

使用HFSS可以仿真分析和优化设计各类天线，能够精确计算天线的各种性能，包括二维、三维远场和近场辐射方向图、天线的方向性系数、S参数、增益、轴比、输入阻抗、电压驻波比、半功率波瓣宽度以及电流分布特性等。

喇叭天线设计范文喇叭天线是一种常见的天线类型，它通过产生和放大电磁波来传输和接收信号。

喇叭天线结构独特，可以提供增益和方向性，使其在许多应用中都表现出色。

在接下来的1200字以上中我们将深入探讨喇叭天线的设计原理和应用。

喇叭天线的设计原理基于天线的形状和尺寸。

它通常由一个底部进口和一个底部出口组成。

进口和出口的大小和形状决定了天线的频率和频带宽度。

进口是天线的输入段，用于接收或发射电磁波。

出口是天线的输出段，用于辐射或接收电磁波。

在进口和出口之间的区域称为导向段，用于引导电磁波。

喇叭天线的设计可以分为两个主要方面：频率响应和辐射特性。

频率响应是指天线在特定频率范围内的工作效果。

喇叭天线的频率响应主要取决于喇叭的形状和尺寸。

为了实现宽带频率响应，天线的进口和出口需要适当的增大。

进口的大小要确保信号的完整性，而出口的大小要确保信号的放大和辐射。

喇叭天线通常用于高频段的应用，例如雷达、通信和卫星通信。

辐射特性是指天线在空间中辐射或接收电磁波的能力。

喇叭天线通常具有良好的方向性，这意味着它可以将信号集中到特定的方向上。

方向性是通过喇叭的形状和导向段的长度来实现的。

较长的导向段可以提高天线的方向性，但也会减少天线的频带宽度。

因此，在设计喇叭天线时需要权衡方向性和频带宽度的需求。

喇叭天线在许多应用中都有广泛的应用。

它们常用于雷达系统中，用于探测和跟踪目标。

喇叭天线在雷达系统中提供了高增益和方向性，能够有效地检测远处的目标。

除了雷达系统，喇叭天线还广泛应用于通信和卫星通信系统中。

它们提供了较好的方向性和覆盖范围，可以实现远距离的数据传输和通信。

设计喇叭天线需要考虑多种因素，例如频率范围、增益、方向性、频带宽度、输入阻抗等。

可以使用各种电磁场模拟软件进行天线设计和分析。

这些软件可以模拟天线的电磁场分布，并提供关于天线性能的详细信息。

此外，实际的天线测试和优化也是设计过程中的重要步骤，可以通过改变天线的形状、尺寸和材料来优化天线的性能。