第一课完全区组设计Friedman 秩和检验

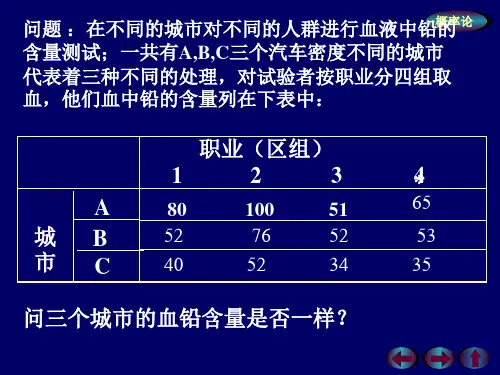
Friedman秩和检验是一种非参数检验方法，主要用于比较多组相关样本的平均值是否存在显著差异。

它适用于样本数据不满足正态分布且样本量较小的情况，不需要假设数据的具体分布情况。

Friedman秩和检验步骤如下：1. 设定假设Friedman秩和检验的原假设为各组样本之间没有显著差异，即总体具有相同的中位数。

备择假设为各组样本之间存在显著差异，总体中位数不完全相同。

2. 计算秩次对每个样本数据按大小顺序排列，并给予秩次，相同数值的样本给予相同的平均秩次，若有并列排名，则按照并列样本的个数进行平均秩次计算。

3. 计算秩和对每组样本数据计算秩和，并计算Friedman秩和检验统计量。

4. 计算检验统计量根据计算所得的秩和，使用Friedman秩和检验的公式，计算检验统计量。

5. 确定显著性水平根据问题的需要，选择显著性水平α，通常取0.05。

6. 查表比较根据样本量和自由度的不同，在Friedman秩和检验的检验表中查找对应的临界值。

7. 判断检验结果比较计算所得的检验统计量与临界值，若大于临界值，则拒绝原假设，认为各组样本之间存在显著差异；若小于临界值，则接受原假设，认为各组样本之间没有显著差异。

在进行Friedman秩和检验时，需要注意的是秩和检验对样本具有独立性要求，不适用于重复数据或者具有时间序列关系的数据。

在对样本数据进行计算时，需要注意样本量的大小和样本之间方差的差异。

Friedman秩和检验是一种适用于非参数检验的方法，适用于样本数据不满足正态分布且样本量较小的情况。

通过以上步骤的计算和比较，可以得出对多组相关样本平均值差异的结论，是一种重要的统计分析方法。

在实际的统计分析中，Friedman秩和检验是一种非常有用的工具，特别适用于需要比较多组相关样本的平均值差异的情况。

接下来将继续对Friedman秩和检验的步骤做更详细的介绍。

第一步：设定假设。

在进行Friedman秩和检验之前，首先需要明确原假设和备择假设。

SPSS教程多个相关样本的Friedman秩和检验及SPSS操作案例来源：中华护理杂志2016年4期⼀．案例评价⼦午流注择时五⾳疗法在慢性⼼⼒衰竭（CHF）焦虑患者中的应⽤效果。

⽅法：将70例CHF焦虑患者随机分为实验组和对照组，各35例，实验组实施⼦午流注择时五⾏⾳乐疗法，对照组实施五⾏⾳乐疗法。

两组在⼲预前、⼲预后4周、8周和12周采⽤匹兹堡睡眠质量指数量表（PSQI）评价睡眠质量。

⼆．说明在之前的介绍中，我们对该研究进⾏了两因素重复测量⽅差分析（案例分析| 两因素重复测量⽅差分析及SPSS操作），并且⽐较了相同组内不同时间的睡眠质量指数量表得分的差异。

对于两组（实验组和对照组）中的任⼀组，若数据服从正态分布，则选⽤单因素重复测量⽅差分析；若数据不服从正态分布，也可以直接进⾏重复测量⽅差分析（尤其是在各组样本量相等或近似相等的情况下，⽽且⾮正态分布实质上并不影响犯I型错误的概率），或者选⽤Friedman秩和检验。

三．SPSS操作1.正态性检验（以实验组得分为例）将所有变量均放⼊因变量列表，点击图，出现如下对话框，勾选含检验的正态图。

2.正态检验结果当样本量较⼩时，推荐使⽤夏⽪洛-威尔克⽅法的正态性检验结果。

由结果得：⼲预前及⼲预后的三次不同时间的得分均不服从正态分布，可以直接进⾏重复测量⽅差，也可以使⽤⾮参数检验，这⾥我们重点介绍Friedman秩和检验。

3.Friedman秩和检验弹出如下对话框：点击上⽅的‘字段’，出现如下对话框，将所有变量均选⼊检验字段。

点击上⽅的‘设置’，出现如下对话框，点击定制检验，在⽐较分布栏选择傅莱德曼检验，多重⽐较选择全部成对。

4.结果解读输出的结果如上图所⽰，结果分别给出了原假设、检验⽅法、显著性以及最后的决策。

由结果可得P<0.001，应该拒绝原假设，即认为实验组在⼲预前、⼲预后4周、8周、12周的得分存在显著性差异。

5.成对⽐较（1）双击上述输出的表格，则可以得到下⾯的界⾯，帮助我们更好的理解假设检验摘要的结果。

Friedman检验-SPSS教程一、问题与数据某研究者拟探讨运动对降低心脏疾病风险的作用。

已知心脏疾病与总胆固醇水平（Total cholesterol，TC）有关，TC水平越高罹患心脏病的风险越大。

因此，该研究者拟分析运动对TC水平的影响，探讨运动与心脏疾病风险的关系。

该研究者招募了10位研究对象，并给予6个月的运动干预，并在干预开始、干预中期（3个月）和干预结束（6个月）时测量研究对象的TC水平，分别记为TC1、TC2和TC3变量。

部分数据如图1。

图1 部分数据二、对问题分析研究者拟判断多组相关数据的变化情况，可以使用Friedman检验。

Friedman 检验可应用于多组配对或相关数据的秩和检验，但需要满足2项假设：假设1：观测变量是连续变量或有序分类变量，如本研究中TC1、TC2和TC3变量均为连续变量。

假设2：具有3个及以上的分组，为配对设计（或各组之间存在相关性）。

经分析，本研究设计符合上述假设，那么应该如何进行Friedman检验呢？三、SPSS操作3.1 Friedman检验在主界面点击 Analyze→Nonparametric Test→Related Samples，确认What is your objective?栏中点选了Automatically compare observed data to hypothesized，如图2。

图2 NonparametricTests: Two or More Related Samples点击Fields→Use custom field assignments，并将TC1、TC2和TC3变量放入Test Fields栏后，点击Run。

如图3。

图3 Fields3.2 计算中位数Friedman检验并不直接给出中位数的具体数值，因此需要单独计算中位数。

在主界面栏中点击Analyze→Compare Means→Means，在Means对话框中，将TC1、TC2和TC3选入Dependent List框中。

在统计学中，Friedman秩和检验是一种非参数检验方法，用于比较三个或三个以上配对样本的均值是否存在显著差异。

它是Wilcoxon符号秩检验的推广，适用于样本量较小或不满足正态分布的情况。

然而，在使用Friedman秩和检验时，有一些注意事项需要我们特别关注。

首先，我们需要注意样本的配对性。

Friedman秩和检验要求样本是配对的，也就是说，每个被试者都需要参与所有的处理条件，或者与其他被试者配对。

如果样本不满足配对条件，那么Friedman秩和检验就不适用。

因此，在进行实验设计时，需要特别注意样本的配对情况，确保满足Friedman秩和检验的前提条件。

其次，我们需要注意样本的独立性。

虽然Friedman秩和检验是一种非参数检验方法，对样本分布的假设要求相对较低，但是它依然要求样本是相互独立的。

也就是说，每个样本的取值不会受到其他样本取值的影响。

在实际应用中，我们需要特别注意样本的独立性，确保数据的有效性。

另外，我们需要注意样本量的大小。

Friedman秩和检验对样本量的要求相对较高，一般来说，每个处理条件至少需要有5个样本。

如果样本量过小，那么Friedman秩和检验的统计结果可能不准确，缺乏说服力。

因此，在进行实验设计时，需要根据样本量的要求，合理安排实验的样本数量。

此外，我们还需要注意对Friedman秩和检验统计结果的解释。

在进行Friedman秩和检验之后，我们需要对统计结果进行正确的解释。

一般来说，如果Friedman秩和检验的p值小于显著性水平（通常取），我们可以拒绝原假设，认为不同处理条件的均值存在显著差异。

如果p值大于显著性水平，我们则无法拒绝原假设，认为不同处理条件的均值没有显著差异。

在解释统计结果时，需要注意不要过度解读，要根据具体情况进行分析。

最后，我们需要注意Friedman秩和检验的局限性。

虽然Friedman秩和检验是一种有用的非参数检验方法，但是它也有一定的局限性。

Friedman秩和检验的使用注意事项Friedman秩和检验是一种非参数统计方法，通常应用于重复测量设计的数据分析中。

它的主要作用是检验不同处理条件下的观测值是否存在显著差异。

但是在使用Friedman秩和检验时，我们需要注意一些事项，以确保结果的准确性和可靠性。

首先，我们需要确保样本的独立性。

在进行Friedman秩和检验之前，我们需要确保样本是独立的，即每个观测值之间的相关性较小。

如果样本之间存在较大的相关性，可能会影响Friedman秩和检验的结果。

因此，在进行实验设计时，我们需要尽量避免使用相关性较大的样本。

其次，我们需要注意样本的大小。

Friedman秩和检验对样本大小有一定的要求，通常需要每个处理条件下的观测值不少于5个。

如果样本大小过小，可能会导致Friedman秩和检验的结果不够可靠。

因此，在进行实验设计时，我们需要尽量保证每个处理条件下的观测值数量足够。

此外，我们还需要注意数据的分布情况。

Friedman秩和检验对数据的分布情况没有要求，即使数据不符合正态分布也可以进行分析。

但是如果数据的分布情况非常偏斜或者存在明显的异常值，可能会影响Friedman秩和检验的结果。

因此，在进行数据分析时，我们需要对数据的分布情况进行检查，并在有必要的情况下进行适当的数据变换或异常值处理。

另外，我们还需要注意Friedman秩和检验的假设条件。

Friedman秩和检验的主要假设包括独立性、同质性和对称性。

在进行Friedman秩和检验之前，我们需要对这些假设条件进行检验，以确保满足这些条件。

如果这些假设条件不满足，可能会影响Friedman秩和检验的结果。

因此，在进行数据分析时，我们需要对Friedman秩和检验的假设条件进行检验，并在有必要的情况下进行适当的调整。

最后，我们需要注意Friedman秩和检验的结果解释。

在进行Friedman秩和检验之后，我们需要对结果进行适当的解释。

特别是当Friedman秩和检验的结果显著时，我们需要进行进一步的事后分析，以确定不同处理条件下的观测值之间的具体差异。