二元函数取极值的条件
- 格式:doc
- 大小:570.50 KB
- 文档页数:2



二元函数极值问题23450x >时,1,z x ∂=∂ 0x <时,1zx∂=-∂. 因此在0x =时偏导数不存在. 由此可见,函数的极值点必为fx∂∂及f y ∂∂同时为零或至少有一个偏导数不存在的点.3.2极值的充分条件设函数),(y x f z =在点的某个邻域内连续且有二阶连续偏导数,又0),(00'=y x f x 且0),(00'=y x fy ,记二阶连续偏导数为Ay x fxx=),(00',By x fxy=),(00',Cy x fyy=),(00',AC B -=∆2,则函数),(y x f z =在),(00y x 点处是否取得极值的条件如下:(1) 当0<∆且0<A 时,函数),(y x f z =在点),(00y x 处取得极大值; (2) 当0<∆且0>A 时,函数),(y x f z =在点),(00y x 处取得极小值; (3) 当0>∆时,函数),(y x f z =在点),(00y x 处不取得极值;(4) 当0=∆时,函数),(y x f z =在点),(00y x 处可能取得极值,也可能不取得极值.4. 求二元函数的极值的步骤要求函数的极值,首先要求出所有使函数的偏导数等于零或偏导数不存在的点,然后讨论该点周围函数的变化情形,以进一步判断是否有极值,为此我们讨论f ∆,若(,)f x y 的一切二阶导数连续,则由泰勒公式并注意到在极值点必须0x y f f ==,就有222000000200001(,)(,)((,)22(,)(,))x xy y f f x x y y f x y f x x y y x f x x y y x y f x x y y y θθθθθθ∆=+∆+∆-=+∆+∆∆++∆+∆∆∆++∆+∆∆.由于(,)f x y 的一切二阶偏导数在00(,)x y 连续,记200(,)x A f x y =,00(,)xy B f x y =,200(,)y C f x y =,那就有6200(,),0(0,0)x f x x y y A x y θθαα+∆+∆=+→∆→∆→00(,),0(0,0)xy f x x y y B x y θθββ+∆+∆=+→∆→∆→200(,),0(0,0)y f x x y y C x y θθγγ+∆+∆=+→∆→∆→于是222211[2][2]22f A x B x y C y x x y y αβγ∆=∆+∆∆+∆+∆+∆∆+∆.当二次形式222kf A x B x y C y =∆+∆∆+∆不为零时,注意到0,0x y ∆→∆→时,,,αβγ都是无穷小量,所以存在点000(,)M x y 的一个领域,使得在这个领域内,f ∆的符号与kf 的符号相同,而当0kf =时,f ∆的符号取决于222x x y y αβγ∆+∆∆+∆的符号了. 对于二次型 222kf A x B x y C y =∆+∆∆+∆ 它的判别式为 2A B H AC B BC==-.那就有以下结论:H>0H<0H=0A<0A>0函数有极大值函数有极小值函数无极值 需进一步判定这是因为当0H >而0A <时,二次型kf 为负定的,故0kf <,从而0f ∆<;当0H >而0A >时,二次型kf 为正定的,故0kf >,从而0f ∆>;当0H <时,二次型为不定的.所以f ∆亦可正可负的,于是函数无极值;当0H =时,二次型kf 在某些,x y ∆∆值上将等于零,于是f ∆的符号就必须进一步判断7了.5. 求极值的相关例题例1 证明具有已知周长的三角形中,等边三角形有最大面积.证明:设三角形的边长为,,x y z ,周长2x y z p ++=,于是2z p x y =--.三角形的面积S 有如下公式:2(,)()()()()()()f x y S p p x p y p z p p x p y x y p==---=--+-. 由 ()(22)0,()(22)0,fp p y p x y xfp p x p x y y ∂=---=∂∂=---=∂解得(,)f x y 的稳定点:(0,)p , (,)p p , (,0)p , 22(,)33p p .事实上,(,)f x y 的定义域是D (如下图阴影部分):yx80x p <<, 0y p <<, x y p +>. (,)f x y 在D 上一定有最大值,在D 内有唯一稳定点22(,)33p p ,4221111(,)***3333327f p p p p p p p ==, (,)f x y 在D ∂上取值为零,因此(,)f x y 一定在22(,)33p p 取到D 内的最大值,即23x p =, 23y p =, 23z p =. 时,三角型有最大值.例2 设通过观测或实验得到一列点(,)i i x y ,1,2,....i n = 它们大体上在一条直线上,即大体上可用直线方程来反映变量x 与y 之间的对应关系,现要确定一直线与这n 个点的偏差平方和最小. 解: 设所求直线方程为y ax b =+,所测得的n 个点为(,)i i x y (1,2...)i n =,现要确定,,a b 使得21(,)()ni i i f a b ax b y ==+-∑为最小,为此112()0,2()0na i i i i nb i ii f x ax b y f ax b y ==⎧=+-=⎪⎪⎨⎪=+-=⎪⎩∑∑ 把这组关于,a b 的线性方程加以整理,得92111.11,n n ni i i i i i i n ni i i i a x b x x y a x bn y =====⎧+=⎪⎪⎨⎪+=⎪⎩∑∑∑∑∑ 求此方程组的解,即得(,)f a b 的稳定点11122111()()n n ni i i ini i i i n ni i i i i n x y x y a y n x x ======-=-∑∑∑∑∑∑ ,211112211()()()()()nnnni i i i i i i i i n ni i i i x y x y x b n x x ======-=-∑∑∑∑∑∑.为了进一步确定该点是极小值点,我们计算得2120naa i i A f x ===>∑,120nab i i B f x ===>∑,2bb C f n ==, 2221144()0n ni i i i D AC B n x x ===-=->∑∑由极值的充要条件知,(,)f a b 在点(,)D a b 取得极小值,由实际问题知这极小值为最小值.结束语多元函数的极值问题在多元函数微分学上有重要应用,在这里利用偏导讨论二元函数极值问题可以帮助我们更好的学习极值问题的求解.参考文献:[1] 廖可人, 李正元. 数学分析[M]. 北京:高等教育出版社, 1986.[2] 陈传璋, 金福临, 朱学炎, 欧阳光中. 数学分析[M].北京:高等教育出版社, 1983. [3] 高尚华. 数学分析[M].北京:高等教育出版社,2001.10。

二元函数取极值的充分条件二元函数取极值的充分条件分为以下几种情况:1. 二次型矩阵的正负性:设二元函数 $f(x,y)$ 在点 $(x_0,y_0)$ 附近有连续的二阶偏导数,且$\Delta H=f_{xx}(x_0,y_0)f_{yy}(x_0,y_0)-[f_{xy}(x_0,y_0)]^2>0$。
则当 $f_{xx}(x_0,y_0)>0$ 时,$f(x,y)$ 在点 $(x_0,y_0)$ 取极小值;当$f_{xx}(x_0,y_0)<0$ 时,$f(x,y)$ 在点 $(x_0,y_0)$ 取极大值。
2. 一阶偏导数的消失:设二元函数 $f(x,y)$ 在点 $(x_0,y_0)$ 附近有连续的偏导数,且$f_x(x_0,y_0)=0$,$f_y(x_0,y_0)=0$,则 $(x_0,y_0)$ 是 $f(x,y)$ 的一个驻点。
仅凭一阶偏导数消失的条件不能判断极值,需进一步判断。
3. 二阶导数的正负性:设二元函数 $f(x,y)$ 在点 $(x_0,y_0)$ 附近有连续的二阶偏导数,且$f_x(x_0,y_0)=0$,$f_y(x_0,y_0)=0$。
(1) 若 $f_{xx}(x_0,y_0)>0$ 且 $\Delta H>0$,则 $(x_0,y_0)$ 是$f(x,y)$ 的极小值点。
(2) 若 $f_{xx}(x_0,y_0)<0$ 且 $\Delta H>0$,则 $(x_0,y_0)$ 是$f(x,y)$ 的极大值点。
(3) 若 $\Delta H<0$,则 $(x_0,y_0)$ 不是 $f(x,y)$ 的极值点。
(4) 若 $\Delta H=0$,则无法判断 $(x_0,y_0)$ 是否是 $f(x,y)$ 的极值点,需作进一步研究。
4. 鞍点与拐点:当 $\Delta H<0$ 时, $(x_0,y_0)$ 不是 $f(x,y)$ 的极值点。

2.二元函数的极值与最值二元函数的极值与最值问题已成为近年考研的重点, 现对二元函数的极值与 最值的求法总结如下: 1.二元函数的无条件极值 (1) 二元函数的极值一定在 驻点 和不可导点 取得。
对于不可导点,难以判断 是否是极值点;对于驻点可用极值的充分条件判定。
(2)二元函数取得极值的 必要条件 : 设 z f (x,y) 在点(x 0,y 0) 处可微分且在 点(x 0, y 0 )处有极值,则 f 'x (x 0,y 0) 0, f 'y (x 0, y 0) 0,即 (x 0,y 0) 是驻点。
(3) 二元函数取得极值的 充分条件 :设 z f (x,y) 在(x 0,y 0) 的某个领域内有 连续上 二阶偏导数,且 f 'x (x 0,y 0) f 'y (x 0, y 0) 0 ,令 f'xx (x 0,y 0) A , f'xy (x 0,y 0) B , f 'yy (x 0,y 0) C ,则当B 2AC 0且 A<0 时, f ( x 0 , y 0 )为极大值; 当B 2 AC 0且 A>0, f ( x 0 , y 0 )为极小值; B 2 AC 0 时,(x 0, y 0) 不是极值点。
注意: 当 B 2-AC = 0时,函数 z = f (x, y)在点( x 0 , y 0 )可能有极值,也可能没有 极值,需另行讨论 例 1 求函数 z = x 3 + y 2- 2xy 的极值. 【分析】可能极值点是两个一阶偏导数为零的点, 先求出一阶偏导, 再令其为零 确定极值点即可, 然后用二阶偏导确定是极大值还是极小值, 【解】先求函数的一、二阶偏导数:并求出相应的极值 . 2z 2 z z 3x 2y , 2y 2x . 26x ,xy x2zxy2z2y 2再求函数的驻点.令 z= 0,x得方程组23x 2y 0, 2y 2x 0.22求得驻点(0,0)、( 2,2).33利用定理 2 对驻点进行讨论:2.(1)对驻点(0, 0),由于 A = 0, B =-2, C = 2,B 2-AC 0,故(0, 0)不是函数 z = f(x, y) 的极值点.(2)对驻点( 2,2),由于 A =4, B =-2,C = 2,B 2-AC =-4 0, 且A 0,则 332 2 4 f ( 2,2) 4为函数的一个极小值.3 3 27例 2:( 2004数学一)设 z=z(x,y)是由 x 26xy 10 y 22yz z 218 0 确定的函 数,求 z z(x, y )的极值点和极值 .分析 】 本题把极值问题与隐函数求导方法相结合,计算量是比较大的。

⼆元函数极值Δ=AC-B²
判断⼆元函数极值⽅法如下:
设:⼆元函数 f(x,y)的稳定点为:(x0,y0),
即:∂f(x0,y0)/∂x = ∂f(x0,y0)/∂y = 0;
记::A=∂²f(x0,y0)/∂x²
B=∂²f(x0,y0)/∂x∂y
C=∂²f(x0,y0)/∂y²
Δ=AC-B²
如果:Δ>0
A0,f(x0,y0) 为极⼩值4102;
如果:Δ0
f(0,0)=0 为最⼩1653值。
求解函数极值⽅法:寻求函数整个定义域上的最⼤值和最⼩值是数学优化的⽬标。
如果函数在闭合区间上是连续的,则通过极值定理存在整个定义域上的最⼤值和最⼩值。
此外,整个定义域上最⼤值(或最⼩值)必须是域内部的局部最⼤值(或最⼩值),或必须位于域的边界上。
扩展资料
判断函数极值定义:
若函数f(x)在x₀的⼀个邻域D有定义,且对D中除x₀的所有点,都有f(x)<f(x₀),则称f(x₀)是函数f(x)的⼀个极⼤值。
同理,若对D的所有点,都有f(x)>f(x₀),则称f(x₀)是函数f(x)的⼀个极⼩值。
极值的概念来⾃数学应⽤中的最⼤最⼩值问题。
根据极值定律,定义在⼀个有界闭区域上的每⼀个连续函数都必定达到它的最⼤值和最⼩值,问题在于要确定它在哪些点处达到最⼤值或最⼩值。
如果极值点不是边界点,就⼀定是内点。
因此,这⾥的⾸要任务是求得⼀个内点成为⼀个极值点的必要条件。


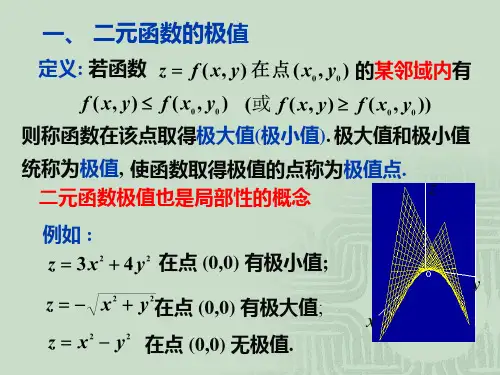


二元函数的极值与最值在数学中,二元函数是一个带有两个自变量的函数,通常表示为f(x, y),其中x和y分别是独立变量。
当我们定义一个函数时,我们通常希望找到函数的最大和最小值等重要信息。
在这篇文章中,我们将探讨二元函数的极值点和最值点,以及如何找到它们。
极值和最值的概念首先,我们需要了解的是“极值”和“最值”的概念。
在微积分中,极值是指在一个函数曲线上的局部最大值或最小值。
具体地说,一个函数在一个点上的导数为零,这个点就是函数的驻点。
如果该点是一个局部最大值或最小值,则它是该函数的一个极值点。
最值是在函数的定义域内找到的最大值或最小值。
二元函数的极值点要找到二元函数的极值点,我们需要找到函数曲面上的局部最大值或最小值。
这意味着我们需要找到函数曲面上的所有可能的驻点。
与一元函数类似,我们可以使用偏导数来找到驻点。
因此,对于二元函数f(x, y),我们可以用以下公式来计算它的偏导数:∂f/∂x = 0 和∂f/∂y = 0这些方程可以帮助我们找到一个或多个可能的驻点。
然而,这些驻点可能是最大值或者最小值,或者它们根本不是。
我们还需要使用二阶偏导数来确定驻点的角色。
如果二阶偏导数是:1. 正的,那么这个点是局部最小值点。
2. 负的,那么这个点是局部最大值点。
3. 0,那么这个点不是极点。
最终,我们将找到所有可能的极值点,以及它们的角色和函数值。
二元函数的最值点要找到二元函数的最大值和最小值,我们要按照以下步骤进行:1. 找到函数曲面上的所有极值点2. 在函数的定义域内找到函数曲面上的所有最大值和最小值。
3. 在找到的所有值中找到全局最大值和最小值。
在这个过程中,我们需要使用一些数学方法来找到最大值和最小值。
最常见的方法是使用拉格朗日乘数法。
拉格朗日乘数法拉格朗日乘数法是一种用于最值问题的数学方法。
这个方法的基本思想是,如果一个函数f(x, y)在限制条件g(x, y)下取得最大值或最小值,那么这个点的梯度向量(∇f)和限制条件的梯度向量(∇g)之间应该是平行的。
二元函数极值证明二元函数的极值是数学中非常重要的概念,在应用数学、物理学、经济学等领域都有广泛的应用。
本文将介绍二元函数极值的定义、判断和求解方法,并分析其应用情况。
一、二元函数极值的定义二元函数指的是含有两个自变量的函数,通常表示为 f(x, y)。
对于二元函数而言,极值点是函数表现出局部最大或最小值的点。
极大值点指的是局部最大值点,而极小值点则指局部最小值点。
二、二元函数的极值判断二元函数的极值判断通常有两种方法:一是通过一阶偏导数和二阶偏导数判断,二是通过海森矩阵判断。
下面将分别对两种方法进行介绍。
1. 通过一阶偏导数和二阶偏导数判断偏导数是求解极值的重要工具,需要根据偏导数的符号来判断二元函数的极值。
一阶偏导数的符号判断:当 f_x=0, f_y=0 时,存在驻点(也就是可能的最值点)。
当 f_x>0, f_y>0 时,f(x, y) 与 f(x-dx, y-dy) 的值相等,则(x, y) 不是极值点。
当 f_x<0, f_y<0 时,f(x, y) 与 f(x+dx, y+dy) 的值相等,则(x, y) 不是极值点。
当 f_x>0, f_y<0 时,f(x, y) 的 f_y 方向导数为负,则 (x, y) 是极大值点;反之 f(x, y) 的 f_x 方向导数为正,则 (x, y) 是极小值点。
当 f_x<0, f_y>0 时,f(x, y) 的 f_y 方向导数为正,则 (x, y) 是极小值点;反之 f(x, y) 的 f_x 方向导数为负,则 (x, y) 是极大值点。
二阶偏导数的符号判断:当 f_xx < 0 且 f_xy^2 > f_xx*f_yy 时,(x, y) 为极大值点;反之,当 f_xx > 0 且 f_xy^2 > f_xx*f_yy 时,(x, y) 为极小值点。
2. 通过海森矩阵判断海森矩阵是判断函数极值的另一个工具,需要根据海森矩阵的特性判断二元函数的极值。
二元函数取极值的条件
判断二元函数极值方法如下:
设:二元函数f(x,y)的稳定点为:(x0,y0),
即:∂f(x0,y0)/∂x = ∂f(x0,y0)/∂y = 0;
记::A=∂²f(x0,y0)/∂x²
B=∂²f(x0,y0)/∂x∂y
C=∂²f(x0,y0)/∂y²
∆=AC-B²
如果:∆>0
A0,f(x0,y0) 为极小值;
如果:∆0
f(0,0)=0 为最小值。
求解函数极值方法:寻求函数整个定义域上的最大值和最小值是数学优化的目标。
如果函数在闭合区间上是连续的,则通过极值定理存在整个定义域上的最大值和最小值。
此外,整个定义域上最大值(或最小值)必须是域内部的局部最大值(或最小值),或必须位于域的边界上。
扩展资料
判断函数极值定义:
若函数f(x)在x₀的一个邻域D有定义,且对D中除x₀的所有点,都有f(x)<f(x ₀),则称f(x₀)是函数f(x)的一个极大值。
同理,若对D的所有点,都有f(x)>f(x ₀),则称f(x₀)是函数f(x)的一个极小值。
极值的概念来自数学应用中的最大最小值问题。
根据极值定律,定义在一个有界闭区域上的每一个连续函数都必定达到它的最大值和最小值,问题在于要确定它在哪些点处达到最大值或最小值。
如果极值点不是边界点,就一定是内点。
因此,这里的首要任务是求得一个内点成为一个极值点的必要条件。