二元函数的极值问题
- 格式:doc
- 大小:947.50 KB
- 文档页数:17

⼆元函数的极值与最值问题
⽬录
写在最前
对于形如z=f(x,y)的函数,求解极值的通法⼀般有两种:
偏导数法
⼆元全微分法
由于偏导数法操作简单,下⾯仅介绍这种⽅法
⼆元函数极值点
Ops:只想知道最值的可以跳过这⼀节。
我们以驻点为圆⼼在xy平⾯上做⼀个圆(就如同在⼀元函数y=f(x)驻点附近找⼀段区间),若当半径⾜够⼩时,f(x0,y0)是该圆形区域的最⼤值或最⼩值, 那么该驻点就是极⼤值点或极⼩值点。
与⼀元函数类似,驻点不⼀点是极值点。
那么我们如何判断极点呢?
⼀个⽐较常规的想法是,让f x在x=x0的两边异号,让f y在y=y0的两边异号,借此来判断函数的极值点。
但有⼀个很明显的错误:
类⽐地理中的鞍部,这个点被称作鞍点。
那么,该怎么做呢,数学家想到了⼀种⽅法——⼆阶偏导法。
令
A=f xx(x0,y0),B=f xy(x0,y0),C=f yy(x0,y0)
则有
A×C−B2>0且A>0==>极⼩值
A×C−B2>0且A<0==>极⼤值
A×C−B2<0==>鞍点
A×C−B2==0==>⽆法确定
⼆元函数最值
最值问题和极值问题相⽐,最⼤的区别就是最值问题可以通过⽐较各点的值来计算。
我们可以通过求出所有极值点甚⾄⾮极值点的值来得出最终的答案。
既然如此,我们可以求出所有可能的点(各偏导等于零的点)并计算得到最终答案。

二元函数的极值点
二元函数的极值点是指这个函数在某一点上取得最大值或最小值的点。
要求二元函数的极值点,需要先求出这个函数的偏导数。
如果函数是连续的,那么它的极值点就是它的偏导数为 0 的点。
如果这个函数是可微的,那么这个函数的极值点就是它的偏导数为 0 或者不存在的点。
求出了偏导数之后,就可以用二元函数的一阶条件来判断这个点是极大值点还是极小值点。
具体来说,如果二元函数 f(x, y) 在点 (x0, y0) 处的偏导数为 0,那么如果二元函数的海森矩阵 H(x0, y0) 在这个点处的行列式大于 0,那么这个点就是极小值点;如果行列式小于 0,那么这个点就是极大值点;如果行列式等于 0,那么这个点可能是极值点,也可能不是。
二元函数取极值的条件
判断二元函数极值方法如下:
设:二元函数f(x,y)的稳定点为:(x0,y0),
即:∂f(x0,y0)/∂x = ∂f(x0,y0)/∂y = 0;
记::A=∂²f(x0,y0)/∂x²
B=∂²f(x0,y0)/∂x∂y
C=∂²f(x0,y0)/∂y²
∆=AC-B²
如果:∆>0
A0,f(x0,y0) 为极小值;
如果:∆0
f(0,0)=0 为最小值。
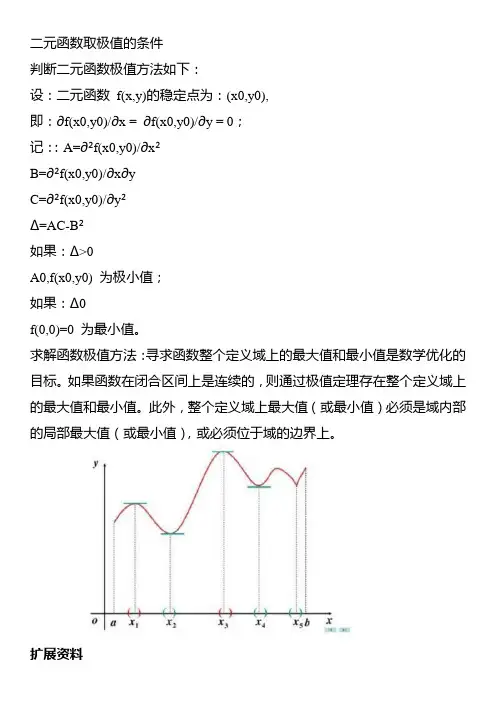
求解函数极值方法:寻求函数整个定义域上的最大值和最小值是数学优化的目标。
如果函数在闭合区间上是连续的,则通过极值定理存在整个定义域上的最大值和最小值。
此外,整个定义域上最大值(或最小值)必须是域内部的局部最大值(或最小值),或必须位于域的边界上。
扩展资料
判断函数极值定义:
若函数f(x)在x₀的一个邻域D有定义,且对D中除x₀的所有点,都有f(x)<f(x ₀),则称f(x₀)是函数f(x)的一个极大值。
同理,若对D的所有点,都有f(x)>f(x ₀),则称f(x₀)是函数f(x)的一个极小值。
极值的概念来自数学应用中的最大最小值问题。
根据极值定律,定义在一个有界闭区域上的每一个连续函数都必定达到它的最大值和最小值,问题在于要确定它在哪些点处达到最大值或最小值。
如果极值点不是边界点,就一定是内点。
因此,这里的首要任务是求得一个内点成为一个极值点的必要条件。

二元函数极值问题23450x >时,1,z x ∂=∂ 0x <时,1zx∂=-∂. 因此在0x =时偏导数不存在. 由此可见,函数的极值点必为fx∂∂及f y ∂∂同时为零或至少有一个偏导数不存在的点.3.2极值的充分条件设函数),(y x f z =在点的某个邻域内连续且有二阶连续偏导数,又0),(00'=y x f x 且0),(00'=y x fy ,记二阶连续偏导数为Ay x fxx=),(00',By x fxy=),(00',Cy x fyy=),(00',AC B -=∆2,则函数),(y x f z =在),(00y x 点处是否取得极值的条件如下:(1) 当0<∆且0<A 时,函数),(y x f z =在点),(00y x 处取得极大值; (2) 当0<∆且0>A 时,函数),(y x f z =在点),(00y x 处取得极小值; (3) 当0>∆时,函数),(y x f z =在点),(00y x 处不取得极值;(4) 当0=∆时,函数),(y x f z =在点),(00y x 处可能取得极值,也可能不取得极值.4. 求二元函数的极值的步骤要求函数的极值,首先要求出所有使函数的偏导数等于零或偏导数不存在的点,然后讨论该点周围函数的变化情形,以进一步判断是否有极值,为此我们讨论f ∆,若(,)f x y 的一切二阶导数连续,则由泰勒公式并注意到在极值点必须0x y f f ==,就有222000000200001(,)(,)((,)22(,)(,))x xy y f f x x y y f x y f x x y y x f x x y y x y f x x y y y θθθθθθ∆=+∆+∆-=+∆+∆∆++∆+∆∆∆++∆+∆∆.由于(,)f x y 的一切二阶偏导数在00(,)x y 连续,记200(,)x A f x y =,00(,)xy B f x y =,200(,)y C f x y =,那就有6200(,),0(0,0)x f x x y y A x y θθαα+∆+∆=+→∆→∆→00(,),0(0,0)xy f x x y y B x y θθββ+∆+∆=+→∆→∆→200(,),0(0,0)y f x x y y C x y θθγγ+∆+∆=+→∆→∆→于是222211[2][2]22f A x B x y C y x x y y αβγ∆=∆+∆∆+∆+∆+∆∆+∆.当二次形式222kf A x B x y C y =∆+∆∆+∆不为零时,注意到0,0x y ∆→∆→时,,,αβγ都是无穷小量,所以存在点000(,)M x y 的一个领域,使得在这个领域内,f ∆的符号与kf 的符号相同,而当0kf =时,f ∆的符号取决于222x x y y αβγ∆+∆∆+∆的符号了. 对于二次型 222kf A x B x y C y =∆+∆∆+∆ 它的判别式为 2A B H AC B BC==-.那就有以下结论:H>0H<0H=0A<0A>0函数有极大值函数有极小值函数无极值 需进一步判定这是因为当0H >而0A <时,二次型kf 为负定的,故0kf <,从而0f ∆<;当0H >而0A >时,二次型kf 为正定的,故0kf >,从而0f ∆>;当0H <时,二次型为不定的.所以f ∆亦可正可负的,于是函数无极值;当0H =时,二次型kf 在某些,x y ∆∆值上将等于零,于是f ∆的符号就必须进一步判断7了.5. 求极值的相关例题例1 证明具有已知周长的三角形中,等边三角形有最大面积.证明:设三角形的边长为,,x y z ,周长2x y z p ++=,于是2z p x y =--.三角形的面积S 有如下公式:2(,)()()()()()()f x y S p p x p y p z p p x p y x y p==---=--+-. 由 ()(22)0,()(22)0,fp p y p x y xfp p x p x y y ∂=---=∂∂=---=∂解得(,)f x y 的稳定点:(0,)p , (,)p p , (,0)p , 22(,)33p p .事实上,(,)f x y 的定义域是D (如下图阴影部分):yx80x p <<, 0y p <<, x y p +>. (,)f x y 在D 上一定有最大值,在D 内有唯一稳定点22(,)33p p ,4221111(,)***3333327f p p p p p p p ==, (,)f x y 在D ∂上取值为零,因此(,)f x y 一定在22(,)33p p 取到D 内的最大值,即23x p =, 23y p =, 23z p =. 时,三角型有最大值.例2 设通过观测或实验得到一列点(,)i i x y ,1,2,....i n = 它们大体上在一条直线上,即大体上可用直线方程来反映变量x 与y 之间的对应关系,现要确定一直线与这n 个点的偏差平方和最小. 解: 设所求直线方程为y ax b =+,所测得的n 个点为(,)i i x y (1,2...)i n =,现要确定,,a b 使得21(,)()ni i i f a b ax b y ==+-∑为最小,为此112()0,2()0na i i i i nb i ii f x ax b y f ax b y ==⎧=+-=⎪⎪⎨⎪=+-=⎪⎩∑∑ 把这组关于,a b 的线性方程加以整理,得92111.11,n n ni i i i i i i n ni i i i a x b x x y a x bn y =====⎧+=⎪⎪⎨⎪+=⎪⎩∑∑∑∑∑ 求此方程组的解,即得(,)f a b 的稳定点11122111()()n n ni i i ini i i i n ni i i i i n x y x y a y n x x ======-=-∑∑∑∑∑∑ ,211112211()()()()()nnnni i i i i i i i i n ni i i i x y x y x b n x x ======-=-∑∑∑∑∑∑.为了进一步确定该点是极小值点,我们计算得2120naa i i A f x ===>∑,120nab i i B f x ===>∑,2bb C f n ==, 2221144()0n ni i i i D AC B n x x ===-=->∑∑由极值的充要条件知,(,)f a b 在点(,)D a b 取得极小值,由实际问题知这极小值为最小值.结束语多元函数的极值问题在多元函数微分学上有重要应用,在这里利用偏导讨论二元函数极值问题可以帮助我们更好的学习极值问题的求解.参考文献:[1] 廖可人, 李正元. 数学分析[M]. 北京:高等教育出版社, 1986.[2] 陈传璋, 金福临, 朱学炎, 欧阳光中. 数学分析[M].北京:高等教育出版社, 1983. [3] 高尚华. 数学分析[M].北京:高等教育出版社,2001.10。


2.二元函数的极值与最值二元函数的极值与最值问题已成为近年考研的重点, 现对二元函数的极值与 最值的求法总结如下: 1.二元函数的无条件极值 (1) 二元函数的极值一定在 驻点 和不可导点 取得。
对于不可导点,难以判断 是否是极值点;对于驻点可用极值的充分条件判定。
(2)二元函数取得极值的 必要条件 : 设 z f (x,y) 在点(x 0,y 0) 处可微分且在 点(x 0, y 0 )处有极值,则 f 'x (x 0,y 0) 0, f 'y (x 0, y 0) 0,即 (x 0,y 0) 是驻点。
(3) 二元函数取得极值的 充分条件 :设 z f (x,y) 在(x 0,y 0) 的某个领域内有 连续上 二阶偏导数,且 f 'x (x 0,y 0) f 'y (x 0, y 0) 0 ,令 f'xx (x 0,y 0) A , f'xy (x 0,y 0) B , f 'yy (x 0,y 0) C ,则当B 2AC 0且 A<0 时, f ( x 0 , y 0 )为极大值; 当B 2 AC 0且 A>0, f ( x 0 , y 0 )为极小值; B 2 AC 0 时,(x 0, y 0) 不是极值点。
注意: 当 B 2-AC = 0时,函数 z = f (x, y)在点( x 0 , y 0 )可能有极值,也可能没有 极值,需另行讨论 例 1 求函数 z = x 3 + y 2- 2xy 的极值. 【分析】可能极值点是两个一阶偏导数为零的点, 先求出一阶偏导, 再令其为零 确定极值点即可, 然后用二阶偏导确定是极大值还是极小值, 【解】先求函数的一、二阶偏导数:并求出相应的极值 . 2z 2 z z 3x 2y , 2y 2x . 26x ,xy x2zxy2z2y 2再求函数的驻点.令 z= 0,x得方程组23x 2y 0, 2y 2x 0.22求得驻点(0,0)、( 2,2).33利用定理 2 对驻点进行讨论:2.(1)对驻点(0, 0),由于 A = 0, B =-2, C = 2,B 2-AC 0,故(0, 0)不是函数 z = f(x, y) 的极值点.(2)对驻点( 2,2),由于 A =4, B =-2,C = 2,B 2-AC =-4 0, 且A 0,则 332 2 4 f ( 2,2) 4为函数的一个极小值.3 3 27例 2:( 2004数学一)设 z=z(x,y)是由 x 26xy 10 y 22yz z 218 0 确定的函 数,求 z z(x, y )的极值点和极值 .分析 】 本题把极值问题与隐函数求导方法相结合,计算量是比较大的。

二元函数 f(x,y) 求最值的常用解题方法求解二元函数f(x,y)最值的常用解题方法求解二元函数f(x,y)的最值是高等数学课程中的一道应用难题,通过求解最值问题,可以得出函数f(x,y)的最大值和最小值,以此来分析函数的极值的特征,为其他数学问题的求解提供思路。
下文着重介绍十常用的解决二元函数最值问题的方法:第一种方法是从图形观察法,即通过观察函数f(x,y)的图像,可以直接看出函数的最大值和最小值。
但这一方法有明显的局限性,仅对那些图像清晰简明容易看出极值的二元函数有效。
第二种方法基于极大值极小值原理。
据该原理推测,函数f(x,y)的最值必定出现在函数的定义域中,该函数的极大值与极小值的数值点满足一定的不等式。
第三种方法利用二阶偏导数法。
由二阶偏导数的值判断该函数的极值性质,对于极值的求解,可以通过求解一元函数的一阶导数与二阶导数等于零的根来实现。
第四种方法是利用拉格朗日函数法。
它依赖拉格朗日函数以及拉格朗日不等式,依据拉格朗日不等式,可以确定函数f(x,y)的极值,拉格朗日不等式中的拉格朗日函数应是原函数的真实性函数。
第五种方法是利用泰勒级数近似法。
这种方法可以有效简化复杂的二元函数,将其分解微小量的和,以此来求解函数f(x,y)的极值。
第六种方法是利用几何法求解最值问题。
这一方法是将二元函数转化成平面几何中的曲线,求解曲线相交,以求解函数极值问题。
第七种方法是利用拉普拉斯法求解最值问题。
依据拉普拉斯定理,函数f(x,y)的最值定义域内满足微分方程组,而拉普拉斯方法便是利用该定理求解最值的有效方法之一。
第八种方法也可以通过牛顿-拉夫逊迭代法确定二元函数f(x,y)的最值。
它借助损失函数与多元函数,以此来求解极值exx让高维函数从有限纸面集梳理、。

二元函数极值点的判别条件
定义设二元函数z=f(x,y)的定义域为D,点M0(x0,y0)(M∈D)的某一邻域在D内有定义,对于该邻域内异于M0的任何点(x,y),如果f(x,y)> f(xo,yo),则称点Mo(x,yo)是函数z=f(x,y)的一个极小值点,称f(x0,yo)为函数z=f(x,y)的一个极小值.如果f(x,y)< f(xo, yo),则称点Mo(xo,yo)是函数z=f(x,y)的一个极大值点,称f(xo,yo)为函数z=f(x,y)的一个极大值。
极小值点和极大值点统称极值点;极小值和极大值统称极值。
显然,如果二元函数z=f(x,y)在点(xo,yo)取得极值,则一元函数z=f(x,yo)在点x取得极值,一元函数z=f(xo,y)在点yo取得极值,此得到极值点的必要条件。
定理1(必要条件)设二元函数z=f(x,y)在点(xo,yo)取得极值,且fx(xo,yo),fy(o,yo)存在,则fx(xo,yo)=0,fy(xo,yo)=0。
称两个偏导数都为0的点为二元函数z=f(x,y)的驻点,驻点不一定就是极值点(充分条件)设二元函数z=f(x,y)在点Mo(xo,yo)的某一邻域内连续,且有连续的一二阶偏导数,又Mo(xo,yo)是驻点,令则
(1)当△<0时,点Mo(x,yo)是极值点.且当A<0时,点Mo(xo,yo)是极大值点;当A>0时,Mo(x,y)是极小值点;
(2)当△>0时,点Mo(x0,y)不是极值点;
(3)当△=0时,Mo(x,yo)可能是极值点,也可能不是极值点,需另作讨论。

二元函数的极值和最值二元函数是指含有两个未知变量的函数,通常用z=f(x,y)来表示。
当x、y取不同的值时,z的取值也会发生变化,因此我们需要研究如何找出二元函数的极值和最值。
一、定义首先,我们需要了解极值和最值的定义。
极值是指函数在某个点上取得的极大值或极小值,而最值则是指函数在定义域内取得的最大值或最小值。
在二元函数中,极值也分为极大值和极小值。
当函数在某个点处取得极大值时,这个点被称为极大值点;同理,当函数在某个点处取得极小值时,这个点被称为极小值点。
考虑以下例子:z=x^2+y^2,我们需要找到z的极小值和最小值。
二、求解方法我们可以通过求一阶偏导数来找到极值点和最值点。
对于二元函数z=f(x,y),我们先求出x和y的一阶偏导数:∂z/∂x=2x∂z/∂y=2y求出它们的偏导数后,我们需要将偏导数相等的方程组联立起来,解出x和y的值,进而求得z的值。
举个例子,对于函数z=x^2+y^2,我们可以得到:2x=02y=0由此可得,当x=0,y=0时,z取得最小值0。
除了求一阶偏导数的方法,我们还可以通过求二阶偏导数来判断函数的极值类型。
若f(x0,y0)满足:① ∂²f/∂x²(x0,y0)>0, ∂²f/∂y²(x0,y0)>0,则f(x0,y0)为极小值点;② ∂²f/∂x²(x0,y0)<0, ∂²f/∂y²(x0,y0)<0,则f(x0,y0)为极大值点;③ ∂²f/∂x²(x0,y0)与∂²f/∂y²(x0,y0)符号相反,则f(x0,y0)为鞍点。
同样以z=x^2+y^2为例,我们可以得到:∂²z/∂x²=∂²z/∂y²=2>0,因此z取得最小值。
3. 拓展方法除了上述两种方法外,我们还可以利用拉格朗日乘数法,求出约束条件下的极值和最值。

⼆元函数极值Δ=AC-B²
判断⼆元函数极值⽅法如下:
设:⼆元函数 f(x,y)的稳定点为:(x0,y0),
即:∂f(x0,y0)/∂x = ∂f(x0,y0)/∂y = 0;
记::A=∂²f(x0,y0)/∂x²
B=∂²f(x0,y0)/∂x∂y
C=∂²f(x0,y0)/∂y²
Δ=AC-B²
如果:Δ>0
A0,f(x0,y0) 为极⼩值4102;
如果:Δ0
f(0,0)=0 为最⼩1653值。
求解函数极值⽅法:寻求函数整个定义域上的最⼤值和最⼩值是数学优化的⽬标。
如果函数在闭合区间上是连续的,则通过极值定理存在整个定义域上的最⼤值和最⼩值。
此外,整个定义域上最⼤值(或最⼩值)必须是域内部的局部最⼤值(或最⼩值),或必须位于域的边界上。
扩展资料
判断函数极值定义:
若函数f(x)在x₀的⼀个邻域D有定义,且对D中除x₀的所有点,都有f(x)<f(x₀),则称f(x₀)是函数f(x)的⼀个极⼤值。
同理,若对D的所有点,都有f(x)>f(x₀),则称f(x₀)是函数f(x)的⼀个极⼩值。
极值的概念来⾃数学应⽤中的最⼤最⼩值问题。
根据极值定律,定义在⼀个有界闭区域上的每⼀个连续函数都必定达到它的最⼤值和最⼩值,问题在于要确定它在哪些点处达到最⼤值或最⼩值。
如果极值点不是边界点,就⼀定是内点。
因此,这⾥的⾸要任务是求得⼀个内点成为⼀个极值点的必要条件。

二元函数用海塞矩阵判断极值在数学中,函数的极值是一种特殊的点,它在该函数的定义域内取得函数值的最大值或最小值。
对于二元函数,也就是含有两个自变量的函数,我们可以使用海塞矩阵来判断其极值。
海塞矩阵是一个二阶偏导数矩阵,用来描述函数在某点附近的局部曲率性质。
对于二元函数f(x,y),其海塞矩阵H定义为:H = [ fxx fxy ][ fyx fyy ]其中,fxx表示f对x的二阶偏导数,fxy表示f对x和y的混合二阶偏导数,fyx表示f对y和x的混合二阶偏导数,fyy表示f对y 的二阶偏导数。
在判断二元函数的极值时,我们可以使用海塞矩阵的特征值来进行分析。
具体来说,如果海塞矩阵的所有特征值都大于0,那么该点是函数的极小值点;如果海塞矩阵的所有特征值都小于0,那么该点是函数的极大值点;如果海塞矩阵的特征值有正有负,那么该点既不是极小值点也不是极大值点,而是鞍点。
通过上述分析,我们可以得出以下结论:如果二元函数的海塞矩阵的所有特征值都大于0或都小于0,则该函数在该点附近存在极值;如果海塞矩阵的特征值有正有负,则该函数在该点附近存在鞍点。
使用海塞矩阵判断二元函数的极值的步骤如下:1. 计算二元函数的一阶偏导数和二阶偏导数;2. 根据一阶偏导数和二阶偏导数计算海塞矩阵;3. 计算海塞矩阵的特征值;4. 判断特征值的符号,确定函数在该点附近的性质。
需要注意的是,海塞矩阵只能在函数的定义域内的光滑区域使用,即函数在该点的一阶偏导数存在且连续。
让我们通过一个例子来进一步理解如何使用海塞矩阵判断二元函数的极值。
考虑二元函数f(x,y) = x^2 + y^2 - 2xy - 2x - 2y + 3。
我们首先计算一阶偏导数和二阶偏导数:f_x = 2x - 2y - 2f_y = 2y - 2x - 2f_{xx} = 2f_{xy} = -2f_{yx} = -2f_{yy} = 2接下来计算海塞矩阵:H = [2 -2][-2 2]计算海塞矩阵的特征值:|H - λI| = (2 - λ)(2 - λ) - (-2)(-2) = (2 - λ)^2 - 4 = λ^2 - 4λ = 0解上述方程得到特征值λ = 0, 4。
数学论文二元函数极值的求解方法证:不妨设),(),(00y x y x f z 在点=处有极大值,),(00y x 则对于的某邻域内任何),,(),(00y x y x ≠都有),(),(00y x f y x f <,故当时00,x x y y ≠=,有),,(),(000y x f y x f <则一元函数00),(x x y x f =在处有极大值,必有;0),(00=y x f x 类似地,可证.0),(00=y x f y对于二元函数甚至多元函数与一元函数的情形类似,凡是能使一阶偏导数同时为零的点可以称为函数的驻点。
备注:具有偏导数的极值点必然是驻点,但驻点不一定是极值点。
2、二元函数极值充分条件为了讨论二元函数f 在点),(000y x p 取得极值的充分条件,我们假定f 具有二阶连续偏导数,并记)()()()()(00000p xx xx xx xx yy yx xy xx f f f f f p f p f p f p f p H ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡= 他称为f 在),(000y x p 的黑赛矩阵。
定理2.1(极值充分条件)设函数),(y x f z =在点),(00y x 的某邻域内连续且有直到二阶的连续偏导数,又,0),(00=y x f x .0),(00=y x f y令.),(,),(,),(000000C y x f B y x f A y x f yy xy xx ===则),(y x f 在),(00y x 处是否取得极值的条件如下:(1)、当02>-B AC 时,函数),(y x f 在),(00y x 处有极值,且当0>A 时有极小值),(00y x f ;0<A 时有极大值),(00y x f ;(2)、当02<-B AC 时,函数),(y x f 在),(00y x 处没有极值;(3)、当02=-B AC 时,函数),(y x f 在),(00y x 处可能有极值,也可能没有极值。
二元函数开区域内唯一极值点极值点是函数在某个区域内取得的最大值或最小值。
在二元函数中,我们可以通过求偏导数来找到极值点。
偏导数是多元函数在某个变量上求导时将其他变量视为常数的导数。
假设有一个二元函数f(x,y),我们想要找到它在开区域D内的极值点。
首先,我们需要找到函数的偏导数f_x和f_y。
然后,我们需要解方程组f_x=0和f_y=0,求得极值点的候选值。
然而,这些候选值并不一定都是极值点。
为了确定哪些是真正的极值点,我们需要进一步进行判断。
一种方法是计算二阶偏导数,即求f_xx、f_xy和f_yy。
然后,我们可以利用二阶导数的符号来判断极值点的性质。
如果f_xx>0,且f_xy*f_xx-f_yy*f_xx>0,那么该点为极小值点;如果f_xx<0,且f_xy*f_xx-f_yy*f_xx>0,那么该点为极大值点。
如果f_xy*f_xx-f_yy*f_xx<0,则该点既不是极小值点也不是极大值点。
需要注意的是,以上的判断条件只适用于开区域内的极值点。
在闭区间的情况下,我们还需要考虑边界点和函数在边界上的取值情况。
这是因为在边界上,函数可能会取得更大或更小的值,而不是在内部取得极值。
我们还可以利用二元函数的图像来直观地判断极值点。
通过观察函数的等高线图或者三维图像,我们可以找到极值点所在的位置。
然而,这种方法只适用于简单的函数,对于复杂的函数往往不太实用。
总结一下,二元函数开区域内的极值点是通过求偏导数和解方程组来确定的。
然后,我们可以利用二阶偏导数的符号来判断极值点的性质。
此外,我们还可以通过观察函数的图像来找到极值点的位置。
极值点在数学和实际问题中都具有重要的意义。
它们可以帮助我们优化函数,找到最优解。
在经济学、物理学和工程学等领域,极值点的概念被广泛应用。
希望通过本文的介绍,读者对二元函数的极值点有了更深入的了解,能够更好地应用于实际问题中。
二元函数判断极值点的方法二元函数是含有两个自变量的函数,通常表示为f(x,y)。
判断二元函数的极值点是求解该函数的局部最大值或最小值的位置。
在数学中,存在多种方法来判断二元函数的极值点,下面将介绍其中一些常用的方法。
1. 偏导数法:使用偏导数来确定极值点是最常见和常用的方法之一。
首先,计算函数f(x,y)分别对x和y的偏导数,记为f/x和f/y。
然后,求解方程组f/x = 0和f/y = 0,得到极值点的可能位置。
最后,使用二阶偏导数的符号(即Hessian矩阵)来确定这些可能位置是极大值点、极小值点还是鞍点。
2. 二次型法:对于二元函数f(x,y),可以构建二次型Q(x,y) =f_xx(x,y) + 2f_xy(x,y) + f_yy(x,y),其中f_xx,f_xy和f_yy分别代表二阶偏导数。
通过对二次型进行特征值分析,可以判断极值点的性质。
如果二次型的所有特征值都为正,则该点为极小值点;如果所有特征值都为负,则该点为极大值点;如果特征值有正有负,则该点为鞍点。
3. Lagrange乘数法:当二元函数f(x,y)在一定约束条件下求取极值时,可以使用Lagrange乘数法。
该方法通过引入拉格朗日乘数λ来将约束条件纳入考虑,将问题转化为无约束的极值问题。
具体步骤为:首先构建拉格朗日函数L(x,y,λ) = f(x,y) + λg(x,y),其中g(x,y)为约束条件;然后求解L的偏导数关于x、y和λ的方程组,并解得极值点。
4. 格雷默法则:对于二元函数f(x,y),如果在某个点(x0,y0)的某个邻域内,所有偏导数f/x和f/y的值都存在且连续,且满足f/x ≠0或f/y ≠ 0,那么点(x0,y0)是二元函数的一个极值点。
在实际应用中,以上方法可以根据具体问题的需求选择合适的方法来判断二元函数的极值点。
同时,这些方法也可以用于更高维度的函数的极值判断。
二元函数的极值与最值在数学中,二元函数是一个带有两个自变量的函数,通常表示为f(x, y),其中x和y分别是独立变量。
当我们定义一个函数时,我们通常希望找到函数的最大和最小值等重要信息。
在这篇文章中,我们将探讨二元函数的极值点和最值点,以及如何找到它们。
极值和最值的概念首先,我们需要了解的是“极值”和“最值”的概念。
在微积分中,极值是指在一个函数曲线上的局部最大值或最小值。
具体地说,一个函数在一个点上的导数为零,这个点就是函数的驻点。
如果该点是一个局部最大值或最小值,则它是该函数的一个极值点。
最值是在函数的定义域内找到的最大值或最小值。
二元函数的极值点要找到二元函数的极值点,我们需要找到函数曲面上的局部最大值或最小值。
这意味着我们需要找到函数曲面上的所有可能的驻点。
与一元函数类似,我们可以使用偏导数来找到驻点。
因此,对于二元函数f(x, y),我们可以用以下公式来计算它的偏导数:∂f/∂x = 0 和∂f/∂y = 0这些方程可以帮助我们找到一个或多个可能的驻点。
然而,这些驻点可能是最大值或者最小值,或者它们根本不是。
我们还需要使用二阶偏导数来确定驻点的角色。
如果二阶偏导数是:1. 正的,那么这个点是局部最小值点。
2. 负的,那么这个点是局部最大值点。
3. 0,那么这个点不是极点。
最终,我们将找到所有可能的极值点,以及它们的角色和函数值。
二元函数的最值点要找到二元函数的最大值和最小值,我们要按照以下步骤进行:1. 找到函数曲面上的所有极值点2. 在函数的定义域内找到函数曲面上的所有最大值和最小值。
3. 在找到的所有值中找到全局最大值和最小值。
在这个过程中,我们需要使用一些数学方法来找到最大值和最小值。
最常见的方法是使用拉格朗日乘数法。
拉格朗日乘数法拉格朗日乘数法是一种用于最值问题的数学方法。
这个方法的基本思想是,如果一个函数f(x, y)在限制条件g(x, y)下取得最大值或最小值,那么这个点的梯度向量(∇f)和限制条件的梯度向量(∇g)之间应该是平行的。
二元函数用海塞矩阵判断极值
在多元函数中,当我们要判断一个函数的极值时,需要使用海塞矩阵来进行判断。
而对于二元函数,海塞矩阵的形式就是:
H(f)(x,y)=[f_{xx}(x,y) f_{xy}(x,y)]
[f_{xy}(x,y) f_{yy}(x,y)]
其中 f_{xx}, f_{xy}, f_{yy} 分别为二阶偏导数。
使用海塞矩阵来判断二元函数的极值,需要以下步骤:
1. 求出海塞矩阵 H(f)(x,y)
2. 计算海塞矩阵的行列式 D = f_{xx}(x,y) * f_{yy}(x,y) - [f_{xy}(x,y)]^2
3. 当 D > 0 且 f_{xx}(x,y) > 0 时,函数 f(x,y) 在点 (x,y) 处有一个局部极小值。
4. 当 D > 0 且 f_{xx}(x,y) < 0 时,函数 f(x,y) 在点 (x,y) 处有一个局部极大值。
5. 当 D < 0 时,函数 f(x,y) 在点 (x,y) 处没有极值。
6. 当 D = 0 时,无法判断是否有极值,需要结合其他方法来判断。
通过以上步骤,我们可以使用海塞矩阵来判断二元函数的极值。
这对于优化问题和最优化问题的解决非常有帮助。
- 1 -。
摘要本文主要讨论了二元函数的极值问题,不仅介绍了二元函数极值方面的有关概念和定理,还给出了这些定理的证明,并举出了二元函数极值方面的几个理论问题,特别地对极值判别式进行了推广和求解条件极值的拉格朗日乘数法进行了一般化改进.本文以高教版数学分析教材为出发点,在讨论的过程中重温了书本上的定理,更对书中的定理进行升华,使定理能够更好解决实际问题,进而运用的更加广泛.关键词:二元函数;极大值;极小值AbstractThe extremum of function of two variables is expounded in this thesis. Not only are some relevant ideas and definitions are presented in this thesis, but also the relative proof to them. Furthermore, it exhibits several theoretical problems of the extremum of function of two variables as well. Particularly, it expands the discriminant of the extremum and generally improves Lagrangian Multiplier that is to find a minimum or a maximum of a function. On one hand, based on the teaching material of Advanced Mathematics, the thesis reviews the definitions in the textbook throughout the procedure of specification. On the other hand, it sublimates these definitions so that we can solve the practical issues better and use them more widely.Key words:function of two variables;maximun value; minimum value摘要 (I)Abstract ................................................................... I I 目录 ...................................................................... I II 1引言.. (1)2二元函数极值问题的相关概念 (1)2.1二元函数定义 (1)2.2二元函数及其极大极小值的定义 (2)3二元函数的极值问题 (2)3.1二元函数极值存在的必要条件 (2)3.2二元函数极值存在的充分条件 (3)3.3求二元函数极值的步骤 (5)4特殊情况下二元函数极值 (6)5条件极值问题 (8)5.1代入法 (9)5.2拉格朗日(Lagrange)乘数法 (9)6总结 (13)参考文献 (14)函数极值问题是一个非常普通的数学问题,是经典微积分学最成功的应用,不仅在实际问题中占有重要地位,而且也是函数性态的一个重要特征.在一元函数中,可以利用函数的导数求得函数的极值,从而进一步解决一些有关最大,最小值应用问题.同样利用偏导数,也可以解决二元函数的极值问题.2二元函数极值问题的相关概念2.1二元函数定义定义 1 设平面点集D 包含于2R ,若按照某对应法则f ,D 中每一点),(y x P 都有唯一确定的实数z 与之对应,则称f 为在D 上的二元函数.记作,D :R f → (1) 且称D 为f 的定义域;P 对应的z 为f 在点P 的函数值,记作),(y x f z =或)(P f z =;全体函数值的集合称为f 的值域,记作R f ⊂(D).通常还把P 的坐标x 与y 称为自变量,而把z 称为因变量.当把D y x ∈),(和它所有的函数值),(y x f z =一起组成三维数据组()z y x ,,时,三维欧氏空间3R 中的点集}{3)y ,(),,(|),,(R D x y x f z z y x S ⊂∈==便是二元函数f 的图像.通常),(y x f z =的图象是一空间曲面,f 的定义域D 便是该曲面在xOy 平面上的投影.为了方便起见,我们把(1)式所确定的二元函数也记作),(y x f z =, D y x ∈),(,或 )(P f z =,D P ∈,且当它的定义域D 不会被误解的情况下,也简单的说“函数),(y x f z =”或“函数f ”.2.2二元函数及其极大极小值的定义定义 2 设函数f 在点),(000y x P 的某领域)(0P U 内有定义,若对于任何点)(),(0P U y x P ∈,成立不等式)()(0P f P f ≥(或)()(0P f P f ≤),则称函数f 是在点0P 取得极小值(或极大值),点0P 称为f 的极小(极大)值点.极大值、极小值统称极值,极大值点、极小值点统称极值点.注意:这里所讨论的极值点只限于定义域的内点.例如,设2223),(y x y x f +=,221),(y x y x g --=,xy y x h 2),(=.由定义直接知道,坐标原点)0,0(是f 的极小值点,是g 的极大值点,但不是h 的极值点.这是因为对于任何点),(y x ,恒有0)0,0(),(=≥f y x f ;对任意{}1y x |x,y x,y 22≤+∈)()(,恒有1)0,0(),(=≤g y x g ;而对于函数h ,在原点的任意小邻域内,既含有使0),(>y x h 的第一、三象限中的点,又含有使0),(<y x h 的第二、四象限中的点,所以0)0,0(=h 既不是极大值又不是极小值.由定义可见,若f 在点),(00y x 取得极值,刚当固定0y y =时,一元函数),(0y x f 必定在0x x =取得相同的极值.同理,一元函数),(0y x f 必定在0y y =也取得相同的极值. 那么一般情况下如何求二元函数的极值呢?仿照一元函数的极值的讨论,我们得到二元函数极值存在的必要条件如下.3二元函数的极值问题3.1二元函数极值存在的必要条件定理 1 若函数f 在点),(000y x P 处存在偏导数,且函数在该点取得极值,则有0),(),(0000==y x f y x f y x .证明 因为点),(00y x 是函数),(y x f 的极值点,若固定),(y x f 中的变量0y y =,则),(0y x f z =是一个一元函数且在0x x =处取得极值,由一元函数极值的必要条件知0),(00=y x f x ,同理有0),(00=y x f y .反之,凡是满足方程组⎩⎨⎧==0),(0),(y x f y x f y x 的点),(00y x 称为函数),(y x f z =的驻点.定理说明,只要函数),(y x f z =的两个偏导数存在,那么它的极值点一定是驻点,反过来,驻点是不是一定为极值点呢?例如,函数22y x z +-=,在点()0,0处的两个偏导数为0,即()0,0是驻点,但在()0,0的任一邻域内函数既有正值也有负值,所以()0,0不是极值点,即驻点不一定是极值点.另外,极值点也可能是偏导数不存在的点.比如,上半锥面22y x z +=在点()0,0的偏导数不存在,但()0,0是函数的极小值点,函数极小值为0.3.2二元函数极值存在的充分条件判断二元函数),(y x f 在),(000y x P 取得极值的充分条件,我们假定函数f 有二阶连续偏导数,并记0f p =⎢⎣⎡)()(00P f P f yx xx ⎥⎥⎦⎤)()(00xy P f P f yy =⎢⎣⎡yx xx f f 0xy P yy f f ⎥⎥⎦⎤, 称它为f 在),(000y x P 的黑塞矩阵.定义3 若函数f 在点),(000y x P 的某邻域)(0P U 具有直到1+n 阶的连续偏导数,则对)(0P U 内任一点),(00k y h x ++,存在相应的)1,0(∈θ,使得).,()()!1(1),()(!1),()(!21),()(),(),(00100002000000k y h x f y k x h n y x f yk x h n y x f y k x h y x f yk x h y x f k y h x f n n θθ++∂∂+∂∂++∂∂+∂∂+⋯+∂∂+∂∂+∂∂+∂∂+=+++ (2)式称为二元函数f 在点0P 的泰勒公式,其中i m i i m i mm i i m m k h y x f y x C y x f y k x h --=∂∂∂=∂∂+∂∂∑),(),()(00000. 定理2 (极值充分条件)设二元函数f 在点),(000y x P 的某邻域)(0P U 具有二阶连续偏(2)导数,且0P 为f 的稳定点,则当)(0P H f 为正定矩阵时,此函数f 在0P 有极小值;当)(0P H f 为负定矩阵时,在0P 有极大值;当)(0P H f 为不定矩阵时,在0P 不取极值. 证明 由f 在0P 的二阶泰勒公式,并注意到条件0)()(00==P f P f y x ,有)(),)((),(21),(),(22000y x y x P H y x y x f y x f T f ∆+∆ο+∆∆∆∆=-. 由于)(0P H f 正定,所以对任何)0,0(),(≠∆∆y x 恒使二次型0),)((),(),(0>∆∆∆∆=∆∆T f y x P H y x y x Q .因此存在一个与y x ∆∆,无关的正数q ,使得)(2),(22y x q y x Q ∆+∆≥∆∆.则对于充分小的0()U P 只要),(y x ∈0()U P ,就有0))1()(,()(),(),(),(22222200≥ο+∆∆=∆+∆ο+∆∆≥-q y x y x y x q y x f y x f ,即f 在),(000y x P 取极小值.同理可证)(0P H f 为负定矩阵时,f 在),(000y x P 取极大值.最后,当)(0P H f 不定时,f 在0P 不取极值.假设f 取极值(因为不失一般性,所以我们不妨设为取极大值),对任何过0P 的直线x t x x ∆+=0,y t y y ∆+=0,)(),(),(00t y t y x t x f y x f φ=∆+∆+=在0t 也取极大值.由一元函数取极值的充分条件,0)0(>''φ是不可能的(否则φ在0t 将取极小值),故0)0(≤''φ.而又有 y x yf xf t ∆+∆=φ')(,22)(2)()(y f yf x x f t yy xy xx ∆+∆∆+∆=φ'',T f y x P H y x ),)((),()0(0∆∆∆∆=''φ,这表明)(0P H f 为负半定的.同理,f 倘若取极小值,则将导致)(0P H f 为正半定.也就是说,当f 在0P 取极值时,)(0P H f 必须是正半定或负半定,但这与)(0P H f 不定相矛盾.证毕.若函数f 如定理2所设,设0P 是f 的稳定点,则我们可以将定理2写成如下比较实用的形式:①当0)(0>P f xx ,0))((02>-P f f f xy yy xx 时,f 在点0P 取得极小值; ②当0)(0<P f xx ,0))((02>-P f f f xy yy xx 时,f 在点0P 取得极大值; ③当0))((02<-P f f f xy yy xx 时,f 在点0P 不能取得极值;④当0))((02=-P f f f xy yy xx 时,不能肯定f 在点0P 是否取得极值.3.3求二元函数极值的步骤第一步,首先求出偏导数x f ,y f ,xx f ,yy f ,xy f ;第二步,然后解方程组⎩⎨⎧==00yx f f 求出驻点P ;第三步,求出二元函数在驻点P 处)(P f xx 、)(P f yy 、)(P f xy 的值及))((2P f f f xy yy xx -的符号,再根据定理2判定出极值点;第四步,求出二元函数的极大值或者极小值.例1 求),(y x f y x y xy x +-+-222的极值点.解 由方程组 ⎩⎨⎧=+-==--=012022x y f y x f yx 得f 的稳定点为)0,1(0P ,由于02)(0>=P f xx ,2)(0=P f yy ,1)(0-=P f xy ,03))((02>=-P f f f xy yy xx ,故f 在0P 取极小值1)0,1(-=f .又因为f 处处可微,所以0P 为f 的惟一极值点.例2 求xy y x z 333-+=的极值.解 由方程组⎪⎩⎪⎨⎧=-==-=03303322x y f y x f y x 得f 的稳定点为)1,1(1P 、)0,0(2P ,由于x f xx 6=、y f yy 6=、3-=xy f ,所以027))((12>=-P f f f xy yy xx .故f 在1P 取极小值1)1,1(-=f .又因为 09))((22<-=-P f f f xy yy xx ,所以2P 不是f 的极值点.例3 讨论),(y x f =62+-xy y 是否存在极值点.解 由方程组 ⎩⎨⎧=-==-=020x y f y f yx 得稳定点为原点)0,0(0P .又01))((02<-=-P f f f xy yy xx ,故原点不是f 的极值点.又因为f 在定义域内处处存在偏导数,所以f 没有极值点.例4 讨论)2)((),(22y x y x y x f --=在原点是否取得极值.解 容易验证原点为其稳定点,但在原点02=-xy yy xx f f f ,所以无法判定f 在原点是否取得极值.但是,我们又很容易发现,当222y x y <<时,),(y x f 0;当22y x >或2y x <时,),(y x f 0.所以函数f 不可能在原点取得极值.4特殊情况下二元函数极值对于一个二元函数来说,当),(000y x P 为稳定点,判别式0))((02≠-=P f f f M xy yy xx 时,可以判定f 在点0P 取得极小值、极大值或不能取得极值.但是,在判别式为零的时候,就没有肯定的答案了,下面我们就来讨论一下判别式为零时的情形.根据极值的定义可知,要判定),(000y x P 是否为极值点,只要判定),(y x P 在),(000y x P 的某邻域0()U P 内变化时,),(),(00y x f y x f f -=∆是否保持定号,并由此来判断.假设f 的所有二阶偏导数连续,则可以利用泰勒公式来讨论f ∆的符号.定理3 设点),(000y x P 是二元函数),(y x f 的稳定点,0===xy yy xx f f f ,若),(y x f 在0P 的某邻域内具有三阶连续偏导数,且至少有一个不为零时,则f 在0P 无极值.证明 由所给的泰勒展开式有),(),(][61),(),(3300300y x y x f yf k x f h y x f y x f ∆+∆ο+∂∂-∂∂=- 其中00,y y k x x h -=-=,而)(33y x ∆+∆ο为当),(),(00y x y x →时f 的无穷小量.所以,对于0P 的充分小的邻域0()U P ,只要当)(),(0P U y x ∈时,就能保证),(][61003y x f yf k x f h ∂∂-∂∂与),(),(00y x f y x f - 同号.这是因为),(][61003y x f yf k x f h ∂∂-∂∂ ⎪⎪⎭⎫ ⎝⎛∂∂+∂∂∂+∂∂∂+∂∂=30033200322003230033),(),(3),(3),(61y y x f k y x y x f hk y x y x f k h x y x f h , 若),(y x f 在0P 的某邻域内三阶连续偏导数至少有一个不为零,即0),(),(),(),(23003220032200323003≠⎥⎦⎤⎢⎣⎡∂∂+⎥⎦⎤⎢⎣⎡∂∂∂+⎥⎦⎤⎢⎣⎡∂∂∂+⎥⎦⎤⎢⎣⎡∂∂y y x f y x y x f y x y x f x y x f , 我们来分情况讨论1若0)(033≠∂∂P xf 时,取00,y y x x h =-=,则 当0x x >时,0>h 则03>h ;当0x x <时,0<h 则30h ; 从而)(0333P x f h ∂∂的符号是不确定的.即当0)(033≠∂∂P xf 时,f 在0P 无极值. 2若0)(033≠∂∂P yf 时,取00,y y k x x -==,同理可得f 在0P 无极值.3若0)(033=∂∂P x f ,0)(033=∂∂P y f ,则0)(023≠∂∂∂P y x f ,或0)(023≠∂∂∂P yx f.不妨设0)(023≠∂∂∂P yx f,此时 ]),(),([21),(),(2003200300y x y x f k y x y x f h y x f y x f ∂∂∂+∂∂∂=-,取0>k 充分小,使得20032003),(),(yx y x f k y x y x f h ∂∂∂>∂∂∂,则),(),(00y x f y x f -的符号是由yx y x f k h ∂∂∂20032),(决定.从而k 取正负号时导致),(),(00y x f y x f -在),(00y x 的任意小邻域可取正可取负.因此,),(),(00y x f y x f -的符号不确定.即当0)(033=∂∂P x f ,0)(033=∂∂P yf,而0)(023≠∂∂∂P y x f 时,f 在0P 无极值.在0)(023≠∂∂∂P yx f时,同理可得f 在0P 无极值. 综上,定理得证.例5 讨论函数323532),(y xy x y x f +-=在原点是否有极值.解 函数),(y x f 在原点处的一,二阶偏导数0=====yy xy xx y x f f f f f ,而0123≠=x f ,由定理3可得,函数),(y x f 在原点不取极值.5条件极值问题在大量二元函数取极值的问题中,有一类问题是经常碰到的,即所谓求函数“条件极值”的问题.例如,要设计一个容量为V 的长方形开口容器,那么,当容器的长,宽,高各等于多少时,其表面积最小?为了解决上面这个问题,我们不妨设容器的长、宽、高分别为c b a 、、,则该容器表的面积为ac bc ab c b a S 22),,(++=.由此不难看出,上述表面积函数S 的自变量c b a 、、,不仅要符合定义域的要求0,0,0>>>c b a ,而且还须满足条件abc V =.像上面这类附有约束条件的极值问题,称为条件极值问题(不带约束条件的极值问题不妨称为无条件极值问题).一般地,求二元函数的条件极值,在讨论二元函数),(y x f z =在约束条件0),(=y x g 下的极值问题时,我们主要使用下面两个方法.5.1代入法在约束条件0),(=y x g 中,如果能解x (或y ), 即)(y x ϕ=(或)(x y ϕ=),将它代入),(y x f z =中,那么)),((y y f z ϕ=(或))(,(x x f z ϕ=),这样就把二元函数),(y x f z =在约束条件0),(=y x g 下的极值问题,转化为求一元函数)),((y y f z ϕ=(或))(,(x x f z ϕ=)的极值问题了,而一元函数的极值问题已经在微积分中得到圆满解决.例5 求xy z =在约束条件1=+y x 的极值.解 由约束条件x y -=1代入z 中,得到2)1(x x x x z -=-=,令021x =-='x z ,解得21=x , 又因为02xx<-=''z ,所以21=x 为极大值点. 故函数z 的极大值为41)21,21(=z .5.2拉格朗日(Lagrange)乘数法在某些情况下,要想在约束条件0),(=y x g 中解出x (或y )不总是可能的,下面我们介绍一种不直接依赖消元而求解条件极值问题的有效方法:(1)引入辅助变量λ和辅助函数),(),(),,(y x g y x f y x L λλ+=;(2)求出),,(λy x L 对λ,,y x 的一阶偏导数,并令它们都为零,然后联立组成方程组即:⎪⎩⎪⎨⎧===+==+=0),(),,(0),(),(),,(0),(),(),,(y x g y x L y x g y x f y x L y x g y x f y x L y y y x x x λλλλλλ 解上面这个方程组,得出解),(i i y x )2,1(⋯⋯=i ,都是),(y x f z =在约束条件0),(=y x g 下的驻点,这是因为由(3)和(4)得),(),(),(),(y x g y x f y x g y x f yy x x '-=''-='λλ由(6)和(7)得(3) (4) (5)(6)(7)0),(),(),(),(='''-'y x g y x g y x f y x f y x y x 再由(5)得0),(),(=''+'x y x y y x g y x g所以有),(),(y x g y x g y y x x ''-=' 于是0),(),(=''+'x y x y y x f y x f这样我们就容易得到0),(),(=''+'='x y x x y y x f y x f z所以说),(i i y x )2,1(⋯⋯=i 都是),(y x f z =在约束条件0),(=y x g 下的驻点.这里需要说明一点,如果在实际问题中,能判定函数),(y x f z =在约束条件0),(=y x g 下只有一个极大值或极小值,并且上面的方程组也只有惟一的解),(00y x ,那么点),(00y x 就是极大值或极小值.当然,在不能判定的情况下,我们还要继续下面的步骤;(3)为了判断),(i i y x )2,1(⋯⋯=i 是否是极值点,我们设),(y x f z =有连续的一阶、二阶偏导数,y 对x 的一阶、二阶导数存在,那么xx y x x yy yx xy xx xx y y x f y y y x f y x f y x f y x f z '''+''''+''+''+''=''),(]),(),(),([),(由一元函数极值的第二判别法得①当0),(<''i i xx y x z 时,),(y x f z =在约束条件0),(=y x g 下有极大值),(i i y x f z =; ②当0),(>''i i xx y x z 时,),(y x f z =在约束条件0),(=y x g 下有极小值),(i i y x f z =.上面这种方法就是拉格朗日乘数法,辅助函数L 称为拉格朗日函数,辅助变量λ称为拉格朗日乘数.这个方法虽然看起来很烦琐,但是它很好的解决了代入法的不足之处,在解决二元函数条件极值问题方面应用非常广泛.现在我们就用拉格朗日乘数法来重新求xy z =在约束条件1=+y x 的极值.引入辅助变量λ和辅助函数)1(),(),(),,(-++=+=y x xy y x g y x f y x L λλλ;然后求出),,(λy x L 对λ,,y x 的一阶偏导数,并令它们都为零组成方程组,即⎪⎩⎪⎨⎧=-+=+==+=010),,(0),,(y y x x y x L y y x L x λλλλ 解方程组得唯一驻点)21,21(,由于当±∞→x 时,∞→ y ,故-∞→=xy z ,则函数z 必在此处取得极大值41)21,21(=z .当然,我们还可以用步骤三去判断)21,21(是否是极值点.很容易求得y y x f x ='),(、x y x f y ='),(、0),(=''y x f xx、1),(),(=''=''y x f y x f yx xy 、0),(=''y x f yy 、1-='x y 、0=''xx y ,所以,02),(]),(),(),([),()21,21(<-='''+''''+''+''+''=''xx y x x yy yx xy xx xx y y x f y y y x f y x f y x f y x f z , 故xy z =在点)21,21(取得极大值41)21,21(=z .例6 求函数y x y x f z +==),(在条件222=+y x 下的极值.解 引入辅助变量λ和辅助函数)2(),,(22-+++=y x y x y x L λλ求出),,(λy x L 对λ,,y x 的一阶偏导数,并令它们都为零组成方程组,即⎪⎩⎪⎨⎧=+=+==+=2021),,(021),,(22y x y y x L x y x L y x λλλλ 解方程组得到两个驻点()11,和()11--,.又有, 1),(),(='='y x f y x f y x ,0),(),(=''=''y x f y x f yy xx,0),(),(=''=''y x f y x f yx xy ,yxy x -=',3322222yy x y y yx x y yy x y y xxx -=+-=+-='--='',所以, 02),(]),(),(),([),()1,1(<-='''+''''+''+''+''=''xx y x x yy yx xy xx xx y y x f y y y x f y x f y x f y x f z那么,函数),(y x f z =在点()11,取得极大值2)1,1(=z ; 又因为02),(]),(),(),([),()1,1(>='''+''''+''+''+''=--''xx y x x yy yx xy xx xx y y x f y y y x f y x f y x f y x f z那么,函数),(y x f z =在点()11--,取得极小值2)1,1(-=--z .例7 求函数22),(y x y x f z +==在条件04=-+y x 下的极值.解: 引入辅助变量λ和辅助函数)1(),,(22-+++=y x y x y x L λλ求出),,(λy x L 对λ,,y x 的一阶偏导数,并令它们都为零组成方程组即:⎪⎩⎪⎨⎧=-+=+==+=0402),,(02),,(y x y y x L x y x L y x λλλλ 解方程组得到惟一的驻点)2,2(.又有x y x f x 2),(=',y y x f y 2),(=',2),(=''y x f xx ,0),(),(=''=''y x f y x f yx xy ,2),(=''y x f yy ,1-='x y ,0=''xx y ,所以,04),(]),(),(),([),()2,2(>='''+''''+''+''+''=''xx y x x yy yx xy xx xx y y x f y y y x f y x f y x f y x f z那么,函数),(y x f z =在点)2,2(取得极大值8)2,2(=xx z .6总结本文主要讨论数学分析中二元函数的极值问题.把一元函数的极值问题推广到多元函数的情形,得到了一些新的结果,并给出了一些未推广前不能求解,而利用推广后的结论可以求解的例子.本文先证明稳定点为极值点的充分条件,并给出其判别式,再分析判别式为零的情形,来解决与此相关的数学问题.参考文献[1] 华东师范大学数学系.数学分析(下册 第三版)[M].北京:高等教育出版社,2003. [2] 刘玉琏等.数学分析讲义(下册 第四版)[M].北京:高等教育出版社,2003. [3]万淑香.二元函数的极值问题[J].鸡西大学学报,2007,4:75-76.[4]柴文祥等. 二元函数极值判别的一点注记[J].牡丹江师范学院学报,2011,4:3-4 [5]刘连褔.02=-=∆AC B 时二元函数极值问题讨论[J]. 廊坊师范学院学报,2010,10:16-17.[6]刘晓俊. 二元函数求条件极值的方法[J]. 金融教学与研究,1994,3:57-59.。