2D-FFT及IFFT(C语言实现(转载)

FFT实现的C语言代码（转载）-（基2FFT及IFFT算法C语言实现）FFT实现的C语言代码- -（基2FFT及IFFT算法C语言实现）Given two images A and B, use image B to cover image A. Where would we put B on A, so that the overlapping part of A and B has the most likelihood? To simplify the problem, we assume that A and B only contain numbers between 0 and 255. The difference between A and B is defined as the square sum of the differences of corresponding elements in the overlapped parts of A and B.For example, we haveA (3 * 3): a1 a2 a3B (2 * 2): b1 b2a4 a5 a6 b4 b5a7 a8 a9When B is placed on position a5, the difference of them is ((b1-a5)^2 + (b2-a6)^2 + (b4-a8)^2 + (b5-a9)^2). Now we hope to have the position of the top left corner of B that gives the minimum difference. (B must completely reside on A) It is clear that a simple solution will appear with very low efficiency when A and B have too many elements. But we can use 1-dimensional repeat convolution, which can be computed by Fast Fourier Transform (FFT), to improve the performance.A program with explanation of FFT is given below:/*** Given two sequences {a1, a2, a3.. an} and {b1, b2, b3... bn}, * their repeat convolution means:* r1 = a1*b1 + a2*b2 + a3*b3 + ... + an*bn* r2 = a1*bn + a2*b1 + a3*b2 + ... + an*bn-1* r3 = a1*bn-1 + a2*bn + a3*b1 + ... + an*bn-2* ...* rn = a1*b2 + a2*b3 + a3*b4 + ... + an-1*bn + an*b1* Notice n >= 2 and n must be power of 2.*/#include#include#include#define for if (0); else forusing namespace std;const int MaxFastBits = 16;int **gFFTBitTable = 0;int NumberOfBitsNeeded(int PowerOfTwo) {for (int i = 0;; ++i) {if (PowerOfTwo & (1 << i)) {return i;}}}int ReverseBits(int index, int NumBits) {int ret = 0;for (int i = 0; i < NumBits; ++i, index >>= 1) {ret = (ret << 1) | (index & 1);}return ret;}void InitFFT() {gFFTBitTable = new int *[MaxFastBits];for (int i = 1, length = 2; i <= MaxFastBits; ++i, length <<= 1) {gFFTBitTable[i - 1] = new int[length];for (int j = 0; j < length; ++j) {gFFTBitTable[i - 1][j] = ReverseBits(j, i);}}}inline int FastReverseBits(int i, int NumBits) {return NumBits <= MaxFastBits ? gFFTBitTable[NumBits - 1][i] : ReverseBits(i, NumBits);}void FFT(bool InverseTransform, vector >& In, vector >& Out) {if (!gFFTBitTable) { InitFFT(); }// simultaneous data copy and bit-reversal ordering into outputsint NumSamples = In.size();int NumBits = NumberOfBitsNeeded(NumSamples);for (int i = 0; i < NumSamples; ++i) {Out[FastReverseBits(i, NumBits)] = In[i];}// the FFT processdouble angle_numerator = acos(-1.) * (InverseTransform ? -2 : 2);for (int BlockEnd = 1, BlockSize = 2; BlockSize <= NumSamples; BlockSize <<= 1) {double delta_angle = angle_numerator / BlockSize;double sin1 = sin(-delta_angle);double cos1 = cos(-delta_angle);double sin2 = sin(-delta_angle * 2);double cos2 = cos(-delta_angle * 2);for (int i = 0; i < NumSamples; i += BlockSize) {complex a1(cos1, sin1), a2(cos2, sin2);for (int j = i, n = 0; n < BlockEnd; ++j, ++n) {complex a0(2 * cos1 * a1.real() - a2.real(), 2 * cos1 * a1.imag() - a2.imag());a2 = a1;a1 = a0;complex a = a0 * Out[j + BlockEnd];Out[j + BlockEnd] = Out[j] - a;Out[j] += a;}}BlockEnd = BlockSize;}// normalize if inverse transformif (InverseTransform) {for (int i = 0; i < NumSamples; ++i) {Out[i] /= NumSamples;}}}vector convolution(vector a, vector b) {int n = a.size();vector > s(n), d1(n), d2(n), y(n);for (int i = 0; i < n; ++i) {s[i] = complex(a[i], 0);}FFT(false, s, d1);s[0] = complex(b[0], 0);for (int i = 1; i < n; ++i) {s[i] = complex(b[n - i], 0);}FFT(false, s, d2);for (int i = 0; i < n; ++i) {y[i] = d1[i] * d2[i];}FFT(true, y, s);vector ret(n);for (int i = 0; i < n; ++i) {ret[i] = s[i].real();}return ret;}int main() {double a[4] = {1, 2, 3, 4}, b[4] = {1, 2, 3, 4};vector r = convolution(vector(a, a + 4), vector(b, b + 4));// r[0] = 30 (1*1 + 2*2 + 3*3 + 4*4)// r[1] = 24 (1*4 + 2*1 + 3*2 + 4*3)// r[2] = 22 (1*3 + 2*4 + 3*1 + 4*2)// r[3] = 24 (1*2 + 2*3 + 3*4 + 4*1)return 0;}InputThe first line contains n (1 <= n <= 10), the number of test cases.For each test case, the first line contains four integers m, n, p and q, where A is a matrix of m * n, B is a matrix of p * q (2 <= m, n, p, q <= 500, m >= p, n >= q). The following m lines are the elements of A and p lines are the elements of B.OutputFor each case, print the position that gives the minimum difference (the top left corner of A is (1, 1)). You can assume that each test case has a unique solution.Sample Input22 2 2 21 23 42 31 43 3 2 20 5 50 5 50 0 05 55 5Sample Output1 11 2Author:DU, Peng。

FFT及IFFTC语言实现FFT（快速傅里叶变换）和IFFT（快速傅里叶逆变换）是傅里叶变换在计算机科学和信号处理中的高效实现方法。

它们广泛应用于图像处理、音频处理、通信系统等领域。

下面将详细介绍FFT和IFFT的C语言实现。

首先，让我们了解一下DFT（离散傅里叶变换）。

DFT将一个离散的时间域序列转换为离散的频域序列，其定义如下：其中，N表示序列的长度，x(n)是输入序列，X(k)是输出序列。

FFT是DFT的一种高效实现方法，它利用了序列的对称性质，将操作的复杂度从O(N^2)降低到O(NlogN)。

IFFT则是FFT的逆过程，可以将频域序列恢复为时间域序列。

以下是FFT的C语言实现代码：```c#include <stdio.h>#include <math.h>typedef structdouble real;double imag;result.real = a.real * b.real - a.imag * b.imag;result.imag = a.real * b.imag + a.imag * b.real;return result;result.real = a.real + b.real; result.imag = a.imag + b.imag; return result;result.real = a.real - b.real; result.imag = a.imag - b.imag; return result;if (N <= 1)return;}for (int i = 0; i < N / 2; i++) even[i] = x[2 * i];odd[i] = x[2 * i + 1];}fft(even, N / 2);fft(odd, N / 2);for (int k = 0; k < N / 2; k++)x[k] = add(even[k], t);x[k + N / 2] = subtract(even[k], t); }//完整的IFFT实现代码略，与FFT相似int mai//输入序列x(n)int N = sizeof(x) / sizeof(x[0]);//调用FFTfft(x, N);//输出频域序列X(k)for (int k = 0; k < N; k++)printf("X(%d) = %.2f + %.2fi\n", k, x[k].real, x[k].imag);}//调用IFFT//...return 0;```IFFT的实现与FFT类似，只需将其中几处计算公式略作变换即可。

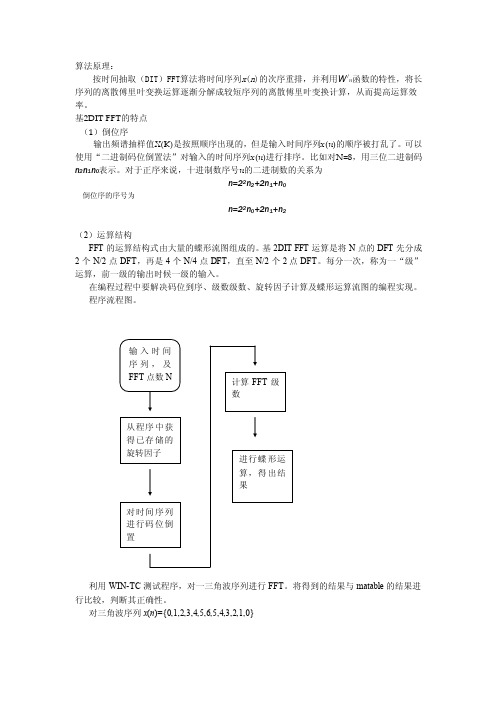
算法原理：按时间抽取（DIT）FFT算法将时间序列x(n)的次序重排，并利用W i n函数的特性，将长序列的离散傅里叶变换运算逐渐分解成较短序列的离散傅里叶变换计算，从而提高运算效率。

基2DIT FFT的特点（1）倒位序输出频谱抽样值X(K)是按照顺序出现的，但是输入时间序列x(n)的顺序被打乱了。

可以使用“二进制码位倒置法”对输入的时间序列x(n)进行排序。

比如对N=8，用三位二进制码n2n1n0表示。

对于正序来说，十进制数序号n的二进制数的关系为n=22n2+2n1+n0倒位序的序号为n=22n0+2n1+n2（2）运算结构FFT的运算结构式由大量的蝶形流图组成的。

基2DIT FFT运算是将N点的DFT先分成2个N/2点DFT，再是4个N/4点DFT，直至N/2个2点DFT。

每分一次，称为一“级”运算，前一级的输出时候一级的输入。

在编程过程中要解决码位到序、级数级数、旋转因子计算及蝶形运算流图的编程实现。

程序流程图。

利用WIN-TC测试程序，对一三角波序列进行FFT。

将得到的结果与matable的结果进行比较，判断其正确性。

对三角波序列x(n)={0,1,2,3,4,5,6,5,4,3,2,1,0}在WIN-TC进行128点FFT，得到前6个结果Matable仿真的前6个结果是XKN2 =Columns 1 through 636.0000 34.2084 -10.3770i 29.1007 -19.4445i 21.4292 -26.1115i 12.2946 -29.6817i 2.9501 -29.9525i前半段波形对比显示WIN-TC结果能保证小数点后2位的精度。

对方波序列x(n),长度为64，前32为1，幅值为1的序列在WIN-TC进行128点FFT，得到前6个结果Matable仿真的前6个结果是Columns 1 through 632.0000 20.8677 -19.8677i 1.0000 -20.3555i -6.2783 - 7.2783i 04.5539 - 3.5539i仿真波形对比显示WIN-TC结果能保证小数点后2位的精度。

F F T算法研究及基2-F F T算法的C语言实现毕业设计 [论文]题目：FFT算法研究及基2-FFT算法的C语言实现学院：电气与信息工程学院专业：电气工程及其自动化姓名： XXX学号： XXXXXX指导老师： XXX完成时间： 2015年06月01日摘要离散傅立叶变换（DFT）常常用于计算信号处理。

DFT算法可以得到信号的频域特性，因为该算法在计算上是密集的，长时间的使用时，计算机不能实时进行信号处理。

所以DFT被发现之后的相当长时间内是没被应用到实际的项目。

到了二十世纪六十年代中期一种新的计算方法被研究者发现出来，它就是FFT。

FFT并不是一种新的获取频域特征的方式，而是离散傅里叶变换的一种快速实现算法。

数字信号处理在当今科技发展中发展很迅速，不但是在传统的通信领域，其他方面也经常用到。

利用快速傅里叶变换，实现了信号频域的变换处理。

对于信号的处理，往往会和数学中的算法联系到一起。

如果处理得当，将会对气象，地理信息等的发展，起到举足轻重的作用，同时对世界其他领域的发展有很大的促进作用。

关键词: FFT算法，C语言，编译实现AbstractDiscrete Fourier Transform (DFT) is often used to calculate the signal processingto obtain frequency domain signals. DFT algorithm can get the frequency domain characteristics of the signal, because the algorithm is computationally intensive, long-time use, the computer is not conducive to real-time signal processing. So DFT since it was discovered in a relatively long period of time is not to be applied to the actual projects until a new fast discrete Fourier calculation method --FFT is found in discrete Fourier transform was able to actually project has been widely used. FFT is not a new way to get the frequency domain, but the discrete Fourier transform of a fast algorithm.Fast Fourier Transform (FFT) is a digital signal processing important tool that the time domain signal into a frequency-domain signal processing. matched filtering has important applications. FFT is a discrete Fourier transform (DFT) is a fast algorithm, it can be a signal from the time domain to the frequency domain. Some signals in the time domain is not easy to observe the characteristics of what is, but then if you change the signal from the time domain to the frequency domain, it is easy to see out of. This design is required to be familiar with the basic principles of FFT algorithm, based onthe preparation of C language program to achieve FFT algorithm real number sequence. Keywords: FFT algorithm, C language compiler to achieve目录摘要 .................................................................................................................................. Abstract (I)目录 .............................................................................................................................. I I 1 引言 01.1 课题背景 01.2 FFT算法的现状 01.3 研究内容 (1)1.4 论文的研究成果 (1)2 数字信号处理综述 (2)2.1 数字信号理论 (2)2.2 数字信号处理的实现 (3)2.3 数字信号处理的应用及特点 (3)3 基本理论 (5)3.1 FFT算法的基本概念 (5)3.1.1离散傅里叶变换（DFT） (5)3.1.2 快速傅里叶变换（FFT） (6)3.2 FFT算法的分类 (7)3.2.1按时间抽取（DIT）的FTT (7)3.2.2 按频率抽取（DIF）的FTT (11)3.2.3 快速傅里叶分裂基FFT算法 (14)3.2.4 N为组合数的FFT——混合基算法 (16)3.3 傅里叶变换的应用 (19)4 基-2FFT算法的C语言实现及仿真 (20)4.1 码位倒序 (20)4.2 蝶形运算 (21)结论 (23)参考文献 (24)附录A (25)附录B (35)致谢 (43)1 引言1.1 课题背景离散傅里叶变换（DFT）可以将有限长序列的的频域也离散化成有现长序列，但是计算量很大，不利于应用于实际工程。

#include <stdio.h>#include <math.h>#include <stdlib.h>#define PI 3.1415926/*This program is used to conduct FFT or IFFT transform based on 2 discomposition data can be loaded by typing on the keyboard or from file.*/typedefstruct{double real;doubleimag;}complex;long NN;long t2t(long n, int M){longnn=0;for(inti=0;i<M;i++){nn=nn+n%2*pow(2,M-1-i);n=n/2;}returnnn;}intdefM(long n){int M=0;while(pow(2,M)<n){M++;}return M;}voiddatain(complex x[],long N){int flag;longi;char s[20];FILE *fpi;doublea,b;printf("Load data from keybord(input 0) or file(input 1)\n");scanf("%d",&flag);if(flag==0){printf("Please enter the data in the form of a,b--a+j*b ending with'*'\n");for(i=0;getchar()!='*';i++)scanf("%lf%lf",&x[i].real,&x[i].imag);while(i<N){x[i].real=0;x[i].imag=0;i++;}}elseif(flag==1){printf("Please input the name of the file with its File type suffix-(eg:data.txt)\n");gets(s);gets(s);//To avoid the quick response to enterfpi=fopen(s,"r");if(!fpi){printf("Open file error");}i=0;while(!feof(fpi)){fscanf(fpi,"%lf",&a);fscanf(fpi,"%lf",&b);x[i].real=a;x[i].imag=b;i++;}fclose(fpi);while(i<N){x[i].real=0;x[i].imag=0;i++;}}}voiddataout(complex x[],long N){longi;for(i=0;i<N;i++)printf("%.3lf+j*%.3lf\n",x[i].real,x[i].imag);}void reverse(complex x[],complex xi[],long n,int m) {longi;long temp;for(i=0;i<n;i++){temp=t2t(i,m);xi[i].real=x[temp].real;xi[i].imag=x[temp].imag;}}complexcom_add(complex x1,complex x2){complex y;y.real=x1.real+x2.real;y.imag=x1.imag+x2.imag;return y;}complexcom_sub(complex x1,complex x2){complex y;y.real=x1.real-x2.real;y.imag=x1.imag-x2.imag;return y;}complexcom_mul(complex x1,complex x2){complex y;y.real=x1.real*x2.real-x1.imag*x2.imag;y.imag=x1.real*x2.imag+x2.real*x1.imag;return y;}complexcom_div(complex x1,complex x2){complex y;double down=x2.real*x2.real+x2.imag*x2.imag;y.real=(x1.real*x2.real+x1.imag*x2.imag)/down;y.imag=(x2.real*x1.imag-x1.real*x2.imag)/down;return y;}voidfft(complex x[],long NN, int M){intm,i,j;longNw,Ni;complexWm,temp;for(m=0;m<M;m++){Nw=pow(2,m+1);Ni=pow(2,m);for(i=0;i<Ni;i++){for(j=i;j<NN;j=j+Nw){Wm.real=cos(2*i*PI/Nw);Wm.imag=-sin(2*i*PI/Nw);temp=com_mul(x[j+Ni],Wm);x[j+Ni]=com_sub(x[j],temp);x[j]=com_add(x[j],temp);}}}}voidifft(complex x[],long NN, int M){intm,i,j;longNw,Ni;complexWm,temp;for(m=0;m<M;m++){Nw=pow(2,m+1);Ni=pow(2,m);for(i=0;i<Ni;i++){for(j=i;j<NN;j=j+Nw){Wm.real=cos(2*i*PI/Nw);Wm.imag=-sin(2*i*PI/Nw);temp=com_mul(x[j+Ni],Wm);x[j+Ni]=com_sub(x[j],temp);x[j]=com_add(x[j],temp);}}}for(i=0;i<NN;i++){x[i].real=x[i].real/NN;x[i].imag=-x[i].imag/NN;}}int main(){longN,i;intM,flag;doublea,b;printf("Please enter the length of the sequence\n");scanf("%ld",&N);M=defM(N);NN=pow(2,M);complexxy[NN];complex xyi[NN];datain(xy,N);for(i=N;i<NN;i++){xy[i].real=0;xy[i].imag=0;}reverse(xy,xyi,NN,M);printf("Please choose FFT(1) or IFFT(-1)\n");scanf("%d",&flag);if(flag==1)fft(xyi,NN,M);elseif(flag==-1)ifft(xyi,NN,M);printf("The initial sequence is:\n");dataout(xy,N);printf("The FFT results are as follows:\n"); dataout(xyi,N);return 0;}。

基2dit-dif-fft与dit-dif-ifft实现,可运行#include#include#include#define MAX 257struct compx{ double real;double imag;} compx ;struct compx EE(struct compx b1, struct compx b2)//两复数相乘{struct compx b3;b3.real = b1.real * b2.real - b1.imag * b2.imag;b3.imag = b1.real * b2.imag + b1.imag * b2.real;return(b3);}void FFT_DIT(struct compx *xin, int N){int f, m, LH, nm, i, k, j, L;double p , ps ;int le,B, ip;double pi;struct compx w, t;LH=N / 2;f=N;for(m = 1;(f = f / 2) != 1; m++){;} //2的m次方=N，m为级数nm = N - 2;j = N / 2;/*变址运算*/for(i = 1;i <= nm; i++){if(i < j){t = xin[j]; xin[j] = xin[i]; xin[i] = t;}k = LH;while(j >= k){j = j - k; k = k / 2;}j = j + k;}/*fft_dit运算*/for(L = 0; L <= m - 1; L++) //每一级{le =(int) pow(2.0, L + 1);//具有相同旋转因子的蝶形运算的间隔B = le / 2; //2的L次方，不同旋转因子的个数，蝶形运算两支间隔pi=3.141592653589793;for(j = 0;j <= B - 1; j++){p = pow(2.0, m - L - 1) * j;ps = 2 * pi / N * p;//旋转因子w.real = cos(ps);w.imag = -sin(ps);for(i = j; i <= N - 1; i = i + le){ip = i + B;t = EE(xin[ip], w);xin[ip].real = xin[i].real - t.real;xin[ip].imag = xin[i].imag - t.imag;xin[i].real = xin[i].real + t.real;xin[i].imag = xin[i].imag + t.imag;}}}return ;}void FFT_DIF(struct compx *xin, int N){int f, m, LH, nm, i, k, j, L;double p, ps ;int le, B, ip;double pi;struct compx w, t;LH = N / 2;f = N;for(m = 1; (f = f / 2) != 1; m++){;}//2的m次方=N，m为级数/*fft_dif运算*/for(L = 0; L <= m - 1; L++) //每一级{le =(int) pow(2.0, m - L);//具有相同旋转因子的蝶形运算的间隔B = le / 2; //2的m - L - 1次方，不同旋转因子的个数，蝶形运算两支间隔pi = 3.141592653589793;for(j = 0; j <= B - 1; j++){p = pow(2.0, L) * j;ps = 2 * pi / N * p;//旋转因子w.real = cos(ps);w.imag = -sin(ps);for(i = j; i <= N-1; i = i + le){ip = i + B;t = xin[i];xin[i].real = t.real + xin[ip].real;xin[i].imag = t.imag + xin[ip].imag;xin[ip].real = t.real - xin[ip].real;xin[ip].imag = t.imag - xin[ip].imag;xin[ip] = EE(xin[ip], w);}}}nm = N - 2;j = N / 2;/*变址运算*/for(i = 1; i <= nm; i++){if(i < j){t = xin[j]; xin[j] = xin[i]; xin[i] = t;} k = LH;while(j >= k){j = j - k; k = k / 2;}j = j + k;}return ;}void IFFT_DIT(struct compx *xin, int N){int f, m, LH, nm, i, k, j, L;double p, ps ;int le, B, ip;double pi;struct compx w, t;LH = N / 2;f=N;for(m = 1; (f = f / 2) != 1; m++){;}//2的m次方=N，m为级数/*fft_dif运算*/for(L = 0; L <= m - 1; L++) //每一级{le = (int) pow(2.0, m - L);//具有相同旋转因子的蝶形运算的间隔B = le / 2; //2的m - L - 1次方，不同旋转因子的个数，蝶形运算两支间隔pi=3.141592653589793 ;for(j = 0; j <= B-1; j++){p = pow(2.0, L) * j;ps = -2 * pi / N * p;//旋转因子w.real = cos(ps);w.imag = -sin(ps);for(i = j; i <= N - 1; i = i + le){t = xin[i];xin[i].real = (t.real + xin[ip].real) * 0.5;xin[i].imag = (t.imag + xin[ip].imag) * 0.5; xin[ip].real = (t.real - xin[ip].real) * 0.5; xin[ip].imag = (t.imag - xin[ip].imag) * 0.5; }}}nm = N - 2;j = N / 2;/*变址运算*/for(i = 1; i <= nm; i++){if(i < j){t = xin[j]; xin[j]=xin[i]; xin[i]=t;}k = LH;while(j >= k){j = j - k; k = k / 2;}j = j + k;}return ;}void IFFT_DIF(struct compx *xin, int N) {int f, m, LH, nm, i, k, j, L;double p, ps ;int le, B, ip;double pi;struct compx w, t;f = N;for(m = 1; (f = f / 2) != 1; m++){;}//2的m次方=N，m为级数nm = N - 2;j = N / 2;/*变址运算*/for(i = 1; i <= nm; i++){if(i < j){t = xin[j]; xin[j] = xin[i]; xin[i] = t;}k = LH;while(j>=k){j = j - k; k = k / 2;}j = j + k;}/*fft_dit运算*/for(L = 0; L <=m - 1; L++) //每一级{le=(int) pow(2.0, L + 1);//具有相同旋转因子的蝶形运算的间隔B = le / 2; //2的L次方，不同旋转因子的个数，蝶形运算两支间隔pi=3.141592653589793 ;for(j = 0; j <= B - 1; j++){p = pow(2.0, m - L - 1) * j;ps = -2 * pi / N * p;//旋转因子w.real = cos(ps);w.imag = -sin(ps);for(i = j; i <= N - 1; i = i + le){ip = i + B;t = EE(xin[ip], w);xin[ip].real = (xin[i].real-t.real) * 0.5;xin[ip].imag = (xin[i].imag-t.imag) * 0.5; xin[i].real = (xin[i].real+t.real) * 0.5;xin[i].imag = (xin[i].imag+t.imag) * 0.5; }}}return ;}double result[MAX];struct compx s[MAX];int Num = 128;const double pp = 3.141592653589793 ;int main(){int i;char method; // fft and ifft methodfor(i = 0;i < Num; i++){s[i].real = sin(pp*i/256);s[i].imag = 0;}printf("Input the fft decimation method(T or t for dit, F or f for dif): ");method = getchar();if (method == 'T' || method == 't')FFT_DIT(s, Num);else if (method == 'F' || method == 'f')FFT_DIF(s, Num);else{printf("INPUT ERROR! No such method"); return 0;}printf("fft results:\n");for(i = 0; i < Num; i++){printf("%.4f", s[i].real);printf("+j(%.4f)\n", s[i].imag);//result[i]=sqrt(pow(s[i].real,2)+pow(s[i].imag,2));}printf("Input the ifft decimation method(T or t for dit, F or f for dif): ");int c;while ((c = getchar()) != '\n' && c != EOF) ; // 去除缓冲区内多余（脏）的回车或文件结束符method = getchar ();if (method == 'T' || method == 't')IFFT_DIT(s, Num);else if (method == 'F' || method == 'f')IFFT_DIF(s, Num);else{printf("INPUT ERROR! No such method");return 0;}printf("ifft results:\n");for(i = 0; i < Num; i++){printf("%.4f", s[i].real);printf("+j(%.4f)\n", s[i].imag);//result[i]=sqrt(pow(s[i].real,2)+pow(s[i].imag,2)); }return 0;}。

实序列FFT算法的C语言实现学生：XX 指导教师：XX内容摘要：DFT和IDFT是数字信号分析与处理中的一种重要运算和变换，但直接根据定义计算DFT时，运算量大，不能实时得到计算结果。

特别是在实际应用中，N都取得比较大，此时，由于乘法和加法的次数都近似与N的平方成正比，这将极大增加DFT计算所需时间。

为此，提出了许多DFT和IDFT的快速算法，称为快速傅里叶变换（FFT）和快速傅里叶反变换（IFFT）。

本文较为系统地阐述了快速傅里叶变换的算法原理然后用MATLA实现了快速傅里叶变换。

论文首先首要介绍了FT与DFT的定义、DFT与FFT的关系,然后重点介绍基2时域抽取FFT算法以及其原理和运算流图，再应用C语言实现了实序列的FFT。

最后在Matlab 软件上进行仿真，仿真结果验证了设计的正确性。

关键词：傅里叶变换快速傅立叶变换Matlab 仿真Realization of FFT algorithm for real sequenceWith C p rogramAbstract : DFTand IDFT are important transform and processing in digital signalprocessing. However, there are large amount of computation by directly calculati ng accord ing to the defi niti on of DFT. Esp ecially in the p racticalapp licati on, N is bigger, at this time, because the time of mult ip licatio n andadditi on are app roximately prop orti onal to the square of N, which will greatlyin crease the calculatio n time n eeded for DFT. Therefore, man yDFTa nd IDFT fastalgorithm are raised, which are called FFT and IFFT.In this paper relatively systematically elaborated the fast Fourier tran sform algorithm principle and use MATLABoftware to realize the fast Fourier tran sform. The paper first introduces the definition of FT and DFT,the relationship betwee n DFT and FFT, and the n mainly in troduces DIT-FFT ,in clud ing its principle andop erati on flow diagram, and fin ally used C Ian guage to realize the real sequeneeFFT.The desig ns are simulated in Matlab software, the results of the simulationcon firm the exact ness of the desig n.Keywords : Fourier transformation fast Fourier tran sformatio n Matlab simulati on、F —前言序列的FT 和DFT.1.1 序列的FT1.2 序列的DFT1.2.1 DFT 的定义和计算1.2.2 实序列的DFTFFT 算法2.1 基2时域抽取FFT算法2.2 实序列的FFT算法实序列FFT算法的C语言实现目录3.1 3.2 3.3 3.4 VS20103.1.13.1.2实序列3.2.13.2.2实序列3.3.13.3.2简介新建项目新建文件FFT算法子程序倒序蝶形运算FFT算法主程序原始序列的产生和读取计算结果的显示和输出运行结果分析结束语录：参考文献：101215151616 3.4.1 计算结果数据分析342 N 点DFT波形分析1717202127 2.1.1 基本原理2.1.2 DIT-FFT 算法的运算流图2.1.3 DIT-FFT 算法的运算量和存储量实序列FFT 算法的C 语言实现1刖言 在实际的数字系统中, DFT 是一种得到了广泛的应用的、重要的信号处理手段，但 它的运算效率非常低。

fft算法c语言实现快速傅里叶变换（FFT）是一种高效的离散傅里叶变换算法，用于计算信号在频域的表示。

下面是一个简单的使用 C 语言实现的 FFT 算法示例，它可以用于对输入的时域信号进行离散傅里叶变换。

```c#include <stdio.h>#include <stdlib.h>#include <math.h>#define N 16// 复数结构体typedef struct {double real;double imag;} Complex;// 初始化复数void initComplex(Complex *c, double real, double imag) {c->real = real;c->imag = imag;}// FFT 算法void fft(Complex *c, int n) {int i, j, k;Complex w, u, v;// 层次遍历for (i = 1; i < n; i <<= 1) {// 旋转因子w.real = cos(2 * M_PI * i / n);w.imag = -sin(2 * M_PI * i / n);for (j = 0; j < n; j += i) {for (k = 0; k < i / 2; k++) {u.real = c[j + k].real;u.imag = c[j + k].imag;v.real = c[j + i / 2 + k].real;v.imag = c[j + i / 2 + k].imag;c[j + k].real = u.real + w.real * v.real - w.imag * v.imag; c[j + k].imag = u.imag + w.real * v.imag + w.imag * v.real; c[j + i / 2 + k].real = u.real - w.real * v.real + w.imag * v.imag; c[j + i / 2 + k].imag = u.imag - w.real * v.imag - w.imag * v.real; }}}}// 打印复数void printComplex(Complex c) {printf("%f + %fi\n", c.real, c.imag);}int main() {Complex c[N];// 输入的时域信号for (int i = 0; i < N; i++) {c[i].real = rand() / RAND_MAX;c[i].imag = rand() / RAND_MAX;}printf("输入的时域信号：\n");// 打印输入的时域信号for (int i = 0; i < N; i++) {printComplex(c[i]);}fft(c, N);printf("经过 FFT 变换后的频域信号：\n");// 打印经过 FFT 变换后的频域信号for (int i = 0; i < N; i++) {printComplex(c[i]);}return 0;}```上述代码是一个简单的 C 语言实现的 FFT 算法示例。

C语言实现FFT快速傅里叶变换（Fast Fourier Transform, FFT）是一种高效进行离散傅里叶变换（Discrete Fourier Transform, DFT）计算的算法。

它通过利用对称性和递归的方法，将O(n^2)的计算复杂度优化为O(nlogn)。

本文将介绍C语言实现FFT的基本步骤和代码。

首先，需要定义一个复数结构体来表示复数，包含实部和虚部两个成员变量：```ctypedef structdouble real; // 实部double imag; // 虚部```接着，需要实现FFT的关键函数，包括以下几个步骤：1. 进行位逆序排列（bit-reversal permutation）：FFT中的输入数据需要按照位逆序排列，这里使用蝶形算法来实现位逆序排列。

先将输入序列按照索引位逆序排列，再将复数序列按照实部和虚部进行重新排列。

```cint i, j, k;for (i = 1, j = size / 2; i < size - 1; i++)if (i < j)temp = data[j];data[j] = data[i];data[i] = temp;}k = size / 2;while (j >= k)j=j-k;k=k/2;}j=j+k;}```2. 计算旋转因子（twiddle factor）：FFT中的旋转因子用于对复数进行旋转变换，这里采用的旋转因子为e^( -2*pi*i/N )，其中N为DFT点数。

```cint i;double angle;for (i = 0; i < size; i++)angle = -2 * M_PI * i / size;twiddleFactors[i].real = cos(angle);twiddleFactors[i].imag = sin(angle);}```3.执行蝶形算法计算DFT：蝶形算法是FFT算法的核心部分，通过递归地将DFT问题一分为二，并将计算结果根据旋转因子进行两两合并，最终得到FFT结果。

#include <stdio.h>#include <math.h>#include <stdlib.h>#define N 1000/*定义复数类型*/typedef struct{double real;double img;}complex;complex x[N], *W; /*输入序列,变换核*/int size_x=0; /*输入序列的大小，在本程序中仅限2的次幂*/ double PI; /*圆周率*/void fft(); /*快速傅里叶变换*/void ifft();void initW(); /*初始化变换核*/void change(); /*变址*/void add(complex ,complex ,complex *); /*复数加法*/void mul(complex ,complex ,complex *); /*复数乘法*/void sub(complex ,complex ,complex *); /*复数减法*/void divi(complex ,complex ,complex *);/*复数除法*/void output();int main(){int i,method; /*输出结果*/system("cls");PI=atan(1)*4;printf("Please input the size of x:\n");scanf("%d",&size_x);printf("Please input the data in x[N]:\n");for(i=0;i<size_x;i++)scanf("%lf%lf",&x[i].real,&x[i].img);initW();printf("Use FFT(0) or IFFT(1) \n");scanf("%d",&method);if(method==0)fft();elseifft();output();return 0;}/*快速傅里叶变换*/void fft(){int i=0,j=0,k=0,l=0;complex up,down,product;change();for(i=0;i< log(size_x)/log(2) ;i++){ /*一级蝶形运算*/l=1<<i;for(j=0;j<size_x;j+= 2*l ){ /*一组蝶形运算*/ for(k=0;k<l;k++){ /*一个蝶形运算*/mul(x[j+k+l],W[size_x*k/2/l],&product);add(x[j+k],product,&up);sub(x[j+k],product,&down);x[j+k]=up;x[j+k+l]=down;}}}}/*快速傅里叶逆变换*/void ifft(){int i=0,j=0,k=0,l=size_x;complex up,down;for(i=0;i< (int)( log(size_x)/log(2) );i++){ /*一级蝶形运算*/ l/=2;for(j=0;j<size_x;j+= 2*l ){ /*一组蝶形运算*/ for(k=0;k<l;k++){ /*一个蝶形运算*/add(x[j+k],x[j+k+l],&up);up.real/=2;up.img/=2;sub(x[j+k],x[j+k+l],&down);down.real/=2;down.img/=2;divi(down,W[size_x*k/2/l],&down);x[j+k]=up;x[j+k+l]=down;}}}change();}/*初始化变换核*/void initW(){int i;W=(complex *)malloc(sizeof(complex) * size_x);for(i=0;i<size_x;i++){W[i].real=cos(2*PI/size_x*i);W[i].img=-1*sin(2*PI/size_x*i);}}/*变址计算，将x(n)码位倒置*/void change(){complex temp;unsigned short i=0,j=0,k=0;double t;for(i=0;i<size_x;i++){k=i;j=0;t=(log(size_x)/log(2));while( (t--)>0 ){j=j<<1;j|=(k & 1);k=k>>1;}if(j>i){temp=x[i];x[i]=x[j];x[j]=temp;}}}/*输出傅里叶变换的结果*/void output(){int i;printf("The result are as follows\n");for(i=0;i<size_x;i++){printf("%.4f",x[i].real);if(x[i].img>=0.0001)printf("+%.4fj\n",x[i].img);else if(fabs(x[i].img)<0.0001)printf("\n");else printf("%.4fj\n",x[i].img);}}void add(complex a,complex b,complex *c){c->real=a.real+b.real;c->img=a.img+b.img;}void mul(complex a,complex b,complex *c){c->real=a.real*b.real - a.img*b.img;c->img=a.real*b.img + a.img*b.real;}void sub(complex a,complex b,complex *c){c->real=a.real-b.real;c->img=a.img-b.img;}void divi(complex a,complex b,complex *c){c->real=( a.real*b.real+a.img*b.img )/( b.real*b.real+b.img*b.img);c->img=( a.img*b.real-a.real*b.img)/(b.real*b.real+b.img*b.img); }。