[第30讲]小升初几何_(五大模型_蝴蝶模型与燕尾模型) (1)

平面几何常考五大模型---（解答几何题的五大法宝）等积变换、鸟头、蝴蝶、相似、燕尾思路提示：在求边长之比时常转化为面积之比，求面积之比常转化为边长之比。

模型一：等积变化原理：两个三角形高相等，面积之比等于对应底边之比。

bS 1︰S 2 =a ︰b ；模型一的拓展： 等分点结论（“鸟头定理”）:如下图，三角形AED 占三角形ABC 面积的23×14=16模型二：等积变化原理之四边形应用S 4S 3s 2s 1O DC BA141423213S S =S S S S DO OB S S +==+模型三：梯形中比例关系（“梯形蝴蝶定理”）(1)相似图形，面积比等于对应边长比的平方S 1︰S 3=a 2︰b2（2）S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab （3）S 2=S 4 ；（4）141423213S S =S S S S DO OB S S +==+ :模型四：相似三角形性质①a b c hA B C H=== ; ②相似三角形面积之比等于对应连长之比的平方S 1︰S 2=a 2︰A 2hh H cb a CB Aac b HC B模型五：燕尾定理F ED CBAS △ABG ：S △AGC ＝S △BGE ：S △GEC ＝BE ：EC ； S △BGA ：S △BGC ＝S △AGF ：S △GFC ＝AF ：FC ； S △AGC ：S △BCG ＝S △ADG ：S △DGB ＝AD ：DB ；【例1】：如右图，在△ABC 中，BE=3AE ，CD=2AD ．若△ADE 的面积是1平方厘米，那么三角形ABC 的面积是多少？【解答】连接BD,S △ABD 和S △ AED 同高，面积比等于底边比，所以三角形ABD 的面积是4，S △ABD 和S △ABC 同高面积比等于底边比，三角形ABC 的面积是ABD 的3倍，是12. 【总结】要找准那两个三角形的高相同。

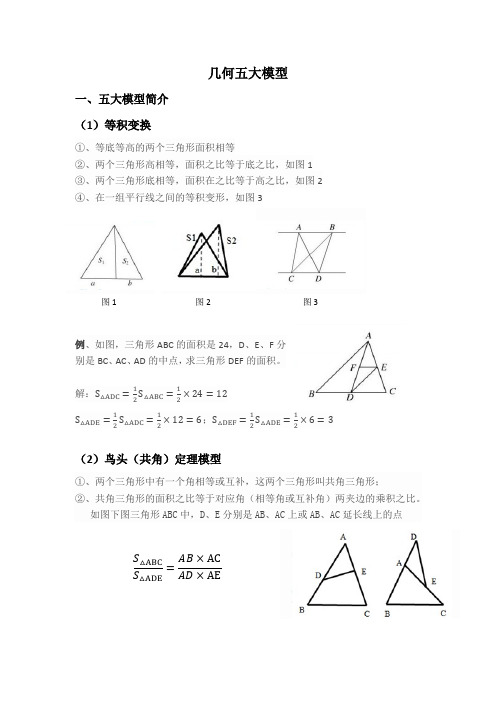
几何五大模型一、五大模型简介（1）等积变换①、等底等高的两个三角形面积相等②、两个三角形高相等，面积之比等于底之比，如图1③、两个三角形底相等，面积在之比等于高之比，如图2④、在一组平行线之间的等积变形，如图3图1 图2 图3例、如图，三角形ABC的面积是24，D、E、F分别是BC、AC、AD的中点，求三角形DEF的面积。

解：S△ADC=12S△ABC=12×24=12S△ADE=12S△ADC=12×12=6；S△DEF=12S△ADE=12×6=3（2）鸟头（共角）定理模型①、两个三角形中有一个角相等或互补，这两个三角形叫共角三角形；②、共角三角形的面积之比等于对应角（相等角或互补角）两夹边的乘积之比。

如图下图三角形ABC中，D、E分别是AB、AC上或AB、AC延长线上的点S△ABC S△ADE =AB×AC AD×AE例、如图在ΔABC中，D在BA的延长线上，E在AC上，且AB：AD=5:2，AE：EC=3:2，△ADE的面积为12平方厘米，求ΔABC 的面积。

解：由题意知：S△ABCS△ADE =AB×ACAD×AE=52×53=256∴S△ABC=256×S△ADE=256×12=50(平方厘米)（3）蝴蝶模型1、梯形中比例关系(“梯形蝴蝶定理”)①S2=S4(梯形两翼相等)②S1:S3:S2:S4=a2:b2:ab:ab③梯形S对应的分数为（a+b)2例、如图，梯形ABCD，AB与CD平行，对角线AC、BD交于点O，已知△AOB、△BOC的面积分别为25平方厘米、35平方厘米，求梯形ABCD的面积。

解：S△AOB:S△BOC=25:35=5:7S△AOB:S△DOC=AB2:DC2=52:72=25：49∴S△DOC=49又S△AOD=S△BOC=35∴S ABCD=25+35+35+49=144(平方厘米)2、任意四边形中的比例关系(“蝴蝶定理”)：①S1:S2=S4:S3或S1×S3=S2×S4②AO:OC=S1:S4=S2:S3=(S1+S2):(S4+S3)例、如图，四边形ABCD的对角线AC、BD交于点O，如果三角形ABD的面积等于三角形BCD面积的1/3，且AO=2，求OC解：AO:OC=S△ABD:S△BCD=1:3OC=2×3=6（4）相似模型1、相似三角形：形状相同,大小不相等的两个三角形相似；2、寻找相似模型的大前提是平行线：平行于三角形一边的直线和其他两边或两边延长线相交，所构成的三角形与原三角形相似。

甘、升初几何重点考查內彖」苗内容提要蝴蝶模型审喩⑴任意四边形中的比例关系:①S ： $2 =$4 : 5*3 或者51 XS3 =5*2X54®AO : OC = (S+&) : (&+6)⑵梯形中比例关系（“梯形蝴蝶定理”）:(D52=54②S I : ® ： & ： & ：SABCD=a2 : b2'• ah ： ab : (q + />)2几何模型常用方法1. 加辅助线构造模型2. 在图上标份数思想3. 选择对称思想如图，长方形ABCD中，BE： EC=2 : 3, DF \ FC=\ : 2,三角形DFG的而积为2平方厘米，求长方形ABCD的面积。

C在下图的正方形ABCD中，E是BC边的中点，AE与BD相交于F点，三角形的面积为1平方厘米，那么正方形ABCD面积是多少平方厘米。

如图，在梯形ABCD中，AD : BE=4 : 3, BE : EC=2 : 3,且△BOE的面积比△AOD的面积小10平方厘米。

梯形ABCD的面积是多少平方厘米？在三角形ABC中，三角形AEO的面枳是1,三角形ABO的面积是2,三角形的面积是3,则四边形DCEO的面积是多少？如图，E 在 AC 上，D 在BC 上，且AE : EC=2 : 3, BD : DC= \ : 2, AD 与BE 交于点F。

四边形DFEC的面积等于22cm2,则三角形ABC的面积是_____________ 。

©/温故知新©1.熟记蝴蝶和燕尾模型的特点2.加辅助线构造模型3.在图上标倍数和份数4.方程是个好方法在线测试题温馨提示：请在线作答，以便及时反馈孩子的薄弱环节。

如图在△ ABC中,DC EA FB 2求的面积的仁~DB~~EC~~FA~3 '求AABC的面积且1-已知长方形ADEF的面积是16,三角形AD3的面积是3, 么三角形ABC的面积是_______________ oA. 2.5三角形ACF的面积是4,那4.5 C. 6.5 D. 8.54 9 1 A.- 3 氏I ，.如图，正方形ABCD 面积为1, M 是AD 边上的中点，求图屮阴影部分的面积。

小升初几何常考五大模型（等积变换、鸟头、蝴蝶、相似、燕尾）下面给大家整理小升初数学几何常考五大模型（等积变换模型、鸟头定理、蝴蝶定理、相似模型、燕尾定理）（一）等积变换模型性质与应用简介平面几何问题，是历年小升初的必考题目，也在各大杯赛中占有很大比例，这些题目都是以等积变形为主导思想，结合五大模型的变化应用交织而成的，这一期我们讲解了解一下五大模型第一块——等积变换模型。

1.等积变换模型（1）等底等高的两个三角形面积相等；（2）两个三角形高相等，面积比等于它们的底之比；(3)如右图夹在一组平行线之间的等积变形，S△ACD=S△BCD反之，S△ACD=S△BCD，则可知直线AB∥直线CD等积变换模型例题讲解与课后练习题（一）例题讲解与分析【例1】：如右图，在△ABC中，BE=3AE，CD=2AD．若△ADE 的面积是1平方厘米，那么三角形ABC的面积是多少？【解答】连接BD,S△ABD和S△ AED同高，面积比等于底边比，所以三角形ABD的面积是4，S△ABD和S△ABC同高面积比等于底边比，三角形ABC的面积是ABD的3倍，是12.【总结】要找准那两个三角形的高相同。

【例2】：如图，四边形ABCD中，AC和BD相交于O点，三角形ADO的面积=5，三角形DOC的面积=4，三角形AOB的面积=15，求三角形BOC的面积是多少？【解答】S△ADO=5,S△DOC=4根据结论2，△ADO与△DOC同高所以面积比等于底的比,即AO/OC=5:4同理S△AOB/S△BOC=AO/OC=5:4,因为S△AOB=15所以S△BOC=12。

【总结】从这个题目我们可以发现，题目的条件和结论都是三角形的面积比，我们在解题过程中借助结论2，先把面积比转化成线段比，再把线段比用结论2转化成面积比，解决了问题。

事实上，这2次转化的过程就相当于在条件和结论中搭了一座'桥梁'，请同学们体会一下。

（二）鸟头定理（共角定理）模型平面几何问题，是历年小升初的必考题目，也在各大杯赛中占有很大比例，这些题目都是以等积变形为主导思想，结合五大模型的变化应用交织而成的，第二期我们讲解了解一下五大模型第二块——鸟头定理（共角定理）模型。

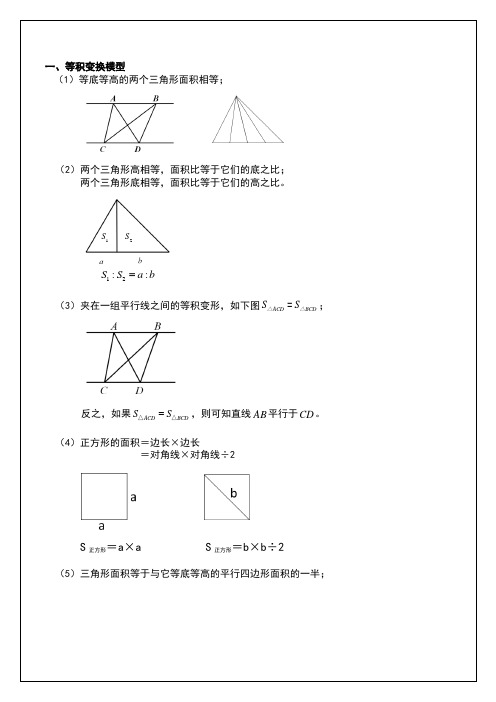
）两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比。

12::S S a b =）夹在一组平行线之间的等积变形，如下图反之，如果ACD S S =△△）正方形的面积＝边长×边长 ＝对角线×对角线÷2S 正方形＝a ×a S 正方形＝b×b÷2）三角形面积等于与它等底等高的平行四边形面积的一半；1S 2S图1 图2三、蝴蝶定理模型任意四边形中的比例关系(“蝴蝶定理”)：①1243::S S S S =或者1S ②()(12::AO OC S S S =+蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。

①2213::S S a b =②21324::::S S S S a b =③梯形S 的对应份数为(金字塔模型 沙漏模型AD AE DE AB AC BC ===2::ADE ABC S S AF =△△△ABG ∶S △AGC ＝S △BGE ∶S △EGC ＝△BGA ∶S △BGC ＝S △AGF ∶S △FGC ＝△AGC ∶S △BCG ＝S △ADG ∶S △DG B ＝典型例题精讲、一个长方形分成4个不同的三角形，绿色三角形面积是长方形面积的两条线段把三角形分为三个三角形和一个四边形，如图所示，三个三角形的面积分别是边延长3倍到F。

如相交于O，若△AOM、△ABO 的面积等于三角BCDCG，HD＝DA，求四边形到正方形顶点C、D连成一个三角形，，已知AH＝5cm，HF ，求AF∶FB。

边上的四等分点，AD与BG交于M，平方厘米，则△ABC的面积是，CF＝2DF，连接BF，，设正方形MGQA的面积∶1，四边形DOEC的面积是2∶3，若三角形ABC的面积是9平方厘米，三角形BOC的面积为25平。

如果三角形BCD的面积等于三角的长度的（）倍。

1.6，求梯形ABCD的面积。

FB的长是3。

那么，的面积是多少？。

几何五大模型一、五大模型简介（1）等积变换模型1、等底等高的两个三角形面积相等；2、两个三角形高相等，面积之比等于底之比，如图①所示，S[sub]1[/sub]：S[sub]2[/sub]=a:b；3、两个三角形底相等，面积在之比等于高之比，如图②所示，S[sub]1[/sub]：S[sub]2[/sub]=a:b；4、在一组平行线之间的等积变形，如图③所示，S[sub]△ACD[/sub]=S[sub]△BCD[/sub]；反之，如果S[sub]△ACD[/sub]=S[sub]△BCD[/sub]，则可知直线AB平行于CD。

例、如图，三角形ABC的面积是24，D、E、F分别是BC、AC、AD的中点，求三角形DEF的面积。

（2）鸟头（共角）定理模型1、两个三角形中有一个角相等或互补，这两个三角形叫共角三角形；2、共角三角形的面积之比等于对应角（相等角或互补角）两夹边的乘积之比。

如图下图三角形ABC中，D、E分别是AB、AC上或AB、AC延长线上的点则有：S[sub]△ABC[/sub]：S[sub]△ADE[/sub]=（AB×AC）：（AD×AE）我们现在以互补为例来简单证明一下共角定理！如图连接BE，根据等积变化模型知，S[sub]△ADE[/sub]：S[sub]△ABE[/sub]=AD：AB、S[sub]△ABE[/sub]：S[sub]△CBE[/sub]=AE：CE，所以S[sub]△ABE[/sub]：S[sub]△ABC[/sub]=S[sub]△ABE[/sub]：（S[sub]△ABE[/sub]+S[sub]△CBE[/sub]）=AE：AC，因此S[sub]△ADE[/sub]：S[sub]△ABC[/sub]=（S[sub]△ADE[/sub]：S[sub]△ABE[/sub]）×（S[sub]△ABE[/sub]：S[sub]△ABC[/sub]）=（AD：AB）×（AE：AC）。

1
(★★★)
如图，长方形ABCD 中，BE ∶EC ＝2∶3，DF ∶FC ＝1∶2，三角形DFG 的面积为2平方厘米，求长方形ABCD 的面积。

(★★★)
在下图的正方形ABCD 中，E 是BC 边的中点， AE 与BD 相交于F 点，三角形BEF 的面积为1平方厘米，那么正方形ABCD 面积是多少平方厘米。

(★★★)
如图，在梯形ABCD 中，AD ∶BE ＝4∶3，BE ∶EC ＝2∶3，且△BOE 的面积比△AOD 的面积小10平方厘
米。

梯形ABCD 的面积是多少平方厘米？
(★★★)
在三角形ABC 中，三角形AEO 的面积是1，三角形ABO 的面积是2，三角形BOD 的面积是3，则四边形DCEO 的面积是多少？
(★★★★)
如图，E 在AC 上，D 在BC 上，且AE ∶EC ＝2∶3，BD ∶DC ＝1∶2，AD 与BE 交于点F 。

四边形DFEC 的面积等于22cm 2，则三角形ABC 的面积是______。

(★★★★★)
如图在△ABC 中，2
3
DC EA FB DB EC FA ===，
求GHI ABC ∆∆的面积的面积的值。

实用标准文案平面几何图形板块一、经典模型回顾知识点1.共高定理共高定理鸟头模型用途：根据大面积求小面积。

例11AB , BE =1 BC , CF =1 CA，则三角形DEF的面3 4 5如图，三角形ABC的面积为1,且AD =积是_______ 。

V --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- 勺精彩文档例2知识点2：蝴蝶模型S J\ABD _—Q结论：-1.「皿0 c2. 81X83=82X84用途：借助面积比来反求线段比。

如图，正方形ABCD的面积是64平方厘米，正方形CEFG的面积是36平方厘米，DF与BG相交于O。

则DBO的面积等于多少平米厘米？第2页共9页实用标准文案知识点3：梯形蝴蝶结论：1. S =S4. S =a 2份，S =b 2份,S =S =ab 份；S =(a +b )2份 2 3用途：梯形中的面积比例关系。

如图所示，在梯形ABCD 中，AB//CD ,对角线AC , BD 相交于点。

，已知AB =5, CD =3, 且梯形ABCD 的面积为4,求三角形OAB 的面积。

精彩文档知识点4：燕尾定理S^4co DC结论: 用途：推面积间的比例关系。

例5【阶段总结1】1.五大模型分别是什么？各有什么妙用？2.每个模型中都应注意的小技巧有哪些?板块二、综合运用（一）三条边长分别为5、12、13的直角三角形如图所示，将它的短直角边对折到斜边上去，与斜边相重合，问图中阴影部分的面积是多少？- --------------------------------------------------------------------------------------------------- J第4页共9页实用标准文案例7r一一一一—一―一―一―— - ----- ——一・—一——————一—■一・一一― .：如图，在△ ABC中，△ AEO的面积是1,A ABO的面积是2,A BOD的面积是3,则四边形DCEO的面积是多少？I 」精彩文档板块三、综合运用（二）例10（2008年日本小学算术奥林匹克初小组初赛）如图，阴影部分四边形的外接图形是边长为10cm的正方形，则阴影部分四边形的面积是cm2。