中考数学 第一编 教材知识梳理篇 第四章 图形的初步认识与三角形、四边形 第五节 多边形与平行四边形试题

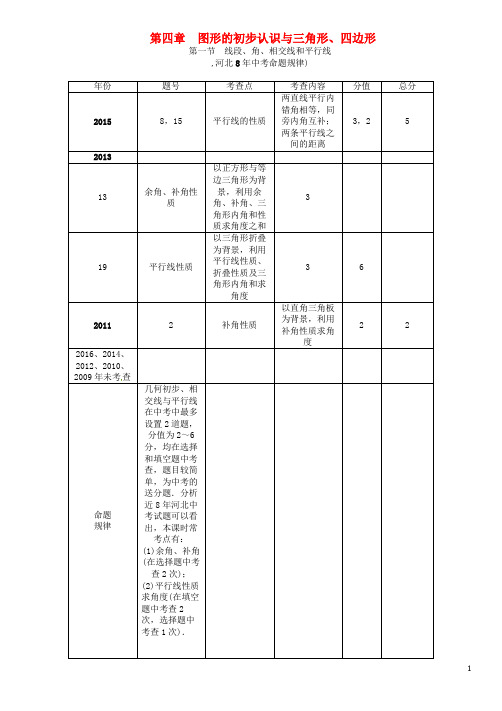
第四章图形的初步认识与三角形、四边形第一节线段、角、相交线和平行线,河北8年中考命题规律)年份题号考查点考查内容分值总分20158，15 平行线的性质两直线平行内错角相等，同旁内角互补；两条平行线之间的距离3，2 5201313 余角、补角性质以正方形与等边三角形为背景，利用余角、补角、三角形内角和性质求角度之和319 平行线性质以三角形折叠为背景，利用平行线性质、折叠性质及三角形内角和求角度3 62011 2 补角性质以直角三角板为背景，利用补角性质求角度2 22016、2014、2012、2010、2009年未考查命题规律几何初步、相交线与平行线在中考中最多设置2道题，分值为2～6分，均在选择和填空题中考查，题目较简单，为中考的送分题．分析近8年河北中考试题可以看出，本课时常考点有：(1)余角、补角(在选择题中考查2次)；(2)平行线性质求角度(在填空题中考查2次，选择题中考查1次)．命题预测预计2017年中考，本节内容仍会考查，且以利用平行线的性质计算角度为主，题型为选择或填空题.,河北8年中考真题及模拟)平行线性质求角度(3次)1．(2015河北8题3分)如图，AB∥EF，CD⊥EF，∠BAC＝50°，则∠ACD＝( C) A．120°B．130°C．140°D．150°(第1题图)(第2题图)2．(2015河北15题2分)如图，点A，B为定点，定直线l∥AB，P是l上一动点，点M，N分别为PA，PB的中点，对于下列各值：①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．其中会随点P的移动而变化的是( B)A．②③B．②⑤C．①③④D．④⑤3．(2011河北2题2分)如图，∠1＋∠2等于( B)A．60°B．90°C．110°D．180°4．(2016河北保定十七中一模)如图，点O在直线AB上，射线OC平分∠DOB.若∠COB＝35°，则∠AOD等于( C)A．35°B．70°C．110°D．145°(第4题图)(第5题图)5．(2016河北石家庄四十三中一模)如图，三条直线相交于点O.若OC⊥AB，∠1＝56°，则∠2等于( B)A．30°B．34°C．45°D．56°6．(2016张家口模拟)如图，直线a，b及木条c在同一平面上，将木条c绕点O旋转到与直线a平行，其最小旋转角为( B)A．100°B．90°C．80°D．70°(第6题图)(第7题图) 7．(2015唐山路北区一模)如图，直线l1∥l2，∠CAB＝125°，∠ABD＝85°，则∠1＋∠2等于( A)A．30°B．35°C．36°D．40°8．(2016河北石家庄四十三中一模)如图，直线AB，CD被直线EF所截，AB∥CD，∠1＝110°，则∠2等于( B)A．65°B．70°C．75°D．80°(第8题图)(第9题图)9．(2013河北19题3分)在四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B＝__95__°.10．(2016河北石家庄四十中一模)一副三角板如图所示放置，则∠AOB＝__105__°.11．(2016河北石家庄二十八中二模)已知三条不同的直线a，b，c在同一平面内，有下列四个命题：①如果a∥b，a⊥c，那么b⊥c；②如果b∥a，c∥a，那么b∥c；③如果b⊥a，c⊥a，那么b⊥c；④如果b⊥a，c⊥a，那么b∥c.其中真命题的是__①②④__.(填写所有真命题的序号)12．(2016河北唐山友谊中学一模)如图，AF，BD，CE，AC，DF均是直线，∠EQF＝∠APB，∠C＝∠D.求证：∠A＝∠F.证明：∵∠APB＝∠DPF，∠APB＝∠EQF，∴∠DPF＝∠EQF.∴DB∥EC.∴∠FEC＝∠D.又∵∠C＝∠D，∴∠FEC＝∠C.∴DF∥AC.∴∠A＝∠F.,中考考点清单)线段与直线1．线段(1)定义：线段的直观形象是拉直的一段线．(2)基本事实：两点之间的所有连线中，线段最短．(3)线段的和与差：如图(1)，已知两条线段a和b，且a>b，在直线l上画线段AB＝a，BC＝b，则线段AC就是线段a 与b 的和，即AC ＝__a ＋b__．如图(2)，在直线l 上画线段AB ＝a ，在AB 上画线段AD ＝b ，则线段DB 就是线段a 与b 的差，即DB ＝a －b.(4)线段的中点：如图(3)，线段AB 上的一点M ，把线段AB 分成两条线段AM 与MB.如果AM ＝MB ，那么点M 就叫做线段AB 的中点，此时有__AM__＝MB ＝12AB ，AB ＝2AM ＝2MB.2．直线(1)定义：沿线段向两方无限延伸所形成的图形．(2)基本事实：经过两点有一条直线，并且只有一条直线．角及角平分线3．角的分类 (1)分类(2)周角、平角、直角之间的关系和度数 1周角＝2平角＝4直角＝360°，1平角＝2直角＝180°，1直角＝90°，1°＝60′，1′＝60″，1′＝(160)°，1″＝(160)′.4．角平分线的概念及性质(1)定义：如果一条射线把一个角分成两个相等的角，那么这条射线叫做这个角的角平分线． (2)性质：角平分线上的点到角两边的距离相等． 警示：到角两边距离相等的点在角平分线上． 5．余角、补角、邻补角(1)余角：A.如果两个角的和为__90°__，那么这两个角互为余角； B ．同角(等角)的余角相等．(2)补角：A.如果两个角的和为__180°__，那么这两个角互为补角； B ．同角(等角)的补角相等．(3)邻补角：A.两个角有一个公共顶点和一条公共边，另一边互为反向延长线的两个角互为邻补角； B ．互为邻补角的两个角的和为180°.分类 锐角 直角 钝角 平角 周角 度数0°<α<90°α＝90°90°<α ＜180°α＝180°α＝360°相交线三线八角(如图)6．同位角有：∠1与__∠5__，∠2与∠6，∠4与∠8，∠3与∠7.7．内错角有：∠2与__∠8__，∠3与∠5.8．同旁内角有：∠3与∠8，∠2与__∠5__．9．对顶角：∠1与∠3为对顶角，∠2与__∠4__为对顶角，∠5与∠7为对顶角，∠6与__∠8__为对顶角．垂线及其性质10．定义：两条直线相交所成的四个角中，如果有一个角是直角，我们就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线．11．基本事实：经过直线上或直线外一点，有且只有一条直线与已知直线垂直．12．性质：直线外一点与直线上各点连接的所有线段中，垂线段最短．13．点到直线的距离：从直线外一点到这条直线的垂线段长度．14．线段垂直平分线：(1)定理：线段垂直平分线上的点到线段两端的距离__相等__．(2)逆定理：到一条线段的两端点的距离相等的点在线段的垂直平分线上．平行线的判定及性质15．定义：在同一平面内，不相交的两条直线叫做平行线．16．两条平行线之间的距离处处相等．17．性质：(1)两直线平行，同位角相等，即∠1＝__∠2__.(2)两直线平行，内错角相等，即∠2＝__∠3__．(3)两直线平行，同旁内角互补，即∠3＋__∠4__＝180°.18．判定：(1)基本事实：经过已知直线外一点，有且只有一条直线和已知直线平行．(2)同位角相等，两直线平行．(3)内错角相等，两直线平行．(4)同旁内角互补，两直线平行．(5)平行于同一条直线的两条直线平行．命题与定理19．命题：判断一件事情的句子叫做命题，命题由题设、结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，命题常写成“如果……那么……”的形式．20．真命题：如果题设成立，那么结论一定成立的命题叫做真命题．21．假命题：题设成立，不能保证结论一定成立的命题叫做假命题．22．定理：有些命题的正确性是用推理证实的，这样的真命题叫做定理，推理过程叫做证明．【方法技巧】利用平行线性质求角度：先观察要求角与已知角的位置关系，再选择合理的角度进行等量代换，因此需要熟练掌握平行线的性质．另外在解题中要注意平角、直角及三角形内角和、三角形内外角关系等知识的运用．,中考重难点突破)补角、余角的计算【例1】(2016湘西中考)一个角的度数是40°，那么它的余角的补角度数是( )A．130°B．140°C．50°D．90°【解析】若两个角的和为90°，则这两个角互余；若两个角的和等于180°，则这两个角互补．依此求出度数．【学生解答】A1．(2016保定博野模拟)将直角三角尺的直角顶点靠在直尺上，且斜边与这根直尺平行，那么，在形成的这个图中与∠α互余的角共有( C)A．4个B．3个C．2个D．1个(第1题图)(第2题图)2．(2016河北沧州八中二模)将一副直角三角板ABC和EDF如图放置(其中∠A＝60°，∠F＝45°)．使点E 落在AC边上，且ED∥BC，则∠CEF的度数为__15°__．平行线的性质与判定【例2】(2016白银中考)如图，AB∥CD，DE⊥CE，∠1＝34°，则∠DCE的度数为( )A．34°B．54°C．66°D．56°【学生解答】D【点拨】此题主要运用平行线的性质：两直线平行，内错角相等(或两直线平行，同旁内角互补)来解．3．(2016盐城中考)如图，点D、E分别在AB、BC上，DE∥AC，AF∥BC，∠1＝70°，则∠2＝__70__°.(第3题图)(第4题图)4．(2016承德二中二模)如图，AB∥CD，∠1＝62°，FG平分∠EFD，则∠2＝__31__°. 5．(2016河北石家庄二十八中一模)如图，AB∥CD，∠1＝130°，则∠2＝__50°__．,中考备考方略)1．(2016长沙中考)下列各图中，∠1和∠2互为余角的是( B),A) ,B),C) ,D) 2．(2016福州中考)如图，直线a，b被直线c所截，∠1与∠2的位置关系是( B)A．同位角B．内错角C．同旁内角D．对顶角3．(2016孝感中考)如图，直线a，b被c所截，若a∥b，∠1＝110°，则∠2等于( A)A．70°B．75°C．80°D．85°(第3题图)(第4题图) 4．(2016陕西中考)如图，AB∥CD，AE平分∠C AB交CD于点E，若∠C＝50°，则∠AED＝( B)A．65°B．115°C．125°D．130°5．(2016龙岩中考)下列命题是假命题的是( A)A．若|a|＝|b|，则a＝bB．两直线平行，同位角相等C．对顶角相等D．若b2－4ac>0，则方程ax2＋bx＋c＝0(a≠0)有两个不等的实数根6．(2016邢台金华中学模拟)直线a，b，c，d的位置如图所示，如果∠1＝58°，∠2＝58°，∠3＝70°，那么∠4等于( C)A．58°B．70°C．110°D．116°(第6题图)(第7题图) 7．(2016廊坊二模)如图直尺EF压在三角板上，∠BAC＝30°，则∠CME＋∠BNF是( B) A．180°B．150°C．135°D．不能确定8．(2016保定二模)如图，直线l1∥l2，点A在直线l1上，以点A为圆心，适当长为半径画弧，分别交直线l1，l2于点B、点C，连接AC，BC，若∠ABC＝54°，则∠1的大小为( B)A．70°B．72°C．74°D．76°(第8题图)(第9题图) 9．(2016邯郸十一中模拟)如图，直线a∥b，一块含60°角的直角三角板ABC(∠A＝60°)按如图所示放置．若∠1＝55°，则∠2的度数为( C)A．105°B．110°C．115°D．120°10．(2016秦皇岛二模)如图，C、D是线段AB上两点，已知图中所有线段的长度都是正整数，且总和为29，则线段AB的长度是( C)A．8 B．9C．8或9 D．无法确定11．(2016沧州九中一模)如图，直线l∥m，等边三角形ABC的顶点B在直线m上，∠1＝25°，∠2的度数为( A)A．35°B．25°C．30°D．45°,(第11题图)),(第12题图))12．(2016毕节中考)如图，直线a∥b，∠1＝85°，∠2＝35°，则∠3＝( C)A．85°B．60°C．50°D．35°13．(2016秦皇岛二模)如图，射线AB，CD分别与直线l相交于点G，点H，若∠1＝∠2，∠C＝65°，则∠A 的度数是__115°__．(第13题图)(第14题图)14．(2016菏泽中考)如图，将一副三角板和一张对边平行的纸条按如图所示方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是__15°__．15．(2016莆田中考)已知直线a∥b，一块直角三角板按如图所示放置，若∠1＝37°，则∠2＝__53°__．(第15题图)(第16题图)16．(2016原创)将一副三角板如图放置，使点A在DE上，BC∥DE，则∠AFC的度数为__75°__．。

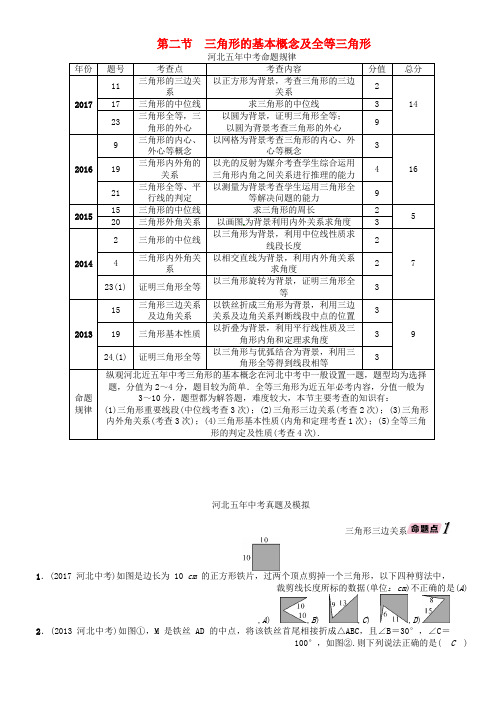
第二节 三角形的基本概念及全等三角形以画图为背景利用内外关系求角度(1)河北五年中考真题及模拟三角形三边关系1．(2017河北中考)如图是边长为10 cm 的正方形铁片，过两个顶点剪掉一个三角形，以下四种剪法中，裁剪线长度所标的数据(单位：cm )不正确的是(A ),A ),B ) ,C ) ,D ) 2．(2013河北中考)如图①，M 是铁丝AD 的中点，将该铁丝首尾相接折成△ABC，且∠B＝30°，∠C ＝100°，如图②.则下列说法正确的是( C )图① 图②A ．点M 在AB 上 B ．点M 在BC 的中点处C ．点M 在BC 上，且距点B 较近，距点C 较远D ．点M 在BC 上，且距点C 较近，距点B 较远3．(2016邢台中考模拟)下列各组数中，能成为一个三角形的三条边长的是( A )A ．2，3，4B ．2，2，4C ．1，2，3D ．1，2，6 4．(2016邯郸中考模拟)三角形的两边长分别为3和6，第三边的长是方程x 2－6x ＋8＝0的一个根，则这个三角形的周长是( D ) A ．2或4 B ．11或13C ．11D ．13 三角形内外角关系5．(2014河北中考)如图，平面上直线a ，b 分别过线段OK 的两端点(数据如图)，则a ，b 相交所成的锐角是( B )A ．20°B ．30°C ．70°D ．80°,(第5题图)) ,(第6题图))6．(2017河北中考模拟)将一副直角三角板按如图所示叠放在一起，则图中∠α的度数是( C )A ．45°B ．60°C ．75°D ．90°7．(2016河北中考)如图，已知∠AOB＝7°，一条光线从点A 出发后射向OB 边．若光线与OB 边垂直，则光线沿原路返回到点A ，此时∠A＝90°－7°＝83°.当∠A<83°时，光线射到OB 边上的点A 1后，经OB 反射到线段AO 上的点A 2，易知∠1＝∠2.若A 1A 2⊥AO ，.°__76__＝∠A 此时，A 原路返回到点A →1A →2A 光线又会沿 …….°__6__的最小值＝∠A 则锐角，A 经若干次反射能沿原路返回到点，发出后A 若光线从点 三角形的四条重要线段8．(2016河北中考)如图为4×4的网格图，A ，B ，C ，D ，O 均在格点上，点O 是( B )A ．△ACD 的外心B ．△ABC 的外心 C ．△ACD 的内心 D ．△ABC 的内心(第8题图)(第9题图)9．(2014河北中考)如图，在△ABC 中，D ，E 分别是边AB ，AC 的中点．若DE ＝2，则BC ＝( C )A ．2B ．3C ．4D ．5。

第六节矩形、菱形、正方形,贵阳五年中考命题规律)年份题型题号考察点考察内容分值总分2021解答18正方形的性质以正方形为背景考察全等三角形的判定，直角三角形的判定10解答22菱形的性质在直角坐标系中，以菱形为背景考察反比例函数、一次函数的有关知识10202021 解答18菱形菱形的性质及判定10102021解答18菱形菱形的性质及判定10102021解答20菱形利用菱形的性质：(1)1010定．命题预测预计2021年中考，特殊的平行四边形内容仍为重点考察内容，且以解答题形式出现，平时训练要加大对性质及判定的训练力度.,贵阳五年中考真题及模拟)菱形的性质及判定(4次)1．(2021贵阳22题10分)如图，在平面直角坐标系中，菱形OBCD的边OB 在x轴上，反比例函数y＝x k(x＞0)的图象经过菱形对角线的交点A，且及边BC交于点F，点A的坐标为(4，2)．(1)求反比例函数的表达式；(2)求点F的坐标．解：(1)∵反比例函数y＝x k的图象经过点A，A点的坐标为(4，2)，∴2＝4k，∴k ＝8.∴反比例函数的表达式为y＝x8；(2)过点A作AM⊥x轴于点M，过点C作CN ⊥x轴于点N，由题意可知，CN＝2AM＝4，ON＝2OM＝8，∴点C的坐标为C(8，4)，设OB＝x，那么BC＝x，BN＝8－x，在Rt△CNB中，x2－(8－x)2＝42，解得x＝5，∴点B的坐标为B(5，0)，设直线BC的函数表达式为y＝k1x＋b，直线BC过点B(5，0)，C(8，4)，∴8k1＋b＝4，5k1＋b＝0，解得：，20∴直线BC的表达式为yx2＝－1，∵点F在第一象限，∴点F ＝34x－320，根据题意得方程组，8解此方程组得：，4y2＝－8，的坐标为F(6，34)．2．(2021 贵阳18题10分)如图，在Rt△ABC中，∠ACB＝90°，D为AB 的中点，且AE∥CD，CE∥AB.(1)证明：四边形ADCE是菱形；(2)假设∠B＝60°，BC＝6，求菱形ADCE的高．(计算结果保存根号)解：(1)∵AE∥CD，CE∥AB，∴四边形ADCE是平行四边形，又∵∠ACB＝90°，D是AB的中点，∴CD＝BD＝AD，∴平行四边形ADCE是菱形；(2)如图，过点D作DF⊥CE，垂足为点F，那么DF即为菱形ADCE的高，∵∠B＝60°，CD＝BD，∴△BCD是等边三角形．∵CE∥AB，∴∠BCE＝120°，∴∠DCE＝60°，又∵CD＝BC＝6，∴在Rt△CDF中，DF＝3.3．(2021贵阳18题10分)如图，在Rt△ABC中，∠ACB＝90°，D，E分别为AB，AC边上的中点，连接DE，将△ADE绕点E旋转180°得到△CFE，连接AF.(1)求证：四边形ADCF是菱形；(2)假设BC＝8，AC＝6，求四边形ABCF的周长．解：(1)∵将△ADE绕点E旋转180°得到△CFE.∴AE＝CE，DE＝FE，∴四边形ADCF为平行四边形．∵点D，E是AB及AC的中点，∴DE是△ABC的中位线，∴DE∥BC，∵∠ACB＝90°即BC⊥AC，∴DF⊥AC，∴平行四边形ADCF为菱形；(2)∵在Rt△ABC中，BC＝8，AC＝6，∴AB＝10.∵点D是AB 边上的中点，∴AD＝5.∵四边形ADCF为菱形，∴AF＝FC＝AD＝5，∴C四边形＝8＋10＋5＋5＝28.ABCF4．(2021贵阳20题10分)：如图，在菱形ABCD中，F是BC上任意一点，连接AF交对角线BD于点E，连接EC.(1)求证：AE＝EC；(2)当∠ABC＝60°，∠CEF＝60°时，点F在线段BC上的什么位置？说明理由．解：(1)连接AC，∵四边形ABCD为菱形，∴BD垂直平分AC，∴AE＝EC；(2)点F是线段BC的中点，理由如下：易得△ABC是等边三角形，∴∠BAC＝60°，∵AE＝EC，∠CEF＝60°，∴∠EAC＝21∠BAC＝30°，∴AF是△ABC 的角平分线，∵AF交BC于点F，∴AF是△ABC边BC上的中线，∴点F是线段BC的中点．正方形的性质(2次)5．(2021贵阳模拟卷②15题)如图，在平面直角坐标系中，边长不等的正方形依次排列，每个正方形都有一个顶点落在函数y＝x的图象上，从左向右第3个正方形中的一个顶点A的坐标为(8，4)，阴影三角形局部的面积从左向右依次记为S1，S2，S3，……，S n，那么S n的值为__24n－5__．(用含n的代数式表示，n为正整数) 6．(2021贵阳21题10分)如图，在正方形ABCD中，等边三角形AEF的顶点E、F分别在BC与CD上．(1)求证：CE＝CF；(2)假设等边三角形AEF的边长为2，求正方形ABCD的周长．解：(1)易证△ABE≌△ADF，∴BE＝DF，又BC＝DC，∴BC－BE＝DC－DF，∴CE＝CF；(2)连接AC，交EF于G点，易得AC⊥EF，EC＝，设BE＝x，那么AB＝x＋，在Rt△ABE中，(x＋)2＋x2＝4，∴x＝26，∴AB＝26＋＝26，∴正方形的周长为2＋2.7．(2021 贵阳适应性考试)如图，E，F是菱形ABCD对角线AC上的两点，且AE＝CF.(1)求证：四边形BEDF是菱形；(2)假设∠DAB＝60°，AD＝6，AE＝DE，求菱形BEDF的周长．解：(1)∵菱形ABCD，∴AB＝AD，对角线AC平分∠BAD，∴∠BAE＝∠DAE，又∵AE＝AE，∴△ABE≌△ADE，∴BE＝ED.连接BD交AC于点O，那么OD＝OB，OA＝OC，∵AE＝CF，∴OA－AE＝OC－CF，∴OE＝OF，∴四边形BEDF为平行四边形，∴▱BEDF为菱形；(2)在菱形ABCD中，连接BD交于AC于O点，∴DB⊥AC，又∵∠DAB＝60°，∴∠DAE＝30°，∠ADB＝60°，∵AD＝6，∴在Rt△ADO中，DO＝21AD＝3，∵AE＝ED，∴∠DAE＝∠ADE，∠ADE＝∠EDO＝30°，在Rt△DEO中，可求得DE＝2，∴菱形BEDF 的周长为8.,中考考点清单)矩形的性质及判定1．定义：把有一个角是直角的平行四边形叫做矩形．如图(1)．2．性质文字描述字母表示[参考图(1)](1)对边平行且相等AD綊BC，AB綊CD(2)四个内角都是直角__∠DAB__＝∠ABC＝∠BCD ＝∠CDA＝90°(3)两条对角线相等且互相平分AC＝__BD__，OA＝OC＝OB＝OD(4)矩形既是中心对称图形，也是轴对称图形3.判定文字描述字母表示[参考图(1)](1)有一个角是直角的平行四边形是矩形假设四边形ABCD是平行四边形，且∠BAD＝90°，那么四边形ABCD是矩形(2)有三个角是直角的四边形是矩形假设∠BAD＝∠ABC＝∠BCD＝90°，那么四边形ABCD是矩形(3)对角线相等的平行四边形是矩形假设AC＝__BD__，且四边形ABCD是平行四边形，那么四边形ABCD是矩形菱形的性质及判定(高频考点)4．定义：把有一组邻边相等的平行四边形叫做菱形．如图(2) 5．性质文字描述字母表示[参考图(2)](1)菱形的四条边都相等AB＝__BC__＝CD＝DA(2)对角相等∠DAB＝∠DCB，∠ADC＝__∠ABC__(3)两条对角线互相垂直，且每条对角线平分一组对角__AC__⊥BD，∠DAC＝∠CAB ＝∠DCA＝∠ACB，∠ADB＝∠BDC＝∠ABD＝∠DBC(4)菱形既是中心对称图形，也是轴对称图形6．判定文字描述字母表示[参考图(2)](1)有一组邻边相等的平行四边形是菱形假设四边形ABCD是平行四边形，且AD＝AB，那么四边形ABCD是菱形(2)四条边相等的四边形是菱形假设AB＝BC＝CD＝DA，那么四边形ABCD是菱形(3)两条对角线互相垂直的平行四边形是菱形假设AC⊥BD，且四边形ABCD 是平行四边形，那么四边形ABCD是菱形正方形的性质及判定7．定义：有一组邻边相等且有一个角是直角的平行四边形叫做正方形．如图(3)8．性质文字描述字母表示[参考图(3)](1)四条边都相等即AB＝BC＝CD＝DA(2)四个角都是90°即∠ABC＝∠ADC＝∠BCD＝∠BAD＝90°(3)对角线互相垂直平分且相等即AC⊥__BD__，OA＝OC＝OD＝OB(4)对角线平分一组对角∠DAC＝∠CAB＝∠DCA＝∠ACB＝∠ADB＝∠BDC＝∠ABD＝∠DBC＝45°(5)正方形既是中心对称图形，也是轴对称图形9.判定文字描述字母表示[参考图(3)](1)一组邻边相等且有一个角是直角的平行四边形叫做正方形假设四边形ABCD是平行四边形，且AB＝BC，∠ADC＝90°，那么四边形ABCD是正方形(2)有一个角是直角的__菱形__是正方形假设∠ABC＝90°且四边形ABCD是菱形，那么四边形ABCD是正方形(3)有一组邻边相等的矩形是正方形假设AB＝BC，且四边形ABCD 是矩形，那么四边形ABCD是正方形(4)对角线互相垂直平分且相等的四边形是正方形假设四边形ABCD中，AC⊥BD，AC平分BD，BD平分AC，AC＝BD，那么四边形ABCD是正方形,中考重难点突破)矩形的有关计算【例1】(2021天津中考)如图，把一张矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′，AB′，DC相交于点E，那么以下结论一定正确的选项是( ) A．∠DAB′＝∠CAB′B．∠ACD＝∠B′CDC．AD＝AED．AE＝CE【解析】由折叠的性质得：∠CAB′＝∠∵AB∥CD，∴∠ACD＝∠CAB＝∠CAB′，∴AE＝CE.【学生解答】D1．(2021海南中考)如图，矩形ABCD的顶点A，C分别在直线a，b上，且a ∥b，∠1＝60°，那么∠2的度数为( C )A．30°B．45°C．60°D．75°,(第1题图)) ,(第2题图))2．(2021南充中考)如图，对折矩形纸片ABCD，使AB及DC重合得到折痕EF，将纸片展平；再一次折叠，使点D落到EF上点G处，并使折痕经过点A，展开纸片后∠DAG的大小为( C )A．30°B．45°C．60°D．75°3．(2021巴中中考)如图，延长矩形ABCD的边BC至点E，使CE＝BD，连接AE，如果∠ADB＝30°，那么∠E＝__15__°.菱形的性质及判定【例2】(2021南充中考)如图，菱形ABCD的周长是8 cm，AB的长是________cm.【解析】菱形的四边形相等，故AB＝8÷4＝2(cm)．【学生解答】24．(2021无锡中考)以下性质中，菱形具有而矩形不一定具有的是( C )A．对角线相等B．对角线互相平分C．对角线互相垂直D．邻边互相垂直5．(2021雅安中考)如图，四边形ABCD的四边相等，且面积为120 cm2，对角线AC＝24 cm，那么四边形ABCD的周长为( A )A．52 cm B．40 cmC．39 cm D．26 cm6．(2021遵义中考)在▱ABCD中，，使▱ABCD成为菱形，以下给出的条件不正确的选项是( C )A．AB＝AD B．AC⊥BDC．AC＝BD D．∠BAC＝∠DAC7．(2021苏州中考)如图，在菱形ABCD中，对角线AC，BD相交于点O，过点D作对角线BD的垂线交BA的延长线于点E.(1)证明：四边形ACDE是平行四边形；(2)AC＝8，BD＝6，求△ADE的周长．解：(1)∵四边形ABCD是菱形，∴AB∥CD，AC⊥BD，∴AE∥CD，∠AOB ＝90°.又∵DE⊥BD，即∠EDB＝90°，∴∠AOB＝∠EDB，∴DE∥AC，∴四边形ACDE是平行四边形；(2)∵∵四边形ACDE是平行四边形，∴AE＝CD＝5，DE＝AC＝8，∴△ADE的周长为AD＋AE＋DE＝5＋5＋8＝18.正方形的性质及判定【例3】(2021广东中考)如图，正方形ABCD的面积为1，那么以相邻两边中点的连线EF为边的正方形EFGH的周长为( )A. B．2C.＋1 D．2＋1【解析】由题意可知，正方形ABCD的边长为1，那么CE＝CF＝21.由勾股定理，得EF＝＝）21＝22，故正方形EFGH的周长为2.【学生解答】B8．(2021益阳中考)以下判断错误的选项是( D )A．两组对边分别相等的四边形是平行四边形B．四个内角都相等的四边形是矩形C．四条边都相等的四边形是菱形D．两条对角线垂直且平分的四边形是正方形9．(2021陕西中考)如图，在正方形ABCD中，连接BD，点O是BD的中点，假设M，N是AD上的两点，连接MO，NO，并分别延长交边BC于M′，N′两点，那么图中全等三角形共有( C )A．2对B．3对C．4对D．5对,(第9题图)) ,(第10题图))10．(2021西宁中考)如图，正方形ABCD的边长为3，E，F分别是AB，BC 边上的点，且∠EDF＝45°.将△DAE绕点D逆时针旋转90°，得到△DCM.假设AE＝1，那么FM的长为__25__．。

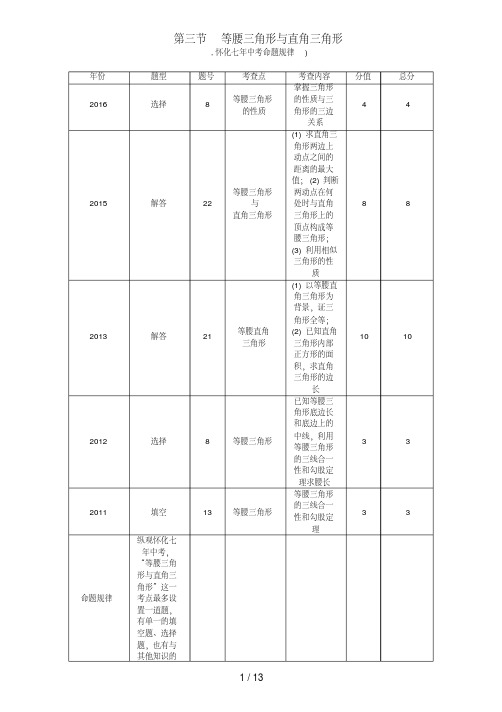
第二节三角形的基本概念及全等三角形,青海五年中考命题规律)全等三角形式出,青海五年中考真题)三角形的边角关系1．(2015青海中考)已知三角形两边的长分别是4和10，则此三角形第三边的长可能是( C)A．5 B．6 C．12 D．162．(2016西宁中考)下列每组数分别是三根小木棒的长度，用它们能摆动成三角形的是( D)A．3 cm、4 cm、8 cm B．8 cm、7 cm、15 cmC．5 cm、5 cm、11 cm D．13 cm、12 cm、20 cm3．(2014西宁中考)下列线段能构成三角形的是( B)A．2，2，4 B．3，4，5 C．1，2，3 D．2，3，64．(2017青海中考)如图，在△ABC中，∠ABC和∠ACB的角平分线相交于点O，若∠A＝50°，则∠BOC＝__115°__.(第4题图)(第5题图)5．(2016青海中考)如图，已知∠CAE是△ABC的外角，AD∥BC，且AD是∠EAC的平分线，若∠B＝71°，则∠BAC＝__38°__．三角形的四条重要线段6．(2013西宁中考)如果等边三角形的边长为4，那么等边三角形的中位线长为( A)A．2 B．4 C．6 D．87．(2016西宁中考)如图，已知直角梯形ABCD的一条对角线把梯形分为一个直角三角形和一个以BC为底的等腰三角形．若梯形上底为5，则连接△DBC的两腰中点的线段的长为__5__．全等三角形8．(2013西宁中考)使两个直角三角形全等的条件是( D)A．一锐角对应相等B．两锐角对应相等C．一条边对应相等D．两条边对应相等9.(2015青海中考)如图，点B，F，C，E在同一直线上，BF＝CE，AB∥DE，请添加一个条件，使△ABC≌△DEF，这个添加的条件可以是__AB＝DE或∠A＝∠D或∠ACB＝∠DFE或AC∥FD__．(只需写一个，不添加辅助线)(第9题图)(第10题图)10．(2014青海中考)如图，已知∠C＝∠D，∠CAB＝∠DBA，AD交BC于点O，请写出图中一组相等的线段__BC＝AD或AC＝BD或OA＝OB或OC＝OD__．11．(2013青海中考)如图，BC＝EC，∠1＝∠2，添加一个适当的条件，使△ABC≌△DEC，则需添加的条件是__答案不唯一，如∠A＝∠D__．(不添加任何辅助线)12．(2014青海中考)如图，▱ABCD中，点E在边AB上，点F在AB的延长线上，且AE＝BF.求证：∠ADE＝∠BCF.证明：∵四边形ABCD是平行四边形，∴AD＝BC且AD∥BC，∴∠DAE ＝∠CBF. 又∵AE＝BF ，∴△DAE ≌△CBF(SAS )， ∴∠ADE ＝∠BCF.13．(2014西宁中考)课间，小明拿着老师的等腰直角三角板玩，不小心掉到两墙之间，如图所示． (1)求证：△ADC≌△CEB；(2)从三角板的刻度可知AC ＝25 cm ，请你帮小明求出砌墙砖块的厚度a 的大小．(每块砖的厚度相等)解：(1)由题意得：AC ＝BC ，∠ACB ＝90°，AD ⊥DE ，BE ⊥DE ，∴∠ADC ＝∠CEB＝90°，∴∠ACD ＋∠BCE＝90°，∠ACD ＋∠DAC＝90°，∴∠BCE ＝∠CAD.在△ADC 和△CEB 中，⎩⎪⎨⎪⎧∠ADC＝∠CEB，∠DAC＝∠ECB，AC ＝CB ，∴△ADC ≌△CEB(AAS )； (2)由题意得：AD ＝4a ，BE ＝3a ， 由(1)得△ADC≌△CEB，∴DC ＝BE ＝3a. 在Rt △ADC 中，AD 2＋DC 2＝AC 2， ∴(4a)2＋(3a)2＝252，即a 2＝25. ∵a ＞0，∴a ＝5.答：砌墙砖块的厚度a 为5 cm .,中考考点清单)三角形分类及三边关系1．三角形分类 (1)按角分类(2)按边分类2．三边关系：三角形任意两边之和__大于__第三边，任意两边之差小于第三边，如图，__a ＋b__>c ，|a －b|<__c__.3.判断几条线段能否构成三角形：运用三角形三边关系判定三条线段能否构成三角形，并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度，即可判断这三条线段能构成一个三角形．三角形内角和定理及内外角关系4．内角和定理：三角形的内角和等于__180°__．5．内外角关系：三角形的一个外角__等于__与它不相邻的两个内角之和．三角形的一个外角大于任何一个和它不相邻的内角．三角形中的四条重要线段全等三角形及其性质6．定义能完全重合的两个三角形叫做全等三角形．7．性质(1)全等三角形的对应边__相等__，对应角__相等__；(2)全等三角形的对应线段(角平分线、中线、高线、中位线)相等，周长__相等__，面积__相等__．全等三角形的判定8．三角形全等的判定∠B1【方法技巧】证明三角形全等的思路判定三角形全等⎩⎪⎪⎨⎪⎪⎧已知两边⎩⎪⎨⎪⎧找夹角→SAS 找直角→HL 或SAS找另一边→SSS已知一边和一角⎩⎪⎨⎪⎧边为角的对边→找任一角→AAS 边为角的邻边⎩⎪⎨⎪⎧找夹角的另一边→SAS 找夹边的另一角→ASA找边的对角→AAS 已知两角⎩⎪⎨⎪⎧找夹边→ASA 找任一边→AAS,中考重难点突破)三角形三边关系【例1】一个三角形的两边长为2和6，第三边为偶数，则这个三角形的周长为( )A ．10B ．12C ．14 D ．16【解析】根据三角形三边关系：两边之和大于第三边，两边之差小于第三边，求出第三边的取值范围，再根据第三边为偶数，求出第三边的长度，从而可求出三角形周长．【答案】C1．(2017舟山中考)长度分别为2，7，x 的三条线段能组成一个三角形，x 的值可以是( C )A ．4B ．5C ．6D ．92．(玉林中考)在等腰△ABC 中，A B ＝AC ，其周长为20 m ，则AB 边的取值范围是( B )A ．1 cm ＜AB ＜4 cm B ．5 cm ＜AB ＜10 cmC ．4 cm ＜AB ＜8 cmD ．4 cm ＜AB ＜10 cm三角形的内角与外角关系【例2】(2018中考预测)如图，CD 是△ABC 外角∠ACE 的平分线，AB∥CD ，∠A ＝50°，则∠B 的大小是( )A ．50°B ．60°C ．40°D ．30°【解析】∵AB∥CD，∴∠A ＝∠ACD＝50°，又∵CD 是△ABC 外角∠ACE 的平分线，∴∠ACD ＝∠DCE＝50°，∴∠ACE ＝2∠ACD＝100°，由三角形内外角关系可得∠B＋∠A＝∠ACE，∴∠B ＝∠ACE －∠A ＝100°－50°＝50°.【答案】A3．(丽水中考)如图，在△ABC 中，∠A ＝63°，直线MN∥BC，且分别与AB ，AC 相交于点D ，E ，若∠AEN＝133°，则∠B 的度数为__70°__．(第3题图)(第4题图)4．(2017郴州中考)小明把一副45°，30°的直角三角板如图摆放，其中∠C＝∠F＝90°，∠A ＝45°，∠D ＝30°，则∠α＋∠β等于( B )A ．180°B ．210°C ．360°D ．270°三角形中重要线段的应用【例3】在△ABC 中，D 为AB 的中点，E 为AC 上一点，CE ＝13AC ，BE ，CD 交于点O ，BE ＝5 cm ，则OE ＝________cm .(例3题图)(例3题解图)【解析】如解图，过D 作DF∥BE，那么DF 就是三角形ABE 的中位线，∴DF ＝12BE ，AF ＝EF ，又∵CE＝13AC ，∴CE ＝EF ，∴OE 就是三角形CDF 的中位线，∵OE ＝12DF ＝14BE ＝1.25 cm .【答案】1.255．(2017遵义中考)如图，△ABC 的面积是12，点D ，E ，F ，G 分别是BC ，AD ，BE ，CE 的中点，则△AFG 的面积是( A )A ．4.5B ．5C ．5.5D ．6(第5题图)(第7题图)6．(内江中考)已知等边三角形的边长为3，点P 为等边三角形内任意一点，则点P 到三边的距离之和为( B )A .32 B .332 C .32D ．不能确定 7．(永州中考)如图，点D ，E 分别在线段AB ，AC 上，CD 与BE 相交于O 点，已知AB ＝AC ，现添加以下的哪个条件仍不能判定△ABE≌△ACD( D )A ．∠B ＝∠C B ．AD ＝AE C ．BD ＝CE D ．BE ＝CD全等三角形的证明及性质【例4】如图，已知点D 为等腰Rt △ABC 内一点，∠CAD ＝∠CBD＝15°，E 为AD 延长线上的一点，且CE ＝CA.若点M 在DE 上，且DC ＝DM ，试探究线段ME 与BD 的数量关系，并说明理由．【解析】连接MC ，先证△BDC≌△ADC，再证△ADC≌△EMC.【答案】解：如图，连接MC.在等腰Rt △ABC 中，∵∠CAD ＝∠CBD＝15°，∴∠BAD ＝∠ABD＝45°－15°＝30°，∴BD ＝AD.又AC ＝B C ，∴△BDC ≌△ADC(SSS )，∴∠DCA ＝∠DCB＝45°，∠EDC ＝∠DAC＋∠DCA＝15°＋45°＝60°.∵DC ＝DM ，∴△MDC 是等边三角形，即CM ＝CD.又∵∠EMC＝180°－∠DMC＝180°－60°＝120°，∠ADC ＝180°－∠MDC＝180°－60°＝120°，∴∠EMC ＝∠ADC.又∵CE＝CA ，∴∠DAC ＝∠CEM＝15°，∴△ADC ≌△EMC(AAS )，∴ME ＝AD ＝DB ，∴ME ＝BD.8．(2017孝感中考)如图，已知AB ＝CD ，AE ⊥BD ，CF ⊥BD ，垂足分别为E ，F ，BF ＝DE ，求证：AB ∥CD.解：∵AE⊥BD，CF ⊥BD ，∴∠AEB ＝∠CFD＝90°.∵DE ＝BF ，∴DE ＋EF ＝BF ＋EF ，即BE ＝DF.在Rt △AEB 和Rt△CFD 中，⎩⎪⎨⎪⎧AB ＝CD ，BE ＝DF ，∴Rt △AEB ≌Rt △CFD(HL )，∴∠B ＝∠D，∴AB ∥CD.9．(2017怀化中考)如图，四边形ABCD 是正方形，△EBC 是等边三角形． (1)求证：△ABE≌△DCE； (2)求∠AED 的度数．解：(1)∵四边形ABCD 为正方形，△BCE 为等边三角形，∴AB ＝BE ＝CE ＝CD ，∴∠ABE ＝∠DCE＝30°.由⎩⎪⎨⎪⎧AB ＝DC ，∠ABE ＝∠DCE，EB ＝EC ，可知△ABE≌△DCE(SAS )； (2)由(1)知AE ＝DE ，即△AED 为等腰三角形．又∵AB＝BC ＝BE ，∴∠BAE ＝180°－∠ABE2＝75°，则∠DAE＝90°－∠BAE＝15°，∴∠AED ＝180°－2∠DAE ＝150°.10．如图，在△ABC 中，∠ACB ＝90°，AC ＝BC ，BE ⊥CE 于点E ，AD ⊥CE 于点D. (1)求证：△BEC≌△CDA；(2)试判断BE ，DE ，AD 三条线段之间的关系．证明：(1)∵∠ACB＝90°，∴∠BCE ＋∠ACD＝90°.∵BE ⊥CE ，AD ⊥CE ，∴∠E ＝∠CDA＝90°.又∵∠BCE＋∠CBE＝90°，∴∠ACD ＝∠CBE.又AC ＝BC ，∴△BEC ≌△CDA(AAS )；(2)由(1)知CE ＝AD.∵CD＋DE ＝CE ，∴CD ＋DE ＝AD.又∵BE＝CD ，∴BE ＋DE ＝AD.11．(2017连云港中考)如图，已知等腰三角形ABC 中，AB ＝AC ，点D ，E 分别在边AB ，AC 上，且AD ＝AE ，连接BE ，CD ，交于点F.(1)判断∠ABE 与∠ACD 的数量关系，并说明理由； (2)求证：过点A ，F 的直线垂直平分线段BC.解：(1)∠ABE＝∠ACD，∵AB ＝AC ，∠BAE ＝∠CAD ，AE ＝AD ，∴△ABE ≌△ACD ，∴∠ABE ＝∠ACD；(2)∵AB＝AC ，∴∠ABC ＝∠ACB，由(1)可知∠ABE＝∠ACD，∴∠FBC ＝∠FCB，∴FB ＝FC.又∵AB＝AC ，∴点A ，F 均在线段BC 的垂直平分线上，即直线AF 垂直平分线段BC.12．(2017齐齐哈尔中考)如图，在△ABC 中，AD ⊥BC 于点D ，BD ＝AD ，DG ＝DC ，点E ，F 分别是BG ，AC 的中点．(1)求证：DE ＝DF ，DE ⊥DF ；(2)连接EF ，若AC ＝10，求EF 的长．解：(1)∵AD⊥BC，∴∠ADB ＝∠ADC＝90°.在△BDG 和△ADC 中，⎩⎪⎨⎪⎧BD ＝AD ，∠BDG ＝∠ADC，DG ＝DC ，∴△BDG ≌△ADC ，∴BG ＝AC ，∠BGD ＝∠C.∵∠ADB ＝∠ADC＝90°，E ，F 分别是BG ，AC 的中点，∴DE ＝12BG ＝EG ，DF ＝12AC ＝AF.∴DE＝DF ，∠EDG ＝∠EGD＝∠C，∠FDA ＝∠FAD，∴∠EDG ＋∠FDA＝90°，∴DE ⊥DF ；(2)∵AC＝10，∴DE ＝DF ＝5，由勾股定理，得EF ＝DE 2＋DF 2＝5 2.。

第二节三角形的基本概念及全等三角形,怀化七年中考命题规律)年份题型题号考查点考查内容分值总分2016解答17 全等三角形全等三角形的判定及其性质8 82015解答17 三角形中位线利用三角形的中位线的性质得条件，证三角形全等8 82014选择 5 全等三角形以等腰梯形为背景，判断三角形全等3填空15 三角形内外角关系利用三角形的内外角关系求角3 62013选择 5 三角形中位线以测量池塘为背景，利用三角形中位线的性质得到两点间的距离3 32012解答19 全等三角形以等腰梯形为背景证三角形全等10填空11 三角形中位线以平行四边形为背景，利用三角形中位线的性质求线段的长度3 132011选择 2 三角形内外角的关系利用三角形的外角与内角的关系比较大小3 3命题规律纵观怀化七年中考，“三角形的基本概念及全等三角形”这一考点除2010年没考查外，其余各年都有考查，基本概念考查层次偏低，全等三角形考查中等，其中，三角形内外角关系考查2次，三角形中位线考查3次，全等三角形考查3次．命题预测预计2017年怀化中考会以三角形中的重要线段，三角形的内外角关系为主要考查对象，全等三角形的判定和性质也会在解答题中考查.,怀化七年中考真题及模拟)三角形的内外角关系(2次)1．(2011怀化中考)如图所示，∠A，∠1，∠2的大小关系是( B) A．∠A>∠1>∠2 B．∠2>∠1>∠AC．∠A>∠2>∠1 D．∠2>∠A>∠1(第1题图)(第2题图)2．(2014怀化中考)如图，在△ABC中，∠A＝30°，∠B＝50°，延长BC到D，则∠ACD＝__80°__．三角形的中位线(3次)3．(2013怀化中考)如图，为测量池塘边A，B两点的距离，小明在池塘的一侧选取一点O，测得OA，OB的中点分别是点D，E，且DE＝14 m，则A，B间的距离是( C)A．18 m B．24 m C．28 m D．30 m(第3题图)(第4题图)4．(2012怀化中考)如图，在▱ABCD中，AD＝8，点E，F分别是BD，CD的中点，则EF＝__4__．全等三角形(3次)5．(2014怀化中考)如图，已知等腰梯形ABCD中，AD∥BC，AB＝DC，AC与BD相交于点O，则下列判断不正确的是( B)A．△ABC≌△DCB B．△AOD≌△COBC．△ABO≌△DCO D．△ADB≌△DAC(第5题图)(第6题图)6．(2016怀化二模)如图，OP是∠AOB的平分线，点C，D分别在角的两边OA，OB上．添加下列条件，不能判定△POC≌△POD的选项是( D)A．PC⊥OA，PD⊥OB B．OC＝ODC．∠OPC＝∠OPD D．PC＝PD7．(2016怀化学业考试指导)一个等腰三角形的两边长分别为2和5，则它的周长为( C)A．7 B．9 C．12 D．9或128．(2016鹤城模拟)三角形的两边长分别为3和6，第三边的长是方程x2－6x＋8＝0的一个根，则这个三角形的周长是( D)A．2或4 B．11或13C．11 D．139．(2016芷江模拟)在△ABC中，∠ABC＝30°，AB边长为10，AC边的长度可以在3、5、7、9、11中取值，满足这些条件的互不全等的三角形的个数是( D)A．3个B．4个C．5个D．6个10．(2016怀化考试说明)如图，D为△ABC内一点，CD平分∠ACB，BE⊥CD，垂足为D，交AC于点E，∠A＝∠ABE，若AC＝5，B C＝3，则BD的长为( D)A．2.5 B．1.5 C．2 D．111．(2012怀化中考)如图，在等腰梯形ABCD中，点E为底边BC的中点，连接AE，DE.求证：AE＝DE.证明：∵四边形ABCD 为等腰梯形，∴AB ＝DC ，∠B ＝∠C，∵E 为BC 的中点，∴BE ＝CE ，∴△ABE ≌△DCE(SAS )，∴AE ＝DE.12．(2016怀化中考)如图，已知AD ＝BC ，AC ＝BD. (1)求证：△ADB≌△BCA；(2)OA 与OB 相等吗？若相等，请说明理由．证明：(1)在△ADB 和△BCA 中，⎩⎪⎨⎪⎧AD ＝BC ，AC ＝BD ，AB ＝BA ，∴△ADB ≌△BCA(SSS )；(2)OA ＝OB.理由如下：∵△ADB≌△BCA，∴∠DBA ＝∠CAB，即∠OAB＝∠OBA，∴OA ＝OB.13．(2016怀化一模)如图，点E ，F 在BC 上，BE ＝C F ，∠A ＝∠D，∠B ＝∠C，求证：AB ＝DC.证明：∵BE＝CF ，∴BF ＝CE ，又∵∠A＝∠D，∠B ＝∠C，∴△ABF ≌△DCE ，∴AB ＝DC.14．(2016洪江模拟)已知△ABN 和△ACM 的位置如图所示，AB ＝AC ，AD ＝AE ，∠1＝∠2. 求证：(1)BD ＝CE ；(2)∠M＝∠N.证明：(1)∵在△ABD 和△A CE 中，⎩⎪⎨⎪⎧AB ＝AC ，∠1＝∠2，AD ＝AE ，∴△ABD ≌△ACE ，∴BD ＝CE ；(2)∵△ABD≌△ACE，∴∠ADB ＝∠AEC.又∵∠MDO＝∠ADB，∠NEO ＝∠AEC，∴∠MDO ＝∠NEO.∵∠MOD＝∠NOE，∴180°－∠MDO－∠MOD＝180°－∠NEO－∠NOE，∴∠M ＝∠N.考点清单)三角形分类及三边关系1．三角形分类 (1)按角分类锐角三角形直角三角形 钝角三角形两条边相等的三角形 三边相等的三角形 三边互不相等的三角形__等腰__三角形__等边__三角形不等边三角形2．三边关系：三角形任意两边之和__大于__第三边，任意两边之差小于第三边，如图，__a＋b__>c，|a－b|<__c__．3．判断几条线段能否构成三角形：运用三角形三边关系判定三条线段能否构成三角形，并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判断这三条线段能构成一个三角形．三角形内角和定理及内外角关系4．内角和定理：三角形的内角和等于__180°__．5．内外角关系：三角形的一个外角__等于__与它不相邻的两个内角之和．三角形的一个外角大于任何一个和它不相邻的内角．三角形中的四条重要线段四线定义性质图形中线连接一个顶点与它对边中点的线段BD＝DC高线从三角形一个顶点到它对边所在直线的垂线段AD⊥BC，即∠ADB＝∠ADC＝90°续表角平分线一个内角的平分线与这个角的对边相交，顶点与交点之间的线段∠1＝∠2中位线连接三角形两边中点的线段DE∥BC且DE＝12BC全等三角形及其性质6．定义：能完全重合的两个三角形叫做全等三角形．7．性质：(1)全等三角形的对应边__相等__，对应角__相等__．(2)全等三角形的对应线段(角平分线、中线、高线、中位线)相等，对应__周长__相等，对应面积__相等__．全等三角形的判定8类型图形已知条件是否全等形成结论一般三角形的判定A1B1＝A2B2，B1C1＝B2C2，A1C1＝A2C2是__SSS__∠B1＝∠B2，B1C1＝B2C2，∠C1＝∠C2是ASA∠B1＝∠B2，∠C1＝∠C2，A1C1＝A2C2是AASA1B1＝A2B2，是__SAS__∠B 1＝∠B2，B1C1＝B2C2续表直角三角形的判定A1B1＝A2B2，A1C1＝A2C2，是__HL__ 【方法技巧】证明三角形全等的思路判定三角形全等⎩⎪⎪⎨⎪⎪⎧已知两边⎩⎪⎨⎪⎧找夹角→SAS找直角→HL或SAS找另一边→SSS已知一边和一角⎩⎪⎨⎪⎧边为角的对边→找任一角→AAS边为角的邻边⎩⎪⎨⎪⎧找夹角的另一边→SAS找夹边的另一角→ASA找边的对角→AAS已知两角⎩⎪⎨⎪⎧找夹边→ASA找任一边→AAS,中考重难点突破)三角形三边关系【例1】(2015洪江模拟)如图，用四个螺丝将四条不可弯曲的木条围成一个木框，不计螺丝大小，其中相邻两螺丝的距离依次为2、3、4、6，且相邻两木条的夹角均可调整．若调整木条的夹角时不破坏此木框，则任意两个螺丝间距离的最大值为( )A．5 B．6 C．7 D．10【解析】已知4条木棍的四边长为2、3、4、6；①选2＋3、4、6作为三角形，则三边长为5、4、6；5－4<6<5＋4，能构成三角形，此时两个螺丝间的最大距离为6；②选3＋4、6、2作为三角形，则三边长为2、7、6；6－2<7<6＋2，能构成三角形，此时两个螺丝间的最大距离为7；③选4＋6、2、3作为三角形，则三边长为10、2、3；2＋3<10，不能构成三角形，此种情况不成立；④选6＋2、3、4作为三角形，则三边长为8、3、4；而3＋4<8，不能构成三角形，此种情况不成立．综上所述，任意两个螺丝间距离的最大值为7.【学生解答】C1．(2016岳阳中考)下列长度的三根小木棒能构成三角形的是( D ) A ．2 cm ，3 cm ，5 cm B ．7 cm ，4 cm ，2 cm C ．3 cm ，4 cm ，8 cm D ．3 cm ，3 cm ，4 cm 三角形的内角和外角关系【例2】(2016原创)如图，CD 是△ABC 外角∠ACE 的平分线，AB ∥CD ，∠A ＝50°，则∠B 的大小是( ) A ．50° B ．60° C ．40° D ．30°【解析】∵AB∥CD，∴∠A ＝∠ACD＝50°，又∵CD 是△ABC 外角∠ACE 的平分线，∴∠ACD ＝∠DCE＝50°，∴∠ACE ＝2∠ACD＝100°，由三角形内外角关系可得∠B ＋∠A＝∠ACE，∴∠B ＝∠ACE －∠A ＝100°－50°＝50°.【学生解答】A2．(2016乐山中考)如图，CE 是△ABC 的外角∠ACD 的平分线，若∠B＝35°，∠ACE ＝60°，则∠A＝( C ) A ．35° B ．95° C ．85° D ．75°三角形中重要线段的应用【例3】在△ABC 中，D 为AB 的中点，E 为AC 上一点，CE ＝13AC ，BE ，CD 交于点O ，BE ＝5 cm ，则OE ＝________cm .(例3题图)(例3题解图)【解析】如解图，过D 作DF∥BE，那么DF 就是三角形ABE 的中位线，∴DF ＝12BE ，AF ＝EF ，又∵CE ＝13AC ，∴CE ＝EF ，∴OE 就是三角形CDF 的中位线，∴OE ＝12DF ＝14BE ＝1.25 cm .【学生解答】1.253．(2016枣庄中考)如图，△ABC 的面积为6，AC ＝3，现将△ABC 沿AB 所在直线翻折，使点C 落在直线AD 上的C′处，P 为直线AD 上的一点，则线段BP 的长不可能是( A )A ．3B ．4C ．5.5D ．10全等三角形的证明及性质【例4】如图，已知点D 为等腰Rt △ABC 内一点，∠CAD ＝∠CBD＝15°，E 为AD 延长线上的一点，且CE ＝CA.若点M 在DE 上，且DC ＝DM ，试探究线段ME 与BD 的数量关系，并说明理由．【解析】连接MC ，先证△BDC≌△ADC，再证△ADC≌△EMC.【学生解答】解：如图，连接MC ，在等腰Rt △ABC 中，∵∠CAD ＝∠CBD＝15°，∴∠BAD ＝∠ABD＝45°－15°＝30°，∴BD ＝AD ，又AC ＝BC ，∴△BDC ≌△ADC(SSS )，∴∠DCA ＝∠DCB＝45°，∠EDC ＝∠DAC＋∠DCA＝15°＋45°＝60°.∵DC ＝DM ，∴△MDC 是等边三角形，即CM ＝CD ，又∵∠EMC＝180°－∠DMC＝180°－60°＝120°，∠ADC ＝180°－∠MDC＝180°－60°＝120°，∴∠EMC ＝∠ADC.又∵CE＝CA ，∴∠DAC ＝∠CEM＝15°，∴△ADC ≌△EMC(AAS )，∴ME ＝AD ＝DB ，∴ME ＝BD.4．(2016南京中考)如图，四边形ABCD 的对角线AC 、BD 相交于点O ，△ABO ≌△ADO ，下列结论：①AC⊥BD；②CB＝CD ；③△ABC≌△ADC；④DA＝DC ，其中正确结论的序号是__①②③__．图形旋转中全等三角形的判定与性质【例5】(2015苏州中考)如图，在Rt △ABC 中，∠ACB ＝90°，点D ，F 分别在AB ，AC 上，CF ＝CB ，连接CD ，将线段CD 绕点C 按顺时针方向旋转90°后得CE ，连接EF.(1)求证：△BCD≌△FCE；(2)若EF∥CD，求∠BDC 的度数．【解析】(1)由旋转的性质可得：CD ＝CE ，再根据同角的余角相等可证明∠BCD＝∠FCE，再根据全等三角形的判定方法即可证明△BCD≌△FCE.(2)由(1)可知△BCD≌△FCE，所以∠BDC＝∠E，易求∠E＝90°，进而可求出∠BDC 的度数．【学生解答】解：(1)∵将线段CD 绕点C 按顺时针方向旋转90°后得CE ，∴CD ＝CE ，∠DCE ＝90°，又∵∠ACB ＝90°，∴∠BCD ＝90°－∠ACD＝∠FCE，在△BCD 和△FCE 中，⎩⎪⎨⎪⎧CB ＝CF ，∠BCD ＝∠FCE，CD ＝CE ，∴△BCD ≌△FCE(SAS )；(2)由(1)可知△BCD≌△FCE，∴∠BDC ＝∠E，∵EF ∥CD ，∴∠E ＝180°－∠DCE＝90°，∴∠BDC ＝90°.5．(2016怀化三模)如图，在Rt △ABC 中，∠ABC ＝90°，点D 在边AB 上，使DB ＝BC ，过点D 作EF⊥AC，分别交AC 于点E ，交CB 的延长线于点F.求证：AB ＝BF.提示：证Rt △ABC ≌Rt △FBD 即可．6．(2016淄博中考)如图，已知△ABC，AD 平分∠BAC 交BC 于点D ，BC 的中点为M ，ME ∥AD ，交BA 的延长线于点E ，交AC 于点F.求证：(1)AE ＝AF ；(2)BE ＝12(AB ＋AC)．证明：(1)∵AD 平分∠BAC，∴∠BAD ＝∠CAD.∵AD∥EM，∴∠BAD ＝∠AEF，∠CAD ＝∠AFE，∴∠AEF ＝∠AFE，∴AE ＝AF ；(2)过点C 作CG∥EM，交BA 的延长线于点G ，∴∠AGC ＝∠AEF，∠ACG ＝∠AFE.∵∠AEF＝∠AFE，∴∠AGC ＝∠ACG，∴AG ＝AC.∵BM＝CM ，EM ∥CG ，∴BE ＝EG ，∴BE ＝12BG ＝12(BA ＋AG)＝12(AB ＋AC)．。

第四章图形的初步认识与三角形、四边形第一节线段、角、相交线和平行线1．(2016汇川中考五模)如图，∠1的内错角是( D)A．∠2 B．∠3 C．∠4 D．∠5(第1题图)(第2题图)2．(2016百色中考)如图，直线a，b被直线c所截，下列条件能使a∥b的是( B)A．∠1＝∠6 B．∠2＝∠6C．∠1＝∠3 D．∠5＝∠73．(2016黄冈中考)如图，直线a∥b，∠1＝55°，则∠2＝( C)A．35°B．45°C．55°D．65°(第3题图)(第4题图)4．(2016东营中考)如图，直线m∥n，∠1＝70°，∠2＝30°，则∠A等于( C)A．30°B．35°C．40°D．50°5．(2016襄阳中考)如图，AD是∠EAC的平分线，AD∥BC，∠B＝30°，则∠C的度数为( C) A．50°B．40°C．30°D．20°6．(2015福州中考)下列图形中，由∠1＝∠2能得到AB∥CD的是( B),A) ,B),C) ,D)7．(2016湘西中考)如图，直线CD∥EF，直线AB与CD，EF分别相交于点M，N，若∠1＝30°，则∠2＝__30°__．8．(2016遵义升学样卷)把一块直尺与一块三角板如图放置，若∠1＝45°，则∠2的度数为( D)A．115°B．120°C．145°D．135°(第8题图)(第9题图)9．(2016苏州中考)如图，直线a∥b，直线l与a、b分别相交于A、B两点，过点A作直线l的垂线交直线b于点C，若∠1＝58°，则∠2的度数为( C)A．58°B．42°C．32°D．28°10．(2016枣庄中考)如图，∠AOB的一边OA为平面镜，∠AOB＝37°36′，在OB上有一点E，从E点射出一束光线经OA上一点D反射，反射光线DC恰好与OB平行，则∠DEB的度数是( B)A．75°36′B．75°12′C．74°36′D．74°12′(第10题图)(第11题图)11．(2016昆明中考)如图，AB∥CE，BF交CE于点D，DE＝DF，∠F＝20°，则∠B的度数为__40°__．12．(2016宜宾中考)如图，直线a∥b，∠1＝45°，∠2＝30°，则∠P＝__75__°.(第12题图)(第13题图)13．(2016安顺中考)如图，直线m∥n，△ABC为等腰直角三角形，∠BA C＝90°，则∠1＝__45__°.。