第五章 结构位移计算习题

第5章静定结构位移计算的虚力法
5.1 复习笔记
本章重点介绍了虚力法的原理以及如何运用虚力法对不同结构在各种荷载作用下的指定位移进行求解。

遵循“化整为零、积零为整”的思想，对结构的局部位移公式进行了分项讨论，在虚力法的指导下叠加组成了结构的整体变形公式，随后将虚力法升华到了对广义单位荷载的设定以及对广义位移的求解；通过引入图乘法，结构的弯矩变形公式的求解变得更加快捷且精确；最后介绍了温度影响下结构的位移求解并归纳了线性变形体系的四个互等定理。

一、虚力法求刚体体系的位移（见表5-1-1）
表5-1-1 虚力法求刚体体系的位移
图5-1-1
二、虚力法求静定结构的位移（见表5-1-2）
表5-1-2 虚力法求静定结构的位移
表5-1-3 广义位移分类
三、两个对偶解法——虚力法求位移、虚位移法求内力（见表5-1-4）
表5-1-4 两个对偶解法——虚力法求位移、虚位移法求内力
四、荷载作用时静定结构的弹性位移计算（见表5-1-5）
表5-1-5 荷载作用时静定结构的弹性位移计算
五、图乘法（见表5-1-6）
表5-1-6 图乘法
图5-1-2 六、温度改变时静定结构位移计算（见表5-1-7）。

第5章静定结构位移计算的虚力法
5.1复习笔记
本章重点介绍了虚力法的原理以及如何运用虚力法对不同结构在各种荷载作用下的指定位移进行求解。

遵循“化整为零、积零为整”的思想，对结构的局部位移公式进行了分项讨论，在虚力法的指导下叠加组成了结构的整体变形公式，随后将虚力法升华到了对广义单位荷载的设定以及对广义位移的求解；通过引入图乘法，结构的弯矩变形公式的求解变得更加快捷且精确；最后介绍了温度影响下结构的位移求解并归纳了线性变形体系的四个互等定理。

一、虚力法求刚体体系的位移（见表5-1-1）
表5-1-1虚力法求刚体体系的位移
二、虚力法求静定结构的位移（见表5-1-2）
表5-1-2虚力法求静定结构的位移
表5-1-3广义位移分类
三、两个对偶解法——虚力法求位移、虚位移法求内力（见表5-1-4）
表5-1-4两个对偶解法——虚力法求位移、虚位移法求内力
四、荷载作用时静定结构的弹性位移计算（见表5-1-5）
表5-1-5荷载作用时静定结构的弹性位移计算。

第二章 平面体系的几何组成分析练习题：1、判断题多余约束是体系中不需要的约束。

（C ） 瞬变体系在很小的荷载作用下会产生很大的内力，所以不能作为结构使用。

（ D ） 两根链杆的约束作用相当于一个单铰。

（ C ） 每一个无铰封闭框都有三个多余约束。

（ D ） 连接四个刚片的复铰相当于四个约束。

（ C ）图示体系是由三个刚片用三个共线的铰ABC 相连，故为瞬变体系。

（ C ） 图示体系是由三个刚片用三个共线的铰ABC 相连，故为瞬变体系。

（ C ）@2、单项选择题/将三刚片组成无多余约束的几何不变体系，必要的约束数目是几个 （ D ） A 2B 3C4D 6 三刚片组成无多余约束的几何不变体系，其联结方式是（ B ）A 以任意的三个铰相联B 以不在一条线上三个铰相联C 以三对平行链杆相联D 以三个无穷远处的虚铰相联 瞬变体系在一般荷载作用下（ C ）A 产生很小的内力B 不产生内力C 产生很大的内力D 不存在静力解答@题图从一个无多余约束的几何不变体系上去除二元体后得到的新体系是 （ A ）A 无多余约束的几何不变体系B 有多余约束的几何不变体系 ，C 几何可变体系D 几何瞬变体系图示体系属于（ A ）A 静定结构B 超静定结构C 常变体系D 瞬变体系图示体系属于（C ）*A无多余约束的几何不变体系 B 有多余约束的几何不变体系C 有多余约束的几何可变体系D 瞬变体系 不能作为建筑结构使用的是（ D ）A 无多余约束的几何不变体系B 有多余约束的几何不变体系C 几何不变体系D 几何可变体系 一根链杆（ D ） A 可减少两个自由度 B 有一个自由度C 有两个自由度D 可减少一个自由度图示体系是（ D ）A瞬变体系B有一个自由度和一个多余约束的可变体系%C 无多余约束的几何不变体系`图示体系是（B ）A 瞬变体系B 有一个自由度和一个多余约束的可变体系C 无多余约束的几何不变体系D 有两个多余约束的几何不变体系下列那个体系中的1点不是二元体（ C ）\题图题图 题图题图…对图示体系进行几何组成分析。

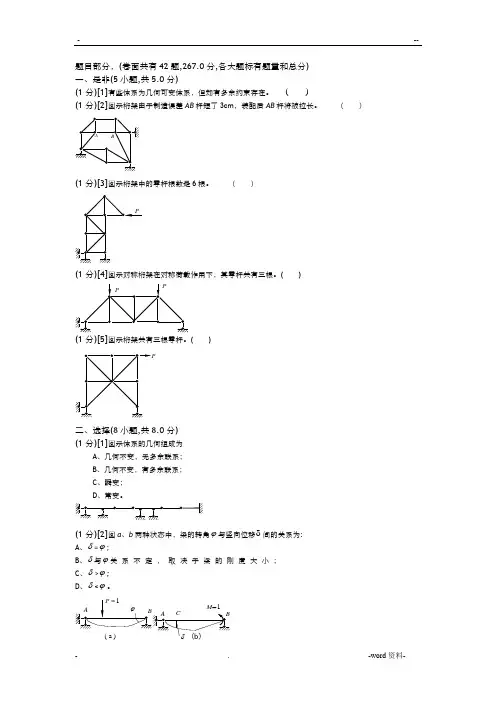
题目部分，(卷面共有42题,267.0分,各大题标有题量和总分)一、是非(5小题,共5.0分)(1分)[1]有些体系为几何可变体系，但却有多余约束存在。

()(1分)[2]图示桁架由于制造误差AB杆短了3cm，装配后AB杆将被拉长。

（）A B(1分)[3]图示桁架中的零杆根数是6根。

（）(1分)[4]图示对称桁架在对称荷载作用下，其零杆共有三根。

( )(1分)[5]图示桁架共有三根零杆。

( )二、选择(8小题,共8.0分)(1分)[1]图示体系的几何组成为A、几何不变，无多余联系；B、几何不变，有多余联系；C、瞬变；D、常变。

(1分)[2]图a、b两种状态中，粱的转角ϕ与竖向位移δ间的关系为:A、δ=ϕ;B、δ与ϕ关系不定，取决于梁的刚度大小；C、δ>ϕ;D、δ<ϕ。

(1分)[3]图示结构的弯矩图中，B点的弯矩是：A、使外侧受拉；B、使内侧受拉；C、为零；D、以上三种可能都存在。

m(1分)[4]图示结构B点杆端弯矩（设内侧受拉为正）为：A、MBA=Pa,M BC=－Pa；B、MBA=M BC=2Pa；C、MBA=M BC=Pa；D、M =M=0。

a aa(1分)[5]图示平面体系的几何组成性质是：A、几何不变,且无多余联系；B、几何不变,且有多余联系；C、几何可变；D、瞬变。

(1分)[6]图示桁架杆a的内力为：A、-55kN;B、15kN;C、-15kN;D、0。

3mm4m 3m(1图示简支斜梁，在荷载P作用下，若改变B支座链杆方向，则梁的内力将是：A、M、Q、N都改变；B、M、N不变，Q改变，C、M、Q不变，N改变；D、M不变，Q、N改变。

(1分)[8]图示刚架杆端弯矩M BC 为：A 、80kN m ⋅（下侧受拉）；B 、40kN m ⋅（下侧受拉）；C 、80kN m ⋅(上侧受拉）；D 、40kN m ⋅(上侧受拉）。

20kN/m4m三、填充(5小题,共6.0分)(2分)[1]图示体系的几何组成分析的结论是 。

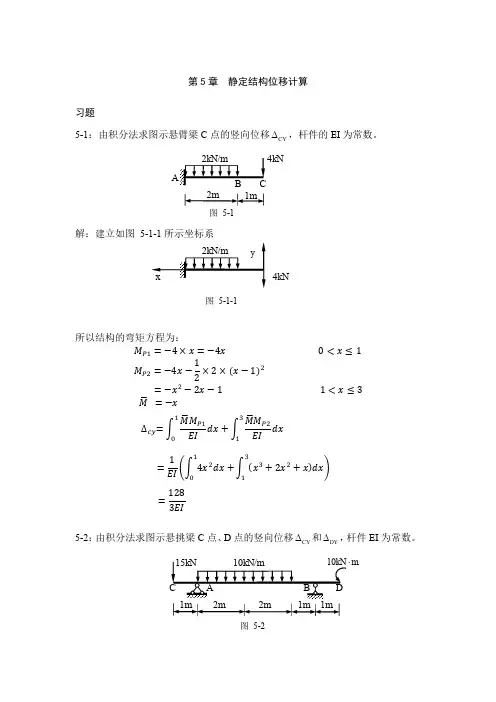
第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;;B.D.M C.=1=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M kM p21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

aa9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。

二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。

qlll /211、求图示静定梁D 端的竖向位移 ∆DV 。

EI = 常数 ，a = 2m 。

a a a10kN/m12、求图示结构E 点的竖向位移。

EI = 常数 。

ll l l /32 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。

求D 点的竖向位移。

P 3m3m3m14、求图示刚架B 端的竖向位移。

q15、求图示刚架结点C 的转角和水平位移，EI = 常数 。

q16、求图示刚架中Ｄ点的竖向位移。

EI ＝ 常数 。

l/217、求图示刚架横梁中Ｄ点的竖向位移。

EI ＝ 常数 。

18、求图示刚架中D 点的竖向位移。

E I = 常数 。

qll/219、求图示结构Ａ、Ｂ两截面的相对转角，EI ＝ 常数 。

l/23l/320、求图示结构A 、B 两点的相对水平位移，E I = 常数。

ll21、求图示结构B 点的竖向位移，EI = 常数。

5-1 试回答：用单位荷载法计算结构位移时有何前提条件？单位荷载法是否可用于超静定结构的位移计算？aaaaa NCD NCE NBE NAD NBC NAC DE F F 0, F F F F F A B P P P PR R F F F =========-由对称性分析知道N NP 12()F F 1()2 6.832222()P P P cx P F a l F a F a EA EA EA EA EA ⨯⨯-⨯-⨯∆==⨯+⨯+=↓∑5-4 已知桁架各杆截面相同，横截面面积A ＝30cm 2，E ＝20.6×106N/cm 2，F P ＝98.1kN 。

试求C 点竖向位移yC Δ。

25544P P P P F F F ===NAD NAE NEC NEF 由节点法知：对A 节点 F F 对E 节点 F F115(122516(()4)4 11.46 ()N NP yc P P P F F l F F EA EA cm =∆==⨯⨯⨯+⨯⨯+⨯⨯=↓∑NAD NAE 由节点法知：对A 节点 F F5-5 已知桁架各杆的EA 相同，求AB 、BC 两杆之间的相对转角B Δθ。

杆的内力计算如图所示施加单位力在静定结构上。

其受力如图11(12N NP BF F l EA EAθ∆==-∑5-6 试用积分法计算图示结构的位移：（a ）yB Δ；（b ）yC Δ；（c ）B θ；（d ）xB Δ。

(a)211232113421yc 1004142B ()1()26()111 ()()()26111 =()30120p llp q q q x x q l q qM x q x x lM x x q q M x M x dx q x x dx EI EI l q l q l EI -=+-=+=-∴∆=⨯=++⎰⎰以点为原点，向左为正方向建立坐标。

显然，A Bq 2q 1lEI22q l 254q l PM l74l M2224113153251315127()()324244342243416yc ql q l l ql l ql l l l l l ql EI EI ∆=⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=↓(c)22201()(sin )12(1cos )2()1111[(sin )12(1cos)]2(8-3)-1.42=()EI EIB M R R M R R Rd EIπϕϕϕϕθϕϕϕπ=⨯-⨯-==⨯⨯-⨯-=⎰逆时针l3l 4ABCql EI=常数OAB1kN/m2kNR =2m4mϕθqds qRd θ=20()sin()(1cos )M qRd R qR ϕϕθϕθϕ=⨯-=-⎰2240()sin 111()()(1cos )sin ()2xBM R M M ds qR R Rd qR EI EI EIπϕϕϕϕϕϕϕ=∆==-=←⎰⎰5-7 试用图乘法计算图示梁和刚架的位移：（a ）yC Δ；（b ）yD Δ；（c ）xC Δ；（d ）xE Δ；（e ）D θ；（f ）yE Δ。